V článcích 2.2 a 2.3 jsme užívali (viz rovnice
(2,5)
)
pro vyjádření gravitačního působení na hmotný bod hmotnosti m
sílu tvaru (v rovnici
(2,5)
byla označena
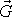 )
)
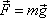 , , |
(4,8) |
kde vektor tíhového zrychlení
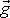 byl pokládán za konstantní vektor. Jak
souvisí silové pole
(4,8)
se silovým polem
(4,3)
? Přijmeme bez důkazu (viz
např. [20], kap.5; [5], [8]) tvrzení, že gravitační pole vně Země lze popsat
výrazem
(4,3)
, položíme-li počátek soustavy souřadnic, tj. bod o polohovém
vektoru
byl pokládán za konstantní vektor. Jak
souvisí silové pole
(4,8)
se silovým polem
(4,3)
? Přijmeme bez důkazu (viz
např. [20], kap.5; [5], [8]) tvrzení, že gravitační pole vně Země lze popsat
výrazem
(4,3)
, položíme-li počátek soustavy souřadnic, tj. bod o polohovém
vektoru
 , do středu Země. V blízkosti Země pak můžeme pokládat výraz
, do středu Země. V blízkosti Země pak můžeme pokládat výraz
 za přibližně stálý a rovný
za přibližně stálý a rovný
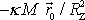 , kde
, kde
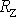 je označen poloměr Země a
je označen poloměr Země a
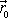 jednotkový vektor v radiálním směru,
tedy jednotkový vektor orientovaný svisle vzhůru. Síla
jednotkový vektor v radiálním směru,
tedy jednotkový vektor orientovaný svisle vzhůru. Síla
 působící na hmotný bod o hmotnosti m
v blízkosti Země je pak již shodná se
silou
(4,8)
, položíme-li
působící na hmotný bod o hmotnosti m
v blízkosti Země je pak již shodná se
silou
(4,8)
, položíme-li
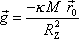 , , |
(4,9) |
jak plyne z rovnosti
 . Pro velikost
. Pro velikost
 tíhového zrychlení z rovnice
(4,9)
dostáváme
tíhového zrychlení z rovnice
(4,9)
dostáváme
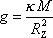 . . |
(4,10) |
Jednoduché vyjádření gravitačního pole tvarem
(4,8)
lze
provést jen pro tak velký prostor u povrchu Země, kde je možné zanedbat
změnu velikosti výrazu
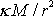 s výškou
s výškou
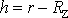 nad povrchem Země a vzájemný úhel svislic
v jednotlivých místech uvažovaného prostoru. Pole popsané rovnicí
(4,8)
nazýváme tíhovým polem.
nad povrchem Země a vzájemný úhel svislic
v jednotlivých místech uvažovaného prostoru. Pole popsané rovnicí
(4,8)
nazýváme tíhovým polem.
Práce vykonaná v tíhovém poli (4,8) na hmotný bod, přejde-li z místa C do místa D,
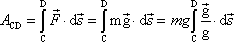 . . |
Výraz
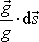 je průmět elementu dráhy
je průmět elementu dráhy
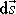 do směru tíhového zrychlení
do směru tíhového zrychlení
 . Proložíme-li směrem
. Proložíme-li směrem
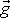 , tj. svislým směrem, souřadnicou osu
, tj. svislým směrem, souřadnicou osu
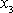 orientovanou proti smyslu
orientovanou proti smyslu
 , dostáváme
, dostáváme
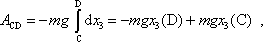 |
kde
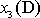 je
je
 souřadnice bodu D a analogický význam má
symbol
souřadnice bodu D a analogický význam má
symbol
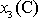 . Na ostatních kartézských souřadnicích, které lze volit libovolně v rovině
kolmé k ose
. Na ostatních kartézských souřadnicích, které lze volit libovolně v rovině
kolmé k ose
 , práce
, práce
 zřejmě nezávisí. Tíhové pole je
konzervativní, neboť práce
zřejmě nezávisí. Tíhové pole je
konzervativní, neboť práce
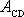 nezávisí na tvaru cesty z bodu C do
bodu D. Rozdíl potenciální energie mezi body D a C je dle rovnice
(3,14)
, po
dosazení vypočtené hodnoty práce
nezávisí na tvaru cesty z bodu C do
bodu D. Rozdíl potenciální energie mezi body D a C je dle rovnice
(3,14)
, po
dosazení vypočtené hodnoty práce
 ,
,
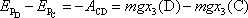 . . |
(4,11) |
Rozdíl potenciální energie je dán výškovou odlehlostí bodů.
V tíhovém poli zpravidla volíme dosud neurčenou konstantu potenciální
energie tak, že pro bod, který má souřadnici
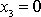 , položíme potenciální energii rovnu nule. Předpokládáme-li, že bodem o
souřadnici
, položíme potenciální energii rovnu nule. Předpokládáme-li, že bodem o
souřadnici
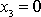 je bod C z rovnice
(4,11)
,
je bod C z rovnice
(4,11)
,
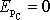 a pro potenciální energii
a pro potenciální energii
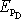 bodu D dostáváme vyjádření
bodu D dostáváme vyjádření
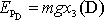 . Bod D lze volit libovolně, jeho označení je nepodstatné a pro potenciální energii
tíhového pole
. Bod D lze volit libovolně, jeho označení je nepodstatné a pro potenciální energii
tíhového pole
 při dané volbě konstanty můžeme psát
při dané volbě konstanty můžeme psát
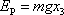 . . |
(4,12) |
Pro jinou volbu nulové hladiny potenciální energie lze místo výrazu (4,12) psát
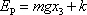 |
(4,12´) |
kde k
je zatím neurčená konstanta. Zvolíme-li nulovou hladinu potenciální
energie na povrchu Země a h
označíme výšku nad povrchem Země, dostaneme pro potenciální energii
tíhového pole známé (viz [1]) vyjádření
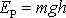 . Potenciál tíhového pole
(4,12)
je
. Potenciál tíhového pole
(4,12)
je
 a intenzita pole
a intenzita pole
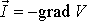 má jedinou nenulovou složku
má jedinou nenulovou složku
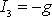 .
.
V článku 2.3 je odvozeno, že volný hmotný bod se v tíhovém poli pohybuje po trajektorii dané rovnicemi (2,9) ; koná tedy některý z vrhů. Pro šikmý vrh hmotného bodu o hmotnosti m vypočteme veličiny zavedené v kapitole 3 a ověříme jejich vzájemné vztahy.
Budeme vyšetřovat šikmý vrh, který v souřadnicové soustavě užité v rovnicích (2,9) je určen parametrickými rovnicemi
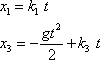 . . |
(4,13) |
Je to šikmý vrh v rovině kolmé k
 . Hmotný bod v čase
. Hmotný bod v čase
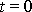 se nachází v počátku soustavy
souřadnic. Z rovnic
(4,13)
dostáváme pro rychlost hmotného bodu vyjádření
se nachází v počátku soustavy
souřadnic. Z rovnic
(4,13)
dostáváme pro rychlost hmotného bodu vyjádření
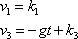 . . |
(4,14) |
Vypočteme nejprve práci A
, kterou vykoná tíhové pole
na hmotný bod o hmotnosti m
, přejde-li bod z počátečního bodu
O do libovolného bodu na trajektorii, který označíme B (viz obr.15).
K výpočtu práce užijeme rovnici
(3,6)
, kde čas
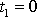 , jelikož v bodě O se hmotný bod nachází v čase
, jelikož v bodě O se hmotný bod nachází v čase
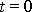 , a čas
, a čas
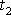 , kdy se hmotný bod nachází v bodě B označíme T.
, kdy se hmotný bod nachází v bodě B označíme T.
Dostaneme
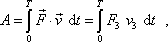 |
protože síla
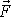 má nenulovou pouze třetí složku
má nenulovou pouze třetí složku
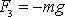 . Po dosazení za
. Po dosazení za
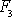 a
a
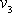
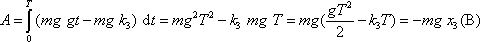 . . |
(4,15) |
Práce A je tedy rovna
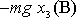 , neboť
, neboť
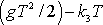 je dle
(4,13)
zřejmě třetí souřadnice
je dle
(4,13)
zřejmě třetí souřadnice
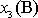 bodu B. Výraz
bodu B. Výraz
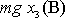 je rozdíl potenciální energie tíhového pole
mezi body B a O, protože
je rozdíl potenciální energie tíhového pole
mezi body B a O, protože
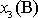 je výšková odlehlost těchto dvou bodů.
Dostáváme tak očekávaný výsledek, že práce A
vykonaná vnějšími silami na hmotný bod je rovna záporně vzatému
přírůstku potenciální energie hmotného bodu
je výšková odlehlost těchto dvou bodů.
Dostáváme tak očekávaný výsledek, že práce A
vykonaná vnějšími silami na hmotný bod je rovna záporně vzatému
přírůstku potenciální energie hmotného bodu
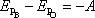 . . |
(4,16) |
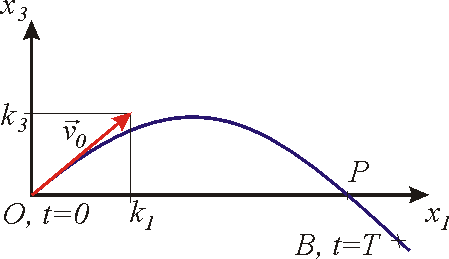 Předpokládáme ve shodě s obr.15, že
Předpokládáme ve shodě s obr.15, že
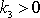 . Pro body, pro které
. Pro body, pro které
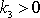 , tj. pro body, do kterých hmotný bod dojde dříve než do bodu P vyzna-čeného na
obr.15, je práce
, tj. pro body, do kterých hmotný bod dojde dříve než do bodu P vyzna-čeného na
obr.15, je práce
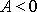 . Složka počáteční rychlosti
. Složka počáteční rychlosti
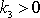 mířící proti směru tíhového pole způsobí, že
v první fázi pohybu práce vykonaná na hmotný bod tíhovými sila-mi je
záporná a hmotný bod prochází místy pole, ve kterých je potenciální energie
vyšší než v počátečním bodě O pohybu.
mířící proti směru tíhového pole způsobí, že
v první fázi pohybu práce vykonaná na hmotný bod tíhovými sila-mi je
záporná a hmotný bod prochází místy pole, ve kterých je potenciální energie
vyšší než v počátečním bodě O pohybu.
Zjistíme nyní přímým výpočtem rozdíl
 kinetických energií hmotného bodu
v bodě B a v bodě O. V bodě O je kinetická energie
kinetických energií hmotného bodu
v bodě B a v bodě O. V bodě O je kinetická energie
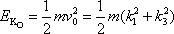 , , |
kde hodnotu velikosti rychlosti
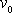 v bodě O získáme běžným postupem
z rovnic
(4,14)
, kam dosadíme
v bodě O získáme běžným postupem
z rovnic
(4,14)
, kam dosadíme
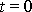 . Velikost rychlosti
. Velikost rychlosti
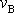 v bodě B, tj. v čase T
, získáme obdobně z rovnic
(4,14)
, položíme-li
v bodě B, tj. v čase T
, získáme obdobně z rovnic
(4,14)
, položíme-li
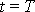 .
.
V bodě B je kinetická energie
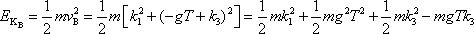 . . |
Rozdíl
 . Poslední výraz je však dle
(4,15)
roven práci A
vykonané na hmotný bod tíhovým polem, přejde-li z bodu O do
bodu B, tedy
. Poslední výraz je však dle
(4,15)
roven práci A
vykonané na hmotný bod tíhovým polem, přejde-li z bodu O do
bodu B, tedy
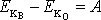 . Pro šikmý vrh jsme tak přímým výpočtem získali rovnici
(3,11)
. Porovnáním
poslední rovnice s rovnicí
(4,16)
dostáváme po snadné úpravě
. Pro šikmý vrh jsme tak přímým výpočtem získali rovnici
(3,11)
. Porovnáním
poslední rovnice s rovnicí
(4,16)
dostáváme po snadné úpravě
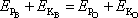 , , |
(4,17) |
tj. zákon zachování mechanické energie při pohybu hmotného bodu po trajektorii
(4,13)
.
Z rovnice
(4,17)
lze získat velikosti rychlosti hmotného bodu
v každém bodě B trajektorie, aniž ji musíme přímo počítat z rovnice
(4,14)
. Zvolíme, jak je obvyklé,
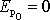 , pak z
(4,17)
plyne
, pak z
(4,17)
plyne
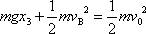 . . |
a tedy
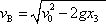 . . |
(4,18) |
Z rovnice
(4,18)
dostáváme
 pro body nad osou
pro body nad osou
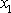 , pro bod P vyznačený na obr.15, který má
, pro bod P vyznačený na obr.15, který má
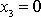 , dostáváme
, dostáváme
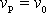 a
a
 pro body pod osou
pro body pod osou
 . V případě
. V případě
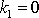 , tj. při vrhu svislém vzhůru, bod B má ve vrcholu nulovou velikost
rychlosti
, tj. při vrhu svislém vzhůru, bod B má ve vrcholu nulovou velikost
rychlosti
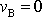 . Z rovnice
(4,18)
pak pro výšku vrhu
. Z rovnice
(4,18)
pak pro výšku vrhu
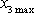 dostáváme podmínku
dostáváme podmínku
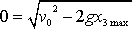 , z které plyne
, z které plyne
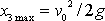 .
.
Dále ověříme pro vyšetřovaný šikmý vrh platnost rovnice
(3,8)
. Výkon P
je definován rovnicí
(3,7)
jako
 . Rovnicí
(4,15)
máme práci A
vyjádřenu jako funkci času T
, kdy se hmotný bod nachází v bodě
B. Polohu bodu B pokládáme za proměnnou a symbol pro čas označíme
t místo T, potom
. Rovnicí
(4,15)
máme práci A
vyjádřenu jako funkci času T
, kdy se hmotný bod nachází v bodě
B. Polohu bodu B pokládáme za proměnnou a symbol pro čas označíme
t místo T, potom
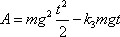 |
a výkon
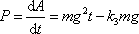 . . |
Vypočteme výraz
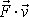 , který dle rovnice
(3,8)
se má rovnat výkonu P
. Jelikož síla
, který dle rovnice
(3,8)
se má rovnat výkonu P
. Jelikož síla
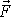 má jedinou nenulovou složku
má jedinou nenulovou složku
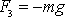 a dle
(4,14)
a dle
(4,14)
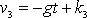 , dostáváme
, dostáváme
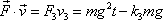 , , |
což je opravdu výraz shodný s výrazem pro výkon P. Okamžitý výkon tíhové síly konaný na vyšetřovaný hmotný bod lze vyjádřit jako skalární součin síly (okamžité zde není třeba zdůrazňovat) a okamžité rychlosti bodu.
Vztahy
(3,28)
mezi impulsem a hybností a
(3,36)
mezi
momentem hybnosti a momentem síly lze též dobře demonstrovat na vyšetřovaném
příkladě. Impuls
 síly
síly
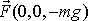 v časovém intervalu
v časovém intervalu
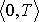 stanovíme dle definiční rovnice
(3,27)
stanovíme dle definiční rovnice
(3,27)
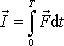 . Dostaneme
. Dostaneme
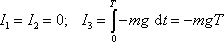 . . |
(4,19) |
Hybnost
 hmotného bodu v místě O je dána
vektorem
hmotného bodu v místě O je dána
vektorem
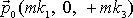 , hybnost hmotného bodu v čase T je dána vektorem
, hybnost hmotného bodu v čase T je dána vektorem
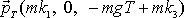 , jak lze zjistit dosazením rychlosti
, jak lze zjistit dosazením rychlosti
 z rovnic
(4,14)
. Změna hybnosti
hmotného bodu, tj. rozdíl hybností
z rovnic
(4,14)
. Změna hybnosti
hmotného bodu, tj. rozdíl hybností
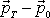 , je vektor o složkách
, je vektor o složkách
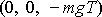 , tedy vektor totožný s vektorem impulsu
, tedy vektor totožný s vektorem impulsu
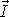 , jehož složky jsou dány rovnicemi
(4,19)
, což odpovídá ověřované rovnici
(3,28)
.
, jehož složky jsou dány rovnicemi
(4,19)
, což odpovídá ověřované rovnici
(3,28)
.
Moment hybnosti
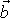 hmotného m vzhledem k počátku soustavy souřadnic je dán výrazem
(3,35)
hmotného m vzhledem k počátku soustavy souřadnic je dán výrazem
(3,35)
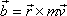 . . |
(3,35) |
Polohový vektor
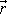 je vektor o složkách rovných souřadnicím
hmotného bodu, tedy dle rovnic
(4,13)
je
je vektor o složkách rovných souřadnicím
hmotného bodu, tedy dle rovnic
(4,13)
je
 . Složky vektoru
. Složky vektoru
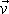 jsou dány rovnicemi
(4,14)
. Vypočteme-li
s takto zadanými vektory
jsou dány rovnicemi
(4,14)
. Vypočteme-li
s takto zadanými vektory
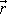 a
a
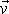 vektorový součin
(3,35)
, zjistíme, že
vektor
vektorový součin
(3,35)
, zjistíme, že
vektor
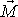 má jedinou nenulovou složku
má jedinou nenulovou složku
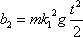 . . |
(4,20) |
Moment síly vůči počátku soustavy souřadnic je dle
(3,32)
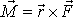 . Moment síly působící na vyšetřovaný hmotný bod v čase t
dostaneme vektorovým vynásobením
vektoru
. Moment síly působící na vyšetřovaný hmotný bod v čase t
dostaneme vektorovým vynásobením
vektoru
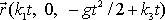 vektorem
vektorem
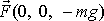 . Zjistíme, že vektor
. Zjistíme, že vektor
 má jedinou nenulovou složku
má jedinou nenulovou složku
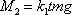 . . |
(4,21) |
Kladná znaménka na pravých stranách rovnic (4,20) a (4,21) jsou podmíněně předpokladem, že užíváme pravotočivou soustavu souřadnic. Zderivujeme-li rovnici (4,20) dle času t, dostaneme
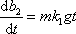 . . |
Pravá strana poslední rovnice je
totožná s pravou stranou rovnice
(4,21)
, tedy
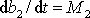 . Vzhledem k nulovým hodnotám ostatních složek vektorů
. Vzhledem k nulovým hodnotám ostatních složek vektorů
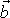 a
a
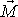 jsou rovnice
jsou rovnice
 pro
pro
 splněny triviálně. Přímým výpočtem jsme
získali rovnici
splněny triviálně. Přímým výpočtem jsme
získali rovnici
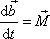 , , |
která souhlasí s obecnou rovnicí (3,36) .
Při šikmém vrhu na hmotný bod působí pouze tíhové síly. Hmotný bod není podroben žádným vazbám, říkáme, že je volný . Zákon zachování energie (4,17) platí i pro pohyby hmotných bodů, na které v konzervativním silovém poli působí vazby takového druhu, že vazbové síly nekonají na hmotný bod práci. Nejznámějšími takovými pohyby v tíhovém poli jsou pohyb bez tření po nakloněné rovině a pohyb matematického kyvadla. Vazbové síly udržující hmotný bod na nakloněné rovině a vazbové síly udržující hmotný bod matematického kyvadla v pevné vzdálenosti od bodu závěsu jsou kolmé ke směru pohybu, a proto nekonají práci.
Vyjdeme-li ze zákona zachování energie
(4,17)
v tíhovém
poli, můžeme snadno určit velikost rychlosti
 , kterou hmotný bod o hmotnosti m
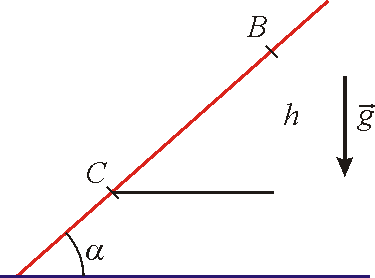
volně vypuštěný z bodu B na nakloněné rovině získá v bodě C
této roviny (viz obr.16). Energie kinetická v bodě B je
, kterou hmotný bod o hmotnosti m
volně vypuštěný z bodu B na nakloněné rovině získá v bodě C
této roviny (viz obr.16). Energie kinetická v bodě B je
 a
a
 energie potenciální
energie potenciální
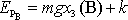 (užíváme soustavu souřadnic se svislou osou
(užíváme soustavu souřadnic se svislou osou
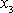 , směr tíže je na obr.16 vyznačen). V bodě C je energie kinetická
, směr tíže je na obr.16 vyznačen). V bodě C je energie kinetická
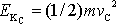 a energie potenciální
a energie potenciální
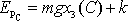 . Z rovnice
(4,17)
plyne
. Z rovnice
(4,17)
plyne
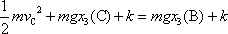 . . |
(4,22) |
Odtud pro hledanou velikost rychlosti dostaneme
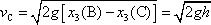 . . |
(4,23) |
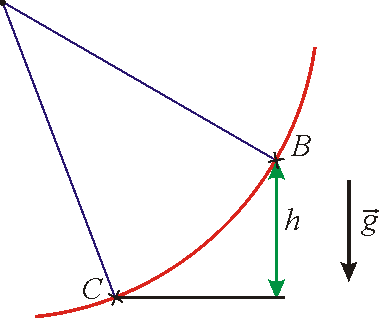 V posledním
výraze je symbolem h označena výšková
odlehlost bodů B a C. Rychlost
(4,23)
je stejná, jakou by nabyl hmotný bod
vypuštěný nulovou počáteční rychlostí volným pádem z výše h
při dopadu na zem nebo jakou by nabyl
v místě C hmotný bod vázaný vazbou matematického kyvadla vypuštěný nulovou
počáteční rychlostí z bodu B v případě, že výšková odlehlost míst B a
C je h (viz obr.17).
V posledním
výraze je symbolem h označena výšková
odlehlost bodů B a C. Rychlost
(4,23)
je stejná, jakou by nabyl hmotný bod
vypuštěný nulovou počáteční rychlostí volným pádem z výše h
při dopadu na zem nebo jakou by nabyl
v místě C hmotný bod vázaný vazbou matematického kyvadla vypuštěný nulovou
počáteční rychlostí z bodu B v případě, že výšková odlehlost míst B a
C je h (viz obr.17).
V rovnici (4,22) není totiž nijak zachycena specifičnost pohybu po nakloněné rovině. Vypočtená velikost rychlosti (4,23) závisí pouze na výškové odlehlosti bodů B a C a není podstatné, jakou cestu hmotný bod v tíhovém poli mezi body B a C vykonal.
 Je-li např. hmotný bod
nucen pohybovat se po dráze naznačené na obr.18, znovu jeho rychlost
v bodě C bude rovna
Je-li např. hmotný bod
nucen pohybovat se po dráze naznačené na obr.18, znovu jeho rychlost
v bodě C bude rovna
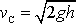 , když byl vypuštěn z bodu B nulovou počáteční rychlostí. V tomto
případě do-spěje hmotný bod do bodu D, který se nachází v tíhovém poli ve
stejné výšce jako bod B, vrátí se do bodu B a pohyb se bude stále opakovat.
Uvažujeme totiž ide-alizovaný případ, kdy nepůsobí disipativní sily (síly
tření).
, když byl vypuštěn z bodu B nulovou počáteční rychlostí. V tomto
případě do-spěje hmotný bod do bodu D, který se nachází v tíhovém poli ve
stejné výšce jako bod B, vrátí se do bodu B a pohyb se bude stále opakovat.
Uvažujeme totiž ide-alizovaný případ, kdy nepůsobí disipativní sily (síly
tření).
Celková mechanická energie hmotného bodu v místě B je rovna mgh;
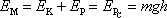 , , |
když nulovou hladinu potenciální energie položíme do bodu C.
Celková mechanická energie
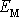 se při pohybu zachovává. Pro body výše
položené, než je bod D, by samotná potenciální energie byla vyšší, než je
celková energie hmotného bodu. To je však nemožné, protože kinetická
energie
se při pohybu zachovává. Pro body výše
položené, než je bod D, by samotná potenciální energie byla vyšší, než je
celková energie hmotného bodu. To je však nemožné, protože kinetická
energie
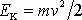 je veličina nezáporná. Chceme-li, aby hmotný
bod se dostal do bodu K naznačeného na obr.18, musíme mu v bodě B udělit
rychlost
je veličina nezáporná. Chceme-li, aby hmotný
bod se dostal do bodu K naznačeného na obr.18, musíme mu v bodě B udělit
rychlost
 takovou, aby celková energie hmotného bodu
v bodě B byla nejméně rovna potenciální energii hmotného bodu v bodě
K. Z rovnice
(4,17)
tak pro rychlost
takovou, aby celková energie hmotného bodu
v bodě B byla nejméně rovna potenciální energii hmotného bodu v bodě
K. Z rovnice
(4,17)
tak pro rychlost
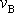 dostáváme podmínku
dostáváme podmínku
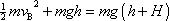 , , |
tedy
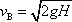 . . |
Nezáleží na tom, kterým směrem tuto rychlost hmotného bodu
v bodě B udělíme. Udělíme-li mu rychlost
 , bude se hmotný bod pohybovat přes obě minima dráhy naznačené na obr.18 až do
výšky
, bude se hmotný bod pohybovat přes obě minima dráhy naznačené na obr.18 až do
výšky
 , určené konkrétní hodnotou
, určené konkrétní hodnotou
 . Na obr.18 jsou meze pohybu v takovém případě označeny M a N.
. Na obr.18 jsou meze pohybu v takovém případě označeny M a N.