Dva hmotné body o hmotnostech
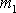 a
a
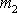 , jejichž vzdálenost je r
, působí na sebe silou, jejíž velikost je
, jejichž vzdálenost je r
, působí na sebe silou, jejíž velikost je
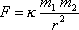 . . |
(4,1) |
Tato síla je přitažlivá a působí ve směru spojnice obou bodů.
Nachází-li se první hmotný bod v místě daném polohovým vektorem
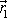 a druhý v místě daném polohovým
vektorem
a druhý v místě daném polohovým
vektorem
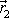 , platí pro sílu
, platí pro sílu
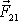 , kterou působí prvý bod na druhý, vektorové vyjádření
, kterou působí prvý bod na druhý, vektorové vyjádření
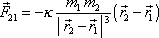 . . |
(4,2) |
Podle třetího Newtonova zákona pro sílu
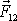 , kterou působí druhý bod na první, platí
, kterou působí druhý bod na první, platí
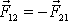 .
Právě vyslovený zákon je zákonem všeobecné gravitace.
.
Právě vyslovený zákon je zákonem všeobecné gravitace.
Keplerovy zákony, které tvořily jeden ze základních poznatků
pro vyslovení Newtonových zákonů, lze vysvětlit v jejich rámci,
předpokládáme-li, že mezi Sluncem a planetami působí gravitační síly dané
rovnicemi
(4,2)
(viz čl. 4.3). Konstantu
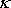 z rovnic
(4,1)
a
(4,2)
je nutno určit
experimentálně, neboť jednotky pro sílu, hmotnost a délku jsou v soustavě
jednotek SI voleny nezávisle na všeobecném gravitačním zákoně. Bývá pro ni
udávána hodnota
z rovnic
(4,1)
a
(4,2)
je nutno určit
experimentálně, neboť jednotky pro sílu, hmotnost a délku jsou v soustavě
jednotek SI voleny nezávisle na všeobecném gravitačním zákoně. Bývá pro ni
udávána hodnota
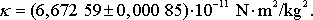
Obecně by bylo možné vycházet při budování soustavy jednotek
(viz
 ) ze všeobecného gravitačního zákona a
pokládat v něm konstantu
) ze všeobecného gravitačního zákona a
pokládat v něm konstantu
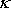 za bezrozměrový výraz o velikosti rovné
jedné. Pak by obvykle volené základní veličiny hmotnost, délka a čas nebyly
nezávislé a počet základních veličin pro mechaniku by se snížil ze tří na dvě.
Praktické zavedení zde navržené soustavy jednotek je však stěží proveditelné,
protože přesnost, s jakou jsme schopni stanovit gravitační konstantu, je
malá. V době, kdy se vytvářela nyní všeobecně uznávaná soustava SI, byla
gravitační konstanta známa pouze na tři platné číslice, tedy s relativní
přesností 10 3
, přestože se jejímu měření věnovala značná péče.
Gravitační konstantu lze totiž stanovit pouze z měření přitažlivých sil
mezi hmotnostmi, jejichž velikost jsme schopni stanovit vážením. Velikost
takových hmotností je podstatně menší než hmotnost nebeských těles a přitažlivé
síly mezi nimi jsou velmi malé. Klasická měření tohoto typu prováděli Cavendish
torzními vahami a Eőtvős kompenzační metodou modifikovanými klasickými vahami
(experimentální podrobnosti viz [5], [7]).
Jak je vidět z výše uvedené hodnoty gravitační konstanty k ,
je současně udávaná hodnota stanovena s přesností asi o řád lepší. Některá
poslední měření ukazují na další zpřesnění její hodnoty, ale přesto je taková
přesnost hluboko pod přesností, s jakou je třeba provádět měření
s veličinami, které stojí v čele prakticky použitelné soustavy
jednotek.
za bezrozměrový výraz o velikosti rovné
jedné. Pak by obvykle volené základní veličiny hmotnost, délka a čas nebyly
nezávislé a počet základních veličin pro mechaniku by se snížil ze tří na dvě.
Praktické zavedení zde navržené soustavy jednotek je však stěží proveditelné,
protože přesnost, s jakou jsme schopni stanovit gravitační konstantu, je
malá. V době, kdy se vytvářela nyní všeobecně uznávaná soustava SI, byla
gravitační konstanta známa pouze na tři platné číslice, tedy s relativní
přesností 10 3
, přestože se jejímu měření věnovala značná péče.
Gravitační konstantu lze totiž stanovit pouze z měření přitažlivých sil
mezi hmotnostmi, jejichž velikost jsme schopni stanovit vážením. Velikost
takových hmotností je podstatně menší než hmotnost nebeských těles a přitažlivé
síly mezi nimi jsou velmi malé. Klasická měření tohoto typu prováděli Cavendish
torzními vahami a Eőtvős kompenzační metodou modifikovanými klasickými vahami
(experimentální podrobnosti viz [5], [7]).
Jak je vidět z výše uvedené hodnoty gravitační konstanty k ,
je současně udávaná hodnota stanovena s přesností asi o řád lepší. Některá
poslední měření ukazují na další zpřesnění její hodnoty, ale přesto je taková
přesnost hluboko pod přesností, s jakou je třeba provádět měření
s veličinami, které stojí v čele prakticky použitelné soustavy
jednotek.
Budeme vyšetřovat gravitační silové pole, které vzniká
v okolí hmotného bodu o hmotnosti M
a pohyb hmotného bodu o hmotnosti m
v tomto silovém poli. Při tom budeme předpokládat, že
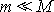 , abychom mohli položit počátek souřadné soustavy do bodu o hmotnosti
M a tuto soustavu při tom pokládat za soustavu
inerciální. Ve zvolené soustavě souřadné je totiž hmotný bod o hmotnosti
M v klidu, ale působí na něj síla od
hmotného bodu o hmotnosti m . Soustava souřadná spjatá s bodem
o hmotnosti M
není tedy inerciální.
V čl.5.6 však ukážeme, že za předpokladu
, abychom mohli položit počátek souřadné soustavy do bodu o hmotnosti
M a tuto soustavu při tom pokládat za soustavu
inerciální. Ve zvolené soustavě souřadné je totiž hmotný bod o hmotnosti
M v klidu, ale působí na něj síla od
hmotného bodu o hmotnosti m . Soustava souřadná spjatá s bodem
o hmotnosti M
není tedy inerciální.
V čl.5.6 však ukážeme, že za předpokladu
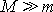 , lze soustavu souřadnou spjatou s bodem M
pokládat pro vyšetřování gravitačního působení v dobrém
přiblížení za inerciální soustavu souřadnou. Dále v citovaném článku
ukážeme, jak lze přesně řešit problém vzájemného pohybu hmotných bodů o
hmotnostech m a M
i bez předpokladu
, lze soustavu souřadnou spjatou s bodem M
pokládat pro vyšetřování gravitačního působení v dobrém
přiblížení za inerciální soustavu souřadnou. Dále v citovaném článku
ukážeme, jak lze přesně řešit problém vzájemného pohybu hmotných bodů o
hmotnostech m a M
i bez předpokladu
 . V této kapitole budeme pracovat v soustavě souřadné spjaté
s bodem o hmotnosti M
a budeme o ní předpokládat, že je inerciální.
. V této kapitole budeme pracovat v soustavě souřadné spjaté
s bodem o hmotnosti M
a budeme o ní předpokládat, že je inerciální.
Toto zjednodušení není jen početním zjednodušením, ale umožní nám učinit závěry pro celou planetární soustavu a tu již nelze jednoduše převést na řešení v inerciální soustavě. Je to problém více těles a ne jen dvou těles, který jediný je postupem uvedeným v čl.5.6 přesně řešitelný.
V soustavě souřadné s počátkem v bodě o hmotnosti
M lze gravitační sílu
(4,2)
působící na bod o hmotnosti m
, který se nachází v místě
 , zapsat ve tvaru
, zapsat ve tvaru
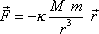 . . |
(4,3) |
Rovnicí
(4,3)
je síla
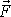 určena jako funkce souřadnic
určena jako funkce souřadnic
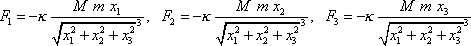 |
(4,3´) |
Síla
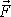 je rovnicí
(4,3)
určena pro všechny body,
jejichž polohový vektor
je rovnicí
(4,3)
určena pro všechny body,
jejichž polohový vektor
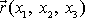 je různý od nulového vektoru, tj. pro
všechny body
je různý od nulového vektoru, tj. pro
všechny body
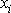 prostoru s výjimkou počátku soustavy
souřadnic, pro který všechna
prostoru s výjimkou počátku soustavy
souřadnic, pro který všechna
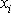 jsou současně rovna nule. Říkáme, že rovnicí
(4,3)
je zadáno gravitační silové pole
bodu o hmotnosti M
. Jeho intenzita dle definice
(3,22)
je
jsou současně rovna nule. Říkáme, že rovnicí
(4,3)
je zadáno gravitační silové pole
bodu o hmotnosti M
. Jeho intenzita dle definice
(3,22)
je
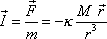 . . |
(4,4) |
Vypočteme práci
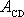 vykonanou polem
(4,3)
na hmotný bod,
přejde-li z místa C, jehož po-lohový vektor označíme
vykonanou polem
(4,3)
na hmotný bod,
přejde-li z místa C, jehož po-lohový vektor označíme
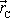 , do místa D o polohovém vektoru
, do místa D o polohovém vektoru
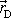 . Dle
(3,4)
je práce
. Dle
(3,4)
je práce
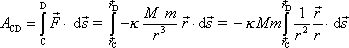 . . |
Skalární součin
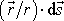 je průmětem elementu dráhy
je průmětem elementu dráhy
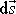 do radiálního směru, a tedy
do radiálního směru, a tedy
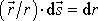 . Výraz pod integrálem se zjednoduší na tvar závislý pouze na velikosti r ,
. Výraz pod integrálem se zjednoduší na tvar závislý pouze na velikosti r ,
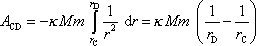 . . |
Výsledek výpočtu ukazuje, že práce
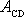 je závislá
na rozdílu vzdáleností bodů C a D od počátku soustavy souřadnic, tj. od
bodu hmotnosti M
a nezávisí na volbě cesty
z bodu C do bodu D. Z toho plyne, že gravitační silové pole bodu o
hmotnosti M
je konzervativní a lze
tedy dle rovnice
(3,14)
,
je závislá
na rozdílu vzdáleností bodů C a D od počátku soustavy souřadnic, tj. od
bodu hmotnosti M
a nezávisí na volbě cesty
z bodu C do bodu D. Z toho plyne, že gravitační silové pole bodu o
hmotnosti M
je konzervativní a lze
tedy dle rovnice
(3,14)
,
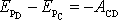 , zavést rozdíl potenciálních energií mezi libovolnými dvěma body (s výjimkou
počátku soustavy souřadnic) tohoto pole. Rozdíl je roven, dosadíme-li právě
vypočtenou hodnotu práce
, zavést rozdíl potenciálních energií mezi libovolnými dvěma body (s výjimkou
počátku soustavy souřadnic) tohoto pole. Rozdíl je roven, dosadíme-li právě
vypočtenou hodnotu práce
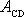 , výrazu
, výrazu
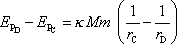 . . |
(4,5) |
Abychom získali potenciální energii jako jednoznačnou funkci
souřadnic, zvolíme její hodnotu v jednom bodě pole. Ve shodě
s obvyklou volbou položíme hodnotu potenciální energie v nekonečně
vzdáleném bodě rovnu nule. Za nekonečně vzdálený budeme v rovnici
(4,5)
pokládat např. bod D, a tedy
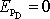 . Z rovnice
(4,5)
potom pro hodnotu potenciální energie v bodě C
dostáváme
. Z rovnice
(4,5)
potom pro hodnotu potenciální energie v bodě C
dostáváme
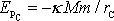 , jelikož z podmínky
, jelikož z podmínky
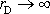 plyne
plyne
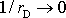 . Hodnota
. Hodnota
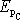 je jednoznačnou funkcí souřadnic, index C je
zbytečné dále psát a pro zavedenou standardní volbu nulové hladiny potenciální
energie budeme dále uvažovat potenciální energii gravitačního pole
bodu o hmotnosti M
jako skalární funkci souřadnic (zde pouze vzdálenosti r)
je jednoznačnou funkcí souřadnic, index C je
zbytečné dále psát a pro zavedenou standardní volbu nulové hladiny potenciální
energie budeme dále uvažovat potenciální energii gravitačního pole
bodu o hmotnosti M
jako skalární funkci souřadnic (zde pouze vzdálenosti r)
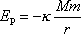 . . |
(4,6) |
Potenciál gravitačního pole bodu o hmotnosti M (viz (3,23) ) má tvar
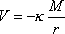 |
(4,7) |
a snadno lze ověřit i platnost vztahu (3,24) pro zde vyšetřovaný případ gravitačního pole.
Potenciální energii
(4,6)
lze, zavedeme-li kartézské
souřadnice
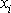 , psát ve tvaru
, psát ve tvaru
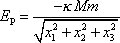 . . |
Parciální derivace
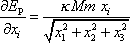 . . |
Porovnáme-li tento výsledek s rovnicemi (4,3´) , vidíme, že
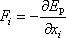 . . |
Tak jsme přímým výpočtem pro vyšetřované silové pole ověřili platnost obecné rovnice (3,21) . Ověření rovnic (3,28) by bylo zcela analogické, pouze obě strany uvažovaných rovnic by byly vyděleny hmotností m .