O nepříliš rychle proudící viskózní tekutině předpokládáme, že lne ke stěnám, kolem kterých proudí. Smykové napětí u těchto stěn není nulové, a proto tekutina na obtékané předměty působí nenulovými silami. Dalším zdrojem sil působících od tekutiny na obtékané předměty je nerovnoměrně rozložený tlak kolem těles.
Je-li Reynoldsovo číslo příslušné uvažovanému proudění malé
(řádu jednotek), převládá v odporu prostředí vliv viskózních smykových
sil. Když obtékaným předmětem je koule poloměru R, lze v tomto
případě výslednou sílu
 působící od tekutiny na kouli spočítat
(např. [1], čl. 18.8).
Velikost
působící od tekutiny na kouli spočítat
(např. [1], čl. 18.8).
Velikost
 této síly lze aproximovat výrazem
této síly lze aproximovat výrazem
kde
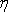 je viskozita proudící tekutiny a v velikost její rychlosti v místech, kde již
proudění není ovlivněno přítomností koule. Síla
je viskozita proudící tekutiny a v velikost její rychlosti v místech, kde již
proudění není ovlivněno přítomností koule. Síla
 má stejný směr a smysl jako rychlost
má stejný směr a smysl jako rychlost
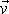 v dostatečné vzdálenosti od koule. Síla
velikosti
(4,145)
působí též na kouli pohybující se rychlostí
v dostatečné vzdálenosti od koule. Síla
velikosti
(4,145)
působí též na kouli pohybující se rychlostí
 vůči tekutině, která je v klidu.
V tomto případě je smysl síly
vůči tekutině, která je v klidu.
V tomto případě je smysl síly
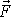 opačný, než je smysl rychlosti
opačný, než je smysl rychlosti
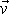 koule. Rovnice
(4,145)
se nazývá Stokesův
zákon a bývá užívána
k vystižení odporu, který tekuté prostředí klade pohybu částic, jež lze
alespoň přibližně pokládat za kulové, při proudění, kdy Reynoldsovo číslo
(4,137)
je řádu jednotek.
koule. Rovnice
(4,145)
se nazývá Stokesův
zákon a bývá užívána
k vystižení odporu, který tekuté prostředí klade pohybu částic, jež lze
alespoň přibližně pokládat za kulové, při proudění, kdy Reynoldsovo číslo
(4,137)
je řádu jednotek.
K stanovení Reynoldsova čísla dosazujeme do definiční
rovnice
(4,137)
za v vzájemnou rychlost
tekutiny a částice a za R
poloměr koule případně obdobný charakteristický rozměr částic. Stokesův
zákon tedy správně popisuje odpor prostředí vůči pohybu částic kulovitého
tvaru, když rychlost pohybu nebo rozměry částic jsou malé nebo když je velká
kinematická viskozita prostředí
 .
V takovýchto podmínkách pracuje Stokesův viskozimetr (viz např. [6], čl.
2.5.3.2), který z rychlosti pádu kuliček v kapalině určuje viskozitu
kapaliny.
.
V takovýchto podmínkách pracuje Stokesův viskozimetr (viz např. [6], čl.
2.5.3.2), který z rychlosti pádu kuliček v kapalině určuje viskozitu
kapaliny.
Odpor prostředí úměrný rychlosti částic, tj. stejnou závislost, jaká je ve Stokesově zákoně, jsme již uvažovali v I při zavedení odporující síly (4,57) . Zde je si třeba uvědomit, že výsledky získané zavedením tohoto předpokladu např. při řešení tlumených a vynucených kmitů (I, 4.5 a I, 4.6) znamenají, že výsledky tam uvedených řešení budou odpovídat realitě, jen když tlumení lze alespoň přibližně popsat Stokesovým zákonem. V případech složitějších tlumení, např. takových, jaká odpovídají dále uvedenému (4,146) Newtonovu odporovému vzorci, bude řešení tlumených a vynucených kmitů podstatně složitější. Rovnice totiž přestanou být lineárními.
Vyšetřit velikost sil působících na těleso libovolného tvaru při různě velkých vzájemných rychlostech tělesa a prostředí je složitý úkol, který velmi často je nutno řešit experimentálně.V případě, kdy hlavním zdrojem odporu prostředí nejsou viskózní síly, ale rozdíl tlaku před tělesem a za tělesem, se odpor prostředí aproximuje Newtonovým odporovým vzorcem
který bývá uváděn ve středoškolských učebnicích.
V tomto vzorci je F
velikost odporové síly, která míří ve směru rozdílu rychlosti prostředí
a rychlosti obtékaného tělesa, C je součinitel odporu,
 hustota tekutiny, S průřez vystavený
proudění, tedy kolmý ke směru vzájemné rychlosti
hustota tekutiny, S průřez vystavený
proudění, tedy kolmý ke směru vzájemné rychlosti
 prostředí a tělesa.
prostředí a tělesa.
[*] To, že rotace vektoru podobně jako vektorový součin jsou antisymetrické tenzory a ne vektory v pravém slova smyslu, působí jisté potíže, z nichž nejznámější je změna znaménka takových "vektorů" při transformaci levotočivé na pravotočivou soustavu souřadnic. Známá pravidla pravé a levé ruky užívaná pro určení vektorových součinů v elektromagnetickém poli předpokládají, že pole je popsáno v pravotočivé soustavě souřadnic.
*) V textu této stati se často vyskytují
vedle sebe symboly pro rychlost hmotného bodu
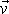 a normálu plochy
a normálu plochy
 ,
které jsou bohužel v použitém typu písma (Times New Roman) velmi podobné,
ale rozlišitelné. Vyzývám proto čtenáře, aby text četl velmi pozorně.
,
které jsou bohužel v použitém typu písma (Times New Roman) velmi podobné,
ale rozlišitelné. Vyzývám proto čtenáře, aby text četl velmi pozorně.
Tento výraz běžně užívaný při středních rychlostech
vzájemného proudění, tj. při Reynoldsových číslech ne příliš podstatně
překračujících kritickou hodnotu Rek
(4,138)
, předpokládá závislost
odporující síly na čtverci rychlosti
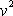 ,
zatímco Stokesův zákon
(4,145)
předpokládá přímou úměrnost mezi silou F a rychlostí
v. Při těchto rychlostech
stanovený součinitel odporu má hodnoty pohybující se od přibližně C
= 1,3 pro polokouli obrácenou dutinou
proti proudu až po hodnotu C = 0,03 pro vhodně volený aerodynamický tvar.
,
zatímco Stokesův zákon
(4,145)
předpokládá přímou úměrnost mezi silou F a rychlostí
v. Při těchto rychlostech
stanovený součinitel odporu má hodnoty pohybující se od přibližně C
= 1,3 pro polokouli obrácenou dutinou
proti proudu až po hodnotu C = 0,03 pro vhodně volený aerodynamický tvar.
Kvadratická závislost odporu prostředí na vzájemné rychlosti prostředí a obtékaného tělesa platí v poměrně úzkém oboru rychlostí. Při podrobnějším zkoumání tvaru závislosti odporu na vzájemné rychlosti chápeme součinitel odporu C jako funkci Reynoldsova čísla a odpor tedy vyjadřujeme závislostí
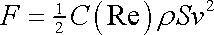 , , |
(4,147) |
přičemž funkce
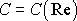 se pro tělesa význačných tvarů (např. pro
obtékanou kouli nebo válec) stanoví experimentálně.
se pro tělesa význačných tvarů (např. pro
obtékanou kouli nebo válec) stanoví experimentálně.
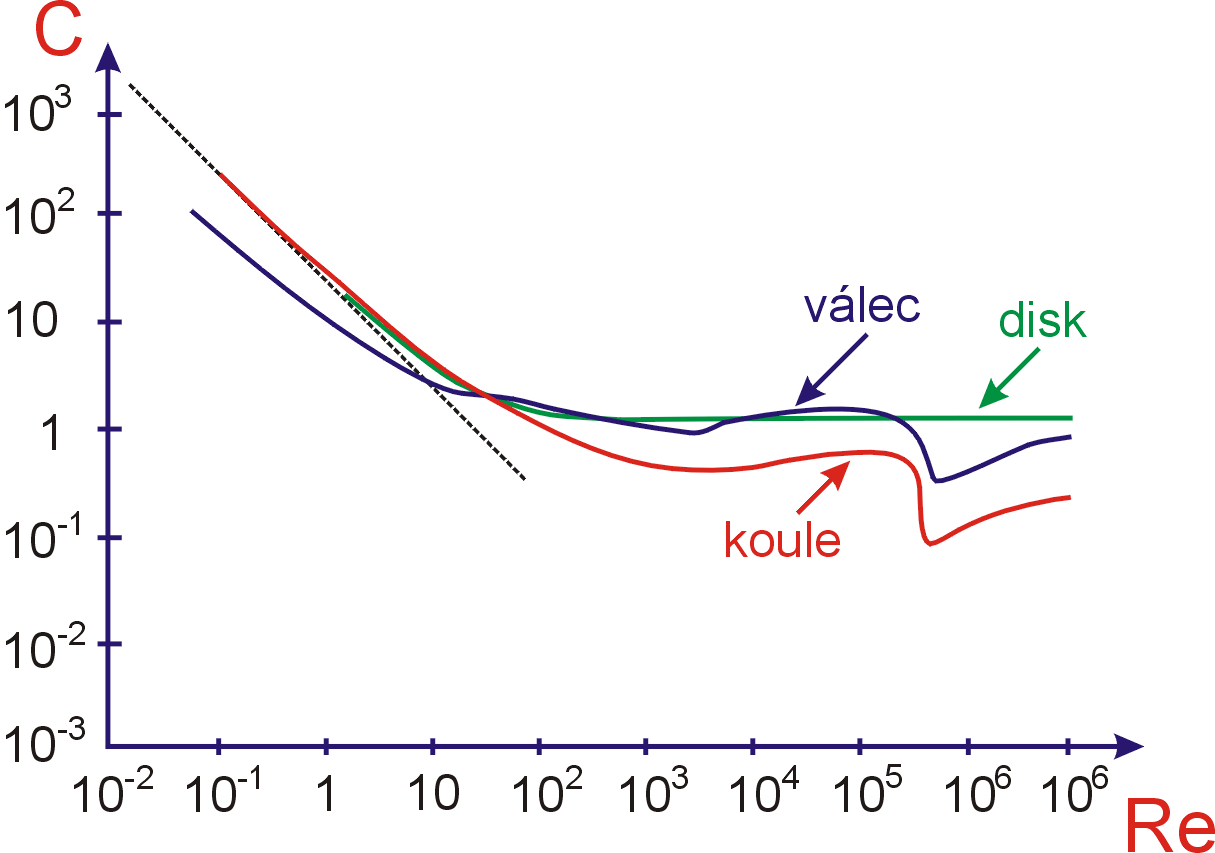 Na obr. 77 je graf závislosti
Na obr. 77 je graf závislosti
 pro obtékaný válec, kouli a disk. Počáteční
pokles funkcí v oblasti Re < 1 odpovídá oboru, kde platí Stokesův zákon
(tečna křivky odpovídající zákonu přesně je vyznačena čárkovaně). Pozvolnější
pokles až do hodnoty
pro obtékaný válec, kouli a disk. Počáteční
pokles funkcí v oblasti Re < 1 odpovídá oboru, kde platí Stokesův zákon
(tečna křivky odpovídající zákonu přesně je vyznačena čárkovaně). Pozvolnější
pokles až do hodnoty
 je přechodovou oblastí mezi platností
Stokesova zákona a Newtonova odporového vzorce. Oblast mezi Re = 103 až 105, kde
hodnota součinitele odporu C
je přibližně konstantní, je oblastí, v které užití Newtonova vzorce
v tvaru
(4,146)
je adekvátní.
V oblasti nad Re = 105 nastane v úzké oblasti prudký pokles
odporu, při kterém součinitel odporu klesne
4 až 5krát. Tento pokles se někdy označuje jako krize odporu a souvisí
se změněným způsobem obtékání tělesa. (Pro disk pohybující ve směru své roviny
pokles nenastává.)
je přechodovou oblastí mezi platností
Stokesova zákona a Newtonova odporového vzorce. Oblast mezi Re = 103 až 105, kde
hodnota součinitele odporu C
je přibližně konstantní, je oblastí, v které užití Newtonova vzorce
v tvaru
(4,146)
je adekvátní.
V oblasti nad Re = 105 nastane v úzké oblasti prudký pokles
odporu, při kterém součinitel odporu klesne
4 až 5krát. Tento pokles se někdy označuje jako krize odporu a souvisí
se změněným způsobem obtékání tělesa. (Pro disk pohybující ve směru své roviny
pokles nenastává.)
Ve sportovním světě se této prudké změny odporu vyžívá např. při smečování ve volejbale. Prudce vypálený míč přeletí síť téměř vodorovně, protože jeho součinitel odporu se pohybuje v nadkritické oblasti a je tedy malý. Za sítí hodnota Reynoldsova čísla poklesne pod kritickou hodnotu, odpor prudce vzroste a míč začne klesat k zemi. Křivka jeho letu je tak velmi vzdálená parabolické dráze, která odpovídá průběhu vrhu, neuvažujeme-li odpor prostředí.
Složitá závislost odporu koule na Reynoldsově čísle vyjádřená grafem z obr.77 je dána výrazně se měnícím způsobem obtékání při různých Reynoldsových číslech. V této stati na příkladu koule uvedeme některé základní pojmy vztahující se ke studiu obtékání těles.
Obtéká-li reálná tekutina, tj. tekutina s nenulovou viskozitou, laminárně nějaké těleso, je na povrchu tělesa vzájemná rychlost proudění a tělesa nulová, tekutina na tělese lpí. V úzké mezní vrstvě dojde k vyrovnání vzájemné rychlosti od nulové hodnoty k hodnotě typické pro hlavní proud obtékající tekutiny. Mezní vrstva obvykle od náběhové části obtékaného tělesa směrem k jeho odvrácené straně se rozšiřuje, laminární mezní vrstva bezprostředně obepínající těleso přechází ve větších vzdálenostech od tělesa v turbulentní mezní vrstvu a posléze se mezní vrstva od tělesa odtrhne a za tělesem nastane oblast turbulentního proudění nazývaná úplav.
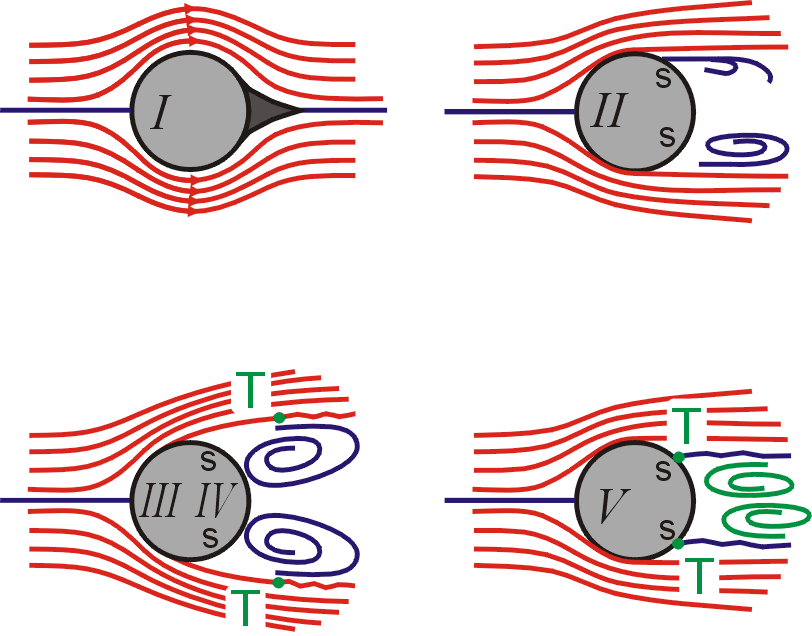 Na obr. 78. jsou znázorněny různé způsoby
obtékání, přičemž stoupající hodnota římské číslice odpovídá vzrůstající
rychlosti obtékání. Způsob obtékání naznačený pro kouli označenou I odpovídá případu, kdy laminární mezní vrstva těsně obepíná kouli,
proudění mimo mezní vrstvu se velmi podobá obtékání ideální tekutinou (srov.
s obtékáním válce vyšetřovaným dále ve statích 4.6.5 a 4.7.2) a odpor
prostředí je dán převážně viskózními, tedy třecími silami. Pro nejnižší hodnoty
Reynoldsova čísla lze tento odpor vystihnout Stokesovým odporovým zákonem
(4,145)
, ale způsob obtékání I se udrží až do
Na obr. 78. jsou znázorněny různé způsoby
obtékání, přičemž stoupající hodnota římské číslice odpovídá vzrůstající
rychlosti obtékání. Způsob obtékání naznačený pro kouli označenou I odpovídá případu, kdy laminární mezní vrstva těsně obepíná kouli,
proudění mimo mezní vrstvu se velmi podobá obtékání ideální tekutinou (srov.
s obtékáním válce vyšetřovaným dále ve statích 4.6.5 a 4.7.2) a odpor
prostředí je dán převážně viskózními, tedy třecími silami. Pro nejnižší hodnoty
Reynoldsova čísla lze tento odpor vystihnout Stokesovým odporovým zákonem
(4,145)
, ale způsob obtékání I se udrží až do
 . Po překročení této hodnoty dojde na zadní
straně koule v místě označeném S k odtržení mezní vrstvy, vytvoření
úplavu (viz obr. koule II) a tlaková složka odporu začne být podstatná. Od minima na křivce
. Po překročení této hodnoty dojde na zadní
straně koule v místě označeném S k odtržení mezní vrstvy, vytvoření
úplavu (viz obr. koule II) a tlaková složka odporu začne být podstatná. Od minima na křivce
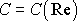 znázorněné na obr.77, tedy od
znázorněné na obr.77, tedy od
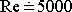 ,
se vytvoří charakter obtékání znázorněný pro kouli označenou III
IV. Způsob značení napovídá, že při podrobnějším zkoumání se
ještě oblast tohoto typu obtékání dělí na dvě, a to na oblast, kde křivka
,
se vytvoří charakter obtékání znázorněný pro kouli označenou III
IV. Způsob značení napovídá, že při podrobnějším zkoumání se
ještě oblast tohoto typu obtékání dělí na dvě, a to na oblast, kde křivka
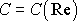 mírně stoupá a oblast, kde její hodnota je
téměř konstantní. My nebudeme obě oblasti rozlišovat a dohromady je budeme
pokládat, za oblast, kde funkce
mírně stoupá a oblast, kde její hodnota je
téměř konstantní. My nebudeme obě oblasti rozlišovat a dohromady je budeme
pokládat, za oblast, kde funkce
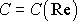 je přibližně konstantní a kde tedy platí
Newtonův odporový vzorec v jednoduchém tvaru
(4,146)
. V této oblasti,
která končí před kritickým poklesem funkce
je přibližně konstantní a kde tedy platí
Newtonův odporový vzorec v jednoduchém tvaru
(4,146)
. V této oblasti,
která končí před kritickým poklesem funkce
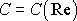 , tj. u hodnoty
, tj. u hodnoty
 je úplav za koulí nejširší a odpor, který je
až z 95% tlakový, je největší. Obtékání po překročení kritického poklesu,
tedy pro Re větší než asi 4.105 , získá charakter znázorněný pro
kouli označenou V . Šířka úplavu se zúží
a tím se zmenší i tlaková odporová síla působící na kouli, která tvoří
rozhodující složku odporu koule.
je úplav za koulí nejširší a odpor, který je
až z 95% tlakový, je největší. Obtékání po překročení kritického poklesu,
tedy pro Re větší než asi 4.105 , získá charakter znázorněný pro
kouli označenou V . Šířka úplavu se zúží
a tím se zmenší i tlaková odporová síla působící na kouli, která tvoří
rozhodující složku odporu koule.
Tlakový odpor vzniká tím, že v oblasti úplavu, kam proudící tekutina proniká s obtížemi, je menší tlak než na čelní stěně obtékaného předmětu. Rozhodující význam tlakové složky odporu odráží Newtonův odporový vzorec
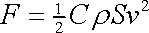 , , |
(4,146) |
který, vydělíme-li jej velikostí S průřezu obtékaného předmětu vystaveného proudu, můžeme přepsat na tvar
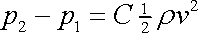 , , |
kde
 je průměrný tlak na té straně předmětu,
která je vystavena proudu a
je průměrný tlak na té straně předmětu,
která je vystavena proudu a
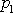 průměrný tlak na odvrácené straně. Poslední
rovnice říká, že rozdíl těchto tlaků je úměrný kinetické energii objemové
jednotky dopadajícího proudu, přičemž konstanta C je konstantou úměrnosti, která závisí na
tvaru obtékaného předmětu.
průměrný tlak na odvrácené straně. Poslední
rovnice říká, že rozdíl těchto tlaků je úměrný kinetické energii objemové
jednotky dopadajícího proudu, přičemž konstanta C je konstantou úměrnosti, která závisí na
tvaru obtékaného předmětu.
Vrátíme se k prudkému poklesu odporu koule
v kritické oblasti funkce
 ,
který nastává přibližně mezi hodnotami Re = 2.105 a Re
= 4.105. Na obr. 78 jsou vyznačena místa odtržení mezní vrstvy
S a místa T, kde dochází k přechodu laminární mezní vrstvy ve vrstvu
turbulentní. V oblasti, kde odpor je velký (koule značená III IV), jsou body S a T vzdáleny a
turbulentní mezní vrstva vzniká daleko za koulí. Dalším zvýšením rychlosti
obtékání dojde v kritické oblasti k splynutí bodu odtržení S a bodu
vzniku turbulentní vrstvy T a poté k vytvoření turbulentní mezní vrstvy na
kouli, která je odolnější vůči odtržení než laminární vrstva. Bod odtržení
mezní vrstvy se posune dále po kouli ve směru rychlosti
,
který nastává přibližně mezi hodnotami Re = 2.105 a Re
= 4.105. Na obr. 78 jsou vyznačena místa odtržení mezní vrstvy
S a místa T, kde dochází k přechodu laminární mezní vrstvy ve vrstvu
turbulentní. V oblasti, kde odpor je velký (koule značená III IV), jsou body S a T vzdáleny a
turbulentní mezní vrstva vzniká daleko za koulí. Dalším zvýšením rychlosti
obtékání dojde v kritické oblasti k splynutí bodu odtržení S a bodu
vzniku turbulentní vrstvy T a poté k vytvoření turbulentní mezní vrstvy na
kouli, která je odolnější vůči odtržení než laminární vrstva. Bod odtržení
mezní vrstvy se posune dále po kouli ve směru rychlosti
 ,
jak je naznačeno při znázornění obtékání koule označené V na obr.78. Úplav za
koulí se tím podstatně zúží.
,
jak je naznačeno při znázornění obtékání koule označené V na obr.78. Úplav za
koulí se tím podstatně zúží.
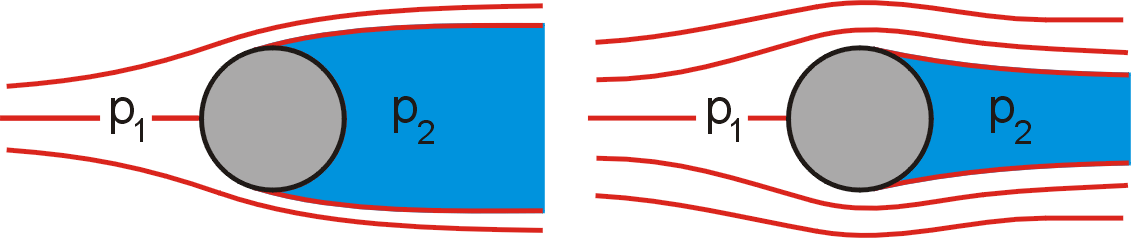
Zúžení úplavu je schematicky znázorněno na obr.79. Obr.79a) ukazuje rozsah úplavu (značen tmavě)
v podkritické oblasti, tj. pro Re menši než v oblasti kritického
poklesu funkce
 ,
a obr.79b) rozsah úplavu
v nadkritické oblasti. V úplavu je podstatně nižší tlak
,
a obr.79b) rozsah úplavu
v nadkritické oblasti. V úplavu je podstatně nižší tlak
 než je tlak
než je tlak
 v části toku před koulí. Podstatné
zúžení úplavu v nadkritické oblasti tak způsobí, že odporová síla, která
je dána násobkem tlaku a plochy úplavu za koulí, výrazně poklesne.
v části toku před koulí. Podstatné
zúžení úplavu v nadkritické oblasti tak způsobí, že odporová síla, která
je dána násobkem tlaku a plochy úplavu za koulí, výrazně poklesne.
Studium obtékání těles je jedna z nejsložitějších a prakticky nejdůležitějších otázek reálné mechaniky tekutin. To, co jsme zde o problému uvedli, je jen úvodem do problematiky, kterou podrobněji můžete nastudovat např. v [34] - [41], [57] a v některých titulech z třetí části seznamu literatury.
Zvláštností silového působení při vzájemném pohybu tělesa a
tekutého prostředí je možnost vzniku silové složky kolmé ke směru vzájemné
rychlosti
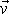 tělesa a prostředí. Tato složka vzniká, když
tvar obtékaného tělesa není symetrický vzhledem ke směru vzájemné rychlosti
nebo když se obtékané těleso otáčí. První případ je bohatě využíván při
konstrukci letadel těžších vzduchu a bude podrobněji probrán v stati
4.6.6. Síla kolmá ke směru pohybu obvykle mířící svisle vzhůru se nazývá vztlakem.
Někdy se označení vztlak užívá v širším slova smyslu pro veškeré odporové
síly mířící kolmo ke vzájemné rychlosti tělesa a prostředí, i když tyto
síly nemíří svisle vzhůru, tedy i v případě těles rotujících kolem
libovolně orientované osy.
tělesa a prostředí. Tato složka vzniká, když
tvar obtékaného tělesa není symetrický vzhledem ke směru vzájemné rychlosti
nebo když se obtékané těleso otáčí. První případ je bohatě využíván při
konstrukci letadel těžších vzduchu a bude podrobněji probrán v stati
4.6.6. Síla kolmá ke směru pohybu obvykle mířící svisle vzhůru se nazývá vztlakem.
Někdy se označení vztlak užívá v širším slova smyslu pro veškeré odporové
síly mířící kolmo ke vzájemné rychlosti tělesa a prostředí, i když tyto
síly nemíří svisle vzhůru, tedy i v případě těles rotujících kolem
libovolně orientované osy.
Druhý případ známý pod názvem Magnusův jev [54] byl aplikován Flettnerem pro pohon a řízení lodí, které měly místo plachet svislé rotující válce. Mnohostranně, většinou zcela intuitivně, je Magnusův jev využíván v míčových hrách, kde roztočením míčů (hovorově falšováním) se dosahuje překvapivých změn jejich dráhy. Ve vojenství se musí se stranovou odchylkou roztočených střel také počítat. Jev je zde označován jako derivace a existují tabulky na jeho kompenzaci i pro střelbu z ručních zbraní. Při dělostřelbě je jeho započtení naprosto nezbytné. Magnusův jev probereme již v následující stati, protože jeho výklad je poněkud jednodušší než výklad vztlaku nad nesymetrickým křídlem.
 Kvalitativně lze vznik Magnusova jevu
pochopit dle obr. 80. Na něm je schematicky znázorněno obtékání rotujícího
válce tekutinou. Rotující válec strhává tekutinu, a proto nad válcem je
proudění rychlejší, proudnice hustší a tlak tedy dle Bernoulliovy rovnice
(4,91)
nižší. Při roztočení válce obtékaného tekutinou vzniká tedy síla kolmá
k rychlosti obtékané tekutiny (uvažuje se rychlost v místech tak
vzdálených od válce, že již přítomnost válce tuto rychlost neovlivňuje), která
v zobrazeném příkladě působí na válec svisle vzhůru.
Kvalitativně lze vznik Magnusova jevu
pochopit dle obr. 80. Na něm je schematicky znázorněno obtékání rotujícího
válce tekutinou. Rotující válec strhává tekutinu, a proto nad válcem je
proudění rychlejší, proudnice hustší a tlak tedy dle Bernoulliovy rovnice
(4,91)
nižší. Při roztočení válce obtékaného tekutinou vzniká tedy síla kolmá
k rychlosti obtékané tekutiny (uvažuje se rychlost v místech tak
vzdálených od válce, že již přítomnost válce tuto rychlost neovlivňuje), která
v zobrazeném příkladě působí na válec svisle vzhůru.
Schematičnost obrázku 80 spočívá v tom, že zobrazuje obtékání tak, jako by se jednalo o obtékání ideální tekutinou. Takový model se sice užívá k elementárnímu vyjádření velikosti Magnusova jevu (4,152) , jak dále ukážeme (viz též stať 4.7.2), ale zcela ignoruje jevy popsané ve statích 4.6.2 a 4.6.3. Symetričnost obrázku podél svislé osy procházející osou válce způsobuje, že z modelu plyne nulová odporová síla namísto realistické odporové síly vyjádřené odporovým vzorcem (4,174) . Neuvažování vzniku mezní vrstvy a úplavu, může v některých případech vést až k tomu, že reálná Magnusova síla bude mít opačné znaménko, než plyne ze vzorce (4,152) odvozeného ze zjednodušeného modelu. Mluvíme pak o inverzním Magnusovu jevu, který je způsoben především nesymetrickým odtrhávání mezní vrstvy.
Podrobně se problematikou Magnusova jevu a jeho aplikací na pohyb rotujících, tedy falšovaných míčů zabýval můj diplomant L. Bernard [58]. Vytvořil počítačový program, který na základě v práci uvedených aproximací pro různé druhy míčů umožňuje předpovídat jejich pohyb, známe-li počáteční rotaci míčů. Program je třeba chápat ne jako definitivní nástroj k stanovení pohybu falšovaných míčů, ale jako interaktivní program, jehož pomocí vypočteme pohyb míče na základě vložených aproximací působících sil, srovnáme jej s experimentálně zjištěným, upřesníme aproximace a tak iterativně získáváme stále lepší shodu výpočtu s experimentem. Tímto postupem také postupně získáme přesnější obraz o silách, které skutečně na rotující míč působí.
Podrobněji se s problematikou Magnusova jevu můžete seznámit např. v právě citované práci [58]. Můžete si tam uvědomit, že už pouhé nahrazení válce míčem, tedy koulí, podstatně zkomplikuje teroretické řešení problému, protože jej již nelze chápat jako rovinný problém (srov. str. 35). Zde uvedeme jen základní odvození velikosti Magnusova jevu, které vychází z modelování děje představou, že nekonečný válec je obtékán ideální tekutinou. Tedy, že obtékání vypadá tak, jak je naznačeno na obr. 80. Je to přístup v mechanice tekutin dosti často užívaný. Jeho oprávněnost podrobněji zhodnotíme v čl. 4.7, především ve stati 4.7.2. Hlavní nedostatky přístupu jsme již výše uvedli a podrobněji jsou rozebrány v [58]. Přesto je důležité odvození uvést, protože nám ukáže, jak lze teoretickými přístupy mechaniky tekutin zdůvodnit podstatu jevu.
Odvození Magnusovy síly užitím modelu obtékání válce ideální tekutinou
Proudění znázorněné na obr. 80, můžeme popsat rychlostním
potenciálem (srov. rov.
(4,49)
- místo obecného označení funkce f budeme dále pro rychlostní potenciál užívat
obvyklého značení
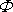 )
)
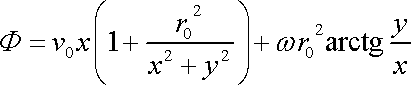 , , |
(4,148) |
který je složením rychlostního potenciálu rovnoměrného proudění (4,183)
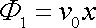 , , |
proudění elementárního dubletu (4,194)
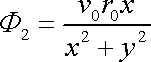 |
a potenciálového víru (4,205)
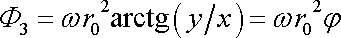 . . |
V posledních třech rovnicích jsme užili neobvyklého odkazování na rovnice dále v textu, protože ve stati 4.7.2, kam je odkazování směřováno, budou uvedené rychlostní potenciály podrobně rozebrány.
V rov.
(4,148)
je
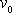 velikost rychlosti proudění v místech
dostatečně vzdálených od válce,
velikost rychlosti proudění v místech
dostatečně vzdálených od válce,
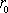 poloměr válce a w úhlová rychlost jeho otáčení; při rotaci
znázorněné na obr.80 je w záporné.
Počátek soustavy souřadnic je volen uprostřed kružnice znázorňující válec, x je vodorovná a y svislá souřadnice, ve vyjádření
potenciálu
poloměr válce a w úhlová rychlost jeho otáčení; při rotaci
znázorněné na obr.80 je w záporné.
Počátek soustavy souřadnic je volen uprostřed kružnice znázorňující válec, x je vodorovná a y svislá souřadnice, ve vyjádření
potenciálu
 je v druhé rovnici užita polární úhlová
souřadnice j.
Volba potenciálu
(4,148)
umožní splnění okrajových podmínek uvažovaného
proudění, kterými jsou rychlost proudění na povrchu válce shodná
s rychlostí válce a rychlost válce v nekonečnu o velikosti
je v druhé rovnici užita polární úhlová
souřadnice j.
Volba potenciálu
(4,148)
umožní splnění okrajových podmínek uvažovaného
proudění, kterými jsou rychlost proudění na povrchu válce shodná
s rychlostí válce a rychlost válce v nekonečnu o velikosti
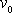 mířící ve směru kladné osy x.
To, že lze do výrazu pro potenciál
mířící ve směru kladné osy x.
To, že lze do výrazu pro potenciál
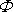 ,
z kterého počítáme rychlost proudění dle vzorce
(4,49)
,
z kterého počítáme rychlost proudění dle vzorce
(4,49)
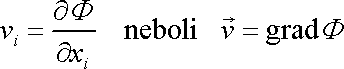 , , |
(4,49) |
zařadit i potenciál víru, rozebereme podrobně ve stati 4.7.2.
Z potenciálu
(4,148)
lze spočítat čtverec velikost
rychlosti
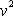 jako
jako
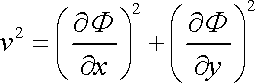 . . |
(4,149) |
Vezmeme-li proudnice těsně obepínající válec shora a zdola a spočteme pro jejich body velikosti rychlosti dle rov. (4,149) , můžeme dle Bernoulliovy rovnice (4,91)
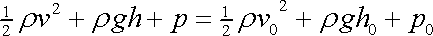 |
(4,150) |
vypočítat rozdíly tlaků
 v jednotlivých bodech těchto proudnic
oproti tlaku
v jednotlivých bodech těchto proudnic
oproti tlaku
 v místech dostatečně vzdálených od
válce. Rozdíly výšek v tíhovém poli
v místech dostatečně vzdálených od
válce. Rozdíly výšek v tíhovém poli
 vedou totiž k zanedbatelným rozdílům
hodnot objemových potenciálních energií
vedou totiž k zanedbatelným rozdílům
hodnot objemových potenciálních energií
 .
Z rozdílu tlaků můžeme integrací podél celého obvodu válce vypočítat
sílu
.
Z rozdílu tlaků můžeme integrací podél celého obvodu válce vypočítat
sílu
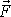 působící na úsek válce délky l
;
působící na úsek válce délky l
;
 . . |
(4,151) |
V poslední rovnici je
 vnější normála válcové plochy v místě,
kde polární úhlová souřadnice má hodnotu
j. Provedeme-li výpočet
dle rovnice
(4,151)
, dostaneme pro velikost síly působící na úsek válce délky l ,
tj. pro velikost Magnusovy síly,
vyjádření
vnější normála válcové plochy v místě,
kde polární úhlová souřadnice má hodnotu
j. Provedeme-li výpočet
dle rovnice
(4,151)
, dostaneme pro velikost síly působící na úsek válce délky l ,
tj. pro velikost Magnusovy síly,
vyjádření
Síla míří ve směru kladné osy y , tj. v případě znázorněném na obr. 80 svisle vzhůru.
Modelujeme-li Magnusův jev jako obtékání nekonečného válce ideální tekutinou, tedy předpokládáme-li, že proudnice mají tvar znázorněný na obr.80, dostaneme početně exaktně zvládnutelný problém, který však vysvětluje jen základní rysy jevu. Ukazuje, že rotací způsobená asymetrie proudění podél osy x vede ke vzniku síly kolmé ke směru vzájemného pohybu válce a tekutiny. Vzhledem k symetrii obrazu proudění podél osy y není model schopen vystihnout reálně bezesporu existující složku síly působící ve směru osy x , tj. odporovou sílu vyjádřenou rovnicí (4,147) . Zcela také ignoruje otázky, o kterých jsme se zmínili ve stati 4.6.3. Mezní vrstva a úplav podstatně od válce oddálí oblast, kde lze proudění alespoň přibližně pokládat za proudění ideální tekutiny, navíc rotace válce způsobí asymetrii v odtrhávání mezní vrstvy vůči ose x , a tím může v nepříznivých případech natolik ovlivnit složku síly kolmou ke směru vzájemného pohybu válce a tekutiny, že síla bude mít nejen zcela jinou hodnotu, ale i opačnou orientaci, než jakou dává modelový výpočet, který vede k rovnici (4,152) . Vznikne tedy výše zmíněný inverzní Magnusův jev.
Na příkladu výpočtu Magnusovy síly (4,152) a rozboru jeho věrohodnosti jsme si naznačili přednosti a nedostatky řešení úloh mechaniky tekutin modelem rovinného proudění ideální tekutiny. Další možnosti tohoto modelu ukážeme v následující stati, když jím vyložíme vznik vztlakové síly při obtékání křídla.
Jako fyzika letu se označuje ta část aerodynamiky, která studuje podmínky letu ptáků a letadel. Základem fyziky letu je vyšetřování sil působících na křídlo obtékané vzduchem. Zde nejprve kvalitativně vysvětlíme, proč křídlo letadlo či ptáka ve vzduchu udrží a jaké síly na ně ve vzduchu působí. Potom stručně naznačíme, jak mechanika tekutin vypočítává užitím modelu ideální tekutiny vztlak, který nadnáší křídlo a jak přejde k realističtějším modelům obtékání, které umožní uvažovat i další síly působící na letící těleso, především odpor proti postupnému pohybu.
Na schematickém obr.81 je znázorněn profil křídla a proudnice vystihující vzájemný pohyb křídla a obtékajícího vzduchu. Je na něm naznačen případ, kdy spodní plocha křídla je vodorovná, tedy dále definovaný náběhový úhel a nulový. I v tomto případě vznikne vztlaková síla udržující křídlo ve vzduchu. Asymetrický tvar křídla způsobí zhuštění proudnic nad vypuklou horní plochou oproti jejich vzdálenostem v oblasti pod rovinnou spodní plochou křídla. Dle Bernoulliovy rovnice (4,91) zhuštění proudnic nad křídlem odpovídá zvýšení rychlosti a tím snížení tlaku nad křídlem oproti tlaku, který je pod křídlem. Při aplikaci Bernoulliovy rovnice předpokládáme, že v místech dostatečně vzdálených od křídla, jsou tlak a vzájemná rychlost pro všechny proudnice stejné a rozdíly v nadmořské výšce zanedbatelné.

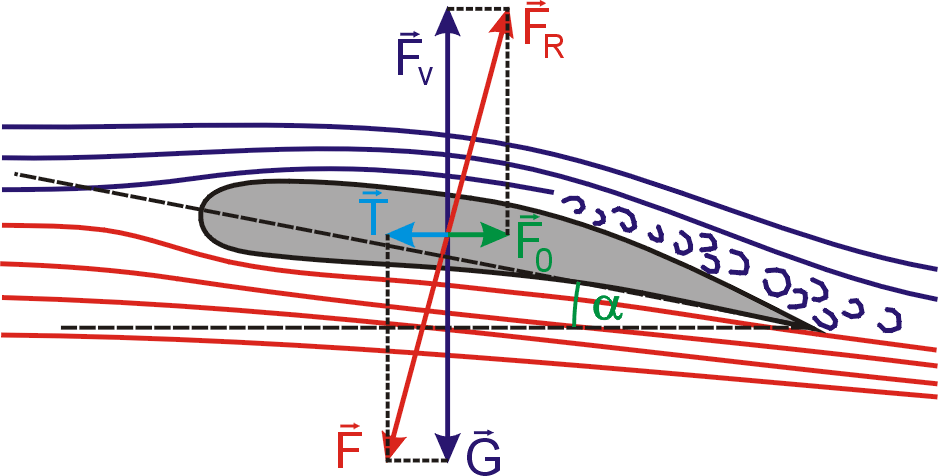 Na obr.82 jsou znázorněny síly, které působí
na křídlo obtékané vzduchem. Kromě již zmíněné vztlakové síly
Na obr.82 jsou znázorněny síly, které působí
na křídlo obtékané vzduchem. Kromě již zmíněné vztlakové síly
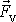 ,
která působí proti tíhové síle
,
která působí proti tíhové síle
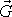 a udržuje letící těleso ve vzduchu, je to
odporová síla
a udržuje letící těleso ve vzduchu, je to
odporová síla
 ,
jejíž velikost se určuje způsobem vyloženým ve stati 4.6.2. Celková reakční
síla
,
jejíž velikost se určuje způsobem vyloženým ve stati 4.6.2. Celková reakční
síla
 působící na křídlo je při rovnoměrném letu
kompenzována výslednicí
působící na křídlo je při rovnoměrném letu
kompenzována výslednicí
 tíhy letadla
tíhy letadla
 a tažné síly
a tažné síly
 přenesené na křídlo. Vztlaková síla
přenesené na křídlo. Vztlaková síla
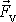 závisí na tvaru křídla a též na úhlu náběhu a , který je znázorněn
na obr.82. Vztlaková síla je kladná (míří vzhůru) od mírně záporných hodnot
úhlu a a svého maxima dosahuje v okolí
závisí na tvaru křídla a též na úhlu náběhu a , který je znázorněn
na obr.82. Vztlaková síla je kladná (míří vzhůru) od mírně záporných hodnot
úhlu a a svého maxima dosahuje v okolí
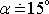 .
Při takto vysokých hodnotách úhlu náběhu již podstatně roste odporová síla
.
Při takto vysokých hodnotách úhlu náběhu již podstatně roste odporová síla
 a let se stává nestabilním. Případ nulového
úhlu náběhu
a let se stává nestabilním. Případ nulového
úhlu náběhu
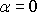 je zobrazen
na obr.81 a rozebrán v textu k tomuto obrázku.
je zobrazen
na obr.81 a rozebrán v textu k tomuto obrázku.
Jak dále ukážeme, použijeme-li k výkladu vztlaku model ideální tekutiny, dostaneme podobně jako v případě Magnusova jevu (stať 4.6.5) nulovou odporovou sílu. K výpočtu reálných odporových sil musíme užít modely proudění zmíněné ve stati 4.6.3. Ve fyzice letu je však nyní třeba zkoumat i lety nadzvukovou rychlostí, tedy lety, kdy Machovo číslo Ma (4,143) má hodnotu větší než 1. V takových případech musíme Machovo číslo zařadit do podobnostních úvah (stať 4.5.3) a už ani metody naznačené ve stati 4.6.3 nestačí a je třeba budovat novou aerodynamiku nadzvukových rychlostí (např.[59]).
Žukovského transformace
Rovnice (4,148) určuje rychlostní potenciál pro obtékání rotujícího válce. Analogii vzniku vztlakové síly (Magnusovy síly) při tomto obtékání a obtékání křídla (asymetrického tvaru vloženého do proudu) lze dobře teoreticky zdůvodnit. Aby funkce (4,148) byla potenciálem popisujícím zadaný typ proudění, musí splňovat okrajové podmínky problému a musí být harmonickou funkcí, tj. splňovat podmínku
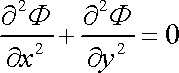 |
(4,153) |
v celé oblasti, kde popisuje proudění. Pro rovinné
proudění platí důležité pravidlo (viz. např. [1], čl..15.5 nebo [60]),
které říká, že řeší-li potenciál
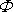 problém proudění v jistém geometrickém
uspořádání, bude ho řešit i v geometrickém uspořádání, které
z původního vznikne konformním zobrazením. Podrobněji problematiku
konformního zobrazení probereme ve stati 4.7.2.
problém proudění v jistém geometrickém
uspořádání, bude ho řešit i v geometrickém uspořádání, které
z původního vznikne konformním zobrazením. Podrobněji problematiku
konformního zobrazení probereme ve stati 4.7.2.
Konformní zobrazení zachovává úhly mezi zobrazovanými přímkami,
v případě proudění pravé úhly mezi proudnicemi a ekvipotenciálními plochami
rychlostního potenciálu
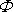 .
Konformní zobrazení převádějící obtékání rotujícího válce na obtékání tělesa
tvaru, kterým lze modelovat profil křídla, lze přehledně vyjádřit jako
zobrazení komplexní roviny
.
Konformní zobrazení převádějící obtékání rotujícího válce na obtékání tělesa
tvaru, kterým lze modelovat profil křídla, lze přehledně vyjádřit jako
zobrazení komplexní roviny
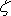 do komplexní roviny z dané funkcí
do komplexní roviny z dané funkcí
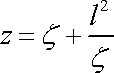 . . |
(4,154) |
 Pro zobrazení
(4,154)
, kde l je reálná konstanta rozměru délky, se užívá název Žukovského transformace.
Zvolíme-li v rovině
Pro zobrazení
(4,154)
, kde l je reálná konstanta rozměru délky, se užívá název Žukovského transformace.
Zvolíme-li v rovině
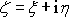 vhodným způsobem kružnici k bude jejím obrazem v rovině
vhodným způsobem kružnici k bude jejím obrazem v rovině
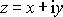 tvar podobný křídlu, jak je naznačeno na
obr.83. Na plně vytažený obrys "křídla" se zobrazuje plně vyznačená
kružnice k se středem
v bodě S. Na obrázku je ještě
čárkovaně zobrazena kružnice se středem
P, která se zobrazí na čárkovaný oblouk začínající v bodě B a
končící v bodě A. (podrobně viz [1], čl. 15.5). Na obr. 84 je
ukázáno, jak se při tomto zobrazení budou transformovat proudnice a
ekvi-potenciální plochy. Úhlová rychlost otáčení válce w v předlohové rovině
tvar podobný křídlu, jak je naznačeno na
obr.83. Na plně vytažený obrys "křídla" se zobrazuje plně vyznačená
kružnice k se středem
v bodě S. Na obrázku je ještě
čárkovaně zobrazena kružnice se středem
P, která se zobrazí na čárkovaný oblouk začínající v bodě B a
končící v bodě A. (podrobně viz [1], čl. 15.5). Na obr. 84 je
ukázáno, jak se při tomto zobrazení budou transformovat proudnice a
ekvi-potenciální plochy. Úhlová rychlost otáčení válce w v předlohové rovině
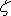 byla volena tak, aby při trans-formaci na
profil "křídla" byla rychlost u jeho zadní ostré hrany konečná (srov. [1], čl.
15.6).
byla volena tak, aby při trans-formaci na
profil "křídla" byla rychlost u jeho zadní ostré hrany konečná (srov. [1], čl.
15.6).
Podél "křídla" se rychlost rozloží tak, aby cirkulace rychlosti (srov. (4,162) ) podél křivky ohraničující profil křídla
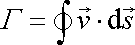 |
(4,155) |
byla stejná jako cirkulace
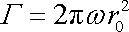 |
(4,156) |
podél kružnice reprezentující profil válce v předlohové
rovině
 .
Ze složek skládajících rychlostní potenciál
(4,148)
jedině potenciálový vír má
cirkulaci různou od nuly. Proto cirkulace
(4,156)
rychlostního potenciálu je
shodná s cirkulací potenciálového víru, kterou lze jednoduše vypočítat
jako násobek konstantní rychlosti
.
Ze složek skládajících rychlostní potenciál
(4,148)
jedině potenciálový vír má
cirkulaci různou od nuly. Proto cirkulace
(4,156)
rychlostního potenciálu je
shodná s cirkulací potenciálového víru, kterou lze jednoduše vypočítat
jako násobek konstantní rychlosti
 na proudnici obepínající rotující válec
násobený délkou této proudnice (srov.
(4,205)
), tedy
na proudnici obepínající rotující válec
násobený délkou této proudnice (srov.
(4,205)
), tedy
 , , |
jak jsme již uvedli v rovnici (4,156) .
Jak v případě předlohové roviny popisující problém Magnusova jevu, tak i v případě transformované roviny popisující obtékání křídla, je absolutní hodnota součinu rychlosti a délky hraniční křivky (válce, resp. "křídla") na vrchní straně křivek větší než na spodní straně. Proto výsledná cirkulace je nenulová.
Konformním zobrazením se cirkulace nemění, jak jsme již mlčky předpokládali při úvaze o rozložení rychlosti podél křídla uvedené před rovnicí (4,156) . Vztlaková síla působící na "křídlo" je tedy dána stejným výrazem jako Magnusova síla (4,152) . Na úsek "křídla" délky l (rozumí se úsek kolmý na vyšetřovanou rovinu) působí síla
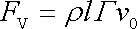 ,. ,. |
(4,157) |
kde r je hustota obtékajícího prostředí,
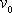 vzájemná rychlost prostředí a křídla
v místech dostatečně vzdálených od "křídla". Shodnost výsledku se stane
zřejmou, až když si uvědomíme, že ve výrazu
(4,152)
můžeme dle
(4,156)
za
vzájemná rychlost prostředí a křídla
v místech dostatečně vzdálených od "křídla". Shodnost výsledku se stane
zřejmou, až když si uvědomíme, že ve výrazu
(4,152)
můžeme dle
(4,156)
za
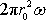 dosadit cirkulaci G.
dosadit cirkulaci G.
 Velikost
G volíme tak, aby byla splněna podmínka
konečné rychlosti u hrany "křídla", jak bylo zmíněno na konci odstavce za rov.
(4,154)
. Touto podmínkou určujeme rychlost rotace a tím i cirkulaci válce,
který transformujeme na "křídlo", a tak i velikost vztlaku, který daný profil
křídla vytváří při rychlosti
Velikost
G volíme tak, aby byla splněna podmínka
konečné rychlosti u hrany "křídla", jak bylo zmíněno na konci odstavce za rov.
(4,154)
. Touto podmínkou určujeme rychlost rotace a tím i cirkulaci válce,
který transformujeme na "křídlo", a tak i velikost vztlaku, který daný profil
křídla vytváří při rychlosti
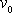 .
Tu můžeme standardizovat a porovnávat tak výhodnost různých profilů.
.
Tu můžeme standardizovat a porovnávat tak výhodnost různých profilů.
V uvažovaném modelu je vztlaková síla (4,157) , která působí kolmo na směr proudění, opět jedinou sílu, kterou prostředí na "křídlo" působí. Velice podstatnou odporovou složku působící ve směru proudění uvedený model vysvětlit nedokáže. Vyloženým postupem se nám tedy jen podařilo ukázat, že vznik vztlakové síly při obtékání nesymetrického tělesa (např. křídla) lze vysvětlit modelem ideální tekutiny. Pro realističtější popis dějů, které při obtékání křídel a celého letícího tělesa nastávají, je tedy minimálně nutno použít postupy naznačené ve stati 4.6.3 a doplnit je dalšími převážně experimentálními metodami. Podrobněji se lze o této problematice poučit např. v [35], [36], [37], [38].