Hlavním úkolem tohoto druhého dílu knihy Klasická mechanika bylo ukázat jednotnou strukturu mechaniky kontinua a s touto strukturou čtenáře obeznámit tak, aby s ní uměli aktivně pracovat. V části věnované mechanice tekutin tento přístup byl aplikován v prvních čtyrech článcích. Články 4.5 a 4.6 ukázaly možnosti a meze takového přímočarého postupu. Meze přímočarého postupu jsou ve všech oblastech mechaniky kontinua, ale v mechanice tekutin jsou natolik významné, že není možné se o nich nezmínit.
Vznik turbulence znamená, že je porušen základní předpoklad mechaniky kontinua, tj. předpoklad o spojitém rozložení kontinua. Turbulencí se spojitý proud tekutiny roztrhá a z kontinua se stane diskontinuum. Rovnice mechaniky kontinua přestávají platit a je třeba je nahradit při vyšetřování turbulentního proudění jinými postupy (viz např. [40], [41], srov. též třetí část seznamu literatury). Při vyšetřování odporu prostředí v čl. 4.6 jsme uvedli, že z Navierovy-Stokesovy rovnice ( (4,116) , resp. (4,118) ) lze sice odvodit Stokesův odporový zákon (4,145) , ale pro vysvětlení odporu při větších vzájemných rychlostech proudění a obtékaného tělesa již takový přístup selhává (viz stať 4.6.2) a je třeba zavést nové představy stručně uvedené ve stati 4.6.3. Rozložení a charakter mezních vrstev a úplavů při obtékání těles nelze odvodit ze základních rovnic mechaniky kontinua a při řešení reálných úloh, např. při stanovení aerodynamického odporu automobilů je třeba postupovat semiempirickým způsobem. V posledních třech statích čl. 4.6 jsme na příkladu Magnusova jevu a obtékání křídla ukázali, jak model rovinného proudění ideální tekutiny umí velmi elegantně vysvětlit vznik vztlakové síly v obou případech, ale naprosto selže při výkladu odporu ve směru proudění, pro který udá zcela nerealistickou nulovou hodnotu.
Podobných případů, kdy k řešení reálných úloh proudění tekutin nestačí strohá aplikace zákonů mechaniky kontinua, je velmi mnoho. V některých případech se problém řeší tak, že závěry plynoucí z teorie potenciálového proudění se převádějí na reálný případ předpokladem, že mimo tenkou mezní vrstvu vznikne relativně snadno popsatelné potenciálové proudění (může k němu přispět i potenciálový vír) a hlavní závěry plynoucí z takto popsaného proudění platí. Při vyšetřování Magnusova jevu a obtékání křídla jsme takto vysvětlili působící vztlak. Aby použité metody byly snáze pochopitelné, vyložíme ve statích 4.7.1 a 4.7.2 základy teorie vířivého proudění a popisu rovinného proudění komplexními funkcemi. K vysvětlení reálně velmi významného odporu válce a křídla musíme model užitý v čl.4.6.5, resp. 4.6.6, doplnit o mezní vrstvy a úplavy, které vznikají mezi tělesy a oblastmi, kde lze proudění za potenciálové pokládat. Odpor pak vysvětlíme obdobně, jako jsme to činili ve stati 4.6.3, tj. např. vznikem podtlaku v turbulentních oblastech za tělesy, tedy již mimo rámec přímočaré mechaniky kontinua.
Řešením technických problémů proudění tekutin, kde teoretický přístup mechaniky kontinua dává pouze základní rámec řešení a teorií kontinua nezahrnuté aspekty jsou podstatné, se zabývá hydraulika. Ve stati 4.7.3 hydrauliku představíme a v následujících statích tohoto článku rozebereme některé prakticky důležité případy proudění, pro jejichž popis je třeba přístup mechaniky kontinua doplnit pohledem hydrauliky.
Ve stati 4.3.1 jsme rozdělili proudění na potenciálové a
vířivé, načež v rovnici
(4,148)
jsme do potenciálu zařadili člen
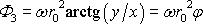 označený jako potenciálový vír. Dále jsme pak
ve statích 4.6.5 a 4.6.6 užívali poněkud intuitivně popis rovinného proudění
komplexními funkcemi komplexní proměnné. Intuitivní postup jsme zvolili, aby základní
body postupu, tj. modelování obtékání rotujícího válce potenciálovým prouděním
ideální tekutiny a jeho transformace na případ obtékání křídla vynikly a nebyly
při výkladu rozmělněny rozebíráním užitého matematického aparátu a obecných
teoretických představ mechaniky tekutin. Tento chybějící rozbor nyní
v této a následující stati doplníme.
označený jako potenciálový vír. Dále jsme pak
ve statích 4.6.5 a 4.6.6 užívali poněkud intuitivně popis rovinného proudění
komplexními funkcemi komplexní proměnné. Intuitivní postup jsme zvolili, aby základní
body postupu, tj. modelování obtékání rotujícího válce potenciálovým prouděním
ideální tekutiny a jeho transformace na případ obtékání křídla vynikly a nebyly
při výkladu rozmělněny rozebíráním užitého matematického aparátu a obecných
teoretických představ mechaniky tekutin. Tento chybějící rozbor nyní
v této a následující stati doplníme.
Ve stati 4.3.1, jsme proudění rozdělili na vířivé a
nevířivé. Ukázali jsme, že pro nevířivé proudění lze v celé oblasti, kde
je definováno, zavést potenciál, z kterého je možno dle rov.
(4,49)
určit
rychlost proudění v každém bodě oblasti. Proto jsme dále pro nevířivé
proudění užívali i označení potenciálové proudění a obvykle mlčky
předpokládali, že definiční oblastí je celý prostor. Obecnými vlastnostmi vířivého
proudění jsme se podrobněji nezabývali. V některých případech má proudění,
které se z pohledu celého prostoru jeví jako vířivé, oblast, kde vír
rychlosti
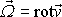 je nenulový, velmi omezenou. Mimo tuto
oblast můžeme pak zavést potenciál rychlosti. Taková oblast však nikdy nemůže
být celým prostorem. To je případ potenciálového víru zmíněného na začátku této
stati. Oblast, pro kterou jej užíváme je vnějšek válce, tedy do celého prostoru
chybí vnitřek válce. V matematické formulaci (viz např. [9],
čl.22.1) říkáme, že se jedná o dvojnásobně souvislou oblast. Podrobně
potenciálový vír probereme v následující stati (viz rov.
(4,199)
a další).
je nenulový, velmi omezenou. Mimo tuto
oblast můžeme pak zavést potenciál rychlosti. Taková oblast však nikdy nemůže
být celým prostorem. To je případ potenciálového víru zmíněného na začátku této
stati. Oblast, pro kterou jej užíváme je vnějšek válce, tedy do celého prostoru
chybí vnitřek válce. V matematické formulaci (viz např. [9],
čl.22.1) říkáme, že se jedná o dvojnásobně souvislou oblast. Podrobně
potenciálový vír probereme v následující stati (viz rov.
(4,199)
a další).
Nyní si všimneme blíže vířivého proudění. Ve vířivém
proudění můžeme vedle proudnic a proudových trubic zavést vírové čáry a vírové
trubice. Vírová čára je křivka,
k níž vír rychlosti
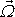 je vždy tečný. V analogii
s rovnicí proudnice
(1,4)
můžeme rovnici vírové čáry zapsat v tvaru
je vždy tečný. V analogii
s rovnicí proudnice
(1,4)
můžeme rovnici vírové čáry zapsat v tvaru
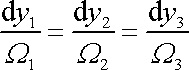 . . |
(4,158) |
Vírové čáry v tekutině jsou uzavřené křivky, případně, uvažujeme-li proudění v omezené oblasti, křivky, které probíhají tekutinou od jedné hranice tekutiny k druhé. Tato vlastnost znamená, že vírové čáry nikde v sledované oblasti nezačínají ani nekončí, tedy nemají v ní zdroj (srov. proudění zdroje - obr.88 a výklad k němu). Říkáme, že pole víru rychlosti je nezdrojové nebo obvykleji nezřídlové. Pro vír rychlosti totiž platí
 , , |
(4,159) |
neboť z vektorové analýzy (např. [9] čl.7.2) plyne, že platí
identicky
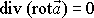 .
Je-li divergence vektoru
.
Je-li divergence vektoru
 v nějakém bodě různá od nuly,
v nějakém bodě různá od nuly,
 ,
má vektor v tomto bodě zdroj. Je-li, jak udává rovnice
(4,159)
,
,
má vektor v tomto bodě zdroj. Je-li, jak udává rovnice
(4,159)
,
 ,
nemůže vírová čára mít žádný zdroj.
,
nemůže vírová čára mít žádný zdroj.
Analogicky, jako jsme v poli proudnic zavedli pojem proudová trubice (viz stať 4.3.2), zavedeme
v poli vírových čar pojem vírová
trubice. Je to myšlená trubice, jejíž površky tvoří vírové čáry. Rovnici
kontinuity proudění (stať 4.3.2) lze formulovat i tak, že hmotnostní tok
(4,55)
různými průřezy proudové trubice je stejný. Analogicky pro vírovou trubici
platí, že tok víru rychlosti
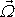 jejími různými průřezy je stejný. Protože
platí rov.
(4,159)
, plyne bezprostředně z Gaussovy věty (viz poznámku na str.106), že tok víru
rychlosti libovolnou uzavřenou plochou je nulový;
jejími různými průřezy je stejný. Protože
platí rov.
(4,159)
, plyne bezprostředně z Gaussovy věty (viz poznámku na str.106), že tok víru
rychlosti libovolnou uzavřenou plochou je nulový;
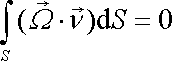 . . |
(4,160) |
 Na obr.85 je znázorněna
vírová trubice. Aplikujeme-li na ní rovnici
(4,160)
je zřejmé, že tok víru
průřezem S1 musí být stejný jako tok průřezem S2. Tok povrchem trubice je
nulový, protože vnější normála
Na obr.85 je znázorněna
vírová trubice. Aplikujeme-li na ní rovnici
(4,160)
je zřejmé, že tok víru
průřezem S1 musí být stejný jako tok průřezem S2. Tok povrchem trubice je
nulový, protože vnější normála
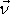 je kolmá k vektoru
je kolmá k vektoru
 ,
který má směr površky trubice. Toky průřezy
S1 a S2 tak musí v součtu dát nulu požadovanou rovnicí
(4,160)
. Jsou
tedy stejně velké a opačného znaménka, protože u průřezu S1 vnější normála je opačně orientovaná a u průřezu S2 souhlasně orientovaná s vektorem víru rychlosti
,
který má směr površky trubice. Toky průřezy
S1 a S2 tak musí v součtu dát nulu požadovanou rovnicí
(4,160)
. Jsou
tedy stejně velké a opačného znaménka, protože u průřezu S1 vnější normála je opačně orientovaná a u průřezu S2 souhlasně orientovaná s vektorem víru rychlosti
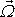 .
Při interpretaci toku trubicí však u všech průřezů pokládáme normálu za
orientovanou ve směru vektoru, jehož tok uvažujeme. Proto můžeme získaný
výsledek interpretovat tak, že tok vektoru víru rychlosti všemi průřezy vírové
trubice je stejný.
.
Při interpretaci toku trubicí však u všech průřezů pokládáme normálu za
orientovanou ve směru vektoru, jehož tok uvažujeme. Proto můžeme získaný
výsledek interpretovat tak, že tok vektoru víru rychlosti všemi průřezy vírové
trubice je stejný.
Tok víru rychlosti průřezem vírové trubice, tj. výraz
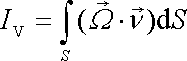 |
(4,161) |
přes průřez proudové trubice, se nazývá intenzita vírové trubice nebo stručněji intenzita víru. Výsledek můžeme formulovat jako větu:
Intenzita víru
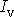 podél vírové trubice se zachovává. Tato věta
bývá označována jako Helmholtzova druhá
věta.
podél vírové trubice se zachovává. Tato věta
bývá označována jako Helmholtzova druhá
věta.
 Z druhé věty
Helmholtzovy plyne, že vírová trubice se zužuje, když velikost víru rychlosti
roste a naopak. V užších místech trubice je rychlost otáčení větší. Podobně
jako vírová čára ani vírová trubice nemůže v ideální tekutině končit
uvnitř oblasti proudění. Musí tvořit buď uzavřené prstence nebo končit na
stěnách nádoby či na volné hladině. Připomínám, že se v posledních
článcích za-býváme výlučně stacio-nárním prouděním, a proto uvažujeme jen
zachování intenzity víru v prostoru. O chování vírů
v nestacio-nárním proudění se lze poučit např. v [1], kap.16.
Z druhé věty
Helmholtzovy plyne, že vírová trubice se zužuje, když velikost víru rychlosti
roste a naopak. V užších místech trubice je rychlost otáčení větší. Podobně
jako vírová čára ani vírová trubice nemůže v ideální tekutině končit
uvnitř oblasti proudění. Musí tvořit buď uzavřené prstence nebo končit na
stěnách nádoby či na volné hladině. Připomínám, že se v posledních
článcích za-býváme výlučně stacio-nárním prouděním, a proto uvažujeme jen
zachování intenzity víru v prostoru. O chování vírů
v nestacio-nárním proudění se lze poučit např. v [1], kap.16.
Intenzitu vírové trubice
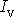 určíme z rychlosti tekutiny na plášti
trubice. Vypočteme křivkový integrál podél uzavřené křivky k ohraničující průřez S trubice z průmětu rychlosti
určíme z rychlosti tekutiny na plášti
trubice. Vypočteme křivkový integrál podél uzavřené křivky k ohraničující průřez S trubice z průmětu rychlosti
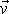 do směru křivky
do směru křivky
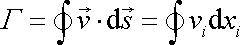 , , |
(4,162) |
který se nazývá cirkulace
rychlosti. K zavedení cirkulace je připojen ilustrační obr.86; způsob
zavedení křivkového integrálu porovnejte s I, čl. 3.1, kde bylo podrobně
ukázáno, jak průmět síly do směru křivky definuje práci. Dle Stokesovy věty
(např. [9], čl.
7.3), která říká, že integrál z rotace vektoru
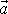 přes plochu
S (normála plochy je označena
přes plochu
S (normála plochy je označena
 ) ohraničenou křivkou k je
roven cirkulaci vektoru
) ohraničenou křivkou k je
roven cirkulaci vektoru
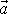 podél této uzavřené křivky, dostáváme
v našem případě
podél této uzavřené křivky, dostáváme
v našem případě
 . . |
(4,163) |
Z rovnice (4,163) plyne tedy důležitý závěr:
Intenzita vírové trubice
 je rovna cirkulaci rychlosti G podél libovolné uzavřené křivky obepínající
trubici.
je rovna cirkulaci rychlosti G podél libovolné uzavřené křivky obepínající
trubici.
Na konci první kapitoly jsme zavedli pojem rovinné napětí (viz rov. (1,90) ) a ukázali jsme si, jak některé pojmy lze pro takové napětí snáze vysvětlit, než když uvažujeme obecné prostorové napětí. Nyní na příkladu rovinného proudění si naznačíme, jak pro rovinný případ lze užít komplexní funkce komplexní proměnné k řešení úloh mechaniky kontinua. Intuitivně jsme již metodu užili ve statích 4.6.5 a 4.6.6. Nyní si poněkud systematičtěji probereme její základy.
Rovinné proudění je takové proudění tekutiny, při kterém
vektory rychlostí všech částic tekutiny leží v jedné rovině. Položíme-li
do této roviny osy x a y kartézské souřadnicové soustavy, mají
vektory rychlosti částic nenulové pouze složky
 a tyto složky jsou funkcemi pouze těchto dvou souřadnic. Složky
a tyto složky jsou funkcemi pouze těchto dvou souřadnic. Složky
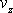 jsou identicky rovny nule. Rovnicemi
jsou identicky rovny nule. Rovnicemi
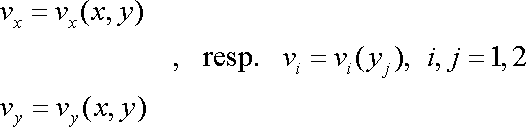 |
(4,164) |
je proudění popsáno. Stačí je tedy vyšetřovat pouze v rovině. Ve směru kolmém na tuto rovinu, tj. ve směru osy z , resp. třetí osy, se obraz proudění nemění. Teoreticky uvažujeme, že proudění ve směru osy z pokračuje do nekonečna, ale při interpretaci nahrazujeme obecné válcové plochy jejich průsečnicemi s rovinou x,y a o rovinách mluvíme běžně jako o křivkách. Při interpretaci výsledků rovinného proudění potom musíme dát pozor na fyzikální rozměr uvažovaných veličin.
Pro popis rovinného potenciálového proudění je vhodné zavést vedle rychlostního potenciálu (4,49) (viz též poznámku o symbolu rychlostního potenciálu před rovnicí (4,148) )
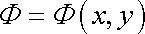 |
(4,165) |
také proudovou funkci
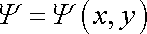 . . |
(4,166) |
Plochy stálé hodnoty rychlostního potenciálu
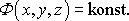 ,
tedy ekvipotenciální plochy, jsou kolmé k rychlosti proudění a při popisu
rovinného proudění se redukují na ekvipotenciální křivky
,
tedy ekvipotenciální plochy, jsou kolmé k rychlosti proudění a při popisu
rovinného proudění se redukují na ekvipotenciální křivky
 Proudová funkce
Proudová funkce
 je zavedena tak, že jejími křivkami stálé
hodnoty jsou proudnice, pro které dle rov.
(1,5)
v rovinném případě platí
je zavedena tak, že jejími křivkami stálé
hodnoty jsou proudnice, pro které dle rov.
(1,5)
v rovinném případě platí
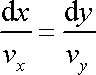 . . |
(4,167) |
Gradient (srov. I, stať 3.4.4) funkce
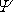 je kolmý k její křivce stálé hodnoty,
tedy k proudnici;
je kolmý k její křivce stálé hodnoty,
tedy k proudnici;
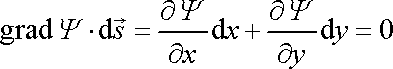 , , |
(4,168) |
kde
 je elementární vektor ve směru proudnice.
Porovnáme-li rov.
(4,168)
s rovnicí
je elementární vektor ve směru proudnice.
Porovnáme-li rov.
(4,168)
s rovnicí
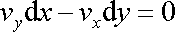 , , |
(4,169) |
která bezprostředně plyne z rovnice
(4,167)
, vidíme, že
pro složky gradientu funkce
 dostáváme vyjádření
dostáváme vyjádření
Z definice
rychlostního potenciálu
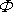 plyne, že jeho gradient dává rychlost
proudění, tedy
plyne, že jeho gradient dává rychlost
proudění, tedy
 . . |
(4,170) |
Z rovnic (4,169) a (4,170) vyplývá, že gradienty obou funkcí jsou vzájemně kolmé, neboť platí
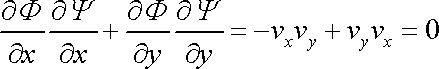 . . |
Kolmé jsou tedy i křivky stálých hodnot obou funkcí, tj. proudnice a ekvipotenciální křivky rychlostního potenciálu, pro které platí
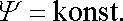 |
(4,171) |
a
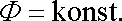 |
(4,172) |
Hodnoty konstant jsou zřejmě různé pro jednotlivé proudnice a ekvipotenciální křivky.
Vykreslením sítě obou křivek stálé hodnoty
(4,171)
a
(4,172)
lze podat výstižný obraz proudění. Na obr.87 je takto znázorněné rovnoměrné proudění ve směru osy x.
Jako rovnoměrné označujeme proudění, které má ve všech bodech prostoru stejnou
hodnotu vektoru rychlosti na obrázku označenou
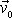 .
Na obr.88 je znázorněno proudění zdroje, který leží v počátku soustavy
souřadnic. Toto radiální proudění míří od počátku v případě, že ze zdroje tekutina vytéká nebo do počátku
v případě, že tekutina je zdrojem pohlcována. V prvním případě
nazýváme zdroj zřídlem,
v druhém propadem.
.
Na obr.88 je znázorněno proudění zdroje, který leží v počátku soustavy
souřadnic. Toto radiální proudění míří od počátku v případě, že ze zdroje tekutina vytéká nebo do počátku
v případě, že tekutina je zdrojem pohlcována. V prvním případě
nazýváme zdroj zřídlem,
v druhém propadem.
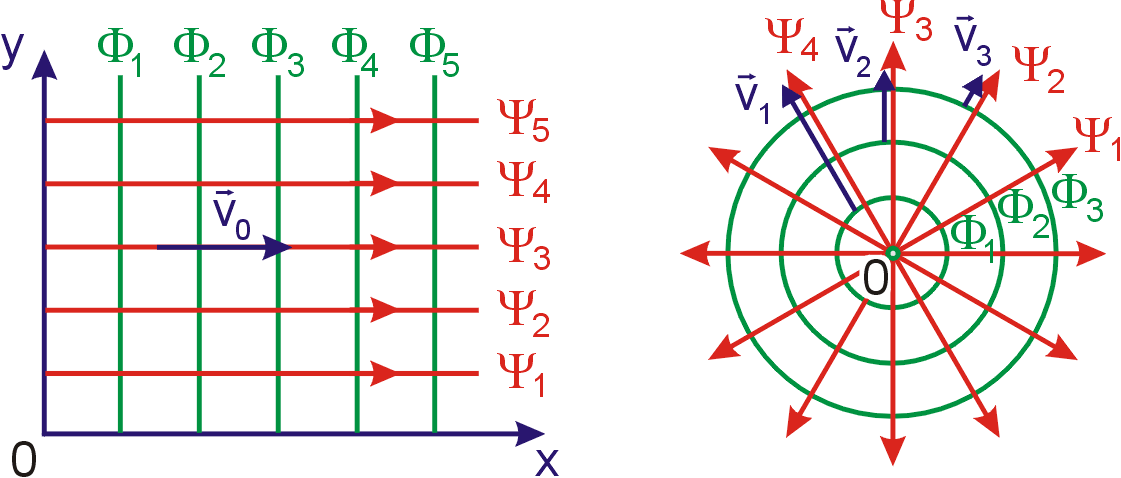
Zdroj nepatří do obrazu proudění, jaký jsme popisovali v čl.4.3. Není v něm splněna rovnice kontinuity proudění (viz stať 4.3.2), divergence rychlosti v místě zdroje je různá od nuly;
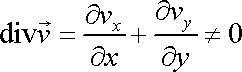 . . |
(4,173) |
Říkáme, že proudění má v místě zdroje singulární bod, který z popisu proudění podaného v čl.4.3 vyřazujeme.
Užití funkcí komplexní proměnné při řešení úloh rovinného proudění
Uvažujeme-li
potenciálové, tedy nevířivé proudění, musí vír rychlosti
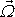 (4,48)
být roven nule. V rovinném
proudění v rovině x,y, které nyní vyšetřujeme, se podmínka
redukuje na požadavek, aby složka
(4,48)
být roven nule. V rovinném
proudění v rovině x,y, které nyní vyšetřujeme, se podmínka
redukuje na požadavek, aby složka
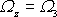 byla nulová, tedy
byla nulová, tedy
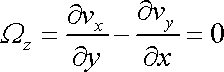 . . |
(4,174) |
Dále budeme předpokládat, že tekutina je nestlačitelná*). Pro takovou tekutinu platí rovnice kontinuity proudění v tvaru (4,65) , tedy
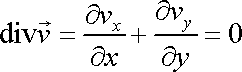 . . |
(4,175) |
Dosadíme-li do rovnice (4,175) za složky rychlosti jejich vyjádření dle rychlostního potenciálu (4,170) , dostáváme
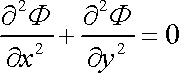 . . |
(4,176) |
Funkci, která splňuje podmínku
(4,176)
, říkáme harmonická
(viz např. [9],
čl.18.4). Tedy rychlostní potenciál
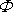 je při rovinném potenciálovém proudění
nestlačitelné tekutiny harmonickou funkcí. Podobně, dosadíme-li do rovnice
(4,174)
vyjádření složek rychlosti dle parciálních derivaci proudové funkce
je při rovinném potenciálovém proudění
nestlačitelné tekutiny harmonickou funkcí. Podobně, dosadíme-li do rovnice
(4,174)
vyjádření složek rychlosti dle parciálních derivaci proudové funkce
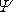 dané
rovnicemi
(4,169)
, zjistíme, že i proudová funkce je harmonickou funkcí, tedy
že platí
dané
rovnicemi
(4,169)
, zjistíme, že i proudová funkce je harmonickou funkcí, tedy
že platí
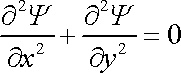 . . |
(4,177) |
Rovnice (4,176) , resp. (4,177) se nazývá Laplaceova rovnice.
Rychlostní potenciál
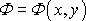 a proudová funkce
a proudová funkce
 popisující realizovatelné rovinné proudění
musí splňovat Laplaceovu rovnici a podmínky na okraji oblasti, v které
proudění probíhá. Musí tedy být v uvažované oblasti harmonickými funkcemi,
které splňují okrajové podmínky řešeného problému. Pro řešení problému stačí
stanovit jednu z obou funkcí, protože každá samostatně problém řeší a
vzájemně je lze přepočítat.
popisující realizovatelné rovinné proudění
musí splňovat Laplaceovu rovnici a podmínky na okraji oblasti, v které
proudění probíhá. Musí tedy být v uvažované oblasti harmonickými funkcemi,
které splňují okrajové podmínky řešeného problému. Pro řešení problému stačí
stanovit jednu z obou funkcí, protože každá samostatně problém řeší a
vzájemně je lze přepočítat.
Vzájemný vztah obou funkcí vyjadřují podmínky
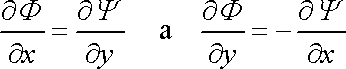 , , |
(4,178) |
které plynou z porovnání rovnic
(4,169)
a
(4,170)
.
Podmínky
(4,178)
se nazývají Cauchyovy--Riemanovy
podmínky. Pro funkce, které je splňují, se užívá označení sdružené funkce. Rychlostní
potenciál
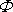 a proudová funkce
a proudová funkce
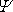 jsou tedy sdruženými funkcemi.
jsou tedy sdruženými funkcemi.
Vytvoříme-li z dvou harmonických funkcí
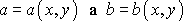 ,
které splňují Cauchyovy Riemanovy podmínky
,
které splňují Cauchyovy Riemanovy podmínky
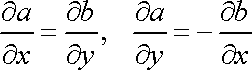 |
komplexní funkci
 tvaru
tvaru
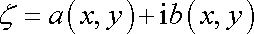 , , |
(4,179) |
bude tato funkce holomorfní neboli analytickou funkcí komplexní proměnné, tj. funkcí, která má v oblasti, kde jsou splněny shora uvedené podmínky, derivace všech řádů (viz např. [9], čl. 20.1). Podmínka, že funkce komplexní proměnné je analytickou funkcí, je silnou podmínkou, kterou lze pro řešení rovinných problémů mechaniky kontinua velmi dobře využít (viz např. [60]).
Analytickou funkci typu
(4,179)
vytvořenou
z rychlostního potenciálu
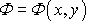 a proudové funkce
a proudové funkce
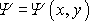 nazýváme komplexní potenciál proudění a budeme jej značit
nazýváme komplexní potenciál proudění a budeme jej značit
 .
Tedy pro komplexní funkci w
vyjadřující komplexní potenciál dostáváme
.
Tedy pro komplexní funkci w
vyjadřující komplexní potenciál dostáváme
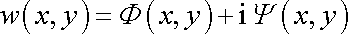 . . |
(4,180) |
Funkce
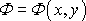 a
a
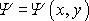 tvoří siť funkcí typu znázorněného na
obr.87, 88 nebo 84. Protože funkce jsou harmonické, splňují uvnitř oblasti
automaticky podmínky pro to, aby zobrazovaly realizovatelné rovinné proudění a
otázka najít řešení konkrétně zadaného problému se redukuje na nalezení
takového komplexního potenciálu w, který splňuje zadané okrajové
podmínky.
tvoří siť funkcí typu znázorněného na
obr.87, 88 nebo 84. Protože funkce jsou harmonické, splňují uvnitř oblasti
automaticky podmínky pro to, aby zobrazovaly realizovatelné rovinné proudění a
otázka najít řešení konkrétně zadaného problému se redukuje na nalezení
takového komplexního potenciálu w, který splňuje zadané okrajové
podmínky.
Protože o proudící tekutině
předpokládáme, že je ideální, mají okrajové podmínky na hraniční křivce oblasti
- stěně - standardní tvar. Hranice oblasti - stěna - je proudnicí a
ekvipotenciální křivka funkce
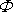 je k ní kolmá, tedy na stěně platí
je k ní kolmá, tedy na stěně platí
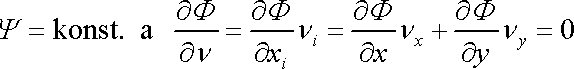 , , |
(4,181) |
kde symbolem
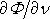 je označena derivace rychlostního potenciálu
dle normály k hraniční křivce oblasti. Symbol je v rovnici
(4,181)
dále rozepsán, aby se upřesnil jeho význam. Není-li oblast ohraničena hraniční
křivkou, tedy je-li neohraničená nebo hraniční křivka degeneruje
v singulární bod, okrajové podmínky jsou jiné, než udává rov.
(4,181)
.
je označena derivace rychlostního potenciálu
dle normály k hraniční křivce oblasti. Symbol je v rovnici
(4,181)
dále rozepsán, aby se upřesnil jeho význam. Není-li oblast ohraničena hraniční
křivkou, tedy je-li neohraničená nebo hraniční křivka degeneruje
v singulární bod, okrajové podmínky jsou jiné, než udává rov.
(4,181)
.
Hledat komplexní potenciál, který splňuje obecně zadané
okrajové podmínky, je úlohou, kterou lze analyticky řešit jen zřídka. Většinou
se musíme omezit na numerické aproximační metody (srov. odstavec o numerických
metodách ve stati I, 2.3.3 a v něm uvedenou literaturu), kterými určíme
buď funkci
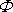 nebo
nebo
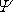 .
Význam zavedení komplexního potenciálu w
jako analytické (holomorfní) funkce komplexní proměnné z,
.
Význam zavedení komplexního potenciálu w
jako analytické (holomorfní) funkce komplexní proměnné z,
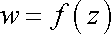 |
(4,182) |
tkví v tom, že každou analytickou funkci lze
interpretovat jako popis nějaké formy rovinného proudění nestlačitelné
tekutiny. Přesněji, protože sdružené funkce
 a
a
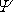 jsou vzájemně zaměnitelné, dostáváme
z každé analytické funkce
(4,182)
dvě formy proudění. Při řešení úloh
rovinného proudění postupujeme tedy obvykle inverzní metodou. Zadáme
analytickou funkci a hledáme jaké proudění popisuje. Z takto získané banky
řešení pak superpozicí sestavíme řešení problému, který nejblíže odpovídá
původně zadanému. Dále uvedeme několik příkladů.
jsou vzájemně zaměnitelné, dostáváme
z každé analytické funkce
(4,182)
dvě formy proudění. Při řešení úloh
rovinného proudění postupujeme tedy obvykle inverzní metodou. Zadáme
analytickou funkci a hledáme jaké proudění popisuje. Z takto získané banky
řešení pak superpozicí sestavíme řešení problému, který nejblíže odpovídá
původně zadanému. Dále uvedeme několik příkladů.
Rovnoměrné proudění znázorněné na obr.84 je popsáno analytickou funkcí
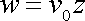 . . |
(4,183) |
Rozepíšeme-li rovnici (4,183)
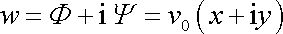 , , |
vidíme, že
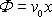 a
a
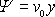 .
Proudnicemi
.
Proudnicemi
 jsou rovnoběžky s osou x
, ekvipotenciálními křivkami
jsou rovnoběžky s osou x
, ekvipotenciálními křivkami
 jsou rovnoběžky s osou y.
První složka gradientu rychlostního potenciálu (viz
(4,170)
) dává
jsou rovnoběžky s osou y.
První složka gradientu rychlostního potenciálu (viz
(4,170)
) dává
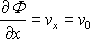 , a
tedy
, a
tedy
 je rychlost proudění ve směru osy x.
Komplexní potenciál tak opravdu popisuje proudění znázorněné na obr. 84.
je rychlost proudění ve směru osy x.
Komplexní potenciál tak opravdu popisuje proudění znázorněné na obr. 84.
Nyní ukážeme, jaké proudění popisuje analytická funkce
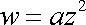 , , |
(4,184) |
kde a je reálná konstanta. Rozepsáním komplexního výrazu dostáváme
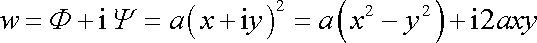 . . |
(4,185) |
Tedy ekvipotenciální křivky
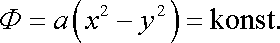 |
tvoří jednu soustavu rovnostranných hyperbol se souřadnicovými osami x, resp. y jako osami symetrie. Druhou soustavu hyperbol tvoří proudnice
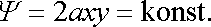 , , |
 přitom asymptoty hyperbol jedné soustavy jsou
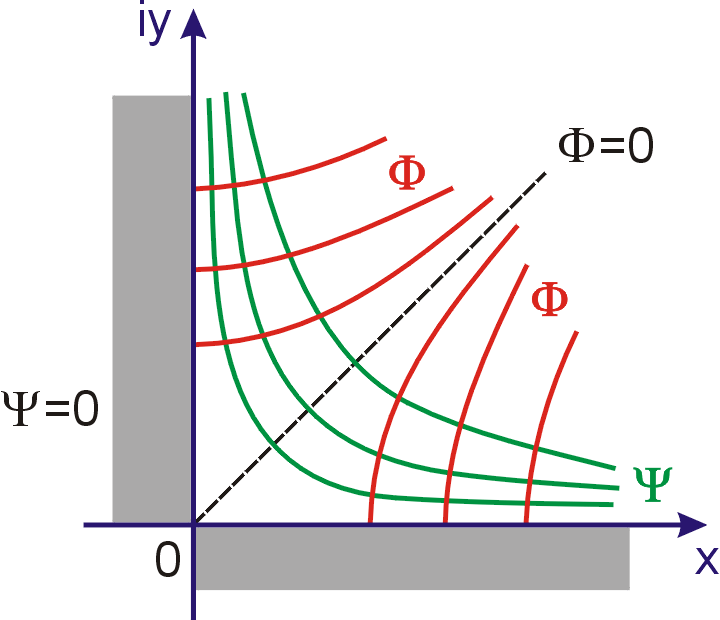
osami symetrie druhé soustavy hyperbol. Proudění popsané komplexním potenciálem
(4,185)
je znázorněno na obr. 89. Pro
přitom asymptoty hyperbol jedné soustavy jsou
osami symetrie druhé soustavy hyperbol. Proudění popsané komplexním potenciálem
(4,185)
je znázorněno na obr. 89. Pro
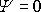 degeneruje hyperbola
degeneruje hyperbola
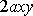 na vzájemně kolmé kladné úseky os x a y, které tvoří hraniční křivku (vzájemně
kolmé stěny) oblasti, v které probíhá proudění. Parciálním derivováním
rychlostního potenciálu
na vzájemně kolmé kladné úseky os x a y, které tvoří hraniční křivku (vzájemně
kolmé stěny) oblasti, v které probíhá proudění. Parciálním derivováním
rychlostního potenciálu
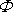 (viz
(4,170)
) dostáváme pro složky rychlosti
vyjádření
(viz
(4,170)
) dostáváme pro složky rychlosti
vyjádření
 .
Hraniční křivka oblasti tvoří proudnici, pro kterou konstantní hodnota proudové
funkce
.
Hraniční křivka oblasti tvoří proudnici, pro kterou konstantní hodnota proudové
funkce
 je nulová a rychlost, která v ose y míří k počátku soustavy souřadnic klesá
od nekonečné hodnoty své velikosti k nulové hodnotě v počátku, tj.
v bodu pravoúhlého zlomu proudnice. Od tohoto bodu rychlost změní směr a
s orientací shodnou s osou x
její velikost stoupá úměrně s hodnotou x, tj. od nuly do
nekonečna. Ekvipotenciální křivky jsou kolmé k hraniční proudnici, takže
obě okrajové podmínky
(4,181)
jsou splněny, i když pro ekvipotenciální
křivku
je nulová a rychlost, která v ose y míří k počátku soustavy souřadnic klesá
od nekonečné hodnoty své velikosti k nulové hodnotě v počátku, tj.
v bodu pravoúhlého zlomu proudnice. Od tohoto bodu rychlost změní směr a
s orientací shodnou s osou x
její velikost stoupá úměrně s hodnotou x, tj. od nuly do
nekonečna. Ekvipotenciální křivky jsou kolmé k hraniční proudnici, takže
obě okrajové podmínky
(4,181)
jsou splněny, i když pro ekvipotenciální
křivku
 jde o poněkud speciální případ, který však
je také přípustný. Komplexní potenciál
(4,184)
tedy popisuje rovinné potenciálové proudění
v čtvrtrovině ohraničené dvěmi navzájem kolmými stěnami. Poměrně
snadno lze najít komplexní potenciál i pro proudění ohraničené stěnami
svírajícími jiný úhel (viz např. [1] čl. 15.3).
jde o poněkud speciální případ, který však
je také přípustný. Komplexní potenciál
(4,184)
tedy popisuje rovinné potenciálové proudění
v čtvrtrovině ohraničené dvěmi navzájem kolmými stěnami. Poměrně
snadno lze najít komplexní potenciál i pro proudění ohraničené stěnami
svírajícími jiný úhel (viz např. [1] čl. 15.3).
Proudění znázorněné na obr.88, tedy radiální proudění zdroje v neomezeném prostoru lze vystihnout komplexním potenciálem
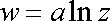 , , |
(4,186) |
kde a
je reálná konstanta. Je-li
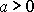 ,
je zdroj zřídlem, pro
,
je zdroj zřídlem, pro
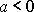 je zdroj propadem. Protože studovaný problém
je centrálně symetrický, je vhodné vyjádřit komplexní číslo z polárními souřadnicemi r,j ;
je zdroj propadem. Protože studovaný problém
je centrálně symetrický, je vhodné vyjádřit komplexní číslo z polárními souřadnicemi r,j ;
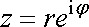 . . |
(4,187) |
Komplexní potenciál pak přepíšeme na tvar
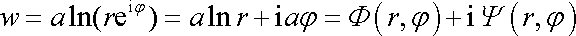 . . |
(4,188) |
Pro polární složky rychlosti tak dostáváme
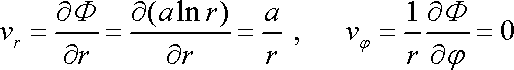 . . |
(4,189) |
Proudnice, tj. křivky
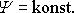 ,
jsou tedy radiální paprsky a ekvipotenciální křivky
,
jsou tedy radiální paprsky a ekvipotenciální křivky
 soustředné kružnice. Z rovnic
(4,189)
,
dále plyne, že velikost rychlosti je nepřímo úměrná vzdálenosti od zdroje,
soustředné kružnice. Z rovnic
(4,189)
,
dále plyne, že velikost rychlosti je nepřímo úměrná vzdálenosti od zdroje,
 .
Komplexní potenciál tedy dobře popisuje proudění znázorněné na obr.88. Navíc
ukazuje, že kdybychom chtěli lépe vystihnout kvantitativní poměry proudění a
kreslili ekvipotenciální křivky tak, aby rozdíly mezi hodnotami jejich konstant
byly stálé, vzdálenosti mezi koncentrickými kružnicemi ekvipotenciálních křivek
by byly nepřímo úměrné r. Podmínka
.
Komplexní potenciál tedy dobře popisuje proudění znázorněné na obr.88. Navíc
ukazuje, že kdybychom chtěli lépe vystihnout kvantitativní poměry proudění a
kreslili ekvipotenciální křivky tak, aby rozdíly mezi hodnotami jejich konstant
byly stálé, vzdálenosti mezi koncentrickými kružnicemi ekvipotenciálních křivek
by byly nepřímo úměrné r. Podmínka
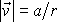 je totiž nutnou podmínkou pro to, aby obr.
88 opravdu popisoval potenciálové proudění.
je totiž nutnou podmínkou pro to, aby obr.
88 opravdu popisoval potenciálové proudění.
V počátku, kde je umístěn zdroj, je rychlost proudění nekonečná, není tam splněna rovnice kontinuity proudění, ani další podmínky potenciálového rovinného proudění, např. Cauchyovy-Riemanovy podmínky. Ani komplexní potenciál (4,186) nemá v tomto bodě konečnou derivaci. Takový bod označujeme za singulární bod, u funkce (4,186) mluvíme o logaritmické singularitě. Singulární body z obrazu proudění vyjímáme a uvažujeme jen o proudění mimo ně. Tak např. můžeme určit mohutnost zdroje m jako tok vektoru rychlosti ekvipotencíální křivkou obklopující zdroj
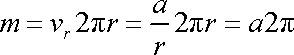 . . |
(4,190) |
Protože mimo singulární bod již platí rovnice kontinuity, je jedno, přes kterou ekvipotenciální křivku tok počítáme.
Vyšetřujeme-li pole zřídla a propadu stejné mohutnosti,
dostaneme pole analogické elektrostatickému poli stejně velkého kladného a
záporného náboje. V elektrickém poli takové pole označujeme jako pole
dipólu, přičemž jako moment dipólu označujeme vektorovou veličinu
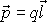 ,
kde q je velikost nábojů a
,
kde q je velikost nábojů a
 je vektor, jehož velikost je rovna
vzdálenosti obou nábojů a který je orientován od záporného náboje ke kladnému.
Ve velkých vzdálenostech od obou nábojů pole již téměř nezávisí na jejich
vzdálenosti, ale pouze na momentu dipólu. Proto se zavádí elementární dipól,
jako dipól, který vznikne, když oba náboje limitně přiblížíme tak, že se
dostanou do jednoho bodu, přičemž moment dipólu zůstane zachován. Pole
elementárního dipólu v místě o polohovém vektoru
je vektor, jehož velikost je rovna
vzdálenosti obou nábojů a který je orientován od záporného náboje ke kladnému.
Ve velkých vzdálenostech od obou nábojů pole již téměř nezávisí na jejich
vzdálenosti, ale pouze na momentu dipólu. Proto se zavádí elementární dipól,
jako dipól, který vznikne, když oba náboje limitně přiblížíme tak, že se
dostanou do jednoho bodu, přičemž moment dipólu zůstane zachován. Pole
elementárního dipólu v místě o polohovém vektoru
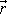 pak závisí pouze na velikosti dipólového
momentu a vzájemné orientaci vektorů
pak závisí pouze na velikosti dipólového
momentu a vzájemné orientaci vektorů
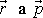 .
.
Pole zřídla a propadu stejné mohutnosti m nazýváme dubletem. Označíme-li vektor mířící od propadu ke zdroji
symbolem
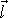 ,
můžeme v analogii s momentem dipólu zavést moment dubletu
,
můžeme v analogii s momentem dipólu zavést moment dubletu
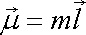 . . |
(4,191) |
Posuneme-li v limitě zdroj i propad do jednoho bodu při
zachování momentu dubletu
 (délka
l v limitě dosáhne hodnoty nula, mohutnost m roste do nekonečna, ale hodnota jejich
součinu m
= ml zůstává v celém limitním
postupu zachována), získáme v tomto bodě elementární dublet, který je
charakterizován velikostí a směrem momentu dubletu
(délka
l v limitě dosáhne hodnoty nula, mohutnost m roste do nekonečna, ale hodnota jejich
součinu m
= ml zůstává v celém limitním
postupu zachována), získáme v tomto bodě elementární dublet, který je
charakterizován velikostí a směrem momentu dubletu
 .
Komplexní potenciál rovinného*) elementárního dubletu, jehož moment je
orientován ve směru kladné osy x , je dán výrazem
.
Komplexní potenciál rovinného*) elementárního dubletu, jehož moment je
orientován ve směru kladné osy x , je dán výrazem
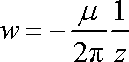 . . |
(4,192) |
Úpravou tohoto výrazu dostáváme
 . . |
(4,193) |
Porovnáním s obecným tvarem komplexního potenciálu
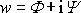 dostáváme pro rychlostní potenciál
dostáváme pro rychlostní potenciál
 a
proudovou funkci
a
proudovou funkci
 elementárního rovinného dubletu tato
vyjádření:
elementárního rovinného dubletu tato
vyjádření:
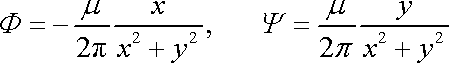 . . |
(4,194) |
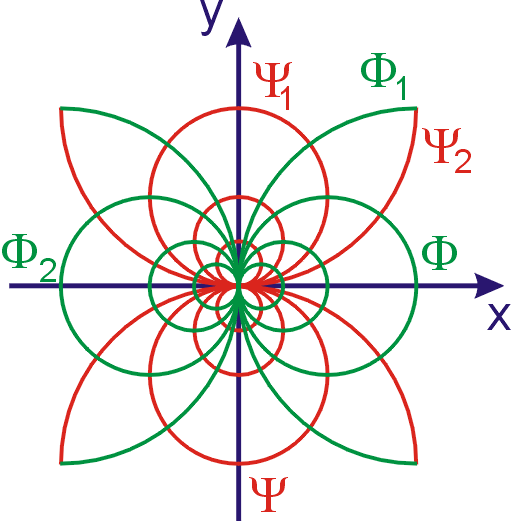 Proudění
elementárního dubletu je znázorněno na obr.90. Ekvipotenciální křivky
Proudění
elementárního dubletu je znázorněno na obr.90. Ekvipotenciální křivky
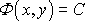 i proudnice
i proudnice
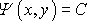 jsou kružnice, které se protínají kolmo (musí
být splněny podmínky
(4,178)
). Hodnoty konstant křivek stálé hodnoty jsme
označili C . Středy kružnic ekvipotenciálních křivek leží na ose x
, všechny se dotýkají v počátku soustavy souřadnic, kružnice se středem na
kladné části osy mají C < 0 , ty, jejichž středy
leží na záporné části osy, mají C > 0 a osa
y , která je ekvipotenciální
křivkou se středem v nekonečnu, má
C = 0. Kružnice proudnic mají
středy na ose y , pro kružnice, jejichž středy jsou na kladné ose y , nyní platí C >
0, pro kružnice se středy na záporné ose
y máme C <
0 a osa x má C = 0. Pro složky rychlosti dostáváme
z rychlostního potenciálu
jsou kružnice, které se protínají kolmo (musí
být splněny podmínky
(4,178)
). Hodnoty konstant křivek stálé hodnoty jsme
označili C . Středy kružnic ekvipotenciálních křivek leží na ose x
, všechny se dotýkají v počátku soustavy souřadnic, kružnice se středem na
kladné části osy mají C < 0 , ty, jejichž středy
leží na záporné části osy, mají C > 0 a osa
y , která je ekvipotenciální
křivkou se středem v nekonečnu, má
C = 0. Kružnice proudnic mají
středy na ose y , pro kružnice, jejichž středy jsou na kladné ose y , nyní platí C >
0, pro kružnice se středy na záporné ose
y máme C <
0 a osa x má C = 0. Pro složky rychlosti dostáváme
z rychlostního potenciálu
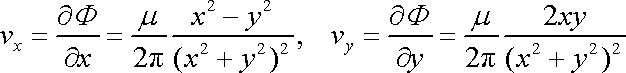 . . |
(4,195) |
Rychlost
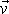 je zřejmě v počátku soustavy souřadnic
nekonečná, počátek je singulárním bodem, komplexní potenciál
(4,192)
tedy
regulárně popisuje proudění elementárního dubletu v celé rovině
s výjimkou počátku.
je zřejmě v počátku soustavy souřadnic
nekonečná, počátek je singulárním bodem, komplexní potenciál
(4,192)
tedy
regulárně popisuje proudění elementárního dubletu v celé rovině
s výjimkou počátku.
Vyšetříme nyní proudění vyjádřené komplexním potenciálem
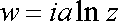 , , |
(4,196) |
tedy potenciálem, který vznikne z potenciálu (4,178) jeho vynásobením imaginární jednotkou i. Vynásobíme-li obecné vyjádření komplexního potenciálu (4,180) imaginární jednotkou, dostaneme komplexní potenciál
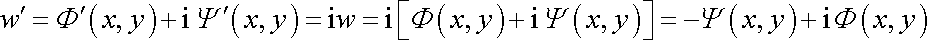 . . |
(4,197) |
Z rovnice
(4,197)
plyne, že siť znázorňující obraz
proudění se nezmění, pouze sdružené funkce
 si vymění své úlohy;
si vymění své úlohy;
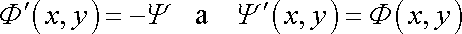 , , |
(4,198) |
Proudová funkce potenciálu
w se stane až na znaménko rychlostním potenciálem funkce
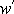 a rychlostní potenciál funkce w se stane proudovou funkcí komplexního
potenciálu
a rychlostní potenciál funkce w se stane proudovou funkcí komplexního
potenciálu
 .
Změna znaménka v první rovnici
(4,198)
nemá vliv na tvar křivek stálé
hodnoty funkcí, pouze konstantám C
kótujícím ekvipotenciální křivky komplexního potenciálu
.
Změna znaménka v první rovnici
(4,198)
nemá vliv na tvar křivek stálé
hodnoty funkcí, pouze konstantám C
kótujícím ekvipotenciální křivky komplexního potenciálu
 musíme dát v jejich nové roli, kdy
znázorňují proudnice komplexního potenciálu
w , opačné znaménko.
musíme dát v jejich nové roli, kdy
znázorňují proudnice komplexního potenciálu
w , opačné znaménko.
 Obrázek
88, prohodí-li se role ekvipotenciálních křivek a proudnic, znázorňuje i
proudění popsané komplexním potenciálem
(4,196)
, které označujeme jako proudění potenciálového víru. Protože
budeme proudění
(4,196)
nyní podrobně probírat, překreslíme obrázek 88 a kromě
prohození označení křivek stálých hodnot na něm vyznačíme rychlosti proudění na
jednotlivých proudnicích., Překreslený obrázek znázorňující proudění
potenciálového víru je zařazen pod číslem 91.
Obrázek
88, prohodí-li se role ekvipotenciálních křivek a proudnic, znázorňuje i
proudění popsané komplexním potenciálem
(4,196)
, které označujeme jako proudění potenciálového víru. Protože
budeme proudění
(4,196)
nyní podrobně probírat, překreslíme obrázek 88 a kromě
prohození označení křivek stálých hodnot na něm vyznačíme rychlosti proudění na
jednotlivých proudnicích., Překreslený obrázek znázorňující proudění
potenciálového víru je zařazen pod číslem 91.
Aplikujeme-li pravidlo (4,198) na vztah mezi radiálním prouděním zdroje (4,186) a prouděním potenciálového víru (4,196) , resp. (4,197) , dostáváme pro rychlostní potenciál a proudovou funkci potenciálového víru tato vyjádření v polárních souřadnicích r,j :
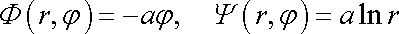 . . |
(4,199) |
Z nich pro složky rychlosti plyne
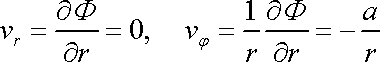 . . |
(4,200) |
Vypočteme-li cirkulaci rychlosti (4,162) podél kterékoliv proudnice, zjistíme, že má nenulovou hodnotu
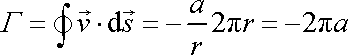 . . |
(4,201) |
Intenzita víru
(4,163)
rovná cirkulaci
(4,201)
je tedy
nenulová a uvnitř proudnice musí někde být nenulový vír rychlosti
 . Protože uvedený závěr platí pro všechny
proudnice, může se nenulový vír
. Protože uvedený závěr platí pro všechny
proudnice, může se nenulový vír
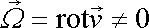 |
(4,202) |
nacházet jedině v počátku souřadnicové soustavy, a jelikož uvažujeme rovinné proudění, prochází počátkem kolmo k sledované rovině a musí být nekonečně veliký, aby jeho tok plochou libovolné proudnice (4,163) mohl být roven konečné hodnotě cirkulace (4,201) . Počátkem tedy prochází kolmo k rovině izolovaná vírová čára, pro kterou součin nekonečně velké hodnoty víru rychlosti a nulové plochy průřezu dá konečnou hodnotu intenzity víru. V rovinném vyjadřování hovoříme o vírovém bodu s intenzitou víru rovnou cirkulaci (4,201) ;
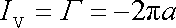 . . |
(4,203) |
Protože je rotace rychlosti různá od nuly,
 ,
není právě popisované proudění prouděním potenciálovým. Relace
,
není právě popisované proudění prouděním potenciálovým. Relace
 však platí v jediném bodě, v počátku
souřadnicové soustavy, stačí tedy tento singulární bod z popisu proudění
vyjmout a ve zbytku prostoru bude podmínka potenciálového proudění splněna.
však platí v jediném bodě, v počátku
souřadnicové soustavy, stačí tedy tento singulární bod z popisu proudění
vyjmout a ve zbytku prostoru bude podmínka potenciálového proudění splněna.
Oblast, v které je podmínka splněna, však již není
jednoduše souvislou oblastí, ale dvojnásobně souvislou oblastí (viz např. [9], čl.
22.1). Při uvažování o potenciálu musíme vždy zůstat uvnitř této oblasti, např.
počítáme-li podle nějaké uzavřené křivky cirkulaci rychlosti
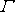 , nesmí tato křivka obsahovat počátek,
abychom dostali výsledek, který odpovídá potenciálovému proudění, tedy nulovou
cirkulaci. V této dvojnásobně souvislé oblasti má smysl uvažovat
potenciálový vír
(4,196)
jako opravdový potenciál, a tím je vysvětlen zdánlivý
rozpor zmíněný v úvodu stati 4.7.1.
, nesmí tato křivka obsahovat počátek,
abychom dostali výsledek, který odpovídá potenciálovému proudění, tedy nulovou
cirkulaci. V této dvojnásobně souvislé oblasti má smysl uvažovat
potenciálový vír
(4,196)
jako opravdový potenciál, a tím je vysvětlen zdánlivý
rozpor zmíněný v úvodu stati 4.7.1.
Zavedeme-li do komplexního potenciálu
(4,196)
vyjádření
konstanty a dle cirkulace
rychlosti
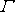 dané rovnicí
(4,201)
, dostaneme pro
potenciálový vír komplexní vyjádření
dané rovnicí
(4,201)
, dostaneme pro
potenciálový vír komplexní vyjádření
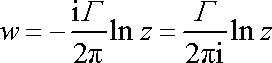 |
(4,204) |
a pro jeho rychlostní potenciál vyjádření
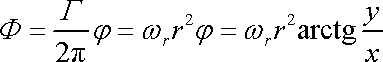 . . |
(4,205) |
Do rovnice
(4,205)
jsme zavedli úhlovou rychlost
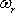 pohybu částice po proudnici
s poloměrem r; úhlová rychlost podobně jako postupná rychlost je nepřímo úměrná
poloměru. Rychlostní potenciál tvaru
(4,205)
je posledním členem rychlostního
potenciálu
(4,148)
obtékaného rotujícího válce, který jsme užili při odvození
Magnusovy síly ve stati 4.6.5. Úhlová rychlost rotace znázorněná na obr.80 je
záporná. Další dva členy potenciálu
(4,148)
jsou rychlostní potenciál
rovnoměrného proudění
(4,183)
pohybu částice po proudnici
s poloměrem r; úhlová rychlost podobně jako postupná rychlost je nepřímo úměrná
poloměru. Rychlostní potenciál tvaru
(4,205)
je posledním členem rychlostního
potenciálu
(4,148)
obtékaného rotujícího válce, který jsme užili při odvození
Magnusovy síly ve stati 4.6.5. Úhlová rychlost rotace znázorněná na obr.80 je
záporná. Další dva členy potenciálu
(4,148)
jsou rychlostní potenciál
rovnoměrného proudění
(4,183)
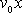 a rychlostní potenciál elementárního dubletu
(4,193)
, jehož moment
a rychlostní potenciál elementárního dubletu
(4,193)
, jehož moment
 o velikosti
o velikosti
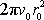 byl orientován proti směru x,
a proto
byl orientován proti směru x,
a proto
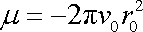 . . |
(4,206) |
Rychlostní potenciál
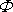 pro řešení problému obtékání rotujícího
válce byl tedy sestaven ze tří složek tak, aby byly splněny okrajové podmínky.
Tyto podmínky jsou dvě. První říká, že rychlost v nekonečnu je orientována
ve směru kladné osy x
a má velikost
pro řešení problému obtékání rotujícího
válce byl tedy sestaven ze tří složek tak, aby byly splněny okrajové podmínky.
Tyto podmínky jsou dvě. První říká, že rychlost v nekonečnu je orientována
ve směru kladné osy x
a má velikost
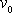 .
Druhá, že kružnice, v které válec protíná sledovanou rovinu, je proudnicí,
tedy že na kružnici musí být hodnota proudové funkce konstantní,
.
Druhá, že kružnice, v které válec protíná sledovanou rovinu, je proudnicí,
tedy že na kružnici musí být hodnota proudové funkce konstantní,
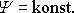 .
.
Ve stati 4.6.5 je problém popsán rychlostním
potenciálem
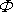 , druhá okrajová podmínka je formulována pro
proudovou funkci
, druhá okrajová podmínka je formulována pro
proudovou funkci
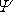 .
To však nečiní žádné potíže, protože z předchozího výkladu v této
stati plyne, že funkce
.
To však nečiní žádné potíže, protože z předchozího výkladu v této
stati plyne, že funkce
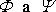 jsou sdružené (viz
(4,178)
) a komplexní
potenciál w je z nich sestaven
(viz
(4,180)
). Všechny tři funkce jsou tak vzájemně přepočitatelné a každá
z nich samostatně problém rovinného potenciálového proudění plně řeší.
jsou sdružené (viz
(4,178)
) a komplexní
potenciál w je z nich sestaven
(viz
(4,180)
). Všechny tři funkce jsou tak vzájemně přepočitatelné a každá
z nich samostatně problém rovinného potenciálového proudění plně řeší.
Nekoná-li válec rotaci, stačí k popisu proudění
kombinace prvých dvou členů rychlostního potenciálu
(4,148)
. V třetím
členu, který je dán výrazem rozepsaným v
(4,205)
, můžeme hodnotu úhlové
rychlosti w
, resp. cirkulace
 volit, aniž tím porušíme skutečnost, že
kružnice reprezentující válec v rovině je proudnicí. Volbou se pouze změní
stupeň asymetrie obrazu proudění vzhledem k ose x , a tím i velikost
Magnusovy síly
(4,152)
. Pro problém obtékání křídla (stať 4.6.6) tuto libovůli
v stanovení cirkulace omezíme požadavkem konečné rychlosti u hrany křídla
(viz úvahy na konci stati 4,6,6), abychom pro křídlo, kde nastavitelný parametr
podobný rychlosti rotace válce nemáme, získali reálnou hodnotu vztlaku závislou
pouze na tvaru křídla.
volit, aniž tím porušíme skutečnost, že
kružnice reprezentující válec v rovině je proudnicí. Volbou se pouze změní
stupeň asymetrie obrazu proudění vzhledem k ose x , a tím i velikost
Magnusovy síly
(4,152)
. Pro problém obtékání křídla (stať 4.6.6) tuto libovůli
v stanovení cirkulace omezíme požadavkem konečné rychlosti u hrany křídla
(viz úvahy na konci stati 4,6,6), abychom pro křídlo, kde nastavitelný parametr
podobný rychlosti rotace válce nemáme, získali reálnou hodnotu vztlaku závislou
pouze na tvaru křídla.
Skládání (superpozice) různých standardních potenciálů ke splnění okrajových podmínek složitěji zadaných problémů proudění je jedním ze způsobů, jak lze umocnit možnosti výše uvedených metod řešení problémů rovinného proudění. Při tomto skládání musí být zvýšená pozornost věnována singulárním bodům. V případě obtékání kruhového rotujícího válce jsou všechny singulární body rychlostního potenciálu (4,148) v počátku souřadnicové soustavy, který se nachází ve středu kružnice reprezentující válec, tedy mimo oblast (vnějšek kružnice), v které potenciálem proudění popisujeme. Podrobněji je obtékání kruhového válce rozebráno v [1], čl.15.4.
Konformní zobrazení
Dalším způsobem jak rozšířit možnosti řešení problémů rovinného potenciálového proudění na případy, kdy okrajové podmínky jsou složitější, je metoda konformního zobrazení. Kvalitativně jsme se o metodě již zmínili ve stati 4.6.6, když jsme uvedli, že metodou lze převést výsledky získané pro obtékání rotujícího válce (stať 4.6.5) na obtékání křídla. Jmenovitě jsme uvedli, že výraz pro výpočet Magnusovy síly (4,152) lze užít i pro výpočet vztlaku křídla (4,157) , když se vhodně zvolí nastavitelné konstanty. Na obr.84 jsme ukázali, jak se zobrazením převede proudění v okolí rotujícího válce na proudění v okolí schematizovaného křídla. Nyní metodu blíže objasníme.
Výše v této stati jsme si ukázali, že nalezneme-li
komplexní potenciál
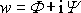 vyhovující okrajovým podmínkám zadaného
problému rovinného potenciálového proudění, máme problém vyřešen. To, co bylo
řečeno o komplexním potenciálu, platí i pro funkce
vyhovující okrajovým podmínkám zadaného
problému rovinného potenciálového proudění, máme problém vyřešen. To, co bylo
řečeno o komplexním potenciálu, platí i pro funkce
 (rychlostní potenciál) a
(rychlostní potenciál) a
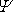 (proudová funkce), které jej vytvářejí.
Podaří-li se nám tedy najít takové zobrazení
(proudová funkce), které jej vytvářejí.
Podaří-li se nám tedy najít takové zobrazení
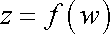 , , |
(4,207) |
které převede okrajové podmínky komplexního potenciálu w na okrajové podmínky dosud nevyřešeného problému, aniž se zobrazením poruší holomorfnost (analytičnost) funkce, bude komplexní funkce z komplexním potenciálem dosud nevyřešeného problému. Známe-li však komplexní potenciál problému splňující okrajové podmínky, známe řešení problému a dosud nevyřešený problém je vyřešen. Toto je idea metody konformního zobrazení. K jejímu přesnému použití je zapotřebí dodržet některé další podmínky, které jsou uvedeny např. v [1], čl.15.5.
Analytičnost komplexního potenciálu bude zachována, bude-li
funkce
 zprostředkující zobrazení
(4,207)
analytickou funkcí, tj. bude-li mít ve všech bodech oblasti, kterou zobrazuje,
derivaci. Existence nenulové derivace komplexní funkce znamená, že dvě křivky,
které se v rovině w
(rovina předmětová) protínají pod úhlem
a , budou se
v rovině z (obrazová rovina)
protínat pod stejným úhlem a. Zobrazení, které splňuje tuto vlastnost, se nazývá
konformním. Tedy zobrazení
(4,207)
zprostředkované analytickou (holomorfní)
funkcí je konformním zobrazením.
zprostředkující zobrazení
(4,207)
analytickou funkcí, tj. bude-li mít ve všech bodech oblasti, kterou zobrazuje,
derivaci. Existence nenulové derivace komplexní funkce znamená, že dvě křivky,
které se v rovině w
(rovina předmětová) protínají pod úhlem
a , budou se
v rovině z (obrazová rovina)
protínat pod stejným úhlem a. Zobrazení, které splňuje tuto vlastnost, se nazývá
konformním. Tedy zobrazení
(4,207)
zprostředkované analytickou (holomorfní)
funkcí je konformním zobrazením.
Obvyklou okrajovou podmínkou je, že okraj oblasti je proudnicí. Úkol najít vhodné konformní zobrazení oblasti ze známým komplexním potenciálem na oblast, kde komplexní potenciál hledáme, se pak redukuje na úkol najít konformní zobrazení, které převádí okrajovou křivku známého řešení na okrajovou křivku hledaného řešení. Při vyšetřování vztlaku křídla ve stati 4.6.6. se tak hledá konformní zobrazení kružnice reprezentující okrajovou křivku rotujícího válce na tvar přibližně vystihující profil křídla (viz obr.83). Hledané konformní zobrazení je Žukovského transformace (4,154) , kterou zde přepíšeme v tvaru odpovídajícím rov. (4,207)
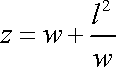 . . |
(4,208) |
Přitom střed kružnice reprezentující rotující válec, pro nějž známe komplexní potenciál w , nemůžeme umístit do počátku souřadnicové soustavy, ale musíme jej posunout do bodu naznačeného na obr.83, aby zobrazením (4,208) kružnici odpovídalo schematizované křídlo. Znamená to, že před konformním zobrazením musíme známý komplexní potenciál w rotujícího válce, obvykle vyjádřený pro počátek soustavy souřadnic (komplexní potenciál odpovídající rychlostnímu potenciálu (4,148) ), transformovat na tvar odpovídající novému středu kružnice. Jakmile se pak transformace kružnice na "křídlo" povede, je již tím, že funkce z a w jsou analytické, zaručeno, že vně "křídla" bude funkce z popisovat správně rovinné potenciálové obtékání "křídla" nestlačitelnou ideální tekutinou.
Vypočteme-li derivaci funkce z,
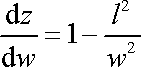 , , |
(4,209) |
zjistíme, že v bodech
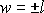 je derivace nulová. Nulová hodnota derivace
nezaručuje konformnost zobrazení. Jak se tyto singularity v uvažovaném
konformním zobrazení překonají a upřesnění dalších zde naznačených postupů lze
nalézt v již citovaném článku.15.5 z [1], Podrobně se metodou
konformního zobrazení se zaměřením na problémy rovinné pružnosti zabývá kniha [60].
je derivace nulová. Nulová hodnota derivace
nezaručuje konformnost zobrazení. Jak se tyto singularity v uvažovaném
konformním zobrazení překonají a upřesnění dalších zde naznačených postupů lze
nalézt v již citovaném článku.15.5 z [1], Podrobně se metodou
konformního zobrazení se zaměřením na problémy rovinné pružnosti zabývá kniha [60].
Hydraulika je technická nauka, která se zabývá aplikací zákonů mechaniky tekutin při řešení praktických úkolů tečení kapalin a plynů. Zákony mechaniky tekutin užívá v co nejjednodušší formě a doplňuje je praktickými experimentálně zjištěnými poznatky nezbytnými pro řešení konkrétních úloh. Výsledky hydraulických výzkumů se před jejich aplikacemi prověřují a upřesňují důkladnými laboratorními a provozními zkouškami.
V hydraulice se zkoumá proudění kapalin a plynů. Vycházíme přitom z Bernoulliovy rovnice (4,84) a rovnice kontinuity (4,52) . Uvažujeme je obvykle v nejjednodušších tvarech a jako rovnice platné pro průměrné hodnoty v jednotlivých průřezech trubice či koryta. Plyny uvažujeme jen do takových tlaků, kde můžeme změny jejich hustoty při proudění zanedbat a užívat Bernoulliovu rovnici v tvaru (4,91) a rovnici kontinuity v tvaru (4,53) .
Popis proudění viskózních tekutin nevychází v hydraulice z Navierových-Stokesových rovnic, ale z Bernoulliovy rovnice. Vystižení energetických ztrát při proudění viskózních tekutin trubicemi a koryty se provádí zavedením pojmu hydrodynamický odpor potrubí či koryta. Bernoulliova rovnice se doplňuje o veličinu zvanou ztrátová výška (podrobněji viz 4.7.4).
Uvedená omezení hydrauliky se vztahují k jejím klasickým formám. V poslední době vychází hydraulika při řešení stále složitějších případů technicky důležitých proudění ze všech dostupných závěrů teoretické mechaniky tekutin. Specifikou hydrauliky pak zůstává nutnost doplnění problematiky o zahrnutí i těch podmínek proudění, které dosud nejsou plně teoreticky zpracovány, a. nezbytnost důkladného experimentálního prověření výsledků.
*) Vyhovovalo by i vyjádření s opačně orientovaným gradientem, tj. s prohozenými znaménky složek, neboť orientace růstu proudové funkce není jejím zadáním určena. V dalším se přidržíme volby znamének dle rovnice (4,169) .
*) Omezujeme se tak na kapaliny a na poměrně častý případ proudění plynů, kdy změny jejich hustoty při proudění můžeme zanedbat. Mezi takové případy patří i proudění vyšetřovaná ve statích 4.6.5 a 4.6.6.
*) Rovinný dublet se od prostorového podstatně liší např. jinou mocninou závislostí ubývání potenciálu se vzdáleností od středu dipólu. Proto nelze ani hledat přesné analogie mezi potenciálem elektrického elementárního dipólu, který vyšetřujeme obvykle v prostoru, a dále rozebíraného potenciálu rovinného elementárního dubletu.
Hlavní obory hydrauliky:
. tečení v potrubí a potrubní rozvody,
Při hydraulickém zkoumání potrubí a potrubních rozvodů se především sledují otázky jejich kapacity a výkonnosti. Navrhují se např. městské rozvody vody a plynu nebo dálkové rozvody vody, plynu a nafty. Znamená to určit optimální průměry potrubí, nezbytné výkonnosti čerpadel, odolnost potrubí proti vibracím a rázům, které v nich mohou vznikat apod. U dálkových rozvodů se zkoumají i otázky možného snížení hydrodynamického odporu (viskozity) přidáním různých příměsí do transportovaných látek. Snížení odporu přináší úspory na dopravních nákladech. Základní otázky této problematiky probereme v stati 4.7.4.
Při výzkumu proudění tekutin je také nutno zjišťovat, jakými silami tekutina působí na své okolí. Sem spadá např. otázka, jak nejlépe převést energii tekutiny na pohon strojů, tedy otázky konstrukce vodních kol a turbín. Dále pak zkoumání, jak proudící tekutina působí na potrubí, kterým je vedena nebo jak řeka vymílá své břehy a usazuje nánosy ve svém okolí. Ve stati 4.7.5 si uvážením změn hybnosti proudící tekutiny objasníme některé základní otázky této problematiky, např. to, proč je zapotřebí značné síly k ovládání hasičské stříkačky, kterou posíláme proud vody na oheň. Jak se při letošních povodních (rok 2002) ukázalo, jsou velmi důležité otázky hydrologockých a ekologických úprav vodních toků. Tyto otázky jsou již mimo zaměření našeho textu a probírány nebudou..
Trysky, otvory a různé výpustě se konstruují tak, aby co nejlépe vyhovovaly svému účelu, výtok byl co nejhladší a zařízení byla co nejméně opotřebovávána. Opět zde k čisté hydrodynamice přistupují další obory, které je nutné respektovat, např. nauka o materiálech, která nám umožní najít vhodný materiál pro navrhované prvky. U trysek je často třeba zvolit tvar, který umožňuje co nejrychlejší výtok tekutiny. Je možné navrhovat i systémy, které upravují cestu tryskajícího paprsku, např. přepínají paprsek mezi dvěma různými směry. Zde k zákonům hydrodynamiky přistupují úvahy o povrchovém napětí (kapilárních silách). Některé otázky výtoku tekutiny probereme ve stati 4.7.6.
Tečení pórovitými materiály se zkoumá jednak v souvislosti s pohyby tzv. spodních vod, jednak s problematikou filtrování. Znalost pohybu vody v zemi je důležitá např. pro zakládání staveb. Při filtrování je úkolem najít optimální poměr mezi kvalitou oddělení součástí, dobou trvání procesu a jeho energetickou náročností. Podrobnější seznámení s těmito a dalšími hydraulickými problémy najde čtenář např. v [62], [63].
Prouděním
reálné tekutiny trubicí jsme se již zabývali ve stati 4.4.1. Tam jsme se však
omezili na laminární proudění. Pro případ, kdy tekutina je newtonovská, jsme
odvodili Poiseuillův zákon
(4,127)
, který jsme pro nenewtonovské tekutiny
s rovnicí toku
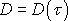 zobecnili na tvar daný rovnicí
(4,132)
. Ve
stati 4.4.1 jsme se z tekutin omezili na kapaliny. V hydraulice
uvažujeme jen nestlačitelné plyny, a pro ty platí stejné rovnice jako pro
kapaliny, a proto dále v tomto článku budeme objekt našeho zájmu označovat
jako tekutinu, abychom nestlačitelné plyny z úvah nevyřazovali.
zobecnili na tvar daný rovnicí
(4,132)
. Ve
stati 4.4.1 jsme se z tekutin omezili na kapaliny. V hydraulice
uvažujeme jen nestlačitelné plyny, a pro ty platí stejné rovnice jako pro
kapaliny, a proto dále v tomto článku budeme objekt našeho zájmu označovat
jako tekutinu, abychom nestlačitelné plyny z úvah nevyřazovali.
Omezení
na laminární proudění je pro hydrauliku nepřijatelné. Většina tekutin
dopravovaných potrubími (především voda, nafta, topný plyn) v nich teče
turbulentně. Stanovíme-li např. Reynoldsovo číslo
(4,137)
pro vodu teploty
okolo 20oC (kinematická viskozita
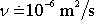 ), která protéká rychlostí
), která protéká rychlostí
 potrubím kruhového průřezu o poloměru R
= 0,1 m, dostaneme,
potrubím kruhového průřezu o poloměru R
= 0,1 m, dostaneme,
 , , |
což jest hodnota jasně spadající do oblasti turbulentního proudění (srov. text za rovnicí (4,138) ). Přitom uvedené hodnoty rychlosti proudění a poloměru trubky se při rozvodu vody běžně vyskytují.
V textu za obr.75 jsme odvodili Bernoulliovu rovnici z předpokladu, že práce vykonaná na tekutinu v proudové trubici způsobí zvýšení její kinetické energie (viz rov. (4,94) )
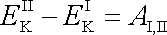 . . |
(4,94) |
Přitom práce AI,II se rovná úbytku potenciální energie zvětšenému o práci VDp , kterou vykoná okolní tekutina, když rozdílem tlaků Dp posune tekutinu z pozice I do pozice II. Symbolem V je označen objem posunuté tekutiny. Protože se jedná o ideální tekutinu, nepočítáme s žádnou disipací (rozptýlením) energie a z uvažované úvahy získáme Bernoulliovu rovnici v tvaru (4,91)
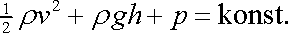 |
(4,91) |
Při odvození Poiseuillova zákona (viz stať 4.4.1) uvažujeme proudění vodorovnou trubicí, mezi jejímiž konci je rozdíl tlaku Dp a předpokládáme, že na obou koncích trubice je stejná rychlost. Bernoulliova rovnice v tvaru (4,91) tedy zřejmě neplatí, protože při rozdílných tlacích by na koncích vodorovné trubice musela být i rozdílná rychlost. V uvažované trubici však proudí viskózní tekutina, v které na rozdíl od ideální tekutiny k disipaci energie dochází.
Ve
výchozí rovnici
(4,94)
práce disipativních sil právě kompenzuje práci VDp
okolní tekutiny za podmínek, které uvažujeme při odvození Poiseuillova
zákona. V případě, že trubicí uvažovanou v rovnici
(4,94)
proudí
reálná tekutina, musíme do práce AI,II zahrnout i práci disipativních sil
působících v tekutině. Proudí-li tekutina laminárně, lze to učinit
explicitním započtením práce viskózních sil - alternativně tak lze odvodit
Poiseuillův zákon
(4,127)
. V případě turbulentního proudění trubicí, které
je pro hydrauliku podstatné, se práce disipativních sil zahrne do rovnice
(4,94)
jako celek vyjadřující ztrátovou energii. Velikost však již nelze určit na
základě jedné materiálové konstanty newtonovských tekutin (viskozity h),
případně známé tokové funkce
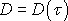 nenewtonovských tekutin, ale je nutné ji
stanovit experimentálně.
nenewtonovských tekutin, ale je nutné ji
stanovit experimentálně.
Pro hydraulické výpočty se takto upravená rovnice (4,94) přepíše do podoby (srov. [63])
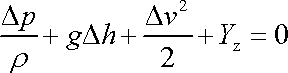 |
(4,210) |
nebo jako rovnice mezi výškami
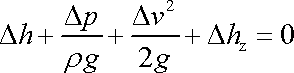 . . |
(4,211) |
Tyto rovnice jsou psány v tvaru analogickému Bernoulliově rovnici a je k nim přidán člen vystihující ztráty. V rovnici (4,210) je to veličina Yz nazývaná měrná ztrátová energie, v rovnici (4,211) veličina Dhz nazývaná ztrátová výška.
Protože
obě rovnice podobně jako Bernouliova rovnice vycházejí z rovnice
(4,94)
,
která říká, že práce vykonaná na systém se rovná přírůstku kinetické energie
soustavy, bývají často označovány také jako Bernoulliovy rovnice, přesněji Bernoulliovy rovnice pro proudění reálné
tekutiny. Závěry ze stati 4.3.4 však na tyto rovnice převést nelze a je
možné jen najít některé analogie. Tak např. rovnici
(4,210)
získáme z
rovnice
(4,88)
, převedeme-li všechny členy na levou stranu, potenciál V
vyjádříme dle
(4,90)
jako gh
a pro rozdíly veličin z levé a pravé strany rovnice
(4,88)
indexované 1, resp. 2, zavedeme označení
D.
Sčítance v rov.
(4,210)
mají rozměr
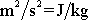 .
Měrná ztrátová energie tedy vyjadřuje ztracenou energii vztaženou na kilogram
proudící tekutiny. Sčítance v rovnici
(4,211)
, která vznikne
z rovnice
(4,210)
vydělením tíhovým zrychlením g , mají rozměr délky.
První sčítanec na levé straně rovnice se nazývá místní výška, druhý tlaková
výška a třetí rychlostní výška.
.
Měrná ztrátová energie tedy vyjadřuje ztracenou energii vztaženou na kilogram
proudící tekutiny. Sčítance v rovnici
(4,211)
, která vznikne
z rovnice
(4,210)
vydělením tíhovým zrychlením g , mají rozměr délky.
První sčítanec na levé straně rovnice se nazývá místní výška, druhý tlaková
výška a třetí rychlostní výška.
Aplikujeme-li rovnici (4,210) na případ ustáleného laminárního proudění viskózní newtonovské tekutiny vodorovnou trubicí všude stejného průřezu (viz obr.75), z kterého byl odvozen Poiseuillův zákon, dostaneme
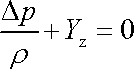 , , |
(4,212) |
protože jak Dh tak Dv2 jsou nulové. Z této rovnice plyne, dosadíme-li do ní za Dp z tvaru (4,135) Poiseuillovy rovnice, že velikost měrné ztrátové energie je pro tento případ dána rovnicí
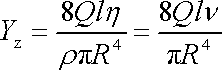 . . |
(4,213) |
Tedy
měrná ztrátová energie je přímo úměrná objemovému toku Q
, kinematické viskozitě
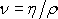 ,
délce potrubí l a nepřímo úměrná čtvrté
mocnině poloměru trubice R.
,
délce potrubí l a nepřímo úměrná čtvrté
mocnině poloměru trubice R.
V případě turbulentního proudění potrubím se nám již takový jednoznačný vzorec nepodaří sestavit. Tvar závislosti měrné ztrátové energie na objemovém toku se aproximuje vztahem
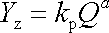 , , |
(4,214) |
kde exponent a roste od hodnoty a = 1 pro laminární proudění (viz rovnici (4,213) ) po hodnotu a = 2 pro plně turbulentní proudění, tj.pro Re>104. Výraz kp nazývaný někdy průtokovou konstantou vystihuje vlastnosti daného potrubí. Ty se vyjadřují empirickými vzorci zahrnujícími obvykle délku a průměr potrubí, součinitel délkových třecích ztrát l a součinitel místních ztrát z . Součinitel třecích ztrát l závisí na Reynoldsově čísle a hrubosti vnitřního povrchu potrubí. Součinitel místních ztrát z vystihuje odpor potrubí souvisící se zařazením různých armatur, kolen a zúžení či rozšíření potrubí. Hodnoty součinitelů bývají vystiženy empirickými vzorci a jsou pro jednotlivé typy a prvky potrubí udávány tabelárně či graficky. Často je musíme pro daný prvek určit experimentálně. Podrobněji se lze s užívanými postupy seznámit v knize [64] zaměřené na čerpací techniku, či v obecněji zaměřeném učebním textu [65].
Podobně
jako jsme v předchozí stati vycházeli z obecné věty, že práce
vykonaná na soustavu je rovna přírůstku kinetické energie soustavy (užili jsme
ji v úpravě
(4,94)
), vyjdeme v této stati z obecné věty o
hybnosti soustavy neboli první věty impulsové (I, stať 5.3.1), která říká, že
časová změna hybnosti soustavy
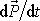 se rovná výsledné vnější síle
se rovná výsledné vnější síle
 působící na soustavu (I5,33);
působící na soustavu (I5,33);
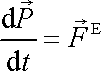 . . |
(4,215) |
Tuto
větu aplikujeme na jisté množství tekutiny (jistý počet částic tekutiny), jehož
objem V v průběhu času mění
svou polohu, tvar a v případě stlačitelné tekutiny i svou velikost. Tento
objem, který tekutina postupně zaujímá při svém pohybu, se nazývá tekutý objem. Aplikujeme-li na tekutý
objem rovnici
(4,215)
a jeho hybnost vyjádříme pomocí hustoty tekutiny r a její rychlosti
 ,
dostaneme
,
dostaneme
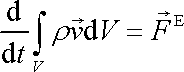 . . |
(4,216) |
Výsledná
vnější síla
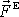 se skládá z výslednice objemových
sil
se skládá z výslednice objemových
sil
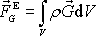 a výslednice plošných sil
a výslednice plošných sil
 ,
tj. sil, které na tekutý objem působí přes hraniční plochu S,
tedy
,
tj. sil, které na tekutý objem působí přes hraniční plochu S,
tedy
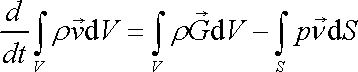 . . |
(4,217) |
 Rovnice
(4,217)
je vyjádřením první věty impulsové pro tekutý objem,
zanedbáme-li ve výrazu pro plošné síly smykovou složku obecného napětí a
předpokládáme, že okolí na vybraný tekutý objem může působit pouze tlakem p*).
V dalším se vzhledem k zaměření na hydrauliku omezíme jen na
jednoduché aplikace rov.
(4,217)
, obecnější pohled lze najít v [1],
čl.13.4 a 13.5.
Rovnice
(4,217)
je vyjádřením první věty impulsové pro tekutý objem,
zanedbáme-li ve výrazu pro plošné síly smykovou složku obecného napětí a
předpokládáme, že okolí na vybraný tekutý objem může působit pouze tlakem p*).
V dalším se vzhledem k zaměření na hydrauliku omezíme jen na
jednoduché aplikace rov.
(4,217)
, obecnější pohled lze najít v [1],
čl.13.4 a 13.5.
Jednoduchá,
ale prakticky velmi důležitá je aplikace rov.
(4,217)
na stacionární ustálené
proudění v zahnuté trubici, kterou si v hydraulice představujeme jako
reálnou trubici, tedy jako zahnutou část potrubí. Taková část potrubí (hovorově
koleno) je znázorněna na obr.92. Pro jednoduchost budeme předpokládat, že
trubice má všude stejný průřez a že
rozdíly v nadmořské výšce a ztráty rychlosti dané odporem trubice
lze v malém uvažovaném úseku zanedbat. Neuvažujeme v něm tedy
modifikace proudění vyšetřované v předchozí stati, všechny členy
v rov.
(4,210)
či
(4,211)
pokládáme za nulové. Potom je rychlost proudění
ve všech průřezech trubice stejná. Okamžitou časovou změnu hybnosti
 tekutiny obsažené v trubici mezi
průřezy S1 a S2 (viz obr.92), tj. výraz na levé straně
rovnice
(4,217)
, určíme jako rozdíl časových derivací hybnosti tekutiny
tekutiny obsažené v trubici mezi
průřezy S1 a S2 (viz obr.92), tj. výraz na levé straně
rovnice
(4,217)
, určíme jako rozdíl časových derivací hybnosti tekutiny
 ,
která průřezem S2 z trubice
vytéká, a hybnosti tekutiny
,
která průřezem S2 z trubice
vytéká, a hybnosti tekutiny
 ,
která průřezem S1 do trubice
vtéká;
,
která průřezem S1 do trubice
vtéká;
 . . |
(4,218) |
V rovnici
(4,218)
jsme po úvodních definičních úpravách na pravé straně třetí rovnice
užili z rovnice kontinuity
(4,52)
plynoucí závěr, že hmotnost
v trubici proudící tekutiny se nemění,
 ,
a na pravé straně čtvrté rovnice jsme hmotnost, která trubicí proteče za
jednotku času, tedy hmotnostní tok
(4,55)
, označili jeho standardním
znakem qm.
,
a na pravé straně čtvrté rovnice jsme hmotnost, která trubicí proteče za
jednotku času, tedy hmotnostní tok
(4,55)
, označili jeho standardním
znakem qm.
Změna
hybnosti tekutiny v trubici je způsobena silami na pravé straně rovnice
(4,217)
. Objemové síly v řešeném zjednodušeném případě neuvažujeme, a tedy
zbývá výsledná plošná síla
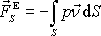 ,
která působením přes stěny trubice změní hybnost proudící tekutiny. Tato síla
je rovna změně hybnosti
(4,218)
. Reakcí na ní je síla
,
která působením přes stěny trubice změní hybnost proudící tekutiny. Tato síla
je rovna změně hybnosti
(4,218)
. Reakcí na ní je síla
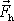 ,
kterou tekutina díky změně směru své hybnosti v zahnutém místě působí na
potrubí. Z předchozího pro ní plyne vyjádření
,
kterou tekutina díky změně směru své hybnosti v zahnutém místě působí na
potrubí. Z předchozího pro ní plyne vyjádření
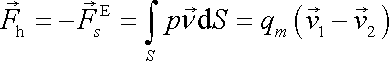 . . |
(4,219) |
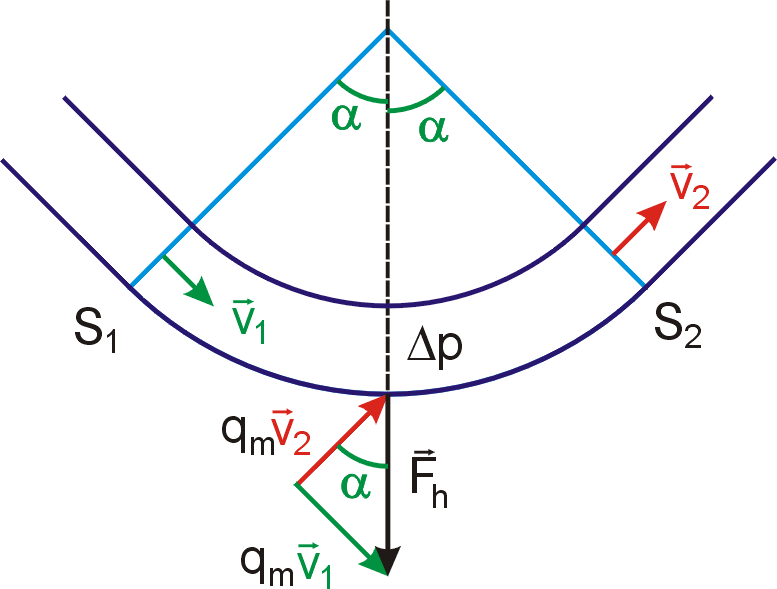
Na
obr.92 je znázorněn úhel ohybu potrubí
2a , síla
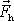 a vektorový trojúhelník zobrazující její
vznik. Z tohoto vektorového trojúhelníku plyne, že síla
a vektorový trojúhelník zobrazující její
vznik. Z tohoto vektorového trojúhelníku plyne, že síla
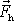 působí ve směru osy ohybu, míří ven
z ohybu a její velikost je dána výrazem
působí ve směru osy ohybu, míří ven
z ohybu a její velikost je dána výrazem
kde v značí velikost rychlosti tekutiny proudící potrubím, kterou pokládáme za konstantní v celém potrubí.
Proudí-li
potrubím reálná tekutina, musíme pro překonání odporu trubice, reprezentovaného
např. měrnou ztrátovou energií
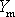 , na trubici působit přetlakem Dp. Z rov.
(4,210)
plyne, že pro udržení rovnoměrného proudění (Dv=0) v takové trubici, při předpokládaném zanedbání objemových
sil (člen gDh
z rovnice vypouštíme), musí platit
, na trubici působit přetlakem Dp. Z rov.
(4,210)
plyne, že pro udržení rovnoměrného proudění (Dv=0) v takové trubici, při předpokládaném zanedbání objemových
sil (člen gDh
z rovnice vypouštíme), musí platit
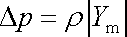 . . |
(4,221) |
Přetlak Dp podél trubice klesá. Zanedbáme-li velikost
poklesu mezi průřezy S1 a S2 , můžeme celé oblasti kolena z obr.92 přiřadit
jednu hodnotu přetlaku, v obrázku označenou Dp . Síly vyvolané přetlakem (zvýšením
tlaku oproti obvykle atmosférickému tlaku v okolí trubice) se
v rovných úsecích trubice vyrovnají, ale v místech ohybu, kde vnější
plocha trubice je větší než vnitřní plocha, dají nenulovou výslednici
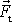 , která míří stejným směrem jako síla
, která míří stejným směrem jako síla
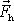 vyvolaná změnou hybnosti tekutiny.
vyvolaná změnou hybnosti tekutiny.
Sílu
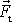 lze stanovit z následující úvahy. Kdyby
úsek trubice z obr.92 byl v místech průřezů S1 a S2 uzavřen a byl v něm
vyvolán tlak Dp, žádná výsledná síla by nevznikla, síla působící na vnější větší
plochu kolena by byla kompenzována silami působícími na plochy průřezů S1 a S2. Velikost součtu těchto sil, jejichž velikost je S Dp , a které míří ve směru vnějších
normál průřezů, je
lze stanovit z následující úvahy. Kdyby
úsek trubice z obr.92 byl v místech průřezů S1 a S2 uzavřen a byl v něm
vyvolán tlak Dp, žádná výsledná síla by nevznikla, síla působící na vnější větší
plochu kolena by byla kompenzována silami působícími na plochy průřezů S1 a S2. Velikost součtu těchto sil, jejichž velikost je S Dp , a které míří ve směru vnějších
normál průřezů, je
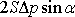 .
Součet sil míří dovnitř kolena ve směru jeho osy symetrie. Oba výsledky lze
snadno určit z obr.92. Součet sil kompenzuje sílu působící na vnější
plochu kolena. Na koleno tedy působí síla stejné velikosti opačně orientovaná.
Tato síla působí na koleno i v případě, kdy kapalina, v které je
přetlak Dp kolenem proudí.
V tom případě však již úsek trubice není v místech průřezů S1 a S2 uzavřen a síla není kompenzována. Pro velikost hledané síly
.
Součet sil míří dovnitř kolena ve směru jeho osy symetrie. Oba výsledky lze
snadno určit z obr.92. Součet sil kompenzuje sílu působící na vnější
plochu kolena. Na koleno tedy působí síla stejné velikosti opačně orientovaná.
Tato síla působí na koleno i v případě, kdy kapalina, v které je
přetlak Dp kolenem proudí.
V tom případě však již úsek trubice není v místech průřezů S1 a S2 uzavřen a síla není kompenzována. Pro velikost hledané síly
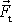 působící na koleno v důsledku přetlaku
tak dostáváme
působící na koleno v důsledku přetlaku
tak dostáváme
 , , |
(4,222) |
kde S je
označena plocha neproměnného průřezu trubice. Celková síla
 působící na úsek trubice zahnutý o úhel 2a (viz obr.92) protékaný reálnou tekutinou má
velikost
působící na úsek trubice zahnutý o úhel 2a (viz obr.92) protékaný reálnou tekutinou má
velikost
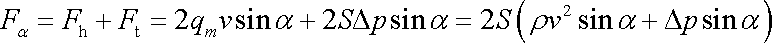 |
(4,223) |
a míří v ose zahnutí ven ze zahnuté části. Při závěrečné úpravě rovnice (4,223) jsme užili definičního vztahu hmotnostního toku qm (viz text u rov. (4,55) ). Hmotnost tekutiny, která projde průřezem S za jednotku času, jsme vyjádřili pomocí hustoty tekutiny r a její rychlosti v;
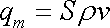 . . |
(4,224) |
Rovnice (4,223) a úvahy, kterými jsme k ní dospěli, nám nejen ukáží, jak musíme dimenzovat uchycení zahnutých částí potrubí, ale umožní nám i pochopit leckdy podivné chování hadic, kterými stříkáme zahradu či hasíme požár a jsou základem pro výklad činnosti vodních (mlýnských) kol a turbín.
Síly uvažované v rovnici (4,223) vznikají v důsledku změny směru vodního proudu, kterou v pevném potrubí jeho zahnutí způsobí. Pustíme-li do měkké hadice proud vody, snaží se síly typu (4,223) hadici narovnat. V rovné hadici tyto síly vymizí a proudění je stabilní. Chceme-li usměrnit stříkající proud, musíme sami vynaložit sílu, která hadici ohne, a tím změníme směr hybnosti tekutiny žádaným způsobem.
Konec hadice, z které tryská proud tekutiny, se chová jako tryska rakety (srov. I, čl.7.4); snaží se pohybovat v opačném směru, než z něj proudí tekutina. I tento jev lze vysvětlit nejen způsobem užitým v citovaném článku prvního dílu knihy, ale i způsobem užitým v této stati. Konec hadice je možno chápat jako otevřené ukončení systému, který na druhém konci je uzavřený. Můžeme si také představit, že hadici na konci ohneme a pak proti otevřenému konci stojí vnitřní stěna ohybu, na kterou působí místní tlak Dp , který v otevřeném konci hadice není kompenzován, a tlak vzniklý od změny směru hybnosti proudící tekutiny. Konec hadice je tedy proti směru z ní tryskající tekutiny unášen silou o velikosti
 , , |
(4,225) |
kde Dp je přetlak v místě konce trubice a k je součinitel závislý na stupni natočení hadice v blízkosti jejího konce. Pro rovný konec hadice je k = 0, otočíme-li konec hadice proti směru přicházejícího proudu tekutiny, tj. stočíme-li ji o úhel a=180o, je k = 2.
 Pro velké hasičské hadice stříkající silný
proud vody pod velkým přetlakem nabývá síla
(4,225)
značných hodnot. Proto je
manipulace s ní náročná vyžadující sílu jednoho, či více hasičů.
V současné době se ruční ovládání hasičské hadice nahrazuje umístěním
stříkaček na těžkých podvozcích či autech, kde je umístěna i cisterna
s vodou. Zajímavé efekty vyvolané silou
(4,225)
vznikají však i u tenkých
hadic, kterými zaléváme zahradu. Upustíme-li takovou hadici, její konec se hadovitě
pohybuje zpět a může kromě zahrady zalít i něco či někoho jiného.
Pro velké hasičské hadice stříkající silný
proud vody pod velkým přetlakem nabývá síla
(4,225)
značných hodnot. Proto je
manipulace s ní náročná vyžadující sílu jednoho, či více hasičů.
V současné době se ruční ovládání hasičské hadice nahrazuje umístěním
stříkaček na těžkých podvozcích či autech, kde je umístěna i cisterna
s vodou. Zajímavé efekty vyvolané silou
(4,225)
vznikají však i u tenkých
hadic, kterými zaléváme zahradu. Upustíme-li takovou hadici, její konec se hadovitě
pohybuje zpět a může kromě zahrady zalít i něco či někoho jiného.
Zařízení velmi názorně ukazující efekt síly (4,225) je znázorněno na obr. 93. Nazývá se Segnerovo kolo. Je to válcová nádoba, ke které jsou radiálně naletována ramena ukončená pravoúhle zahnutými tryskami do axiálního směru, jak je ukázáno na obrázku. Do nádoby uložené otočně na čepu nalijeme vodu a necháme ji tryskami vytékat. Síly působící na trysky roztočí kolo v naznačeném smyslu. Otáčení je zrychlené, přičemž zrychlení klesá s úbytkem vody ve válci až po vyrovnání s odporem čepu, které v závěru pohyb utlumí.
Další
důležitou oblastí hydrauliky, kde lze jevy výhodně vyložit prostřednictvím změn
hybnosti tekutiny
 ,
je zkoumání činnosti vodních kol a turbín. Nejprve v této souvislosti
vyšetříme, jakou silou působí dopadající proud tekutiny na nepohyblivou rovnou
stěnu kolmo postavenou ke směru proudu (viz obr.94). Hybnost tryskajícího
proudu tekutiny
,
je zkoumání činnosti vodních kol a turbín. Nejprve v této souvislosti
vyšetříme, jakou silou působí dopadající proud tekutiny na nepohyblivou rovnou
stěnu kolmo postavenou ke směru proudu (viz obr.94). Hybnost tryskajícího
proudu tekutiny
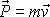 se o stěnu roztříští tak, že v ideálním
případě, který budeme dále uvažovat, částice kapaliny se budou podél stěny
pohybovat radiálně od místa dopadu proudu. Jejich množství i rychlost se
rozloží tak, že obraz proudění bude symetrický vůči bodu, kam dopadne střed
tryskajícího proudu. Celková hybnost tekutiny po dopadu na stěnu tak bude
nulová. Analogicky s rovnicí
(4,218)
pak pro změnu hybnosti tekutiny při
dopadu na stěnu dostáváme
se o stěnu roztříští tak, že v ideálním
případě, který budeme dále uvažovat, částice kapaliny se budou podél stěny
pohybovat radiálně od místa dopadu proudu. Jejich množství i rychlost se
rozloží tak, že obraz proudění bude symetrický vůči bodu, kam dopadne střed
tryskajícího proudu. Celková hybnost tekutiny po dopadu na stěnu tak bude
nulová. Analogicky s rovnicí
(4,218)
pak pro změnu hybnosti tekutiny při
dopadu na stěnu dostáváme

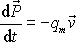 (4,226)
(4,226)
a pro sílu působící na stěnu, která je reakcí na sílu měnící hybnost tekutiny, pak dle (4,215) platí
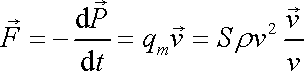 . . |
(4,227) |
V rovnicích
(4,226)
a
(4,227)
je
 rychlost tekutiny proudící přívodní trubicí
o průřezu S , qm hmotnostní tok touto trubicí a r hustota tekutiny.
rychlost tekutiny proudící přívodní trubicí
o průřezu S , qm hmotnostní tok touto trubicí a r hustota tekutiny.
Pro
činnost vodních kol a turbín je nejdůležitější zjistit, jaký maximální výkon
jim lze z proudící tekutiny předat. Výkon je dle I, rov. (I3,8) roven
součinu síly a rychlosti. Pro základní odhad vypočteme výkon, který tekutina
proudící rychlostí
 předá stěně kolmé k proudu, která se
pohybuje ve směru proudu rychlostí
předá stěně kolmé k proudu, která se
pohybuje ve směru proudu rychlostí
 .
Pro výkon dostaneme vyjádření
.
Pro výkon dostaneme vyjádření
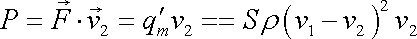 , , |
(4,228) |
v kterém
 je hmotnostní tok v místě ustupující
stěny, který je úměrný čtverci rozdílu rychlosti proudu a stěny. Zjistíme, pro
jakou rychlost stěny
je hmotnostní tok v místě ustupující
stěny, který je úměrný čtverci rozdílu rychlosti proudu a stěny. Zjistíme, pro
jakou rychlost stěny
 při dané rychlosti
při dané rychlosti
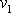 je tento výkon maximální. Položíme-li
derivaci výkonu podle rychlosti
je tento výkon maximální. Položíme-li
derivaci výkonu podle rychlosti
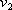 rovnu nule, dostaneme
rovnu nule, dostaneme
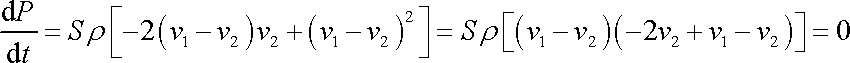 . . |
(4,229) |
Extrém
výkonu tedy nastane při
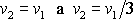 .
První hodnotě, kdy stěna proudu plně ustupuje, odpovídá minimum výkonu, protože
síla na stěnu a tedy i výkon jsou nulové. Druhý případ odpovídá hledanému
maximu, které v uvažovaném případě nastane, když stěna se pohybuje
třetinovou rychlostí, než je rychlost proudu tekutiny.
.
První hodnotě, kdy stěna proudu plně ustupuje, odpovídá minimum výkonu, protože
síla na stěnu a tedy i výkon jsou nulové. Druhý případ odpovídá hledanému
maximu, které v uvažovaném případě nastane, když stěna se pohybuje
třetinovou rychlostí, než je rychlost proudu tekutiny.
Uvedené příklady jenom hrubě naznačují, jak se při vyšetřování činnosti turbín a vodních kol postupuje. Podrobněji se problematikou zabývají Horákovy učebnice technické fyziky (např. [66]), detailní popis jednotlivých zařízení lze nalézt např. v [67]).
Výtok
tekutiny otvorem v nádobě závisí na rozdílu mezi tlakem v nádobě
 a tlakem v jejím okolí
a tlakem v jejím okolí
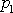 ,
na reologických vlastnostech tekutiny (viz kap.2) a na velikosti, tvaru a
povrchu otvoru. Při vyšších výtokových rychlostech je třeba respektovat
stlačitelnost plynů a jejich výtok studovat odděleně od výtoku kapalin.
Vytéká-li nestlačitelná tekutina hustoty
r z nádoby tak malým otvorem, že nemusíme
uvažovat pokles tlaku
,
na reologických vlastnostech tekutiny (viz kap.2) a na velikosti, tvaru a
povrchu otvoru. Při vyšších výtokových rychlostech je třeba respektovat
stlačitelnost plynů a jejich výtok studovat odděleně od výtoku kapalin.
Vytéká-li nestlačitelná tekutina hustoty
r z nádoby tak malým otvorem, že nemusíme
uvažovat pokles tlaku
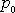 v nádobě v průběhu výtoku,
dostáváme z Bernoulliovy rovnice
(4,91)
pro rychlost výtoku
v nádobě v průběhu výtoku,
dostáváme z Bernoulliovy rovnice
(4,91)
pro rychlost výtoku
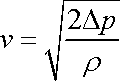 , , |
(4,230) |
kde
jsme označili Dp přetlak mezi nádobou a
okolím;
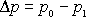 .
.
Nejběžnější aplikací rovnice
(4,230)
je případ, kdy kapalina
v tíhovém poli vytéká ze široké nádoby malým otvorem v hloubce
 .
Potom její rychlost je dána tzv. Torricelliůvým
vzorcem
.
Potom její rychlost je dána tzv. Torricelliůvým
vzorcem
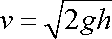 , , |
(4,231) |
neboť
přetlak Dp je v tomto případě
dán hydrostatickým tlakem, který dle
(4,20)
je roven rgh, kde g je velikost tíhového zrychlení. Zanedbání
poklesu tlaku
 v nádobě v průběhu výtoku zde
znamená, že při odvození rovnice
(4,231)
jsme zanedbali pokles volné hladiny
tekutiny v nádobě; v Bernoulliově rovnici
(4,91)
jsme položili
rychlost hladiny v nádobě
v nádobě v průběhu výtoku zde
znamená, že při odvození rovnice
(4,231)
jsme zanedbali pokles volné hladiny
tekutiny v nádobě; v Bernoulliově rovnici
(4,91)
jsme položili
rychlost hladiny v nádobě
 rovnu nule. Neučiníme-li toto zanedbání,
dostaneme pro rychlost výtoku kapaliny otvorem vzorec
rovnu nule. Neučiníme-li toto zanedbání,
dostaneme pro rychlost výtoku kapaliny otvorem vzorec
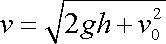 , , |
(4,232) |
který platí i pro výtok větším otvorem.
Rovnici
(4,230)
lze použít i pro plyn, vytéká-li z nádoby pod malým přetlakem Dp.. Vzorec
plyne z Bernoulliovy rovnice v tvaru
(4,91)
, tedy v tvaru
platném pro nestlačitelnou tekutinu. Lze jej tedy použít pouze, když je změna
hustoty plynu s poklesem tlaku zanedbatelná, např. pro vzduch za
normálních podmínek do výtokové rychlosti přibližně
 .
V těchto případech nemusíme mezi plynem a kapalinou rozlišovat a můžeme je
vyšetřovat společně jako tekutinu, jak jsme to dosud ve statích věnovaných
hydraulice dělali.
.
V těchto případech nemusíme mezi plynem a kapalinou rozlišovat a můžeme je
vyšetřovat společně jako tekutinu, jak jsme to dosud ve statích věnovaných
hydraulice dělali.
Objem
tekutiny vyteklé otvorem za jednotku času, tj. objemový tok
 (viz
(4,136)
), však nelze získat prostým
vynásobením plochy otvoru
(viz
(4,136)
), však nelze získat prostým
vynásobením plochy otvoru
 rychlostí výtoku
(4,230)
. Při výtoku
tekutiny dochází za výstupním otvorem ke zúžení (kontrakci) vytékajícího
paprsku a skutečný objemový tok
rychlostí výtoku
(4,230)
. Při výtoku
tekutiny dochází za výstupním otvorem ke zúžení (kontrakci) vytékajícího
paprsku a skutečný objemový tok
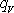 kapaliny otvorem vyjádříme jako
kapaliny otvorem vyjádříme jako
 ,
(4,233)
,
(4,233)
kde a je číslo menší než jedna. Číslo
 se nazývá činitel kontrakce (činitel zúžení) nebo též kontrakční číslo. Zúžení paprsku vytékající tekutiny je způsobeno
tím, že tekutina, která v nádobě je v klidu, nedosáhne výtokové
rychlosti dané rovnicemi
(4,230)
či
(4,231)
okamžitě v místě otvoru, ale
až v jisté vzdálenosti od otvoru. Na této vzdálenosti nekoná tekutina
rovnoměrný, ale zrychlený pohyb. Z rovnice kontinuity
(4,43)
plyne pro
průřez S1 v místě
zúžení paprsku
se nazývá činitel kontrakce (činitel zúžení) nebo též kontrakční číslo. Zúžení paprsku vytékající tekutiny je způsobeno
tím, že tekutina, která v nádobě je v klidu, nedosáhne výtokové
rychlosti dané rovnicemi
(4,230)
či
(4,231)
okamžitě v místě otvoru, ale
až v jisté vzdálenosti od otvoru. Na této vzdálenosti nekoná tekutina
rovnoměrný, ale zrychlený pohyb. Z rovnice kontinuity
(4,43)
plyne pro
průřez S1 v místě
zúžení paprsku
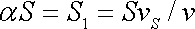 , , |
(4,234) |
kde
 je rychlost v místě otvoru plochy S
,
je rychlost v místě otvoru plochy S
,
 je plocha průřezu tekutiny v místě
kontrakce a v je výtoková rychlost daná rovnicí
(4,230)
, resp.
(4,231)
.
je plocha průřezu tekutiny v místě
kontrakce a v je výtoková rychlost daná rovnicí
(4,230)
, resp.
(4,231)
.
Činitel
kontrakce nabývá hodnot v intervalu
 .
Pro výtok kruhovým otvorem v tenké stěně nabývá činitel kontrakce hodnoty přibližně 0,6.
Vytvaruje-li se vhodně výstupní hubici, lze dosáhnout hodnot
.
Pro výtok kruhovým otvorem v tenké stěně nabývá činitel kontrakce hodnoty přibližně 0,6.
Vytvaruje-li se vhodně výstupní hubici, lze dosáhnout hodnot
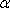 blízkých jedné. Někdy stačí
k podstatnému snížení kontrakce úprava výtokové hubice v tlustší
stěně. Tyto úpravy znamenají, že tvarem hubice usnadníme brzké dosažení konečné
výtokové rychlosti tekutiny v, kterou tekutina téměř dosáhne na
konci hubice. S problémem nalezení vhodného tvaru výtokové hubice se často
setkáváme v běžném životě, např. když chceme koupit dobrou čajovou konvici.
blízkých jedné. Někdy stačí
k podstatnému snížení kontrakce úprava výtokové hubice v tlustší
stěně. Tyto úpravy znamenají, že tvarem hubice usnadníme brzké dosažení konečné
výtokové rychlosti tekutiny v, kterou tekutina téměř dosáhne na
konci hubice. S problémem nalezení vhodného tvaru výtokové hubice se často
setkáváme v běžném životě, např. když chceme koupit dobrou čajovou konvici.
Uvažovanou
kontrakci paprsku jsme vysvětlili v rámci zákonů platných pro proudění ideální
tekutiny. Nezahrnuje tedy vliv viskozity či obecnějších reologických vlastností
proudící tekutiny a vliv tvarových či povrchových vlastností hubice na objemový
tok
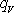 tekutiny vytékající z nádoby. Toto
snížení objemového toku se vystihuje rychlostním
činitelem j zavedeným analogicky jako činitel
kontrakce a (viz rov.
(4,233)
). Pro vodu se tento činitel
blíží jedné (
tekutiny vytékající z nádoby. Toto
snížení objemového toku se vystihuje rychlostním
činitelem j zavedeným analogicky jako činitel
kontrakce a (viz rov.
(4,233)
). Pro vodu se tento činitel
blíží jedné (
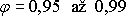 ) a lze ho tedy často zanedbat, ale pro
některé viskóznější látky, např. pro oleje, může být velmi podstatný. U
některých reologicky složitějších látek se může i stát, že zahrnutí jejich vlastností
rychlostním činitelem je nedostatečné a výtok těchto látek otvorem se musí
studovat jinými metodami, než jsou metody vyložené v této stati.
) a lze ho tedy často zanedbat, ale pro
některé viskóznější látky, např. pro oleje, může být velmi podstatný. U
některých reologicky složitějších látek se může i stát, že zahrnutí jejich vlastností
rychlostním činitelem je nedostatečné a výtok těchto látek otvorem se musí
studovat jinými metodami, než jsou metody vyložené v této stati.
Součin činitele kontrakce a rychlostního činitele se nazývá výtokový činitel a označuje se m..
Zahrneme-li i vlivy snížení výtoku tekutiny vystižené rychlostním činitelem j , dostaneme z rovnice (4,433) pro objemový tok otvorem
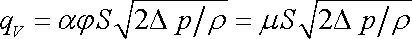 . . |
(4,235) |
Porovnáním objemového toku
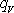 zjištěného z naměřeného objemu tekutiny,
která za určitý čas z nádoby vytekla, s jeho ideální hodnotou
zjištěného z naměřeného objemu tekutiny,
která za určitý čas z nádoby vytekla, s jeho ideální hodnotou
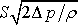 můžeme experimentálně zjistit hodnotu
výtokového činitele m.. Rozklad m na jeho
součinitele, tedy oddělení vlivu kontrakce a třecích ztrát na snížení výtoku z nádoby
už je obtížnější.
můžeme experimentálně zjistit hodnotu
výtokového činitele m.. Rozklad m na jeho
součinitele, tedy oddělení vlivu kontrakce a třecích ztrát na snížení výtoku z nádoby
už je obtížnější.
Výtok plynu při větším přetlaku
Výše v této stati jsme uvedli, že pro vzduch můžeme rov. (4,230) užít do rychlosti výtoku přibližně rovné 100 ms-1. Této poměrně vysoké výtokové rychlosti odpovídá přetlak
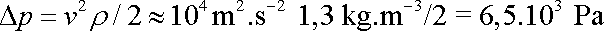 , , |
který
nedosahuje ani jedné desetiny atmosférického tlaku pat (
 ), tedy ani jedné desetiny atmosféry, kde
atmosférou rozumíme dříve často užívanou jednotku tlaku přibližně rovnou
atmosférickému tlaku (srov. stať 4.2.1).
), tedy ani jedné desetiny atmosféry, kde
atmosférou rozumíme dříve často užívanou jednotku tlaku přibližně rovnou
atmosférickému tlaku (srov. stať 4.2.1).
Pro
vyšší přetlak
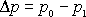 mezi tlakem
mezi tlakem
 v nádobě a tlakem
v nádobě a tlakem
 v prostoru , do kterého plyn vytéká
(expanduje), nelze již zanedbat změny hustoty plynu při tomto ději. Děj je
natolik rychlý, že nedojde k vyrovnání teploty mezi expandujícím plynem a
jeho okolím. Plyn se znatelně ochladí, někdy natolik, že dojde i k jeho
fázové změně. Např. když vypouštíme oxid uhličitý z tlakové nádoby, můžeme
jej dostat ve formě jehliček pevné látky, které se říká suchý led. I když
nebudeme přihlížet k těmto extrémním případům, nelze expanzi plynu
vyvolanou větším přetlakem pokládat za děj izotermický a musíme ji popisovat
jako děj adiabatický, při kterém se teplota plynu mění. Do mechaniky kontinua tak
přidáváme další veličinu - teplotu - a do řešení problému musíme zapojit
další disciplínu - termodynamiku (viz např. [51]).
v prostoru , do kterého plyn vytéká
(expanduje), nelze již zanedbat změny hustoty plynu při tomto ději. Děj je
natolik rychlý, že nedojde k vyrovnání teploty mezi expandujícím plynem a
jeho okolím. Plyn se znatelně ochladí, někdy natolik, že dojde i k jeho
fázové změně. Např. když vypouštíme oxid uhličitý z tlakové nádoby, můžeme
jej dostat ve formě jehliček pevné látky, které se říká suchý led. I když
nebudeme přihlížet k těmto extrémním případům, nelze expanzi plynu
vyvolanou větším přetlakem pokládat za děj izotermický a musíme ji popisovat
jako děj adiabatický, při kterém se teplota plynu mění. Do mechaniky kontinua tak
přidáváme další veličinu - teplotu - a do řešení problému musíme zapojit
další disciplínu - termodynamiku (viz např. [51]).
Uvažujeme-li stlačitelnost plynu, nemůžeme vyjít z Bernoulliovy rovnice v tvaru (4,91) , ale musíme použít obecnější tvar (4,84) , v kterém zanedbáme působení objemových sil, tedy vynecháme druhý člen rovnice. Na proudnici plynu porovnáme místo v nitru nádoby, kde položíme rychlost plynu rovnou nule a místo v oblasti otvoru, kde stanovíme výtokovou rychlost v. Z rovnice (4,84) pak plyne
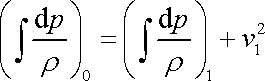 . . |
(4,236) |
Stanovíme nyní primitivní funkci
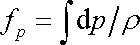 |
(4,237) |
k funkci
 pro případ adiabatického děje. Pro něj platí
rovnice.(viz např. [51])
pro případ adiabatického děje. Pro něj platí
rovnice.(viz např. [51])
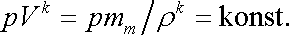 , , |
(4,238) |
kde V je objem jednoho molu plynu, mm jeho hmotnost. a
 je Poissonova konstanta, tj. poměr měrné
tepelné kapacity plynu při stálém tlaku, k měrné tepelné kapacitě při
stálém objemu. Z rovnice
(4,238)
plyne pro závislost hustoty plynu na jeho
tlaku vyjádření
je Poissonova konstanta, tj. poměr měrné
tepelné kapacity plynu při stálém tlaku, k měrné tepelné kapacitě při
stálém objemu. Z rovnice
(4,238)
plyne pro závislost hustoty plynu na jeho
tlaku vyjádření
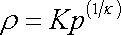 , , |
(4,239) |
kde K je konstanta. Dosadíme-li závislost (4,239) do (4,237) , dostaneme
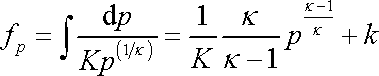 . . |
(4,240) |
Na
levou stranu Bernoulliovy rovnice
(4,236)
dosadíme hodnotu funkce fp pro bod uvnitř nádoby, tedy hodnotu
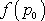 ,
a pro hodnotu primitivní funkce na pravé straně
,
a pro hodnotu primitivní funkce na pravé straně
 .
Hodnoty aditivní konstanty k
se objeví na obou stranách rovnice, a tedy vypadnou a z rovnice
(4,236)
po pracných, ale elementárních úpravách dostaneme pro výtokovou
rychlost plynu vyjádření
.
Hodnoty aditivní konstanty k
se objeví na obou stranách rovnice, a tedy vypadnou a z rovnice
(4,236)
po pracných, ale elementárních úpravách dostaneme pro výtokovou
rychlost plynu vyjádření
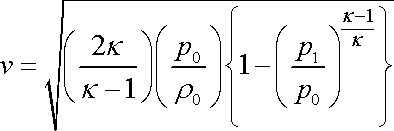 . . |
(4,241) |
Vzorec
(4,233)
však platí jen do kritické výtokové rychlosti, kterou je rychlost zvuku
v daném prostředí. Ta se ustaví, když poměr
 dosáhne jisté mezní hodnoty. Pro dvouatomový
plyn, jakým je v dobrém přiblížení i vzduch, je tato hodnota 0,53.
Poissonova konstanta pro takový plyn má hodnotu
dosáhne jisté mezní hodnoty. Pro dvouatomový
plyn, jakým je v dobrém přiblížení i vzduch, je tato hodnota 0,53.
Poissonova konstanta pro takový plyn má hodnotu
 .
K dosažení kritické výtokové rychlosti dvouatomového plynu tedy stačí, aby
tlak v nádobě, říkáme ji v této souvislosti též zásobník, byl
přibližně dvojnásobný oproti tlaku ve vnějším prostředí.
.
K dosažení kritické výtokové rychlosti dvouatomového plynu tedy stačí, aby
tlak v nádobě, říkáme ji v této souvislosti též zásobník, byl
přibližně dvojnásobný oproti tlaku ve vnějším prostředí.
Jak
jsme si již dříve v tomto článku říkali, při nadzvukových rychlostech je
třeba řešit problémy dynamiky tekutin zcela jiným způsobem (viz např.[59]),
než jejich modelováním ideální tekutinou, což jsme zde při odvození vztahu
(4,241)
učinili. Proto ani nepřekvapí, že pro hodnotu
 ,
tedy pro výtok do vakua, dá rovnice
(4,241)
zcela nerealistickou nulovou
hodnotu. Tuto rovnici musíme chápat jako rovnici, která dává přibližné
vyjádření výtokové rychlosti plynů, platné do té míry do jaké můžeme plyn
pokládat za ideální a výlučně pro rychlosti menší, než je rychlost zvuku v daném
prostředí při teplotě ve výtokové oblasti. Je-li tlak
,
tedy pro výtok do vakua, dá rovnice
(4,241)
zcela nerealistickou nulovou
hodnotu. Tuto rovnici musíme chápat jako rovnici, která dává přibližné
vyjádření výtokové rychlosti plynů, platné do té míry do jaké můžeme plyn
pokládat za ideální a výlučně pro rychlosti menší, než je rychlost zvuku v daném
prostředí při teplotě ve výtokové oblasti. Je-li tlak
 v prostoru, do kterého plyn vytéká
menší, než je tlak kritický
v prostoru, do kterého plyn vytéká
menší, než je tlak kritický
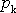 ,
zůstává již rychlost výtoku na své kritické hodnotě
,
zůstává již rychlost výtoku na své kritické hodnotě
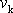 a dále se nezvyšuje. Pro tlaky
a dále se nezvyšuje. Pro tlaky
 velikost výtokové rychlosti na tlaku
velikost výtokové rychlosti na tlaku
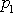 nezávisí. Jednoduchá rovnice pro výtokovou
rychlost
nezávisí. Jednoduchá rovnice pro výtokovou
rychlost
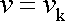 |
(4,242) |
tak
nahrazuje rovnici
(4,241)
pro tlaky
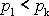 .
.
Při výtoku tenkým otvorem nastává i u plynů kontrakce proudu. Analogicky s rov. (4,235) můžeme pro objemový tok plynu psát rovnici
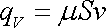 , , |
(4,243) |
kde m je výtokový činitel a výtoková rychlost v je nyní dána rovnicí (4,241) . Výtokový činitel u neupravených otvorů činí až 0,64. Pro jeho zvýšení, a tedy pro zlepšení výtoku plynu, se v praxi užívají výtokové hubice, u plynů se nazývají trysky nebo dýzy, vytvarované tak, aby co nejlépe vystihly zužování (kontrakci) volného paprsku. Vybavíme-li trysky leštěným povrchem a zaoblíme všechny hrany, lze dosáhnout hodnoty výtokového činitele m až 0,98.
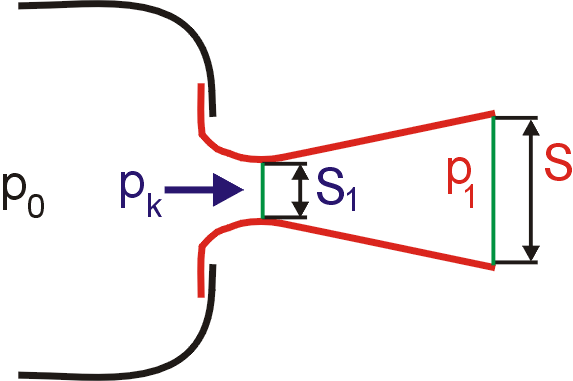 Existence kritické výtokové rychlosti plynů
nezávislé na zvyšování přetlaku
Existence kritické výtokové rychlosti plynů
nezávislé na zvyšování přetlaku
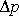 omezuje možnosti získání dostatečně velké
kinetické energie tryskajících plynů, což omezuje možnosti např. při konstrukci
raket nebo parních turbín. Existuje však způsob, jak vhodným uspořádáním
výtokové hubice zvýšit konečnou rychlost plynu opouštějícího systém nad hodnotu
kritické rychlosti
omezuje možnosti získání dostatečně velké
kinetické energie tryskajících plynů, což omezuje možnosti např. při konstrukci
raket nebo parních turbín. Existuje však způsob, jak vhodným uspořádáním
výtokové hubice zvýšit konečnou rychlost plynu opouštějícího systém nad hodnotu
kritické rychlosti
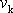 .
Děje se tak. užitím Lavalovy trysky znázorněné na obr.95.
Na rozdíl od běžných trysek má Lavalova tryska za nejužším místem rozšiřující
se část. Hodnota kritické rychlosti
.
Děje se tak. užitím Lavalovy trysky znázorněné na obr.95.
Na rozdíl od běžných trysek má Lavalova tryska za nejužším místem rozšiřující
se část. Hodnota kritické rychlosti
 nezávislé na přetlaku
nezávislé na přetlaku
 je dosažena v nejužším místě trysky
s průřezem Sk. Rozšíření trysky nemůže přinést zvýšení množství
(hmotnosti) plynu, který opouští nádobu, protože musí mezi průřezem Sk
a výstupním průřezem S být splněna rovnice kontinuity proudění.
Rozšíření trubice způsobí snížení tlaku pod jeho kritickou hodnotu
je dosažena v nejužším místě trysky
s průřezem Sk. Rozšíření trysky nemůže přinést zvýšení množství
(hmotnosti) plynu, který opouští nádobu, protože musí mezi průřezem Sk
a výstupním průřezem S být splněna rovnice kontinuity proudění.
Rozšíření trubice způsobí snížení tlaku pod jeho kritickou hodnotu
 ,
kterou nabývá v nejužším místě trysky. Okolní prostor o tlaku
,
kterou nabývá v nejužším místě trysky. Okolní prostor o tlaku
 je tak rozšiřující se částí trysky oddálen od
místa , kde je tlak kritický a hodnota jeho tlaku, tj.
je tak rozšiřující se částí trysky oddálen od
místa , kde je tlak kritický a hodnota jeho tlaku, tj.
 ,
je menší, než je hodnota kritického tlaku
,
je menší, než je hodnota kritického tlaku
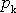 .
V celém systému od nádoby až po konec trysky tak dosáhneme většího
přetlaku
.
V celém systému od nádoby až po konec trysky tak dosáhneme většího
přetlaku
 ,
než je přetlak kritický a větší rychlosti výtoku plynu z trysky, než je
kritická rychlost
,
než je přetlak kritický a větší rychlosti výtoku plynu z trysky, než je
kritická rychlost
 .
Mluvíme o nadkritické rychlosti výtoku
dosažené zavedením Lavalovy trysky do systému.
.
Mluvíme o nadkritické rychlosti výtoku
dosažené zavedením Lavalovy trysky do systému.
Lavalova tryska může mít vrcholový úhel přibližně kuželovitého rozšíření nejvýše 10o, aby nedocházelo k odtržení proudu plynu od stěny a tím i ke vzniku nežádoucí kavitace, která silně narušuje materiál trysky. Podrobnější výklad o výtoku plynů lze najít. např. v [66] nebo [56].
Doposud jsme vždy předpokládali, že střední volná dráha molekul plynu je zanedbatelná vůči charakteristické délce (např. průměru) otvoru. U plynů za sníženého tlaku, tedy ve vakuové technice, je často třeba zkoumat případy výtoku plynu, kdy střední volná dráha molekul je srovnatelná s rozměry otvoru, případně i jiné otázky dynamiky plynů, kde rozměry zařízení a volná dráha molekul jsou srovnatelné. V takových případech nelze plyn pokládat za kontinuum a otázky jeho proudění je třeba řešit za přispění jiných teorii, zde konkrétně za přispění kinetické teorie plynů (viz např. [51]). Některé otázky na pomezí mechaniky a kinetické teorie plynů jsou řešeny též v [56].
*) V případě, že by byly zahrnuty i
smykové složky napětí
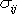 ,
výslednice plošných sil by byla dána výrazem
,
výslednice plošných sil by byla dána výrazem
 .
.