 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Při odvození Poiseuillova zákona jsme předpokládali, že
působením rozdílu tlaku
vznikne v trubici proudění, při kterém
jednotlivé válcové vrstvy kapaliny, jejichž osa je totožná s osou trubice,
se pohybují stálou rychlostí pouze ve směru osy válce. Podobně při proudění
znázorněném na obr.26, které uvažujeme při odvození Newtonova viskózního zákona
(2,47)
, předpokládáme, že jednotlivé vrstvy tekutiny kolmé ke směru změny
rychlosti mají stálou rychlost, jejíž směr leží v rovině vrstvy. Takové
proudění, při kterém nedochází k mísení tekutiny mezi jednotlivými
vrstvami, se nazývá laminární proudění.
Zvýšíme-li rozdíl tlaku
mezi konci trubice z obr.75 nad jistou
mez, kapalina z jednotlivých válcových vrstev se vlivem vyšších smykových
napětí působících mezi vrstvami začne promíchávat. Takovému proudění, při
kterém rychlost
v jednotlivých místech trubice kolísá
s časem, její složka do směru kolmého k ose trubice není vždy rovna
nule, při kterém dochází k porušení spojitého rozložení tekutiny
v trubici a vznikají víry, říkáme proudění
turbulentní. Pro popis rozdílu laminárního a turbulentního proudění není
podstatné, že jsme pro srovnání užili proudění v trubici. Podobně je možno
popsat turbulentní proudění i v jiných případech, než je proudění
v trubici, např. při proudění mezi dvěma různě rychle se pohybujícími
deskami, které v případě laminárního proudění bývá označováno jako
Couettovo proudění (srov. obr.3 nebo 26). V tomto případě by uvažované
vrstvy - laminy byly rovinné plochy.
Ve stacionárním laminárním proudění lze jednoduše oddělit proudnice a lze je i označit např. zbarvením částic kapaliny náležejících k jedné proudnici. V turbulentním proudění takový postup není možný, značkovací barvivo či plovoucí částečky se rychle promíchají do celého objemu turbulentně proudící tekutiny.
Zda v trubici nastane laminární nebo turbulentní
proudění, lze stanovit dle velikosti bezrozměrového výrazu
,
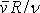kterému se říká Reynoldsovo číslo;
 . |
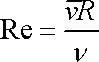(4,137) |
V rovnici
(4,137)
je symbolem Re označeno Reynoldsovo
číslo,
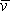je střední rychlost proudění v trubici,
R
poloměr trubice a
kinematická viskozita tekutiny definovaná
rovnicí
(4,119)
.
Je-li Reynoldsovo číslo
menší než jeho kritická hodnota
,
 , |
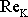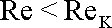(4,138) |
je proudění laminární. Pro
 |
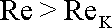(4,138) |
je proudění turbulentní.
Pro kritickou hodnotu Reynoldsova čísla pro proudění trubicí
bývají udávány různé velikosti v oboru
,
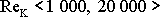nejčastěji však bývá uvažována hodnota 1000 až 2000. Máme-li např. trubici
poloměru
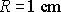protékanou vodou, jejíž teplota je 18 0C, je proudění laminární až
do kritické rychlosti proudění
,
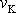která, uvažujeme-li
,
je rovna
 . |
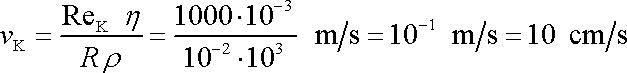V poslední rovnici jsme za viskozitu
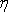vody, která při 18 0C je
,
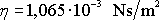dosadili přibližnou hodnotu
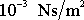a za hustotu vody přibližnou hodnotu
.
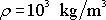Význam Reynoldsova čísla není omezen na proudění trubicí.
V Navierově - Stokesově rovnici
(4,116)
se vlastnosti tekutiny projeví
jedině její kinematickou viskozitou
(4,119)
.
Řešit rovnici
(4,116)
pro stacionární případ znamená najít pole rychlostí
 |
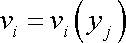(4,139) |
pro zvolený typ proudění. Ve výše vyšetřovaném případě bylo
zvoleno proudění trubicí poloměru R
průměrnou rychlostí
.
Sledujeme-li odpor, jakým působí prostředí na kouli poloměru R,
pohybuje-li se vůči němu rychlostí
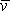(srov. Stokesův zákon
(4,145)
), jedná se o
jinou často uvažovanou volbu typu proudění. Proudí-li kapalina korytem daného
příčného průřezu, rychlost proudění
(4,139)
závisí opět na rychlosti
,
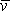na kinematické viskozitě n a na
zvoleném charakteristickém lineárním rozměru
l příčného průřezu koryta.
Rychlost
(4,139)
laminárního stacionárního proudění, které
lze popsat rovnicí
(4,116)
s okrajovými podmínkami zvolenými dle zadaného
typu proudění, závisí na třech parametrech: kinematické viskozitě n,
rychlosti
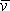a charakteristickém délkovém rozměru l.
Tyto veličiny mají fyzikální rozměr
 . |
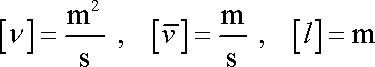(4,140) |
Lze z nich sestavit právě jednu nezávislou bezrozměrovou veličinu.
 , |
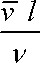kterou je právě Reynoldsovo číslo (4,137) . V posledním jeho vyjádření je pouze poloměr trubice R nahrazen obecným charakteristickým délkovým rozměrem l. Takto vyjádřené Reynoldsovo číslo
 |
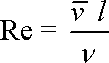(4,141) |
platí pro různá geometrická uspořádání. Hodnotu kritického Reynoldsova čísla je nutno pro jednotlivá geometrická uspořádání stanovit experimentálně.
Máme-li stacionární proudění jednoho geometrického typu,
která splňují podmínky platnosti Navierovy-Stokesovy rovnice
(4,116)
, jsou tato
proudění při stejném Reynoldsově čísle podobná. Stacionární řešení rovnice
(4,139)
,
resp.
,
lze totiž vždy zapsat v tvaru
 . |
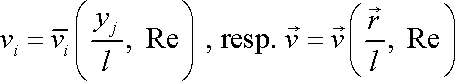(4,142) |
Při stejném Reynoldsově čísle závisí řešení rovnice pouze na
střední rychlosti
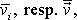a na poměru polohového vektoru
,
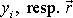k rozměru l, který je charakteristický pro daný typ proudění.
Bezrozměrové Reynoldsovo číslo vystihuje fyzikální podobnost různých proudění a bývá proto nazýváno podobnostním číslem.
Reynoldsovo číslo vystihuje fyzikální podobnost při stacionárním laminárním proudění popsaném Navierovou - Stokesovou rovnicí (4,116) . Další bezrozměrová podobnostní čísla (viz např. [1], čl. 18.3, [52], [53]) bývají užívána i pro jiné druhy proudění. Např. Machovo číslo
 , |
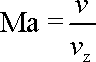(4,143) |
tj. poměr vzájemné rychlosti prostředí a obtékaného
předmětu v k rychlosti
zvuku
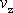se užívá při vyšetřování proudění, kde
rychlost v je blízká, či překračuje
rychlost zvuku. Pro nestacionární laminární proudění, kde k dříve
uvažovaným parametrům kinematické viskozitě
n, střední
rychlosti
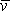a charakteristickému rozměru l,
přistupuje ještě perioda nestacionarity
t, se k Reynoldsovu
číslu připojuje ještě číslo Strouhalovo
 . |
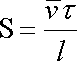(4,144) |
Podobnost proudění v tomto případě nastane při rovnosti obou podobnostních čísel, tj. Reynoldsova i Strouhalova.
Metody fyzikální podobnosti zjednodušují řešení úloh dynamiky tekutin. Jsou zvláště důležité pro přenášení výsledků hydrodynamických a aerodynamických zkoušek z modelů na skutečný objekt. Pro přenášení výsledků nestačí geometrická podobnost, ale je nutno dodržet fyzikální podobnost, která vyžaduje shodnost podobnostních čísel důležitých pro řešení daného problému.
|
|
|
|
|
|
|
|
|