---

---

4.4 Proudění viskózní tekutiny

Pro ideální tekutinu předpokládáme, že napětí v ní má pouze charakter tlaku

.

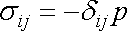(4,1)

V reálných tekutinách tento předpoklad není splněn. Pohybují-li se dvě sousední vrstvy reálné tekutiny různou rychlostí, vzniká mezi nimi smykové napětí. V prvním přiblížení předpokládáme, že velikost tohoto napětí je úměrná rozdílu rychlostí mezi vrstvami, jak je vyjádřeno Newtonovým viskózním zákonem (2,46) , respektive (2,48) . Celkové napětí v proudící newtonovské tekutině dostaneme, přidáme-li k tlakovému napětí (4,1) napětí 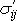vyvolané prouděním tekutiny;

.

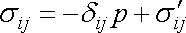(4,105)

V rovnici (4,105) je onačení 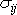užito pro celkové napětí a ne pro jeho část (4,1) , která značila celkové napětí pro ideální tekutinu.

Napětí 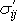můžeme dle (2,20) rozložit na symetrickou část a deviátor ;

.

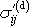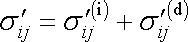(4,106)

Dle (2,46) deviátor napětí je pro newtonovskou látku úměrný deviátoru tenzoru rychlosti deformace ;

.

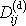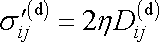(2,46)

O symetrické části tenzoru napětí budeme předpokládat, že je úměrná symetrické části 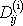tenzoru rychlosti deformace, tedy

.

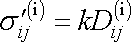(4,107)

Pro poloviční hodnotu konstanty k se užívá název druhá viskozita. Vyjadřuje viskózní odpor proti objemovým změnám. V kapalině se tedy její vliv na průběh proudění neuplatňuje. Též v plynu bývá většinou její vliv pro malou hodnotu této viskozity zanedbatelný. Je jí však třeba uvažovat při pohybu některých složitějších reologických látek.

Dle (2,16) je symetrická část 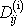tenzoru rychlosti deformace dána výrazem

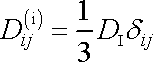(4,108)

a deviátor 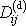tenzoru rychlosti deformace dle (2,17) výrazem

.

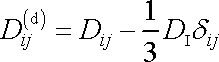(4,109)

Dosadíme-li do (4,105) z (4,106) , (2,46) a (4,107) , dostáváme pro napětí 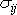v proudící viskózní tekutině vyjádření

,

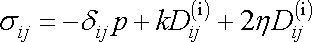(4,110)

které, užijeme-li rovnic (4,108) a (4,109) , můžeme dále přepsat na tvar

.

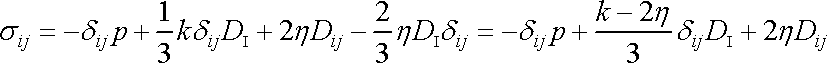(4,111)

Složky tenzoru rychlosti deformace jsou dle (1,62) dány výrazy

,

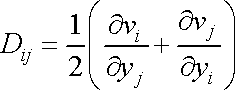(1,62)

a tedy první invariant tohoto tenzoru

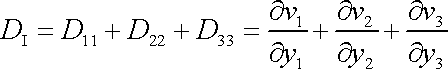je dle (4,59) roven divergenci vektoru rychlosti;

.

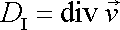(4,112)

Pro nestlačitelnou tekutinu, tj. kapalinu, je dle rovnice (4,65) 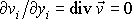, a tedy vyjádření tenzoru napětí (4,111) se zjednoduší na tvar

.

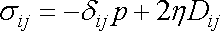(4,113)

Dosadíme-li vyjádření (4,113) tenzoru 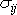do pohybové rovnice kontinua (3,13) , dostáváme po úpravách analogických těm, kterými jsme převedli rovnici (3,13) na tvar (4,67) , rovnici

.

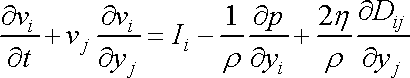(4,114)

Výraz 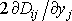lze upravit

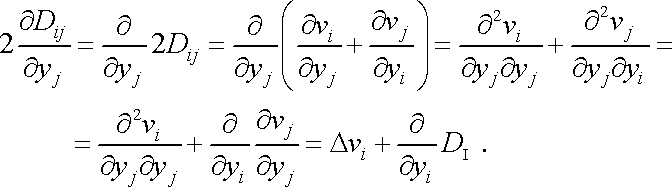(4,115)

Symbolem je označen Laplaceův operátor (viz [9], kap. 78). Vyjádření (4,115) dosadíme do rovnice (4,114) a znovu užijeme podmínku 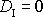platnou pro kapaliny, dostaneme

.

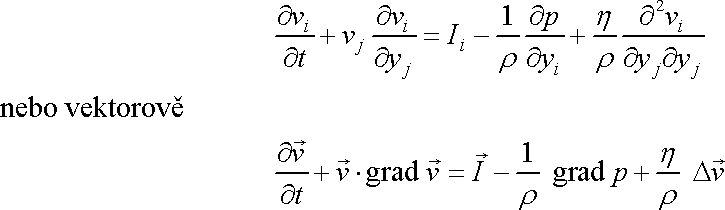(4,116)

Rovnice (4,116) je obvykle uvažovaným tvarem pohybové rovnice newtonovské viskózní kapaliny, pro niž se užívá názvu Navierova-Stokesova rovnice.

Pro stlačitelnou newtonovskou tekutinu musíme při dosazení do pohybové rovnice kontinua (3,13) užít vyjádření (4,111) pro napětí . Místo rovnice (4,114) pak dostaneme

.

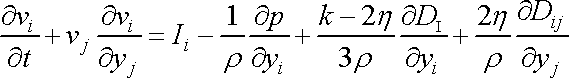(4,117)

Upravíme-li poslední člen na pravé straně rovnice (4,117) dle identity (4,115) , získáme po sloučení členů s výrazem 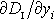rovnici

.

(4,118)

Je to Navierova-Stokesova rovnice pro stlačitelnou tekutinu.

Někdy nebývá uvažován viskózní mechanismus při objemových změnách. Neuvažuje se napětí úměrné rychlosti všestranné deformace, konstanta k v rovnici (4,107) a (4,118) se klade rovna nule. Rovnice (4,118) nabývá potom často uvažovaný tvar

.

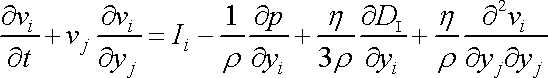(4,118´)

V rovnicích (4,116) , (4,118) a (4,118´) se vyskytuje poměr 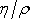viskozity k hustotě 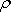. Tento poměr, který bývá často uvažován i při měření viskózních vlastností látek (viz [6], stať 2.5.5), se nazývá kinematická viskozita a označuje se symbolem ;

.

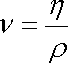(4,119)

Navierovy-Stokesovy rovnice spolu s rovnicí kontinuity (4,63) a s funkcí (4,6) 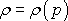tvoří úplný systém rovnic pro analytické řešení problému pohybu newtonovských viskózních tekutin. Řešení této soustavy při zadaných okrajových podmínkách je obtížné a nebudeme ho zde provádět. Některé příklady jsou řešeny v [1], kap. 18. V následující stati pouze vyšetříme, jak vypadá průtok viskózní kapaliny trubicí kruhového průřezu. Abychom nemuseli transformovat rovnici (4,116) do válcových souřadnic, vyšetříme tento problém na základě elementárních úvah.

4.4.1 Poiseuillův zákon

Mějme válcovou trubici, jíž proudí newtonovská viskózní kapalina. V trubici poloměru R uvažujeme souosou proudovou trubici poloměru r (obr.75). Místo z Navierových-Stokesových rovnic vyjdeme při řešení problému přímo z Newtonova viskózního zákona v tvaru (2,47) . Smysl zákona tkví v tom, že smykové napětí na ploše kolmé ke směru, v kterém se mění rychlost tekutiny, je úměrné změně rychlosti ve směru kolmém k uvažované ploše. Předpokládáme, že v trubici rychlost 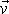má směr osy a její velikost v se mění pouze se vzdáleností od osy trubice, tj. v závislosti na poloměru r;

.

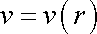(4,120)

Pro velikost smykového napětí na ploše kolmé k poloměru pak dle Newtonova viskózního zákona platí

.

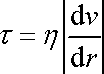(4,121)

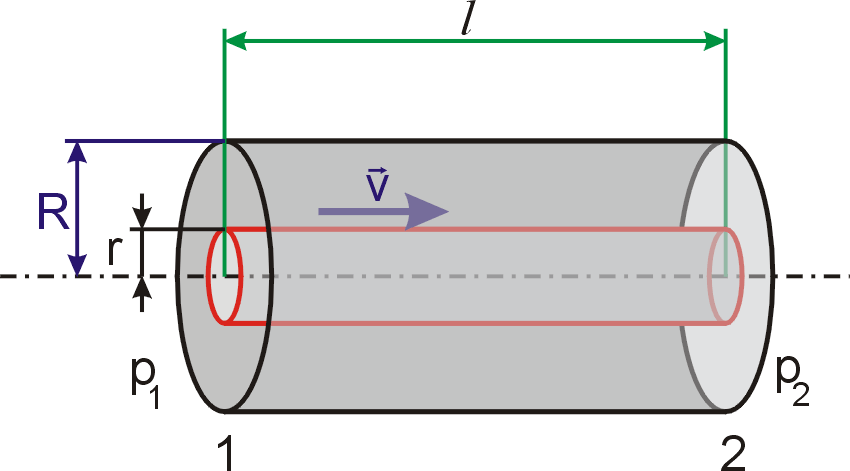
Má-li v trubici vzniknout ustálené proudění, a jen o takovém proudění budeme dále uvažovat, je nutné, aby výsledná síla působící na každou proudovou trubici byla nulová. Při nenulové výsledné síle by docházelo k zrychlenému pohybu, rychlost by se měnila s časem. Napíšeme podmínku nulové výsledné síly pro proudovou trubici naznačenou na obr.75. Zanedbáme-li objemové síly, podmínka zní

.

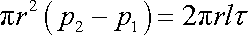(4,122)

Na levé straně rovnice (4,122) je rozdíl sil, které působí na podstavy proudové trubice; předpokládáme . Na pravé straně je výsledná smyková síla působící na plášť proudové trubice; délka trubice je l. Smyková síla působí proti smyslu pohybu, a proto její velikost na pravé straně rovnice (4,122) uvádíme s kladným znaménkem. Dle rovnic (4,120) a (4,121) je zřejmé, že na plášti uvažované proudové trubice má smykové napětí konstantní velikost a je kladné. Dosadíme-li do rovnice (4,122) za hodnotu (4,121) , dostaneme po úpravě

.

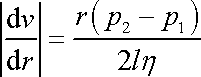(4,123)

Při malých rychlostech proudění předpokládáme, že viskózní tekutina má u pevné stěny stejnou rychlost jako stěna. V uvažovaném případě tedy rychlost na stěnách trubice je nulová;

.

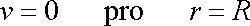(4,124)

Má-li dojít k pohybu, musí velikost rychlosti uvnitř trubice být kladná, a tedy 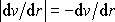. Potom z (4,123) plyne

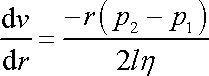a integrací dostáváme

.

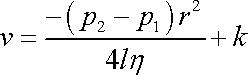Dosazením okrajové podmínky (4,124) do poslední rovnice určíme, že konstanta

,

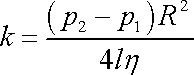a tedy

.

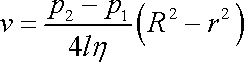(4,125)

Rovnice (4,125) představuje parabolický zákon rozdělení rychlosti. Na obr.76 je takové rozdělení rychlosti znázorněno v řezu trubicí.

Objem kapaliny Q, který proteče trubicí za jednotku času je dán integrálem

,

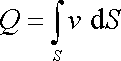(4,126)

v němž S značí průřez trubice. Dosadíme-li do integrálu (4,126) za v dle (4,125) a integraci provedeme v polárních souřadnicích , dostáváme postupně

.

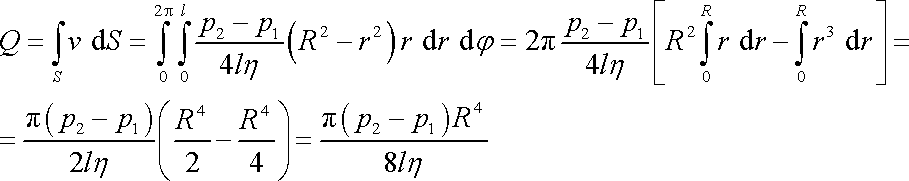Tedy objem V newtonovské viskózní kapaliny o viskozitě 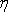proteklý za čas t trubicí poloměru R a délky l, mezi jejímiž konci je rozdíl tlaku 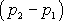, je dán výrazem

.

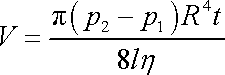(4,127)

Rovnice (4,127) je Poiseuillův zákon, který je výchozí rovnicí viskozimetrie newtonovských kapalin (viz [6], čl. 2.5.3).

Sledujeme-li proudění nenewtonovských kapalin, jejichž viskózní vlastnosti jsou charakteri-zované rovnicí toku (2,49)

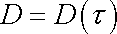(2,49)

válcovou trubicí poloměru R, vyjdeme z rovnice (4,126) , kterou postupně upravíme

.

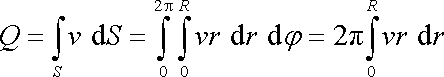(4,128)

Integrál integrujeme per partes

.

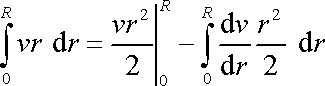(4,129)

První člen na pravé straně rovnice (4,129) je roven nule, neboť pro 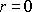je nulový výraz a pro , tj. u stěny trubice, je nulová velikost rychlosti kapaliny v .Rychlost deformace 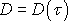je v uvažovaném případě rovna záporně vzatému výrazu ;

.

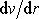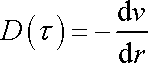(4,130)

Rovnice (4,122) platí i pro nenewtonovskou kapalinu. Vykrátíme-li ji výrazem , dostáváme po úpravě vztah

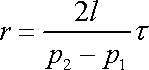(4,131)

mezi poloměrem r a smykovým napětím působícím na tomto poloměru. Dosadíme-li dle (4,129) , (4,130) a (4,131) do (4,128) , dostáváme

.

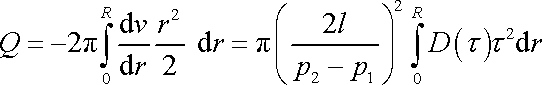Poslední integrál převedeme na integrál dle napětí . Podle (4,131) je 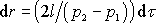, a tedy

.

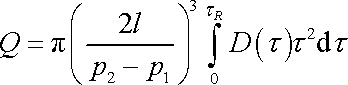(4,132)

Výraz 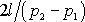můžeme vyjádřit jako poměr poloměru k napětí v libovolné vzdálenosti r od osy trubice, tedy též jako poměr poloměru R trubice k napětí 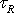u její stěny. Potom

.

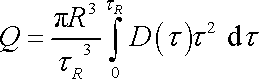(4,133)

Rovnice (4,133) je výchozí rovnice nenewtonovské kapilární viskozimetrie (viz [7], stať 10.3).

 

Pro newtonovskou látku je

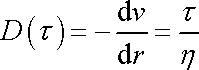(4,134)

a po dosazení této tokové funkce do (4,133) dostáváme

.

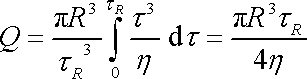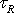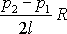Vyjádříme-li dle (4,131) jako , je

.

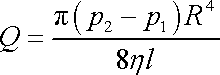(4,135)

Vynásobíme-li ještě rovnici (4,135) dobou průtoku t, dostáváme znovu Poiseuilleův zákon (4,127) .

 

V celé této stati jsme pracovali s veličinou Q značící objem kapaliny, který proteče trubicí za jednotku času. Tato veličina se nazývá objemový tok. Objemový tok tekutiny plochou S libovolně orientovanou ke směru rychlosti tekutiny se definuje rovnicí

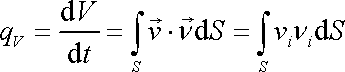(4,136)

analogicky jako hmotnostní tok rovnicí (4,55) . V rovnici (4,136) je V objem proteklé tekutiny, jednotkový vektor ve směru normály plochy a normou doporučené označení objemového toku.

 

---

---