Dynamiku kontinua jsme probrali v čl. 1.1. Tam vyložené metody Lagrangeova (1,1) a Eulerova (1,2) byly původně užívány právě pro popis proudění tekutin. Eulerův způsob udání rychlosti
 |
(4,44) |
částic tekutiny v daný okamžik t ve všech bodech
 ,
v kterých se tekutina nachází, je pro základní úvahy příhodnější, a proto
jej budeme dále užívat. Proudění budeme znázorňovat proudnicemi, tj. křivkami, jejichž tečny v každém bodě mají
směr vektoru rychlosti
,
v kterých se tekutina nachází, je pro základní úvahy příhodnější, a proto
jej budeme dále užívat. Proudění budeme znázorňovat proudnicemi, tj. křivkami, jejichž tečny v každém bodě mají
směr vektoru rychlosti
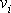 .
Tvar proudnic lze určit řešením rovnic
(1,5)
, dosadíme-li do nich vyjádření
rychlosti
.
Tvar proudnic lze určit řešením rovnic
(1,5)
, dosadíme-li do nich vyjádření
rychlosti
 dle
(4,44)
.
dle
(4,44)
.
*)
[*]
Poznámka: Vyjádříme-li v integrálu
(4,30)
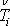 dle rovnice
(3,14)
jako
dle rovnice
(3,14)
jako
 a užijeme-li na úpravu integrálu
a užijeme-li na úpravu integrálu
 Gaussovu větu ([9], kap. 78, [1], čl. 1.8), dle níž
Gaussovu větu ([9], kap. 78, [1], čl. 1.8), dle níž
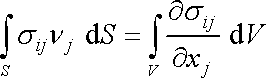 , , |
dostáváme z (4,31)
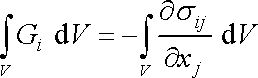 . . |
Odtud, vzhledem k tomu, že objem V je volen libovolně, plyne
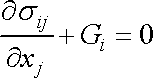 , , |
což je rovnice rovnováhy kontinua (3,8) .
[+] Volná hladina kapaliny je termín, který označuje plochu, kterou v běžné řeči označujeme jako hladinu kapaliny. Termín hladina se v teoriích pole užívá pro označení plochy, kde některá veličina nabývá konstantní hodnoty. Proto i v teorii hydrostatického pole se pojem hladina užívá v jiném významu než v běžné řeči.
[span>Při velmi malém naklonění by i na úzké straně vznikl moment síly navracející kvádr do plování na úzké straně, podobně jako můžeme minci při troše snahy postavit na její válcovou plochu. Pro plování na vodní hladině, kdy téměř vždy jsou přítomny síly porušující rovnováhu, není však případ velmi malého naklonění zajímavý a při posuzování otázek stability uvažujeme vždy o dostatečně velkých náklonech. Pro ně budou již dále prováděné úvahy včetně určení metacentra správné. Uvedený příklad ukazuje, že mechanika není pouze aplikovaná matematická analýza. Při zavádění metacentra nesmíme okolí bodu zvolit příliš malé, máme-li získat aplikovatelné výsledky úvah.
Jak jsme již uvedli v čl. 1.1, v obecném případě mají proudnice v různých okamžicích různý tvar. Pouze v případě stacionárního (ustáleného) proudění, kdy rychlosti jsou na čase nezávislé,
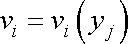 , , |
(4,45) |
je tvar proudnic po celou dobu pohybu tekutiny stejný a proudnice jsou shodné s trajektoriemi částic.
První Helmholtzova věta (1,17) udává, že obecně se pohyb tekutiny skládá z translačního, deformačního a otáčivého pohybu. Je-li v určité oblasti tekutiny výraz
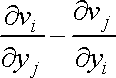 , , |
který v rovnici
(1,17)
odpovídá otáčivému (rotačnímu)
pohybu, různý od nuly, říkáme že proudění
tekutiny je vířivé. Vektorová
analýza (např. [9], kap. 78, [1], čl. 1.6) uvažuje ve vektorovém poli
 výraz o složkách
výraz o složkách
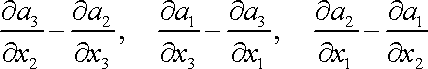 , , |
tj. dvojnásobnou hodnotu antisymetrické části tenzoru
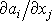 jako vektor.[*]
Nazývá jej rotací vektoru
jako vektor.[*]
Nazývá jej rotací vektoru
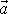 a označuje
a označuje
 .
Můžeme tedy říci, že při vířivém proudění je v určité oblasti tekutiny
rotace vektoru rychlosti
.
Můžeme tedy říci, že při vířivém proudění je v určité oblasti tekutiny
rotace vektoru rychlosti
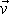 různá od nuly;
různá od nuly;
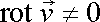 . . |
(4,46) |
Vektor
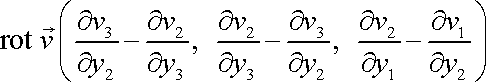 , , |
který je roven dvojnásobné hodnotě úhlové rychlosti
otáčení
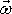 ,
(viz čl. 1.1, rovnici
(1,14)
), nazýváme vírem
rychlosti a označujeme jej
,
(viz čl. 1.1, rovnici
(1,14)
), nazýváme vírem
rychlosti a označujeme jej
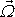 ;
;
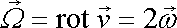 . . |
(4,47) |
Je-li v celé vyšetřované oblasti tekutiny vír rychlosti nulový,
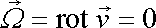 , , |
(4,48) |
říkáme, že proudění
je nevířivé. Ve vektorové analýze se
dokazuje, že vektor, který splňuje podmínku
(4,48)
, lze vyjádřit jako gradient
nějaké skalární funkce
 ,
tedy
,
tedy
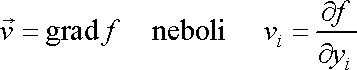 . . |
(4,49) |
Rovnice
(4,49)
je analogická rovnici (I3,21) (rozdíl ve
znaménku je nepodstatný). Funkci f
z rovnice
(4,49)
nazveme rychlostním potenciálem. Znalost
rychlostního potenciálu
 stačí k určení rychlosti nevířivého proudění
stačí k určení rychlosti nevířivého proudění
 .
Nevířivé proudění se proto též nazývá prouděním
potenciálovým.
.
Nevířivé proudění se proto též nazývá prouděním
potenciálovým.
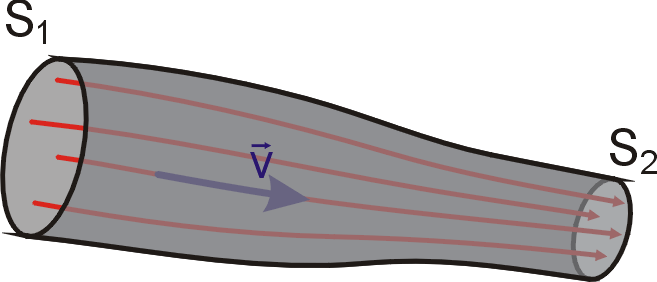 Při proudění musí být zachována hmotnost
tekutiny. Z tohoto jednoduchého předpokladu vycházíme při odvození rovnice
kontinuity proudění. Odvodíme ji nejprve ve tvaru vám známém ze středoškolského
studia [2], tj.
pro proudění tekutiny trubicí.
Při proudění musí být zachována hmotnost
tekutiny. Z tohoto jednoduchého předpokladu vycházíme při odvození rovnice
kontinuity proudění. Odvodíme ji nejprve ve tvaru vám známém ze středoškolského
studia [2], tj.
pro proudění tekutiny trubicí.
Mějme trubici znázorněnou na obr.68. Budeme předpokládat, že
proudění je stacionární. Na obr.68 je znázorněno několik proudnic a vektor rychlosti
 ,
který udává orientaci proudění uvažovanou v následujících slovních
formula-cích*). Průřezem
,
který udává orientaci proudění uvažovanou v následujících slovních
formula-cích*). Průřezem
 kolmým ke směru rychlosti vteče do trubice
za časový interval
kolmým ke směru rychlosti vteče do trubice
za časový interval
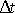 hmotnost tekutiny
hmotnost tekutiny
 .
(4,50)
.
(4,50)
Za stejně dlouhý časový interval vyteče průřezem
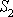 z trubice hmotnost tekutiny
z trubice hmotnost tekutiny
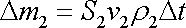 . . |
(4,51) |
Veličiny
 ,
,
 jsou průměrné hodnoty rychlosti a hustoty
v průřezu
jsou průměrné hodnoty rychlosti a hustoty
v průřezu
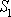 a
a
 ,
,
 průměrné hodnoty týchž veličin
v průřezu
průměrné hodnoty týchž veličin
v průřezu
 .
Předpokládáme stacionární proudění, a proto
.
Předpokládáme stacionární proudění, a proto
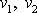 ,
,
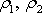 jsou konstantní hodnoty. Také hustota
v jednotlivých bodech uvnitř trubice se nemění s časem. Potom se
nemění ani hmotnost tekutiny obsažené v trubici; veškerá hmotnost, která
do trubice za časový interval
jsou konstantní hodnoty. Také hustota
v jednotlivých bodech uvnitř trubice se nemění s časem. Potom se
nemění ani hmotnost tekutiny obsažené v trubici; veškerá hmotnost, která
do trubice za časový interval
 vteče, z ní za stejný časový interval
musí vytéct. Tedy hmotnost
vteče, z ní za stejný časový interval
musí vytéct. Tedy hmotnost
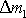 z rovnice
(4,50)
se musí rovnat
hmotnosti
z rovnice
(4,50)
se musí rovnat
hmotnosti
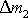 z rovnice
(4,51)
. Porovnáním obou
rovnic po vykrácení stejnou hodnotou
z rovnice
(4,51)
. Porovnáním obou
rovnic po vykrácení stejnou hodnotou
 dostáváme
dostáváme
Rovnice (4,52) je rovnice kontinuity pro stacionární proudění tekutiny v trubici.
Hustota kapaliny je konstantní,
 .
Rovnice
(4,52)
se pro kapalinu zjednoduší na tvar
.
Rovnice
(4,52)
se pro kapalinu zjednoduší na tvar
platný vzhledem k nestlačitelnosti kapaliny i pro nestacionární proudění.
Při odvozování rovnice
(4,52)
není podstatné, aby trubice z obr.68
měla pevné stěny. Důležité je jenom, aby tekutina se vyměňovala s okolím
pouze přes průřezy
 a ne pláštěm trubice. Tuto podmínku splňuje
nejen pevná reálná trubice, ale i myšlený útvar v tekutině, jehož plášť je
tvořen proudnicemi. Takový útvar se nazývá proudová
trubice [1] nebo též proudové vlákno [2]. Rovnice
(4,52)
a
(4,53)
platí
nejen v reálných trubicích, ale i v proudových trubicích.
a ne pláštěm trubice. Tuto podmínku splňuje
nejen pevná reálná trubice, ale i myšlený útvar v tekutině, jehož plášť je
tvořen proudnicemi. Takový útvar se nazývá proudová
trubice [1] nebo též proudové vlákno [2]. Rovnice
(4,52)
a
(4,53)
platí
nejen v reálných trubicích, ale i v proudových trubicích.
Uvedeme též obecnou formulaci rovnice kontinuity, tj. rovnici, která udává vztah mezi veličinami vztaženými k bodům proudového pole a ne vztah mezi průměrnými hodnotami v různých průřezech proudové trubice.
 Mysleme si uzavřenou plochu S pevnou v prostoru, kterou proudí
tekutina (obr.69). Hmotnost
Mysleme si uzavřenou plochu S pevnou v prostoru, kterou proudí
tekutina (obr.69). Hmotnost
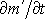 tekutiny, která za jednotku času vyteče přes
plochu S z objemu V omezeného touto plochou, je dána plošným
integrálem
tekutiny, která za jednotku času vyteče přes
plochu S z objemu V omezeného touto plochou, je dána plošným
integrálem
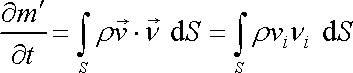 . . |
(4,54) |
V rovnici
(4,54)
je
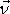 jednotkový vektor ve směru vnější normály
plochy. Výraz
jednotkový vektor ve směru vnější normály
plochy. Výraz
 je tok vektoru
je tok vektoru
 plochou
S (pojem tok vektoru viz např.[9], čl.
7.3 nebo [52], čl.
1.8). Vektor
plochou
S (pojem tok vektoru viz např.[9], čl.
7.3 nebo [52], čl.
1.8). Vektor
 udává hmotnost tekutiny prošlou průřezem
kolmým ke směru rychlosti
udává hmotnost tekutiny prošlou průřezem
kolmým ke směru rychlosti
 za jednotku času. Tok tohoto vektoru
plochou S, tedy výše uvedený výraz, se nazývá hmotnostní tok (např. [52], čl. 2.16);
za jednotku času. Tok tohoto vektoru
plochou S, tedy výše uvedený výraz, se nazývá hmotnostní tok (např. [52], čl. 2.16);
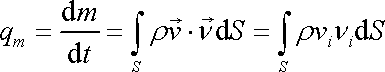 . . |
(4,55) |
 Na obr.70 je
znázorněn řez jednou z proudových trubic procházejících plochou S z obr.69. V předcházejícím odvození
rovnice kontinuity jsme tok hmotnosti za jednotku času plochou
Na obr.70 je
znázorněn řez jednou z proudových trubic procházejících plochou S z obr.69. V předcházejícím odvození
rovnice kontinuity jsme tok hmotnosti za jednotku času plochou
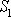 vyjádřili jako
vyjádřili jako
 ,
tok plochou
,
tok plochou
 jako
jako
 .
V integrálním vyjádření
(4,54)
pokládáme trubici za elementární. Tok
elementem plochy
.
V integrálním vyjádření
(4,54)
pokládáme trubici za elementární. Tok
elementem plochy
 ,
který obecně není kolmý k rychlosti
,
který obecně není kolmý k rychlosti
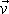 ,
vyjádříme jako
,
vyjádříme jako
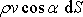 ,
kde
,
kde
 je úhel, který rovina elementu svírá
s rovinou příčného průřezu. V okolí místa 2, kde tekutina oblast
ohraničenou plochou S
opouští, je to úhel
je úhel, který rovina elementu svírá
s rovinou příčného průřezu. V okolí místa 2, kde tekutina oblast
ohraničenou plochou S
opouští, je to úhel
 ,
který svírá element průřezu
,
který svírá element průřezu
 s elementem průřezu
s elementem průřezu
 ,
průřezu kolmého k rychlosti
,
průřezu kolmého k rychlosti
 .
V okolí místa 1, kde tekutina vtéká do oblasti ohraničené plochou S,
je to úhel
.
V okolí místa 1, kde tekutina vtéká do oblasti ohraničené plochou S,
je to úhel
 mezi rovinou elementu
mezi rovinou elementu
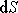 v tomto místě a rovinou elementu
průřezu
v tomto místě a rovinou elementu
průřezu
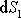 kolmého k rychlosti
kolmého k rychlosti
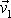 .
Násobení výrazem
.
Násobení výrazem
 zabezpečí přirozený požadavek, aby tok
plochami
zabezpečí přirozený požadavek, aby tok
plochami
 a jim příslušnými elementy
a jim příslušnými elementy
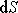 byl stejně velký.
byl stejně velký.
Úhel
 mezi rovinou elementu
mezi rovinou elementu
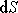 a rovinou průřezu kolmého
k rychlosti
a rovinou průřezu kolmého
k rychlosti
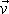 je stejný jako úhel mezi rychlostí
je stejný jako úhel mezi rychlostí
 a vnější normálou
a vnější normálou
 plochy
S v místě elementu
plochy
S v místě elementu
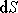 .
Proto lze
.
Proto lze
 nahradit skalárním součinem
nahradit skalárním součinem
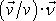 ,
který k absolutní hodnotě
,
který k absolutní hodnotě
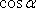 přidá ještě kladné znaménko v případě,
kdy tekutina z plochy S
vytéká (oblast 2) a záporné znaménko tam, kde tekutina proudí dovnitř
plochy S (oblast 1). Pro
elementární tok plochou
přidá ještě kladné znaménko v případě,
kdy tekutina z plochy S
vytéká (oblast 2) a záporné znaménko tam, kde tekutina proudí dovnitř
plochy S (oblast 1). Pro
elementární tok plochou
 tak dostáváme vyjádření
tak dostáváme vyjádření
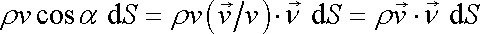 , , |
které stojí za integračním znakem v rovnici (4,54) .
Hmotnost m
obsaženou v objemu V
lze vyjádřit (viz I, čl. 5.1) jako
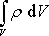 .
Změna
.
Změna
 hmotnosti za jednotku času
v objemu V je tedy dána výrazem
hmotnosti za jednotku času
v objemu V je tedy dána výrazem
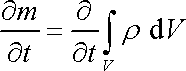 |
a je rovna záporně vzatému množství hmotnosti
 ,
které za jednotku času z objemu V
vyteče;
,
které za jednotku času z objemu V
vyteče;
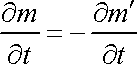 . . |
Porovnáním předposlední rovnice s rovnicí (4,54) pak dostáváme
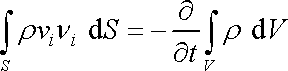 . . |
(4,56) |
Podle Gaussovy věty, citované v poznámce na str. 106,
je možné plošný integrál
 na levé straně rovnice
(4,56)
převést na
objemový integrál
na levé straně rovnice
(4,56)
převést na
objemový integrál
 .
Objem V je v prostoru stálý,
a proto lze vyměnit pořadí derivování a integrování na pravé straně rovnice
(4,56)
;
.
Objem V je v prostoru stálý,
a proto lze vyměnit pořadí derivování a integrování na pravé straně rovnice
(4,56)
;
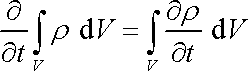 . . |
Rovnici (4,56) tedy můžeme přepsat na tvar
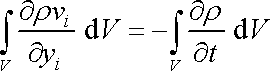 . . |
Převedeme-li oba integrály na jednu stranu rovnice a součet integrálů napíšeme jako integrál součtu, dostáváme
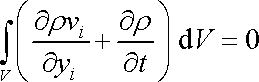 . . |
(4,57) |
Objem V byl v proudící tekutině zvolen libovolně. Rovnice (4,57) musí tedy být splněna pro každý objem V zvolený v tekutině. To však je možné jen tehdy, když integrand v integrálu (4,57) je roven nule v každém bodě tekutiny.
Rovnice (4,58) , která platí v každém bodě tekutiny, je obecnou formulací rovnice kontinuity proudění.
Ve vektorové analýze se skalární výraz
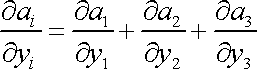 , , |
kde
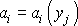 je vektorová funkce, nazývá divergence vektoru
je vektorová funkce, nazývá divergence vektoru
 a užívá se pro něj označení div
a užívá se pro něj označení div
 ;
;
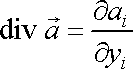 . . |
(4,59) |
S tímto označením lze rovnici (4,58) zapsat v tvaru
Výraz
 můžeme derivovat jako součin;
můžeme derivovat jako součin;
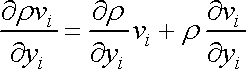 . . |
(4,61) |
Hustota
 je funkcí souřadnic a času
je funkcí souřadnic a času
 ,
tedy
,
tedy
 . . |
(4,62) |
V rovnici (4,58) upravíme první člen dle identity (4,61) , dostaneme
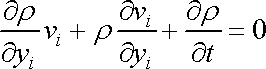 |
a za
 napíšeme
napíšeme
 ve shodě s
(4,62)
.
ve shodě s
(4,62)
.
Dostaneme další často užívaný tvar rovnice kontinuity
Zavedeme-li do rovnice divergenci
(4,59)
vektoru
rychlosti,
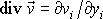 ,
můžeme rovnici
(4,63)
přepsat na tvar
,
můžeme rovnici
(4,63)
přepsat na tvar
Je-li tekutina nestlačitelná,
je
 a
a
 .
Pro kapalinu je rovnice kontinuity
vyjádřena jednoduchou podmínkou:
.
Pro kapalinu je rovnice kontinuity
vyjádřena jednoduchou podmínkou:
Pro obecnou analytickou formulaci problému proudění tekutin ([1], čl. 13.3) je třeba vedle rovnice kontinuity uvažovat i pohybovou rovnici tekutin. V čl. 3.1 jsme uvedli pohybovou rovnici kontinua (3,13)
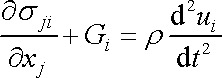 . . |
(3,13) |
Základním předpokladem o chování ideálních tekutin je
rovnice
(4,1)
, která udává, že napětí
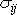 je dáno výrazem
je dáno výrazem
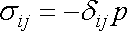 . . |
(4,1) |
Do rovnice
(3,13)
dosadíme za
 dle
(4,1)
a souřadnici označíme
dle
(4,1)
a souřadnici označíme
 .
Místo členu
.
Místo členu
 pak budeme psát
pak budeme psát
 .
Na pravé straně rovnice zrychlení
.
Na pravé straně rovnice zrychlení
 vyjádříme jako derivaci rychlosti dle
času
vyjádříme jako derivaci rychlosti dle
času
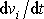 .
Dostaneme rovnici
.
Dostaneme rovnici
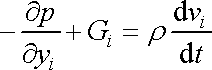 , , |
(4,66) |
jež je pohybovou rovnicí proudící ideální tekutiny. Upravíme
ji na obvykle uvažovaný tvar tím, že za výraz
 dosadíme dle identity
dosadíme dle identity
 |
a celou rovnici vydělíme hustotou
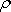 ,
dostaneme:
,
dostaneme:
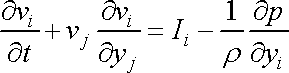 . . |
(4,67) |
Rovnice
(4,67)
, v které ve shodě s rovnicí
(4,8)
označujeme poměr
 jako intenzitu silového pole
jako intenzitu silového pole
 ,
se nazývá Eulerova hydrodynamická rovnice.
,
se nazývá Eulerova hydrodynamická rovnice.
Pro kapalinu (
 ) představují rovnice
(4,67)
a
(4,65)
systém
čtyř rovnic pro určení čtyř hledaných funkcí
) představují rovnice
(4,67)
a
(4,65)
systém
čtyř rovnic pro určení čtyř hledaných funkcí
 ,
,
 popisujících stav proudící kapaliny. Pro
stlačitelnou tekutinu je třeba k rovnicím
(4,67)
a
(4,63)
ještě připojit
známou závislost
(4,6)
popisujících stav proudící kapaliny. Pro
stlačitelnou tekutinu je třeba k rovnicím
(4,67)
a
(4,63)
ještě připojit
známou závislost
(4,6)
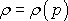 ,
aby bylo možno určit pět hledaných funkcí
,
aby bylo možno určit pět hledaných funkcí
 charakterizujících stav proudící stlačitelné
tekutiny. Přesné řešení hydrodynamických úloh dle uvedeného schématu je velmi
obtížné, neboť rovnice
(4,67)
není lineární rovnicí.
charakterizujících stav proudící stlačitelné
tekutiny. Přesné řešení hydrodynamických úloh dle uvedeného schématu je velmi
obtížné, neboť rovnice
(4,67)
není lineární rovnicí.
Dále budeme vyšetřovat pouze případy, kdy lze udat první integrál rovnice (4,67) , kterým je ze středoškolského studia známá Bernoulliova rovnice. V I, kap. 3 jsme získali první integrál pohybové rovnice hmotného bodu (I2,1)
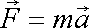 , , |
kterým je zákon zachování energie (I3,16)
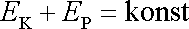 . . |
V uvedené kapitole jsme současně zaváděli pojmy práce a
energie, a proto postup od rovnice
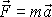 k rovnici
k rovnici
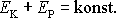 byl zdlouhavý. Nyní tento postup provedený
v I stručně zopakujeme.
byl zdlouhavý. Nyní tento postup provedený
v I stručně zopakujeme.
Pohybovou rovnici hmotného bodu
 ,
tj. 2. Newtonův zákon, promítneme do směru trajektorie hmotného bodu, a tento
průmět budeme integrovat podél trajektorie, získáme rovnici
,
tj. 2. Newtonův zákon, promítneme do směru trajektorie hmotného bodu, a tento
průmět budeme integrovat podél trajektorie, získáme rovnici
 . . |
(4,68) |
Poměr vektoru
 rychlosti hmotného bodu k velikosti
rychlosti v udává jednotkový tečný
vektor ve směru trajektorie, jehož smysl je shodný se smyslem pohybu hmotného
bodu. Konstanta k na pravé straně rovnice
(4,68)
odpovídá tomu, že primitivní funkce k dané funkci je určena až na
libovolnou volitelnou konstantu. Proto z rovnosti výrazů
rychlosti hmotného bodu k velikosti
rychlosti v udává jednotkový tečný
vektor ve směru trajektorie, jehož smysl je shodný se smyslem pohybu hmotného
bodu. Konstanta k na pravé straně rovnice
(4,68)
odpovídá tomu, že primitivní funkce k dané funkci je určena až na
libovolnou volitelnou konstantu. Proto z rovnosti výrazů
 neplyne přímo rovnost
neplyne přímo rovnost
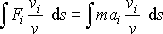 ,
ale rovnice
(4,68)
. Výraz na levé straně rovnice
(4,68)
značí práci sil
,
ale rovnice
(4,68)
. Výraz na levé straně rovnice
(4,68)
značí práci sil
 vykonanou na hmotný bod. Je-li pole sil
vykonanou na hmotný bod. Je-li pole sil
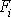 konzervativní, existuje k němu potenciální
energie
konzervativní, existuje k němu potenciální
energie
 a dle rov. (I3,21) platí
a dle rov. (I3,21) platí
 ,
tedy
,
tedy
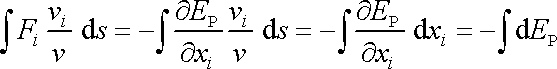 . . |
(4,69) |
Výraz
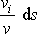 je speciální volbou libovolného
diferenciálního posunutí
je speciální volbou libovolného
diferenciálního posunutí
 v oboru souřadnic
v oboru souřadnic
 ,
v kterém je definováno silové pole
,
v kterém je definováno silové pole
 .
Proto můžeme v rovnici
(4,69)
položit
.
Proto můžeme v rovnici
(4,69)
položit
 .
.
Upravíme nyní pravou stranu rovnice (4,68) :
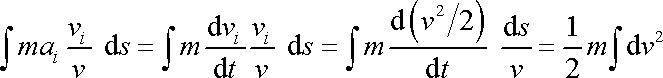 . . |
(4,70) |
V úpravě (4,70) užíváme identit
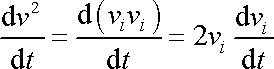 |
(4,71) |
a
 . . |
Dosadíme-li z (4,69) a (4,70) do (4,68) , dostáváme
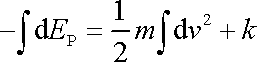 , , |
(4,72) |
a tedy
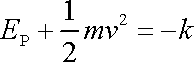 . . |
(4,73) |
Výraz
 je kinetická energie
je kinetická energie
 hmotného bodu a konstantu
hmotného bodu a konstantu
 můžeme označit konst. Dostáváme tedy hledané vyjádření (I3,16)
můžeme označit konst. Dostáváme tedy hledané vyjádření (I3,16)
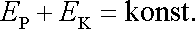 |
(4,74) |
zákona zachování mechanické energie hmotného bodu, který se
pohybuje v konzervativním silovém poli, tj. první integrál pohybové
rovnice
 .
.
Dle rovnice (4,74) součet potenciální energie v libovolném bodě trajektorie a kinetické energie hmotného bodu v okamžiku, kdy se v tomto bodě nachází, je pro všechny body trajektorie stejný. Tento výsledek lze získat též z rovnice (4,72) , nahradíme-li neurčité integrály určitými provedenými mezi libovolnými dvěma místy 1, 2 trajektorie (obr.71). Dostaneme tak rovnici
 , , |
(4,75) |
 neboť pro určité
integrály není třeba uvažovat konstantu
k. Z
(4,75)
plyne
neboť pro určité
integrály není třeba uvažovat konstantu
k. Z
(4,75)
plyne
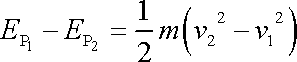 |
(4,76) |
neboli
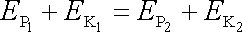 . . |
Ukázaný postup odvození prvního integrálu pohybové rovnice
hmotného bodu aplikujeme na odvození prvního integrálu Eulerovy hydrodynamické
pohybové rovnice
(4,67)
. Za integrační cestu zvolíme proudnici. Omezíme se při
tom na případ, kdy proudnice jsou s časem stálé, tedy na případ
stacionárního proudění. Při stacionárním proudění (viz
(4,45)
) není
rychlost
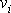 funkcí času
t, a tedy
funkcí času
t, a tedy
 ,
a rovnice
(4,67)
se zjednoduší na tvar
,
a rovnice
(4,67)
se zjednoduší na tvar
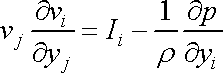 . . |
(4,77) |
Rovnici
(4,77)
vynásobíme jednotkovým vektorem
 ,
který má směr proudnice a smysl shodný s orientací rychlosti
,
který má směr proudnice a smysl shodný s orientací rychlosti
 částic. Vzniklý průmět do směru proudnice
budeme dle proudnice integrovat, dostaneme
částic. Vzniklý průmět do směru proudnice
budeme dle proudnice integrovat, dostaneme
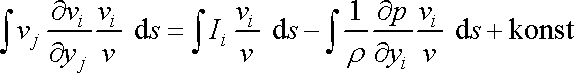 . . |
(4,78) |
Je-li pole objemových sil působících na tekutinu
konzervativní, můžeme dle (I3,25) složky intenzity pole vyjádřit jako záporně
vzaté parciální derivace potenciálu V
dle souřadnic (v proudící tekutině označujeme souřadnice
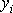 );
);
 . . |
(4,79) |
Stejně jako v předchozím odvození lze položit
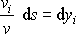 ,
a tedy
,
a tedy
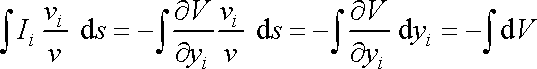 . . |
(4,80) |
Podobně
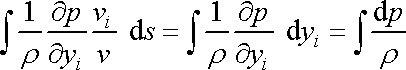 . . |
(4,81) |
Pro úpravu výrazu na levé straně rovnice (4,78) užijeme identitu
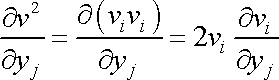 |
(4,82) |
analogickou s (4,71) ; dostaneme
 . . |
(4,83) |
Dosadíme-li z rovnic (4,80) , (4,81) a (4,83) do (4,78) , získáme, když převedeme všechny integrály na jednu stranu, rovnici
 |
neboli
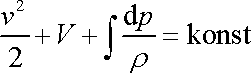 . . |
(4,84) |
Poslední rovnice je již hledaná Bernoulliova rovnice pro obecnou, tj. i stlačitelnou tekutinu.
Pro kapalinu je
 a integrál
a integrál
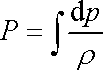 |
(4,85) |
v rovnici (4,84) můžeme snadno vypočítat;
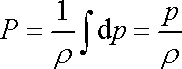 . . |
(4,86) |
Pro kapalinu má Bernoulliova rovnice jednoduchý tvar
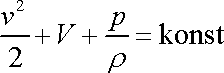 , , |
(4,87) |
který říká, že pro libovolná dvě místa 1, 2 na stejné proudnici (obr.72) se sobě rovnají výrazy

 .
(4,88)
.
(4,88)
Index označuje příslušnost veličiny k uvažovanému
místu, hustota je konstantní, tedy
 .
Vynásobíme-li rovnici
(4,87)
hustotou
.
Vynásobíme-li rovnici
(4,87)
hustotou
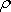 ,
dostáváme jiný, často užívaný tvar Bernoulliovy
rovnice:
,
dostáváme jiný, často užívaný tvar Bernoulliovy
rovnice:
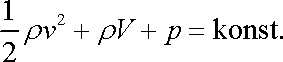 , , |
(4,89) |
který říká, že součet kinetické energie
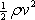 objemové jednotky kapaliny, její potenciální
energie
objemové jednotky kapaliny, její potenciální
energie
 a tlaku
p je podél proudnice konstantní.
a tlaku
p je podél proudnice konstantní.
Konstanty v rovnicích
(4,87)
a
(4,89)
neporovnáváme. Proto jsme užili pro obě stejného označení konst., i když druhá rovnice vznikne
z první násobením konstantní hustotou
 .
.
Potenciální energie hmotného bodu o hmotnosti m v tíhovém poli, když výšku počítanou od
libovolně zvolené hladiny nulového potenciálu označíme h,
je dána známým výrazem (I4,12)
 ,
a tedy potenciál
,
a tedy potenciál
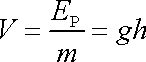 . . |
(4,90) |
Dosadíme-li vyjádření (4,90) za V do rovnice (4,89) , dostaneme Bernoulliovu rovnici pro kapalinu v tíhovém poli
Rovnice (4,87) , (4,88) , (4,89) a (4,91) lze užívat i pro plyny, nedochází-li k jejich velkému stlačení (kriteria lze nalézt v [1], kap. 14).
Chceme-li přesněji vystihnout chování plynů, musíme
vypočítat tlakovou funkci P
danou rovnicí
(4,85)
. Znamená to dosadit do
(4,85)
konkrétní tvar
závislosti
(4,6)
 .
Např. pro izotermický děj ideálního plynu je dle
(4,23)
.
Např. pro izotermický děj ideálního plynu je dle
(4,23)
 ,
a tedy
,
a tedy
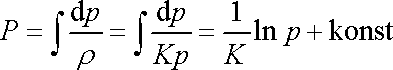 . . |
(4,92) |
Dosadíme-li dle (4,92) do rovnice (4,82) a užijeme-li společného označení pro aditivní konstanty obou rovnic, dostáváme Bernoulliovu rovnici
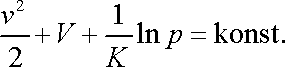 |
(4,93) |
pro izotermické proudění ideálního plynu.
Rovnici
(4,84)
lze odvodit ([1], čl. 14.1) pro nevířivé
stacionární proudění jako rovnici platnou v celém prostoru, v kterém
kapalina proudí. Konstanta na pravé straně rovnice je stejná pro všechny body,
jimiž tekutina proudí a nejen pro body jedné proudnice. Je však nutno
upozornit, že podmínka
(4,48)
 nevířivého proudění je přísná a řada
technicky důležitých druhů proudění ji nesplňuje. Např. často uvažované
Couettovo proudění
(1,65)
má z parciálních derivací
nevířivého proudění je přísná a řada
technicky důležitých druhů proudění ji nesplňuje. Např. často uvažované
Couettovo proudění
(1,65)
má z parciálních derivací
 nenulovou pouze derivaci
nenulovou pouze derivaci
 ,
a tedy nenulovou třetí složku
,
a tedy nenulovou třetí složku
víru rychlosti
 .
Proto je v aplikacích často výhodnější vycházet z předcházejícího
odvození a rovnici
(4,84)
pokládat za splněnou pouze podél jednotlivých
proudnic.
.
Proto je v aplikacích často výhodnější vycházet z předcházejícího
odvození a rovnici
(4,84)
pokládat za splněnou pouze podél jednotlivých
proudnic.
 K rovnici
(4,91)
lze dojít i elementární
úvahou, sledujeme-li stacionární proudění kapaliny v tíhovém poli
v jedné prou-dové trubici. Na obr.73 je naznačen průřez takovou trubicí.
Na začátku sledova-ného časového intervalu
K rovnici
(4,91)
lze dojít i elementární
úvahou, sledujeme-li stacionární proudění kapaliny v tíhovém poli
v jedné prou-dové trubici. Na obr.73 je naznačen průřez takovou trubicí.
Na začátku sledova-ného časového intervalu
 se nachází uvažované množ-ství kapaliny
v poloze I mezi plně vytaženými průřezy
se nachází uvažované množ-ství kapaliny
v poloze I mezi plně vytaženými průřezy
 a
a
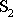 .
Na konci intervalu přejde do polohy II mezi čárkovaně značené průřezy. Dle věty
(I5,65) práce vykonaná všemi silami působícími na soustavu je rovna přírůstku
kinetické energie soustavy. Rozdíl kinetické energie
.
Na konci intervalu přejde do polohy II mezi čárkovaně značené průřezy. Dle věty
(I5,65) práce vykonaná všemi silami působícími na soustavu je rovna přírůstku
kinetické energie soustavy. Rozdíl kinetické energie
 uvažovaného množství kapaliny, přejde-li
z polohy I do polohy II, je tedy roven práci
uvažovaného množství kapaliny, přejde-li
z polohy I do polohy II, je tedy roven práci
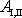 vykonané všemi silami na uvažované množství
kapaliny při provedeném posunu, tedy
vykonané všemi silami na uvažované množství
kapaliny při provedeném posunu, tedy
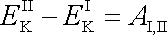 . . |
(4,94) |
Rozdíl kinetických energií
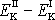 v poloze I a II je dán rozdílem
kinetických energií částí vyšrafovaných na obr.68. Kinetická energie společné
části poloh I, II (na obr.68 je tato část nešrafovaná) je při uvažovaném
stacionárním proudění stejná pro obě polohy kapaliny. Můžeme tedy psát
v poloze I a II je dán rozdílem
kinetických energií částí vyšrafovaných na obr.68. Kinetická energie společné
části poloh I, II (na obr.68 je tato část nešrafovaná) je při uvažovaném
stacionárním proudění stejná pro obě polohy kapaliny. Můžeme tedy psát
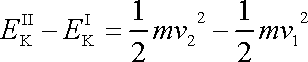 , , |
(4,95) |
kde
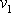 je průměrná velikost rychlosti kapaliny ve
vyšrafované oblasti u průřezu
je průměrná velikost rychlosti kapaliny ve
vyšrafované oblasti u průřezu
 a
a
 průměrná velikost rychlosti ve druhé
vyšrafované oblasti. Objem
průměrná velikost rychlosti ve druhé
vyšrafované oblasti. Objem
 první vyšrafované oblasti je v uvažovaném
přiblížení dán vztahem
první vyšrafované oblasti je v uvažovaném
přiblížení dán vztahem
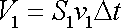 |
(4,96) |
a objem
 druhé oblasti je
druhé oblasti je
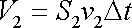 . . |
(4,97) |
Dle rovnice kontinuity, kterou zde můžeme užít v tvaru (4,53) je
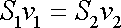 , , |
(4,53) |
a tedy
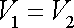 . . |
(4,98) |
Jelikož
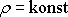 ,
je hmotnost
,
je hmotnost
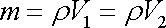 |
(4,99) |
obou vyšrafovaných oblastí stejná. Tento výsledek jsme již intuitivně užili v rovnici (4,95) .
Práce
 uvažovaná v rov.
(4,94)
se skládá
z práce tíhové síly a z práce, kterou na uvažované množství kapaliny
vykoná ostatní kapalina. První část práce
uvažovaná v rov.
(4,94)
se skládá
z práce tíhové síly a z práce, kterou na uvažované množství kapaliny
vykoná ostatní kapalina. První část práce
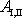 vyjádříme jako záporně vzatý rozdíl
vyjádříme jako záporně vzatý rozdíl
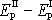 potenciálních energií kapaliny v poloze I a II, pro který
v analogii s rovnicí
(4,49)
napíšeme vyjádření
potenciálních energií kapaliny v poloze I a II, pro který
v analogii s rovnicí
(4,49)
napíšeme vyjádření
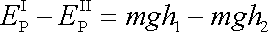 . . |
(4,100) |
V rovnici
(4,100)
je
 průměrná výška první vyšrafované oblasti
a
průměrná výška první vyšrafované oblasti
a
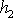 průměrná výška druhé vyšrafované oblasti nad
zvolenou nulovou hladinou potenciální energie. Druhá část práce
průměrná výška druhé vyšrafované oblasti nad
zvolenou nulovou hladinou potenciální energie. Druhá část práce
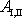 je dána rozdílem kladné práce, kterou vykoná
průměrná síla
je dána rozdílem kladné práce, kterou vykoná
průměrná síla
 působící na průřez
působící na průřez
 ,
posune-li se kapalina z polohy I do polohy II a záporné práce, která se
spotřebuje na posunutí kapaliny proti síle
,
posune-li se kapalina z polohy I do polohy II a záporné práce, která se
spotřebuje na posunutí kapaliny proti síle
 u průřezu
u průřezu
 .
Velikost posunu u průřezu
.
Velikost posunu u průřezu
 je
je
 ,
posun u průřezu
,
posun u průřezu
 je
je
 .
Vyjádříme-li velikost síly
.
Vyjádříme-li velikost síly
 jako
jako
 ,
kde
,
kde
 je
průměrná hodnota tlaku v první vyšrafované oblasti, a velikost síly
je
průměrná hodnota tlaku v první vyšrafované oblasti, a velikost síly
 jako
jako
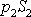 ,
kde
,
kde
 je průměrná hodnota tlaku ve druhé
vyšrafované oblasti, můžeme pro druhou část práce
je průměrná hodnota tlaku ve druhé
vyšrafované oblasti, můžeme pro druhou část práce
 napsat vyjádření
napsat vyjádření
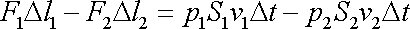 . . |
Celá práce
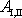 je pak dána výrazem
je pak dána výrazem
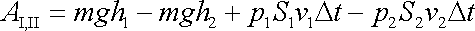 . . |
V posledních dvou členech rovnice lze dle
(4,96)
,
(4,97)
a
(4,99)
za
 a
a
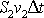 položit
položit
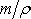 .
Práci
.
Práci
 pak můžeme napsat jako
pak můžeme napsat jako
 . . |
(4,101) |
Do rovnice
(4,94)
dosadíme vyjádření práce
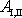 dle
(4,101)
a rozdílu
dle
(4,101)
a rozdílu
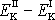 kinetických energií dle
(4,95)
; dostaneme:
kinetických energií dle
(4,95)
; dostaneme:
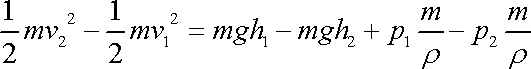 . . |
Po vykrácení hmotností
m, vynásobení hustotou
 a rozdělení členů dle indexů na jednotlivé
strany získá poslední rovnice tvar
a rozdělení členů dle indexů na jednotlivé
strany získá poslední rovnice tvar
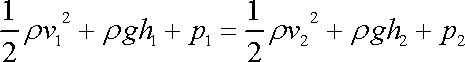 . . |
(4,102) |
Rovnice
(4,102)
udává vztah mezi průměrnými hodnotami
rychlostí, výšek a tlaků ve dvou různých libovolně volených oblastech (na
obr.68 značených šrafovaně) jedné proudové trubice. Provedeme-li limitní
přechod, při kterém zmenšujeme k nule rozměry oblastí, přejde proudová
trubice v proudnici a průměrné hodnoty v oblasti se stanou hodnotami
vztaženými k jednomu bodu na proudnici. Žádný z členů v rovnici
(4,102)
nezávisí přímo na rozměrech uvažovaných oblastí, a proto se tvar
rovnice
(4,102)
limitním přechodem nemění. Pokládáme-li rovnici
(4,102)
za
platnou podél proudnice, je její obsah shodný s obsahem rovnice
(4,91)
,
neboť rovnost výrazů
 ve dvou libovolných bodech proudnice je
totožný výsledek s tvrzením, že výraz je podél proudnice konstantní;
ve dvou libovolných bodech proudnice je
totožný výsledek s tvrzením, že výraz je podél proudnice konstantní;
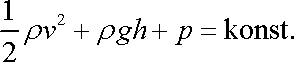 . . |
(4,91) |
 Základním důsledkem Bernoulliovy rovnice
(4,91)
je zmenšení tlaku v zúženém místě trubice protékané kapalinou
(obr.74). Tento zdánlivě paradoxní výsledek - bývá označován jako hydrodynamický paradox - je jednoduchým důsledkem rovnice
(4,91)
.
Mysleme si proudnici znázorněnou na obr.74 a na ní dvě místa označená 1 a 2.
Dle
(4,91)
nebo
(4,102)
dostaneme
Základním důsledkem Bernoulliovy rovnice
(4,91)
je zmenšení tlaku v zúženém místě trubice protékané kapalinou
(obr.74). Tento zdánlivě paradoxní výsledek - bývá označován jako hydrodynamický paradox - je jednoduchým důsledkem rovnice
(4,91)
.
Mysleme si proudnici znázorněnou na obr.74 a na ní dvě místa označená 1 a 2.
Dle
(4,91)
nebo
(4,102)
dostaneme
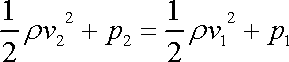 . . |
(4,103) |
Předpokládáme, že trubice je vodorovná, a proto stejné
členy
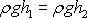 v rovnici
(4,103)
neuvádíme. Dle
rovnice kontinuity
(4,53)
v rovnici
(4,103)
neuvádíme. Dle
rovnice kontinuity
(4,53)
 . . |
Jelikož
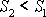 ,
musí být
,
musí být
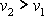 .
V průřezu
.
V průřezu
 je větší rychlost než v průřezu
je větší rychlost než v průřezu
 .
Potom
.
Potom
 a z
(4,103)
plyne
a z
(4,103)
plyne
 . . |
Menší tlak v průřezu
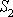 je na obr.74 naznačen menší výškou kapaliny
v připojené manometrické trubici u průřezu
je na obr.74 naznačen menší výškou kapaliny
v připojené manometrické trubici u průřezu
 .
Tlak v zúženém místě trubice může při větší rychlosti proudění klesnout až
pod okolní barometrický tlak a manometrickou trubicí je potom do kapaliny
nasáván vzduch. Na tomto principu jsou konstruovány vodní vývěvy, rozprašovače,
karburátory k benzinovým motorům a další zařízení. Aplikace Bernoulliovy
rovnice jsou velmi mnohostranné. Některé z nich jsou popsány v [6], čl.
2.5.2 a řada početních příkladů je uvedena v [8], kap. 9.
.
Tlak v zúženém místě trubice může při větší rychlosti proudění klesnout až
pod okolní barometrický tlak a manometrickou trubicí je potom do kapaliny
nasáván vzduch. Na tomto principu jsou konstruovány vodní vývěvy, rozprašovače,
karburátory k benzinovým motorům a další zařízení. Aplikace Bernoulliovy
rovnice jsou velmi mnohostranné. Některé z nich jsou popsány v [6], čl.
2.5.2 a řada početních příkladů je uvedena v [8], kap. 9.