Dosadíme-li do rovnice rovnováhy kontinua vyjádření napětí z (4,1) , dostaneme rovnici
kterou můžeme zapsat též v tvaru (srov. I, stať 3.4.4)
Objemová síla
 (viz
(1,76)
) je síla působící na jednotkový
objem. Síly, které dávají vznik objemovým silám působícím na tekutinu, typickou
takovou silou je tíže, jsou síly, jejichž velikost je úměrná hmotnosti objektu,
na který působí. Objemové síly
(viz
(1,76)
) je síla působící na jednotkový
objem. Síly, které dávají vznik objemovým silám působícím na tekutinu, typickou
takovou silou je tíže, jsou síly, jejichž velikost je úměrná hmotnosti objektu,
na který působí. Objemové síly
 jsou
tedy v tekutině úměrné hustotě
jsou
tedy v tekutině úměrné hustotě
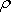 .
.
U kapalin je hustota
 konstantní a napíšeme-li rovnici
(4,7)
v tvaru
konstantní a napíšeme-li rovnici
(4,7)
v tvaru
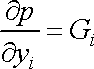 , , |
(4,7´´) |
můžeme její pravou stranu stanovit před řešením rovnice.
Hustota plynů je proměnná a závislá na tlaku
p. Když závislost vyjádříme
dle
(4,6)
, je pravá strana rovnice
(4,7´´)
funkcí tlaku a její hodnotu nelze
před řešením celé rovnice stanovit. Pro plyny je proto výhodnější místo
objemové síly
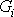 zavést do rovnice
(4,7´´)
intenzitu silového
pole (srov. I, čl.3.5), kterou označíme
zavést do rovnice
(4,7´´)
intenzitu silového
pole (srov. I, čl.3.5), kterou označíme
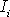 .
Intenzita silového pole je síla působící na jednotku hmotnosti tekutiny. Její
vztah k objemové síle je tedy
.
Intenzita silového pole je síla působící na jednotku hmotnosti tekutiny. Její
vztah k objemové síle je tedy
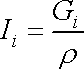 . . |
(4,8) |
Zavedeme-li do rovnice
(4,7´´)
intenzitu silového pole
(4,8)
, dostaneme po vydělení hustotou
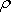 rovnici
rovnici
V této rovnici je možno i pro plyn stanovit explicitně pravou stranu již před řešením. Proto jí pro obecnou formulaci podmínek rovnováhy tekutin bývá dávána přednost před rovnicí (4,7) .
Rovnice (4,9) , a též její tvar (4,7) , se nazývá rovnice hydrostatické rovnováhy.
Řešením rovnice hydrostatické rovnováhy je stanovení funkce
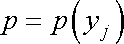 , , |
(4,10) |
která udává rozložení tlaku v tekutině. Funkce (4,10) plně charakterizuje stav kapaliny v rovnováze. U plynu je nutno ještě stanovit rozložení hustoty
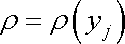 . . |
(4,11) |
Pro barotropní plyn funkci (4,11) získáme dosazením závislosti (4,10) do vyjádření hustoty (4,6) .
Z rovnice
(4,7)
nebo
(4,9)
plyne, že pro kapalinu (
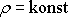 ) jsou parciální derivace
) jsou parciální derivace
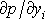 nezávislé na tlaku. Objemovými silami
nezávislé na tlaku. Objemovými silami
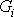 je rozložení tlaku v kapalině určeno až
na aditivní konstantu k. Je-li funkce
je rozložení tlaku v kapalině určeno až
na aditivní konstantu k. Je-li funkce
 řešením rovnice
(4,7)
, je jejím řešením také
každá funkce
řešením rovnice
(4,7)
, je jejím řešením také
každá funkce
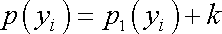 , , |
(4,12) |
kde k
je libovolná konstanta. Hodnota konstanty se stanoví z okrajových
podmínek konkrétního řešeného příkladu. Jelikož však jde o určení jediné
konstanty, redukují se okrajové podmínky na znalost tlaku p v jednom libovolném bodě kapaliny.
Změní-li se v tomto bodě tlak o hodnotu
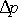 ,
změní se o stejnou hodnotu i konstanta k, a tedy i tlak v každém bodě kapaliny.
,
změní se o stejnou hodnotu i konstanta k, a tedy i tlak v každém bodě kapaliny.
Takto je v rovnici hydrostatické rovnováhy obsažen známý (např. [2] ) Pascalův zákon o všestranném šíření tlaku. Můžeme jej formulovat např. takto: Změna tlaku v jednom místě kapaliny způsobí stejnou změnu tlaku v celém objemu kapaliny, když před změnou i po změně je kapalina v rovnováze.
Vlastnost vystižená
Pascalovým zákonem je základem řady hydraulických zařízení, která užívají
kapaliny jako media k rozvádění síly. Známe hydraulické ovládaní brzd a
dalších prvků dopravních prostředků, hydraulické lisy a pod.
V hydraulických zařízeních přenášený tlak, odpovídající konstantě k z rovnice
(4,12)
, bývá velký ve
srovnání se změnami tlaku
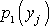 způsobenými objemovou, obvykle tíhovou
silou. V rovnici
(4,12)
můžeme funkci
způsobenými objemovou, obvykle tíhovou
silou. V rovnici
(4,12)
můžeme funkci
 zanedbat oproti konstantě k a
tlak p pokládat za konstantní a
rovný k v celém objemu
kapaliny.
zanedbat oproti konstantě k a
tlak p pokládat za konstantní a
rovný k v celém objemu
kapaliny.
Můžeme-li zanedbat působení objemových sil, je tlak ve všech bodech kapaliny stejný.
Z této poslední věty vychází při zjednodušeném výkladu činnosti zařízení aplikujících Pascalův zákon.
Na obr.58 je znázorněn princip hydraulického lisu. Silou o velikosti
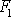 způsobíme v místě, kde se píst o
ploše
způsobíme v místě, kde se píst o
ploše
 stýká s kapalinou, tlak p o velikosti
stýká s kapalinou, tlak p o velikosti
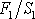 .
Dle poslední formulace Pascalova zákona pak předpokládáme stejný tlak p v celém objemu kapaliny, tedy i
v místě, kde se nachází píst
.
Dle poslední formulace Pascalova zákona pak předpokládáme stejný tlak p v celém objemu kapaliny, tedy i
v místě, kde se nachází píst
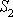 .
Má-li být kapalina v rovnováze, musí na píst
.
Má-li být kapalina v rovnováze, musí na píst
 působit síla o velikosti
působit síla o velikosti
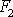 taková, aby tlak
taková, aby tlak
 byl roven
p. Musí tedy platit rovnice
byl roven
p. Musí tedy platit rovnice
 a pro poměr velikostí sil působících na
pístech o plochách
a pro poměr velikostí sil působících na
pístech o plochách
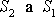 dostáváme
dostáváme
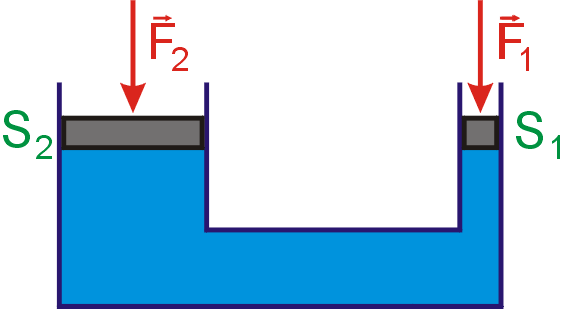
 .
(4,13)
.
(4,13)
Je-li plocha
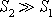 ,
bude
,
bude
 .
Působíme-li na píst
.
Působíme-li na píst
 malou silou
malou silou
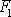 ,
získáme na pístu
,
získáme na pístu
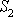 velkou sílu
velkou sílu
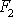 .
Stlačujeme-li píst
.
Stlačujeme-li píst
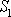 ,
posune se píst
,
posune se píst
 směrem vzhůru a stojí-li v jeho cestě
předmět opřený o pevnou podložku, je lisován velkou silou
směrem vzhůru a stojí-li v jeho cestě
předmět opřený o pevnou podložku, je lisován velkou silou
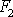 .
Velikost posunů
.
Velikost posunů
 pístu
pístu
 a
a
 pístu
pístu
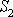 jsou v opačném poměru než velikosti
sil
jsou v opačném poměru než velikosti
sil
 ,
takže práce vykonané oběma písty jsou stejné;
,
takže práce vykonané oběma písty jsou stejné;
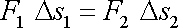 . . |
(4,14) |
Snadný rozvod tlaku a možnost získání velkých sil jsou důvody, pro které jsou hydraulická zařízení v technické praxi často užívána. Pro plyny platí Pascalův zákon ve zde vyložené formě pouze přibližně. Jeho přesnou formulaci pro případ barotropních plynů lze nalézt např. v [1], čl. 11.3.
Vyšetříme, jak se chová tekutina v tíhovém poli (tíhové pole viz I, čl. 4.2). Objemovou tíhovou sílu jsme uvažovali v čl. 3.6, když jsme studovali deformaci válce způsobenou jeho vlastní tíhou. Zvolíme-li stejně jako v čl. 3.6 první osu souřadnic ve svislém směru s kladným smyslem mířícím vzhůru, budou složky objemové tíhové síly dány rovnicemi (3,95)
 . . |
(3,95) |
Intenzita tíhového pole je pak dle (4,8)
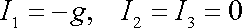 . . |
(4,15) |
Dosadíme-li (4,15) do (4,9) nebo (3,95) do (4,7) , dostáváme stejné rovnice
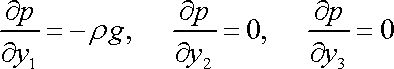 |
(4,16) |
pro určení hledané závislosti
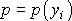 .
Z druhých dvou rovnic systému
(4,16)
plyne, že tlak p nezávisí na souřadnicích
.
Z druhých dvou rovnic systému
(4,16)
plyne, že tlak p nezávisí na souřadnicích
 ,
a je tedy funkcí pouze souřadnice
,
a je tedy funkcí pouze souřadnice
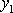 .
V první rovnici systému pak můžeme nahradit parciální derivaci úplnou
derivací;
.
V první rovnici systému pak můžeme nahradit parciální derivaci úplnou
derivací;
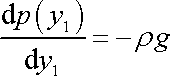 . . |
(4,17) |
Je-li tekutinou kapalina, je
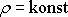 a řešením rovnice
(4,17)
dostáváme pro tlak
výraz
a řešením rovnice
(4,17)
dostáváme pro tlak
výraz
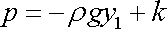 . . |
(4,18) |
Je-li tekutinou plyn, musíme do rovnice
(4,17)
dosadit
předpokládaný tvar
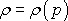 závislosti
(4,6)
. Rovnice
(4,17)
bude na
pravé straně obsahovat hledanou funkci p
a budeme ji tedy muset řešit jako rovnici diferenciální (viz postup za
rovnicí
(4,24)
).
závislosti
(4,6)
. Rovnice
(4,17)
bude na
pravé straně obsahovat hledanou funkci p
a budeme ji tedy muset řešit jako rovnici diferenciální (viz postup za
rovnicí
(4,24)
).
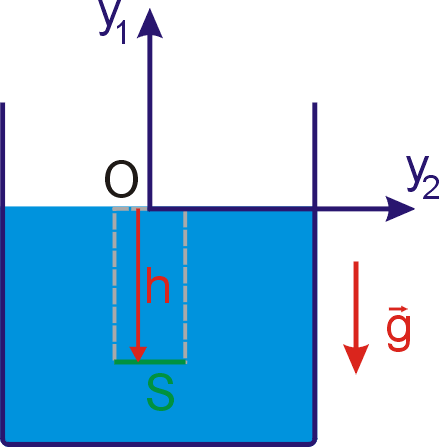 Rovnice
(4,18)
dává známý výraz pro hydrostatický
tlak v kapalinách. Na obr.59 je znázorněna kapalina v nádobě.
Počátek O souřadnicové soustavy uvažované při odvození rovnice
(4,18)
je
zvolen v hladině kapaliny. Hydrostatický tlak bývá zvykem udávat
v závislosti na hloubce h. Z obr.59 plyne, že
Rovnice
(4,18)
dává známý výraz pro hydrostatický
tlak v kapalinách. Na obr.59 je znázorněna kapalina v nádobě.
Počátek O souřadnicové soustavy uvažované při odvození rovnice
(4,18)
je
zvolen v hladině kapaliny. Hydrostatický tlak bývá zvykem udávat
v závislosti na hloubce h. Z obr.59 plyne, že
 a rovnici
(4,18)
můžeme přepsat na tvar
a rovnici
(4,18)
můžeme přepsat na tvar
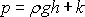 .
(4,19)
.
(4,19)
Z rovnice
(4,18)
nebo
(4,19)
plyne, že v hladině
kapaliny, kde
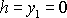 ,
je tlak p roven konstantě k;
,
je tlak p roven konstantě k;
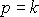 .
Na hladinu kapaliny působí z vnějšku barometrický tlak b,
tedy
.
Na hladinu kapaliny působí z vnějšku barometrický tlak b,
tedy
 .
Konstanta k v rovnicích
(4,18)
a
(4,19)
je v případě naznačeném na obr.59 rovna barometrickému tlaku b.
Při vyšetřování tlaku p
v kapalinách nás často zajímá pouze rozdíl
.
Konstanta k v rovnicích
(4,18)
a
(4,19)
je v případě naznačeném na obr.59 rovna barometrickému tlaku b.
Při vyšetřování tlaku p
v kapalinách nás často zajímá pouze rozdíl
 mezi tlakem
p a barometrickým tlakem b
a ne absolutní hodnota tlaku p. Pro rozdíl tlaků
mezi tlakem
p a barometrickým tlakem b
a ne absolutní hodnota tlaku p. Pro rozdíl tlaků
 ,
který někdy bývá přímo nazýván hydrostatickým tlakem a označovaným
jednoduše p (viz např. [2] ),
dostáváme pak výraz
,
který někdy bývá přímo nazýván hydrostatickým tlakem a označovaným
jednoduše p (viz např. [2] ),
dostáváme pak výraz
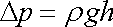 . . |
(4,20) |
Přesněji se rozdíl
 tlaku
p v určitém místě a okolního tlaku
tlaku
p v určitém místě a okolního tlaku
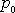 ,
kterým je často barometrický tlak b, nazývá přetlak. Je-li přetlak záporný, používá se v češtině pro jeho
absolutní hodnotu i název podtlak.
,
kterým je často barometrický tlak b, nazývá přetlak. Je-li přetlak záporný, používá se v češtině pro jeho
absolutní hodnotu i název podtlak.
K výrazu
(4,20)
lze dospět i elementárně. Myslíme-li si
v hloubce h v kapalině
plochu S rovnoběžnou
s hladinou, spočívá na této ploše vzhledem k nepřítomnosti smykových
napětí právě tíha
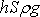 celého sloupce kapaliny nad touto plochou.
Vydělíme-li sílu
celého sloupce kapaliny nad touto plochou.
Vydělíme-li sílu
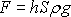 plochou
S, dostáváme pro tlak působící
na plochu S právě výraz
(4,20)
.
Jelikož v kapalině je na všech plochách procházejících daným bodem stejným
bodem stejný tlak, působí přetlak
plochou
S, dostáváme pro tlak působící
na plochu S právě výraz
(4,20)
.
Jelikož v kapalině je na všech plochách procházejících daným bodem stejným
bodem stejný tlak, působí přetlak
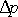 v hloubce h i na plochách, které nejsou rovnoběžné
s hladinou. Při elementárním odvození předpokládáme, že nad plochou S je kapalina až k hladině. Pro vznik
hydrostatického tlaku však takový předpoklad není nutný. Přetlak
v hloubce h i na plochách, které nejsou rovnoběžné
s hladinou. Při elementárním odvození předpokládáme, že nad plochou S je kapalina až k hladině. Pro vznik
hydrostatického tlaku však takový předpoklad není nutný. Přetlak
 daný rovnicí
(4,20)
vzniká v kapalině
v hloubce h ve všech místech, bez
ohledu na to, zda se nad nimi nachází kapalina nebo ne. Stačí si připomenout
v dřívější výuce vyložené případy hydrostatického paradoxu a spojitých
nádob.
daný rovnicí
(4,20)
vzniká v kapalině
v hloubce h ve všech místech, bez
ohledu na to, zda se nad nimi nachází kapalina nebo ne. Stačí si připomenout
v dřívější výuce vyložené případy hydrostatického paradoxu a spojitých
nádob.
Srovnáme chování kapaliny a pružného pevného tělesa
v tíhovém poli. Znamená to porovnat rovnice
(4,19)
s rovnicemi
(3,103)
. Nejpodstatnější rozdíl mezi oběma závislostmi je v tom, že
v kapalině všechna hlavní napětí, tj.
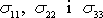 jsou rovna stejné hodnotě
jsou rovna stejné hodnotě
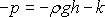 ,
zatímco v pružné pevné látce (v hookovské látce) napětí
,
zatímco v pružné pevné látce (v hookovské látce) napětí
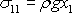 a
a
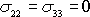 jsou podstatně různá.
jsou podstatně různá.
Barometrická rovnice
Závislost tlaku plynu na výšce v tíhovém poli lze
určit, předpokládáme-li nějaký konkrétní tvar funkce
(4,6)
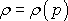 .
Nejjednodušší je předpokládat, že se plyn chová dle Boyleova-Mariottova zákona
( [3], kap. 4, [5], čl. 5.7, [51], čl. 2.5)
.
Nejjednodušší je předpokládat, že se plyn chová dle Boyleova-Mariottova zákona
( [3], kap. 4, [5], čl. 5.7, [51], čl. 2.5)
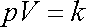 . . |
(4,21) |
V rovnici
(4,21)
V je měrný objem plynu a k
konstanta. Jelikož V
je měrný objem, je to objem, který zaujímá zcela určitý počet molekul
plynu. Označíme-li m úhrnnou hmotnost těchto
molekul, hustotu
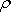 plynu můžeme vyjádřit jako
plynu můžeme vyjádřit jako
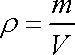 . . |
(4,22) |
Dosadíme-li z (4,22) za V do (4,21) , dostáváme
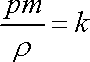 |
neboli
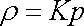 . . |
(4,23) |
V rovnici
(4,23)
jsme označili K konstantní výraz
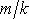 .
Rovnice
(4,23)
je konkrétní tvar funkce
(4,6)
odpovídající Boyleovu-Mariottovu
zákonu. Vyjádříme-li dle ní
.
Rovnice
(4,23)
je konkrétní tvar funkce
(4,6)
odpovídající Boyleovu-Mariottovu
zákonu. Vyjádříme-li dle ní
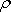 v rovnici
(4,17)
, dostáváme
v rovnici
(4,17)
, dostáváme
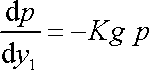 . . |
(4,24) |
Rovnice (4,24)
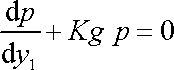 |
je lineární diferenciální rovnice prvního řádu s konstantními koeficienty bez pravé strany. Jejím obecným řešením je tedy funkce
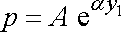 . . |
(4,25) |
Hodnotu
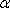 určíme řešením charakteristické rovnice
určíme řešením charakteristické rovnice
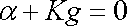 |
(4,26) |
a A
je volitelná konstanta, jejíž hodnotu lze určit z okrajové podmínky.
Řešením rovnice
(4,24)
je tedy závislost tlaku na výšce
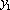 daná funkcí
daná funkcí
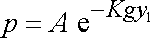 . . |
(4,27) |
Rovnice
(4,27)
bývá užívána k přibližnému vyjádření
závislosti tlaku vzduchu na výšce v atmosféře. V tomto případě se
počátek soustavy souřadnic volí u země, případně u hladiny moře. Je-li pro
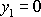 tlak
tlak
 ,
dostáváme dosazením této okrajové podmínky do rovnice
(4,27)
pro konstantu A hodnotu
,
dostáváme dosazením této okrajové podmínky do rovnice
(4,27)
pro konstantu A hodnotu
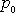 .
Je-li hustota plynu
.
Je-li hustota plynu
 pro
pro
 ,
můžeme dle
(4,23)
konstantu K vyjádřit jako
,
můžeme dle
(4,23)
konstantu K vyjádřit jako
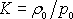 .
Rovnici
(4,23)
potom zapíšeme v tvaru
.
Rovnici
(4,23)
potom zapíšeme v tvaru
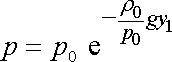 , , |
(4,28) |
kterému se říká barometrická
rovnice. Konstanty
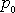 a
a
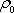 jsou rovny atmosférickému tlaku a hustotě
vzduchu, tedy
jsou rovny atmosférickému tlaku a hustotě
vzduchu, tedy
 a
a
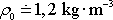 při
při
 .
Uvažujeme-li normální podmínky, dosadíme normální atmosférický tlak
.
Uvažujeme-li normální podmínky, dosadíme normální atmosférický tlak
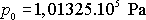 a hustotu suchého vzduchu při tomto tlaku a
teplotě
a hustotu suchého vzduchu při tomto tlaku a
teplotě
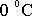
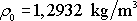 .
.
Boyllův-Mariottův zákon, který dle stavové rovnice ideálního
plynu ([3], kap. 4, [1], čl. 5.7, [51], čl. 2.5) platí pro izotermický děj, je
v atmosféře, kde teplota vzduchu s výškou klesá, splněn pouze
přibližně. Jak lze odvodit závislost tlaku plynu na výšce v tíhovém poli,
když uvažujeme obecnější závislost
(4,6)
 ,
než je přímá úměrnost
(4,23)
, je ukázáno např. v [1], čl. 11.3.
,
než je přímá úměrnost
(4,23)
, je ukázáno např. v [1], čl. 11.3.
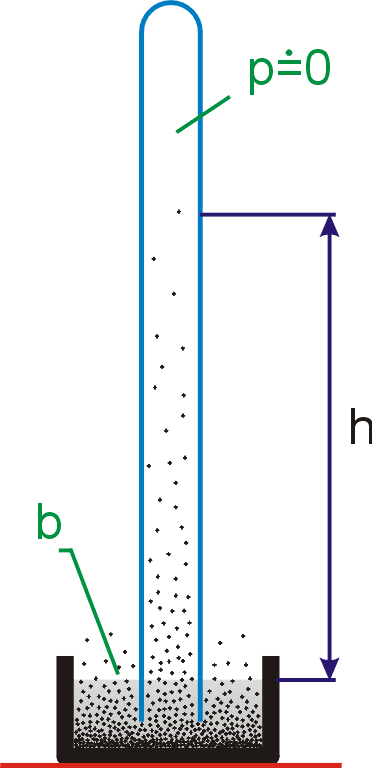
Existenci
atmosférického tlaku lze prokázat pokusem naznačeným na obr.60. Tento pokus
poprvé provedený v r. 1643 Torricellim je na jeho počest označován jako Torricelliův pokus. Tímto pokusem se
existence atmosférického tlaku dokáže tím, že tento tlak udrží ve skleněné trubici
na jednom konci zatavené sloupec rtuti o výšce
 .
Pokus se provádí tak, že trubice delší než asi
0,8 m se v poloze, kdy
zatavený konec je dole, naplní rtutí, horní konec se uzavře a trubice se
překlopí do nádobky s rtutí. Uzavření se pod hladinou rtuti uvolní,
přebytečná rtuť z trubice vyteče do nádobky a hladina rtuti se
v trubici ustálí ve výšce h, jak je naznačeno na obr.60. Nad rtutí
se v trubici ustálí zanedbatelný tlak nasycených rtuťových par, který
pokládáme za nulový. V hladině nádobky se tak vyrovná atmosférický
(barometrický) tlak b
s tlakem vyvolaným sloupcem rtuti o výšce h. Výška h měří aktuální atmosférický tlak v místě
nádobky.
.
Pokus se provádí tak, že trubice delší než asi
0,8 m se v poloze, kdy
zatavený konec je dole, naplní rtutí, horní konec se uzavře a trubice se
překlopí do nádobky s rtutí. Uzavření se pod hladinou rtuti uvolní,
přebytečná rtuť z trubice vyteče do nádobky a hladina rtuti se
v trubici ustálí ve výšce h, jak je naznačeno na obr.60. Nad rtutí
se v trubici ustálí zanedbatelný tlak nasycených rtuťových par, který
pokládáme za nulový. V hladině nádobky se tak vyrovná atmosférický
(barometrický) tlak b
s tlakem vyvolaným sloupcem rtuti o výšce h. Výška h měří aktuální atmosférický tlak v místě
nádobky.
Hydrostatický tlak vyvolaný 0,76 m vysokým sloupcem rtuti je
roven normálnímu atmosférickému tlaku,
tj. tlaku
 .
Milimetr rtuťového sloupce zvaný torr
byl dříve často užívanou jednotkou tlaku. Předminulá věta udává přepočtový
vztah mezi SI jednotkou pascal a jednotkou torr;
.
Milimetr rtuťového sloupce zvaný torr
byl dříve často užívanou jednotkou tlaku. Předminulá věta udává přepočtový
vztah mezi SI jednotkou pascal a jednotkou torr;
760 torr = 1,01325.105 Pa.
 Když
jsme v čl. 3.1 odvozovali rovnici rovnováhy kontinua, vyšli jsme
z podmínky, že kontinuum je v rovnováze, je-li v rovnováze každá
jeho část. Myslíme-li si v kontinuu jistý objem V (obr.61), výslednice
Když
jsme v čl. 3.1 odvozovali rovnici rovnováhy kontinua, vyšli jsme
z podmínky, že kontinuum je v rovnováze, je-li v rovnováze každá
jeho část. Myslíme-li si v kontinuu jistý objem V (obr.61), výslednice
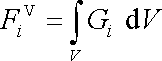 |
(4,29) |
objemových sil působících v tomto objemu musí být rovna záporně vzaté výslednici plošných sil
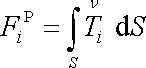 , , |
(4,30) |
které na objem V působí přes hraniční plochu S;
(eq0129).Je-li objemovou silou tíhová síla
(3,95)
, jediná nenulová
složka síly
 je
je
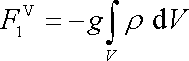 , , |
(4,32) |
a tedy dle rovnice (4,31)
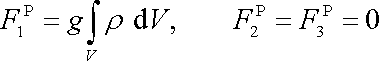 . . |
(4,33) |
Při zavedení objemové síly
(3,95)
byla první osa souřadnic
zvolena ve svislém směru s kladným smyslem mířícím vzhůru. Přes
plochu S působí na objem V kontinua které je v rovnováze a nachází
se v tíhovém poli, síla mířící vzhůru, jejíž velikost
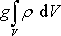 je rovna tíze kontinua obsaženého
v objemu V. Tato síla působí v každém kontinuu. Uvažujeme-li libovolnou
část válce z čl. 3.6, zjistíme, že na ni od okolních částí válce taková
síla působí.
je rovna tíze kontinua obsaženého
v objemu V. Tato síla působí v každém kontinuu. Uvažujeme-li libovolnou
část válce z čl. 3.6, zjistíme, že na ni od okolních částí válce taková
síla působí.
Zvláštní význam má zmíněná síla v tekutině. Tam totiž objem V může být vyplněn pevným tělesem, aniž se tím poruší rozložení napětí, tedy pro tekutinu tlaku. Na objem V vyplněný pevným tělesem pak od tekutiny působí přes hraniční plochu S stejné síly, jako kdyby objem V byl vyplněn tekutinou. Na pevné těleso, ponořené v tekutině, která je v tíhovém poli, působí síla (4,33) . Tato síla, které říkáme vztlak, míří svisle vzhůru a její velikost je rovna tíze stejného objemu V tekutiny, jako je objem ponořeného tělesa.
Dostáváme tak známý Archimedův zákon, který bývá formulován větou: Těleso ponořené do tekutiny je nadlehčováno silou, která je rovna tíze (váze) tekutiny tělesem vytlačené.
Mějme v nádobě kapalinu a v ní ponořený válec
(obr.62), jehož vrchní podstava je v hloubce
 a
spodní v hloubce
a
spodní v hloubce
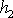 pod hladinou. Je-li plocha podstavy S,
působí na spodní podstavu síla o velikosti
pod hladinou. Je-li plocha podstavy S,
působí na spodní podstavu síla o velikosti
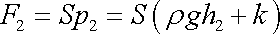 |
a na vrchní podstavu síla o velikosti
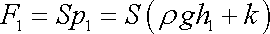 |
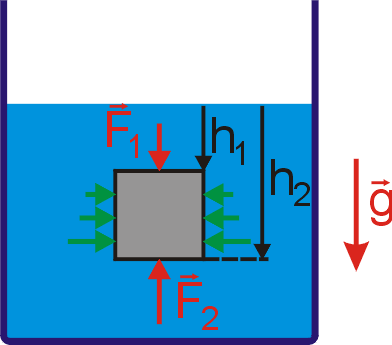 mířící
dolů. Tlak p je vyjádřen dle rovnice
(4,19)
. Síly působící na válcovou plochu mají v každé vrstvě rovnoběžné
s podstavou válce stejnou velikost a v protilehlých bodech ležících
na stejném průměru opačný smysl. Proto výsledná síla působící na válcovou
plochu je nulová. Velikost výsledné síly působící na celý ponořený válec je
tedy rovna rozdílu sil
mířící
dolů. Tlak p je vyjádřen dle rovnice
(4,19)
. Síly působící na válcovou plochu mají v každé vrstvě rovnoběžné
s podstavou válce stejnou velikost a v protilehlých bodech ležících
na stejném průměru opačný smysl. Proto výsledná síla působící na válcovou
plochu je nulová. Velikost výsledné síly působící na celý ponořený válec je
tedy rovna rozdílu sil
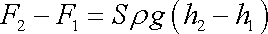 |
(4,34) |
a míří vzhůru. Výraz
 je roven objemu válce V a pro velikost vztlaku
je roven objemu válce V a pro velikost vztlaku
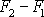 můžeme psát vyjádření
můžeme psát vyjádření
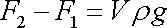 . . |
(4,35) |
Jelikož
 v rovnici
(4,35)
je hustota kapaliny a
ne hustota válce, vidíme, že velikost vztlaku je rovna tíze takového množství
kapaliny, které má objem rovný objemu válce
V. Uvedenou úvahou bývá
Archimedův zákon jednoduše dokazován (např. [2]).
v rovnici
(4,35)
je hustota kapaliny a
ne hustota válce, vidíme, že velikost vztlaku je rovna tíze takového množství
kapaliny, které má objem rovný objemu válce
V. Uvedenou úvahou bývá
Archimedův zákon jednoduše dokazován (např. [2]).
S Archimedovým zákonem se setkáme v různých aplikacích i při výkladu jevů kolem nás. Užívá se např. při zjišťování hustot látek (podrobněji viz [6] stať 2.1.4). Vztlak, kterým působí vzduch na vážený předmět, je třeba uvažovat při přesném vážení (např. [6], čl. 2.1.3.6). Let balónů a vzducholodí je umožněn v Archimédově zákoně uvažovanou statickou vztlakovou silou. Tělesa plovou na kapalině, když jejich průměrná hustota je menší než hustota kapaliny. Plováním těles se budeme podrobněji zabývat ve stati 4.2.4.
 Vyřešíme
příklad, kdy rovnici hydrostatické rovnováhy užijeme pro sledování rovnováhy
kapaliny v jiném než tíhovém poli objemových sil. Mějme kapalinu, která se
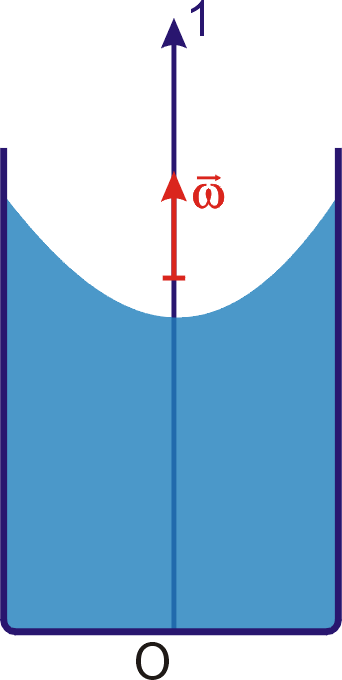
spolu s nádobou, v níž je umístěna, otáčí úhlovou rychlostí
Vyřešíme
příklad, kdy rovnici hydrostatické rovnováhy užijeme pro sledování rovnováhy
kapaliny v jiném než tíhovém poli objemových sil. Mějme kapalinu, která se
spolu s nádobou, v níž je umístěna, otáčí úhlovou rychlostí
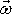 (obr.63). Vektor
(obr.63). Vektor
 leží ve svislé přímce. Zvolíme kartézskou
soustavu souřadnic pevně spjatou s kapalinou, jejíž první osa má směr
vektoru
leží ve svislé přímce. Zvolíme kartézskou
soustavu souřadnic pevně spjatou s kapalinou, jejíž první osa má směr
vektoru
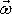 a míří vzhůru. Tato neinerciální soustava
souřadnic se otáčí stálou úhlovou rychlostí vůči soustavě inerciální. Dle I,
stať 2.4.2 v takové soustavě souřadnic vedle pravých sil působí zdánlivé
síly odstředivá a Coriolisova. Jediná působící pravá síla je objemová síla
tíhová, která ve zvolené soustavě souřadnic má složky
a míří vzhůru. Tato neinerciální soustava
souřadnic se otáčí stálou úhlovou rychlostí vůči soustavě inerciální. Dle I,
stať 2.4.2 v takové soustavě souřadnic vedle pravých sil působí zdánlivé
síly odstředivá a Coriolisova. Jediná působící pravá síla je objemová síla
tíhová, která ve zvolené soustavě souřadnic má složky
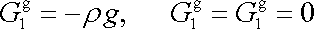 . . |
(4,36) |
Zdánlivá síla odstředivá, vyjádříme-li ji jako sílu
objemovou
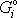 ,
je dána složkami
,
je dána složkami
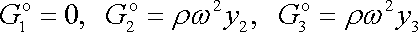 . . |
(4,37) |
Zdánlivá síla Coriolisova se neuplatní, protože kapalina se otáčí spolu s nádobou, a tedy rychlost částic kapaliny vůči neinerciální soustavě souřadnic je nulová.
Výslednou objemovou sílu
 dosadíme do pravé strany rovnice
(4,7´´)
;
dosadíme do pravé strany rovnice
(4,7´´)
;
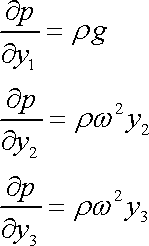 . . |
(4,38) |
Z prvé rovnice (4,38) plyne
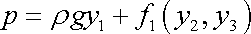 . . |
(4,39) |
Dosadíme-li toto vyjádření tlaku do druhé rovnice
(4,38)
,
dostáváme pro funkci
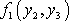 podmínku
podmínku
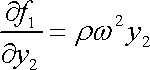 , , |
z které plyne
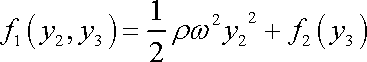 . . |
(4,40) |
Tedy
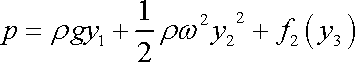 . . |
(4,41) |
Z poslední rovnice (4,38) pak dostáváme
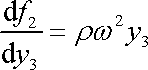 , , |
odkud
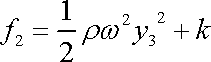 . . |
Dosadíme-li takto vyjádřenou funkci
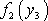 do rovnice
(4,41)
, dostaneme hledaný výraz
pro rozložení tlaku p
v rotující kapalině;
do rovnice
(4,41)
, dostaneme hledaný výraz
pro rozložení tlaku p
v rotující kapalině;
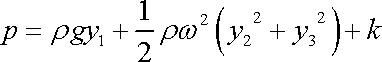 . . |
(4,42) |
Hodnotu konstanty k lze určit, je-li známa absolutní velikost tlaku v jednom bodě kapaliny. Plochy, v kterých kapalina nabývá stejného tlaku - takové plochy nazýváme hladinami - jsou v uvažovaném případě rotační paraboloidy
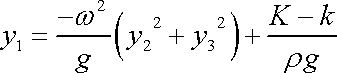 . . |
(4,43) |
Konstanta K
udává hodnotu tlaku p
v dané hladině. Jednotlivé hladiny se liší velikostí tlaku K
= p, a tedy i velikostí
konstanty
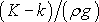 .
Jednou z hladin je také volná hladina
kapaliny[+],
tj. hladina, kde kapalina je v kontaktu se vzduchem. Na volné hladině
tlak p je roven atmosférickému
(barometrickému) tlaku b.
.
Jednou z hladin je také volná hladina
kapaliny[+],
tj. hladina, kde kapalina je v kontaktu se vzduchem. Na volné hladině
tlak p je roven atmosférickému
(barometrickému) tlaku b.
Otáčí-li se kapalina stálou úhlovou rychlostí kolem svislé osy, zaujme její volná hladina tvar rotačního paraboloidu. Na obr.63 je znázorněn řez otáčející se kapalinou a křivka znázorňující volnou hladinu je parabola. Dosáhnout toho, aby se kapalina v celém objemu nádoby otáčela stálou úhlovou rychlostí je dosti obtížné. Rozhodně toho nedosáhneme, když budeme míchat čaj v hrnku. V takovém případě kapalina lne ke stěnám nádobky a její úhlová rychlost stoupá od kraje hrnku ke středu. Výsledný tvar volné hladiny se pak blíží spíše nálevkovitému tvaru než rotačnímu paraboloidu. Přiblížit se rovnoměrné úhlové rotaci kapaliny, a tím i parabolickému tvaru volné hladiny, lze nejlépe, otáčíme-li nádobkou delší dobu stálou úhlovou rychlostí.
Plováním tělesa rozumíme děj, kdy těleso je částečně ponořeno v kapalině a částečně vyčnívá nad volnou hladinu kapaliny. Pro plování lodí je důležité, aby při malém vychýlení lodi z rovnovážné polohy vznikl moment síly, který je do rovnovážné polohy vrátí. Probereme nyní, jak lze zajistit takové podmínky nezbytné pro stabilní plování lodí. (Viz též řešený příklad 2, kap. 9 z [8].)
Těleso plove, když vztlak působící na plně ponořené těleso je větší než jeho tíha. V tom případě se těleso natolik vynoří z kapaliny, aby vztlak působící na jeho ponořenou část právě vyrovnal tíhu tělesa, tedy aby výslednice sil působící na těleso byla nulová. Aby došlo k rovnovážnému plování je ještě nutné, aby i výsledný moment sil působící na těleso byl nulový.
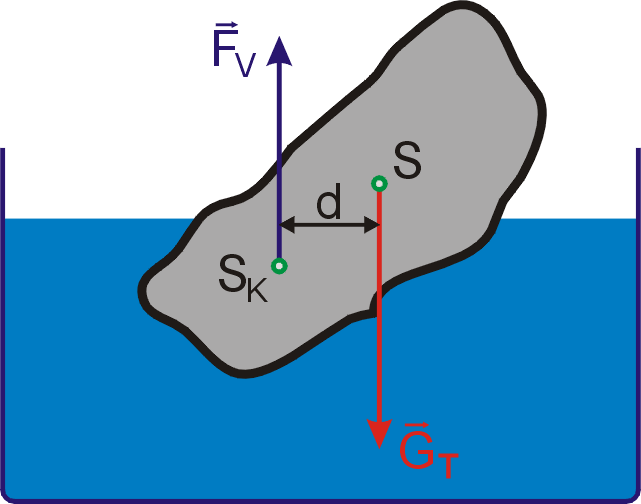 Na obr. 64 je zachyceno
těleso plovající na hladině v obecné, tedy nerovnovážné poloze.
V hmotném středu tělesa S na něj působí jeho tíže
Na obr. 64 je zachyceno
těleso plovající na hladině v obecné, tedy nerovnovážné poloze.
V hmotném středu tělesa S na něj působí jeho tíže
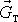 a v hmotném středu vytlačené
kapaliny SK vztlak
a v hmotném středu vytlačené
kapaliny SK vztlak
 .
V rovnováze musí výsledná síla i výsledný moment působící na těleso být
nulový, tedy
.
V rovnováze musí výsledná síla i výsledný moment působící na těleso být
nulový, tedy
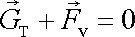 |
a
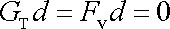 . . |
Z druhé rovnice, která udává, že výsledná dvojice sil
působící na těleso musí být nulová, plyne, že vzdálenost d přímek, v kterých působí síly
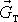 a
a
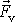 ,
musí být nulová. Vztlak a tíha musí při rovnovážném plování působit
v jedné svislé přímce, která se nazývá osa plování. Na ose plování musí tedy ležet jak hmotný střed
(těžiště) S tělesa tak i působiště vztlaku, kterým je hmotný střed
(těžiště) SK vytlačené kapaliny.
,
musí být nulová. Vztlak a tíha musí při rovnovážném plování působit
v jedné svislé přímce, která se nazývá osa plování. Na ose plování musí tedy ležet jak hmotný střed
(těžiště) S tělesa tak i působiště vztlaku, kterým je hmotný střed
(těžiště) SK vytlačené kapaliny.
Je-li těleso homogenní a symetrické, pak každá geometrická osa symetrie tělesa může teoreticky být osou plování. Skutečné plování však nastane jen pro tu osu plování, vůči které je plování stabilní nebo indiferentní (srov. I, str. 162). Plování tělesa je stabilní, když při jakémkoliv vychýlení plovoucího tělesa z jeho rovnovážné polohy dvojice sil tvořená vztlakem a tíhou tělesa se snaží těleso vrátit do jeho rovnovážné polohy. Plování tělesa je indiferentní, když při vychýlení tělesa z rovnovážné polohy nevzniká žádný moment síly.
 Plování desky je stabilní, když plove na
hladině svou širokou stranou, plování na úzkých stranách je labilní a nelze je proto realizovat.
Plování homogenní koule je indiferentní, všechny přímky procházející středem
koule mohou být osami plování. Plování homogenního válce je indiferentní pro
rotaci kolem osy válce.
Plování desky je stabilní, když plove na
hladině svou širokou stranou, plování na úzkých stranách je labilní a nelze je proto realizovat.
Plování homogenní koule je indiferentní, všechny přímky procházející středem
koule mohou být osami plování. Plování homogenního válce je indiferentní pro
rotaci kolem osy válce.
 Obecně
můžeme stabilitu plování vyšetřovat, najdeme-li v tělese plochu, na níž
leží působiště vztlaku pro různá natočení plovoucího tělesa, tato plocha se
nazývá plocha těžišť. Těžištěm se
zde míní těžiště kapaliny vytlačené tělesem na obr.64 označené
Obecně
můžeme stabilitu plování vyšetřovat, najdeme-li v tělese plochu, na níž
leží působiště vztlaku pro různá natočení plovoucího tělesa, tato plocha se
nazývá plocha těžišť. Těžištěm se
zde míní těžiště kapaliny vytlačené tělesem na obr.64 označené
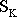 .
Na obr.65 jsou vyznačeny řezy kvádrem vedené jeho geometrickým a vzhledem
k předpokládané homogenitě i hmotným středem S kolmo ke dvěma jeho
hranám. Na řezech (řezy takto vedené označujeme jako hlavní řezy) jsou
vyznačeny jejich průsečnice p
s plochou těžišť. Je vidět, že při vychýlení kvádru z plování na
širší straně silová dvojice tíhy
.
Na obr.65 jsou vyznačeny řezy kvádrem vedené jeho geometrickým a vzhledem
k předpokládané homogenitě i hmotným středem S kolmo ke dvěma jeho
hranám. Na řezech (řezy takto vedené označujeme jako hlavní řezy) jsou
vyznačeny jejich průsečnice p
s plochou těžišť. Je vidět, že při vychýlení kvádru z plování na
širší straně silová dvojice tíhy
 působící v hmotném středu tělesa S a
vztlaku
působící v hmotném středu tělesa S a
vztlaku
 vede k obnovení plování na širší straně
kvádru (obr.65 a) ), v případě
plování na užší straně táž silová dvojice (obr.65b)) kvádr převrátí. Plování na širší straně kvádru je
realizovatelné stabilní plování, na užší straně nelze pro labilitu plování
realizovat.[span> Vztlaková
síla
vede k obnovení plování na širší straně
kvádru (obr.65 a) ), v případě
plování na užší straně táž silová dvojice (obr.65b)) kvádr převrátí. Plování na širší straně kvádru je
realizovatelné stabilní plování, na užší straně nelze pro labilitu plování
realizovat.[span> Vztlaková
síla
 působí v těžišti ponořené části kvádru,
tedy v bodu plochy těžišť, který přísluší danému naklonění kvádru. Vztlak
míří svisle vzhůru a je kolmý k průsečnici p.
působí v těžišti ponořené části kvádru,
tedy v bodu plochy těžišť, který přísluší danému naklonění kvádru. Vztlak
míří svisle vzhůru a je kolmý k průsečnici p.
Na obr.66 jsou znázorněny silové poměry při plování
homogenní koule. Zde tíha
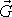 a vztlak
a vztlak
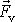 působí při libovolném natočení v jedné
přímce. Průsečnice p je totiž kružnice se
středem v hmotném středu koule S,
a tedy vztlak musí působit podél přímky procházející působištěm tíhy. Obr.66 platí beze změny i pro hlavní řez válcem
vedený kolmo k jeho ose symetrie. Rovnováha při plování koule a při
plování válce pro rotaci kolem osy je indiferentní. Dostat se z vody na
kládu nebo míč je obtížné, protože když se snažíme na ně vylézt, neustále se
otáčejí.
působí při libovolném natočení v jedné
přímce. Průsečnice p je totiž kružnice se
středem v hmotném středu koule S,
a tedy vztlak musí působit podél přímky procházející působištěm tíhy. Obr.66 platí beze změny i pro hlavní řez válcem
vedený kolmo k jeho ose symetrie. Rovnováha při plování koule a při
plování válce pro rotaci kolem osy je indiferentní. Dostat se z vody na
kládu nebo míč je obtížné, protože když se snažíme na ně vylézt, neustále se
otáčejí.
Pro vystižení míry stability rotace se zavádí pojem metacentrum. Metacentra se obvykle
definují (např. [1],
str.378) jako středy křivosti hlavních normálových řezů plochy těžišť
v místě, kde ji osa plování o
protíná. Na obr.67 jsou vyznačena metacentra M pro znázorněné hlavní
řezy kvádru. Pro kvádr plovoucí na šířku je užito označení
 a pro příslušnou osu plování
a pro příslušnou osu plování
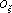 ,
pro kvádr plovoucí na výšku
,
pro kvádr plovoucí na výšku
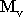 a
a
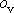 .
Pro libovolný řez homogenní koulí či řez homogenním válcem kolmo k rotační
ose (hlavní řez) je metacentrum ve středu kružnice, kterou tvoří průsečnice
plochy těžišť s hlavním řezem. Metacentrum M v tomto případě
padne do hmotného středu (těžiště) tělesa
S, jak je také naznačeno v obr.67. Metacentrum pro druhý hlavní řez
válce spadá do nekonečna. I zde shora uvedenou definici je třeba brát
s rezervou vyplývající z předchozí poznámky pod čarou. Metacentrum je
nutno brát jako střed kružnice, která nejlépe aproximuje průsečnici v ne
příliš malém okolí bodu, kde osa plování protíná průsečnici, a ne striktně jako
střed křivosti průsečnice v tomto bodě. Metacentrum pro konečný válec také
neleží v nekonečnu, ale v konečnu. Kládu lze ve vodě přetočit kolem příčné
osy, i když obtížně.
.
Pro libovolný řez homogenní koulí či řez homogenním válcem kolmo k rotační
ose (hlavní řez) je metacentrum ve středu kružnice, kterou tvoří průsečnice
plochy těžišť s hlavním řezem. Metacentrum M v tomto případě
padne do hmotného středu (těžiště) tělesa
S, jak je také naznačeno v obr.67. Metacentrum pro druhý hlavní řez
válce spadá do nekonečna. I zde shora uvedenou definici je třeba brát
s rezervou vyplývající z předchozí poznámky pod čarou. Metacentrum je
nutno brát jako střed kružnice, která nejlépe aproximuje průsečnici v ne
příliš malém okolí bodu, kde osa plování protíná průsečnici, a ne striktně jako
střed křivosti průsečnice v tomto bodě. Metacentrum pro konečný válec také
neleží v nekonečnu, ale v konečnu. Kládu lze ve vodě přetočit kolem příčné
osy, i když obtížně.
 Každá plocha má v daném místě dva hlavní
řezy. To platí samozřejmě i pro plochu těžišť, a proto i metacentra příslušná
místu, kde ji osa plování protíná jsou dvě. Pro stabilní plování podél dané osy
plování je nutné, aby obě metacentra ležela nad hmotným středem (těžištěm)
plovoucího tělesa. Menšímu z obou převýšení metacentra nad hmotným středem
říkáme metacentrická výška.
Každá plocha má v daném místě dva hlavní
řezy. To platí samozřejmě i pro plochu těžišť, a proto i metacentra příslušná
místu, kde ji osa plování protíná jsou dvě. Pro stabilní plování podél dané osy
plování je nutné, aby obě metacentra ležela nad hmotným středem (těžištěm)
plovoucího tělesa. Menšímu z obou převýšení metacentra nad hmotným středem
říkáme metacentrická výška.
Metacentrická výška udává míru stability plování tělesa; čím je větší, tím je plování stabilnější. Pro plování s indiferentní rovnováhou (válec, koule) je metacentrická výška nulová. Hodnota metacentrické výšky hraje důležitou roli při konstruování lodí. Zvláště sportovní lodě, které mají plout v bouřlivém prostředí otevřeného moře, vybavujeme těžkými kýly. Kýl sníží polohu těžiště a tím zvýší metacentrickou výšku plavidla. Metacentrická výška námořních dopravních lodí činí asi 0,3 m, u válečných lodí i více než 1 m. Metacentrická výška je obvykle trojnásobkem až pětinásobkem vzdálenosti hmotného středu od plochy těžišť.