---

---

3.5 Ohyb

Ohybem rozumíme deformaci tyčí silami kolmými k jejich podélné ose. Z praktického hlediska je ohyb tyče velmi důležitým typem deformace. Tyče ohybově namáhané, říkáme jim v této souvislosti nosníky, jsou součástmi nejrůznějších konstrukcí. Přesné vyšetření ohybu z hlediska klasické teorie pružnosti je obtížné. Při vyšetřování ohybu se často užívá zjednodušená teorie označovaná někdy jako technická pružnost. Ta vychází z některých ne zcela přesně splněných předpokladů, např. předpokládá, že příčný průřez ohýbané tyče zůstává rovinným. Takové předpoklady značně zjednoduší řešení úlohy, přičemž odchylky od nesrovnatelně složitějšího přesného řešení bývají zanedbatelné. Ukážeme, jak se dle této zjednodušené teorie vyšetřuje ohyb vetknutého nosníku.

3.5.1 Ohyb vetknutého nosníku

Vetknutý nosník je znázorněn na obr.52. Tyč, jejíž jeden konec je pevně spojený se stěnou S, je na opačném konci zatížena silou . V zjednodušeném rozboru (viz např. [4], čl. 2.6.8 ) se uvažuje pouze moment síly vytvořený silou 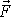a ne její smykový účinek. Činí se předpoklad, který ve skutečnosti není splněn, že všechny body ležící před deformací v jedné rovině kolmé k ose tyče zůstávají body jedné roviny kolmé k ose tyče i po deformaci. Dále budeme stejně jako v předcházejících úlohách řešených klasickou teorií pružnosti zanedbávat vlastní tíhu nosníku.

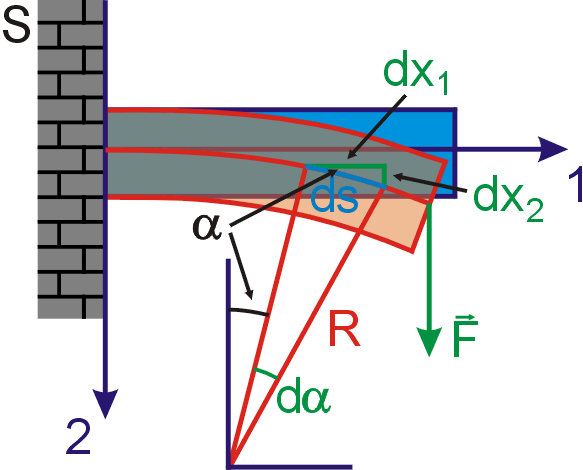
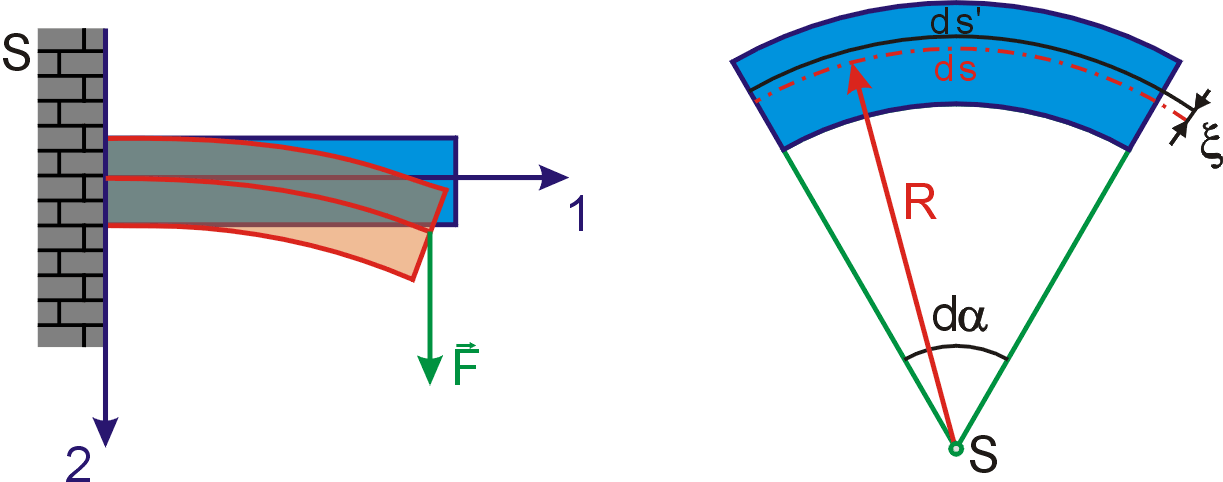Na obr.53 je znázorněn elementární úsek ohnuté tyče mezi dvěma rovinnými průřezy. Jelikož rovinné průřezy byly rovinnými a kolmými k ose tyče i před ohnutím, je vrchní část tyče ohybem protažena a spodní část stlačena. Mezi oběma částmi tyče leží rovina, v níž podélná deformace je nulová. Tuto rovinu, jejíž průmět je na obr.53 znázorněn čárkovaně, budeme nazývat neutrální rovinou. Pro elementární úsek tyče předpokládáme, že je ohnut do kruhového oblouku; poloměr tohoto oblouku měřený k neutrální rovině značíme R. Délka elementu ds měřená v nedeformované neutrální rovině je

.

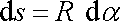Délka 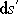elementu vlákna ležícího v rovině tyče vzdálené 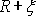od středu křivosti S vlákna je

.

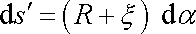Před deformací byla délka elementu takového vlákna ds. Relativní prodloužení (pro 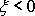se jedná o stlačení) elementu vlákna neboli jeho podélná deformace

.

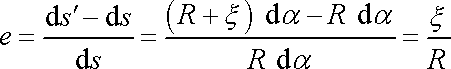(3,77)

Při vyšetřování deformace vztahujeme v klasické teorii pružnosti všechny úvahy k nedeformovanému stavu tělesa. V souřadnicové soustavě zvolené na obr.52 budeme předpokládat, že první osa souřadnic leží v neutrální rovině. Potom deformace e daná rovnicí (3,77) je složkou 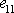tenzoru deformace a 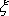znázorněné na obr.53 je rovno 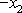(kladný smysl osy 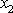volíme svisle dolů). Pro složku 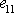tenzoru deformace v ohnutém nosníku tak dostáváme vyjádření

.

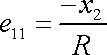(3,78)

Dle Hookova zákona pro tah ( (3,29) s uvážením (3,32) ) přiřazujeme deformaci (3,78) napětí

.

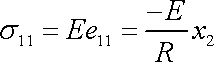(3,79)

O ostatních složkách napětí budeme předpokládat, že jsou nulové, i když na konci nosníku tento předpoklad zřejmě odporuje okrajovým podmínkám.

Síla 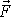působící na konci nosníku, který má délku l, vytvoří v průřezu tyče vzdáleném 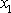od stěny S moment o velikosti

.

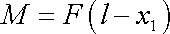(3,80)

Tento moment musí být roven momentu sil, který v průřezu vytváří napětí (3,79) . Velikost momentu, který napětí 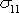vytváří vůči ose dané průsečíkem uvažovaného průřezu a neutrální roviny (rovina 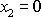), je

.

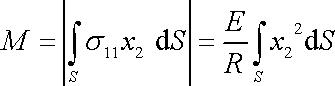(3,81)

Integrace probíhá přes celou plochu S průřezu. Velikost výrazu 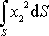je určena velikostí a tvarem plochy průřezu. Tato veličina se nazývá kvadratický moment průřezu nebo též osový kvadratický moment průřezu[+] a značí se ;

.

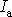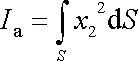(3,82)

S označením 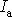je možno rovnici (3,81) zapsat ve stručném tvaru

.

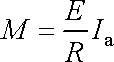(3,83)

Z výrazu (3,83) plyne, že při dané hodnotě M a E je R tím větší, čím větší je 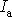. Je-li kvadratický moment průřezu tyče větší, nosník se méně ohne. Větší kvadratické momenty mají při stejné celkové velikosti plochy průřezu nosníky, jejichž plocha je soustředěna ve větších vzdálenostech od neutrální roviny. Proto bývají v praxi oblíbeny nosníky s průřezem ve tvaru písmen T a I .

Průsečnici neutrální plochy s rovinou 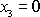říkáme neutrální vlákno. V rámci uvažovaného přiblížení určíme tvar ohnutého nosníku, stanovíme-li ohnutí neutrálního vlákna. Rovnici neutrálního vlákna zapíšeme jako funkční závislost (viz obr.54 )

.

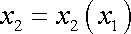(3,84)

Při malém ohybu nosníku, který předpokládáme, platí přibližný vztah

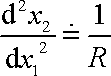(3,85)

mezi druhou derivací funkce (3,84) a poloměrem křivosti R křivky. Pro křivku danou rovnicí 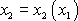je poloměr křivosti R dán výrazem

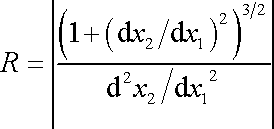(viz např. [9], čl. 9.4), který pro malé ohnutí neutrálního vlákna, kde derivace 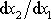je malá, dává uvažované přibližné vyjádření 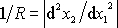. Absolutní hodnota ve výrazu pro 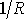zaručuje kladnou hodnotu R. Při úvahách o ohybu nosníku absolutní hodnotu vynecháme, změna znaménka výrazu 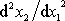nás upozorní na změnu smyslu ohybu nosníku. Vztah (3,85) lze objasnit i z obr.54, dle kterého platí

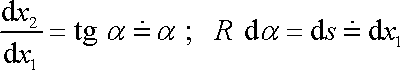(3,86)

neboli

.

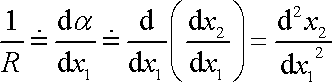V rovnici (3,83) je moment M funkcí souřadnice 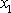. Dosadíme-li do (3,83) vyjádření 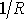dle (3,85) , dostáváme diferenciální rovnici

(3,87)

pro hledanou funkci (3,84) . Rovnice (3,87) je základní rovnicí zde vyložené zjednodušené teorie ohybu tyčí. Pro známý průběh momentu síly M podél délky tyče získáme řešením rovnice (3,87) tvar neutrálního vlákna v ohnuté tyči.

Moment síly 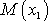vetknutého nosníku je dán funkcí (3,80) . Dosadíme-li ji do rovnice (3,87) , dostaneme

.

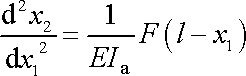(3,88)

Rovnici (3,88) lze přímo integrovat;

.

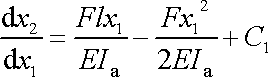(3,89)

Derivace 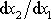udává směr tečny neutrálního vlákna. Ze způsobu vetknutí nosníku (viz obr.54) plyne 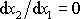pro 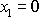, a tedy 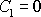. Další integrací rovnice (3,89) dostáváme

.

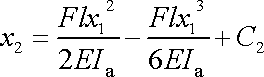(3,90)

Konstantu 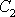opět položíme rovnu nule, protože pro 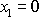musí být i 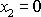. Tvar neutrálního vlákna vetknutého nosníku je v uvažovaném přibližném vyjádření dán rovnicí

.

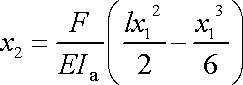(3,91)

Dosadíme-li l za 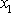do (3,91) , dostáváme pro posunutí 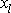volného konce nosníku ve směru působící síly vyjádření

.

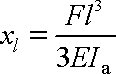(3,92)

3.5.2 Další druhy ohybu nosníků

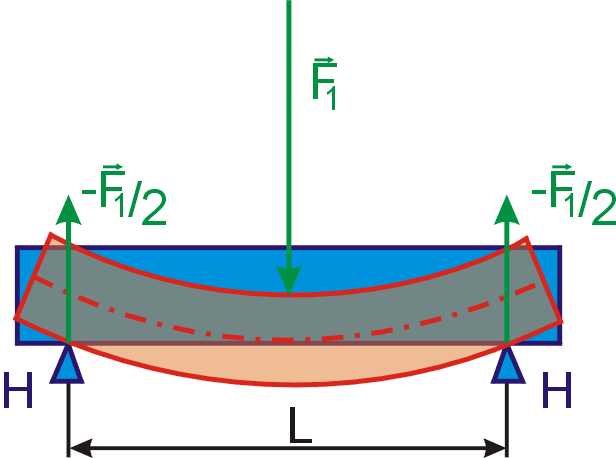Poslední výraz lze užít i pro výpočet průhybu d nosníku uloženého na dvou oporách vzdálených od sebe o délku L, který je uprostřed zatížen osamělou silou 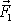(obr.55). Na podpěrných hrotech H působí vzhledem k symetrii problému síly o velikosti 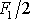. V místě, kde působí síla 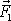, má nosník vodorovnou tečnu a uvažujeme-li půlku nosníku, jsou pro ni geometrické podmínky stejné jako u vetknutého nosníku. Pro výpočet průhybu d pak užijeme vzorec (3,92) , kam za délku l dosadíme 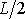a za F sílu 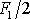; dostáváme

.

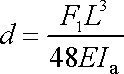(3,93)

Jak jsme již uvedli, lze vzorec (3,87) užít i pro jiné závislosti , než je závislost daná rovnicí (3,80) . Předpokládáme-li 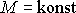, mluvíme o čistém ohybu a z (3,87) dostáváme pro tvar neutrálního vlákna rovnici

.

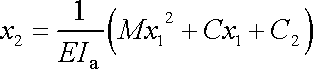(3,94)

Dle (3,85) parabolická závislost (3,94) vede na konstantní křivost nosníku, 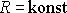, což ovšem při 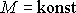plyne též přímo z rovnice (3,83) .

 

V obecném případě zahrnujeme do moment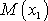u příspěvky různě rozložených vnějších sil působících na nosník i působení vlastní tíhy nosníku (viz [4], [13], [16] ). Některé případy ohybu lze přesně řešit teorií pružnosti, aniž užíváme zde vyložených zjednodušených představ. Řešení čistého ohybu a ohybu vetknutého nosníku lze nalézt v [1] a [17]. V těchto řešeních je ukázáno, že ve skutečnosti při ohybu dochází ke zborcení rovin původně kolmých k ose nosníku.

 

---

---