Budeme nyní vyšetřovat deformaci tělesa, u něhož nezanedbáme
vlastní tíhu. Aby řešení bylo jednoduché, zvolíme homogenní (hustota
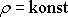 ) kruhový válec upevněný tak, že jeho osa má
směr tíhové síly
) kruhový válec upevněný tak, že jeho osa má
směr tíhové síly
 a bod
S, kde osa protíná vrchní podstavu (střed vrchní podstavy), je upevněn.
Osou válce proložíme první osu souřadnic, počátek souřadnicové soustavy zvolíme
ve středu spodní podstavy, směr druhé a třetí osy souřadnic v rovině
a bod
S, kde osa protíná vrchní podstavu (střed vrchní podstavy), je upevněn.
Osou válce proložíme první osu souřadnic, počátek souřadnicové soustavy zvolíme
ve středu spodní podstavy, směr druhé a třetí osy souřadnic v rovině
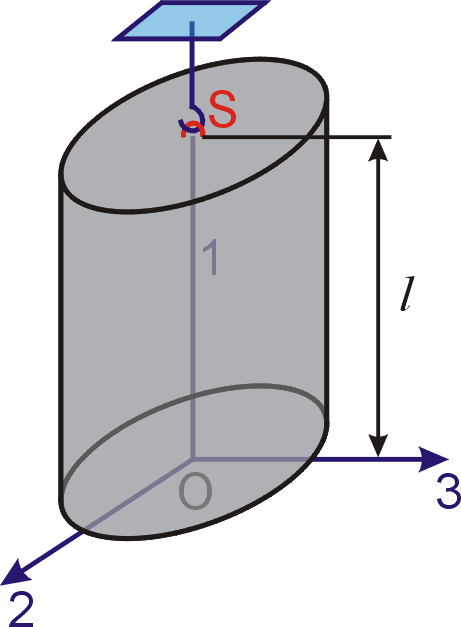 podstavy je libovolný
(obr.56). Vnější síly působící na válec jsou objemová tíhová síla
podstavy je libovolný
(obr.56). Vnější síly působící na válec jsou objemová tíhová síla
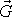 o složkách
o složkách
 |
(3,95) |
a plošné síly na povrchu válce. Na spodní podstavě a na
válcové ploše jsou vnější plošné síly, tedy i příslušné vektory napětí
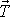 nulové. Na vrchní podstavě válce působí
v bodě závěsu síla
nulové. Na vrchní podstavě válce působí
v bodě závěsu síla
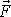 mířící ve směru a smyslu osy
mířící ve směru a smyslu osy
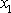 .
Její velikost je
.
Její velikost je
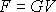 ,
kde V je objem válce. Dle Saint- Venantova
principu zaměníme toto diskrétní rozložení sil na vrchní podstavě rozložením
pro výpočet jednodušším. Budeme předpokládat, že na vrchní podstavě působí
napěťový vektor konstantní velikosti
,
kde V je objem válce. Dle Saint- Venantova
principu zaměníme toto diskrétní rozložení sil na vrchní podstavě rozložením
pro výpočet jednodušším. Budeme předpokládat, že na vrchní podstavě působí
napěťový vektor konstantní velikosti
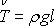 mířící vzhůru. Velikost celkové síly
působící na vrchní podstavu
mířící vzhůru. Velikost celkové síly
působící na vrchní podstavu
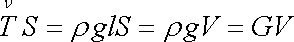 |
je shodná s velikostí síly F. Na povrchu válce tedy působí napěťové vektory o složkách
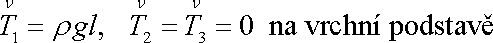 , , |
(3,96) |
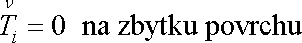 . . |
(3,97) |
Okrajové podmínky
(3,14)
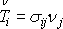 lze rozebrat podobně jako v čl. 3.3 a
plyne z nich
lze rozebrat podobně jako v čl. 3.3 a
plyne z nich
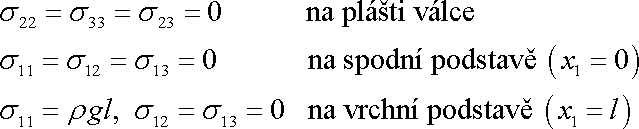 . . |
(3,98) |
Dosadíme-li do rovnice rovnováhy kontinua (3,8) objemovou sílu (3,95) , dostaneme
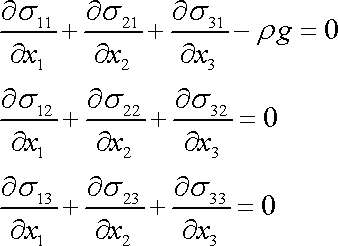 . . |
(3,99) |
Předpokládáme, že
 různá od
různá od
 ,
která jsou nulová na hraničních plochách válce, jsou nulová v celém objemu
válce. Potom jsou druhé dvě rovnice systému
(3,99)
splněny identicky a první
rovnice dává
,
která jsou nulová na hraničních plochách válce, jsou nulová v celém objemu
válce. Potom jsou druhé dvě rovnice systému
(3,99)
splněny identicky a první
rovnice dává
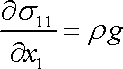 . . |
(3,100) |
Z rovnice
(3,100)
dostáváme pro jedinou nenulovou
složku
 tenzoru napětí vyjádření
tenzoru napětí vyjádření
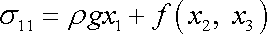 . . |
(3,101) |
Dle
(3,98)
má být
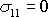 pro všechny body spodní podstavy, tj.
pro
pro všechny body spodní podstavy, tj.
pro
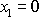 a libovolné
a libovolné
 splňující podmínku
splňující podmínku
 ,
kde R je poloměr podstavy válce. Na vrchní
podstavě, tj. pro body
,
kde R je poloměr podstavy válce. Na vrchní
podstavě, tj. pro body
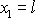 a
a
 splňující podmínku
splňující podmínku
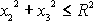 je
je
 .
Máme-li vyhovět těmto podmínkám, musíme položit v
(3,101)
.
Máme-li vyhovět těmto podmínkám, musíme položit v
(3,101)
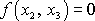 ;
tedy
;
tedy
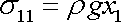 . . |
(3,102) |
Napětí dané složkami
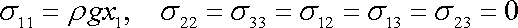 |
(3,103) |
splňuje podmínky rovnováhy
(3,8)
a okrajové podmínky
(3,14)
.
Splňuje i podmínky kompatibility ([1], čl. 5.5). Jelikož lze dokázat, že úloha nalézt napětí
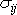 vyhovující právě uvedeným podmínkám má
jednoznačné řešení (viz např. [1], čl. 6.5), je
(3,103)
hledaným napětím ve
vyšetřovaném válci.
vyhovující právě uvedeným podmínkám má
jednoznačné řešení (viz např. [1], čl. 6.5), je
(3,103)
hledaným napětím ve
vyšetřovaném válci.
Najdeme deformace příslušné napětím
(3,103)
. Dosadíme-li
složky napětí
(3,103)
do Hookova zákona
(2,8)
, dostáváme stejné rovnice
(3,20)
jako v případě tahu. Pro získání složek deformace z rovnic
(3,20)
není podstatné, že nyní
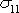 je funkcí
je funkcí
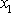 a v rovnicích
(3,20)
bylo konstantní.
Algebraický postup, který jsme užili při řešení rovnic
(3,20)
, z něhož
plynulo
a v rovnicích
(3,20)
bylo konstantní.
Algebraický postup, který jsme užili při řešení rovnic
(3,20)
, z něhož
plynulo
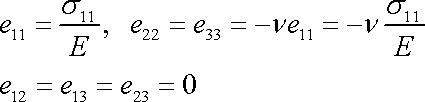 , , |
(3,104) |
zůstává v platnosti i nyní (
 je Poissonův poměr
(3,24)
). Deformace
vyvolané v uvažovaném válci jeho vlastní tíhou jsou dány tenzorovou funkcí
(3,104)
. Dosadíme-li do ní za
je Poissonův poměr
(3,24)
). Deformace
vyvolané v uvažovaném válci jeho vlastní tíhou jsou dány tenzorovou funkcí
(3,104)
. Dosadíme-li do ní za
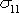 z
(3,103)
, dostaneme explicitní vyjádření
z
(3,103)
, dostaneme explicitní vyjádření
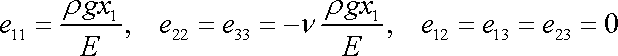 . . |
(3,105) |
Ze složek tenzoru deformace stanovíme vektor posunutí
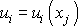 postupem, který jsme již také užili při
vyšetřování tahu v čl. 3.3. Z rovnic
(1,31)
postupem, který jsme již také užili při
vyšetřování tahu v čl. 3.3. Z rovnic
(1,31)
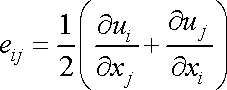 |
dostáváme
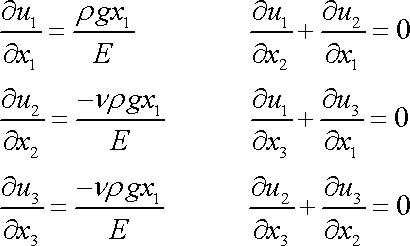 . . |
(3,106) |
Z rovnic na levé straně systému (3,106) plyne
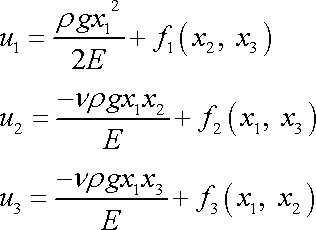 . . |
(3,107) |
První z rovnic na pravé straně systému
(3,106)
po
dosazení
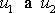 z
(3,107)
dává
z
(3,107)
dává
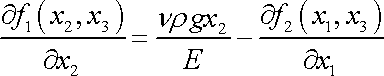 . . |
(3,108) |
Je-li na levé straně rovnice funkce proměnných
 ,
může
,
může
 být funkcí pouze
být funkcí pouze
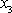 ;
;
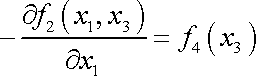 . . |
(3,109) |
Integrací rovnice (3,108) potom dostáváme
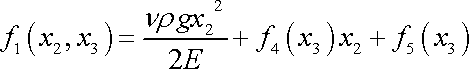 . . |
(3,110) |
Z druhé rovnice na pravé straně systému (3,106) , dosadíme-li do ní z (3,107) , plyne
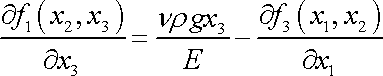 . . |
(3,111) |
Znovu musí být
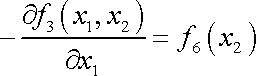 |
(3,112) |
a integrací (3,111) dostáváme
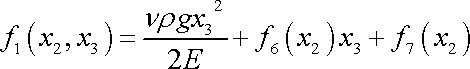 . . |
(3,113) |
Z (3,109) a (3,112) plyne
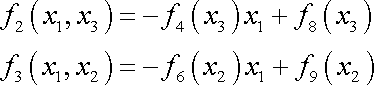 . . |
(3,114) |
Z poslední rovnice pravé strany systému (3,106) pak s uvážením (3,107) dostáváme
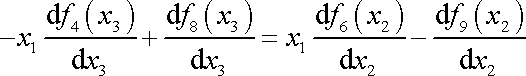 . . |
(3,115) |
Poslední rovnice může být splněna pouze, když
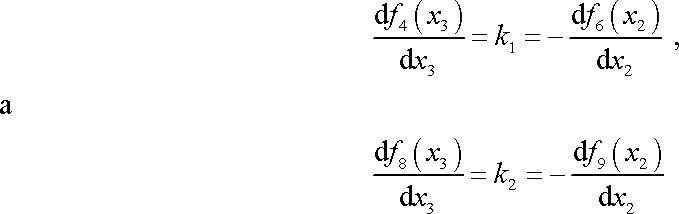 , , |
(3,116) |
odkud
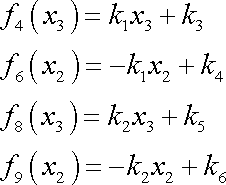 . . |
(3,117) |
Symboly
 značí konstanty.
značí konstanty.
Porovnáme vyjádření funkce
 rovnicemi
(3,110)
a
(3,113)
, do kterých
dosadíme dle
(3,117)
. Dostaneme
rovnicemi
(3,110)
a
(3,113)
, do kterých
dosadíme dle
(3,117)
. Dostaneme
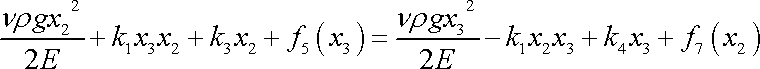 . . |
(3,118) |
Poslední rovnici lze splnit, když položíme
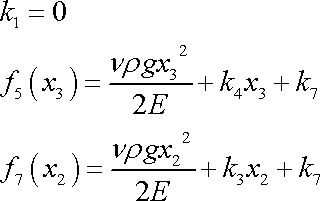 . . |
(3,119) |
Tak získáme pro
 vyjádření
vyjádření
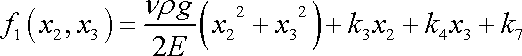 . . |
Dosadíme-li do
(3,114)
z
(3,117)
a položíme-li dle
(3,119)
 ,
dostaneme
,
dostaneme
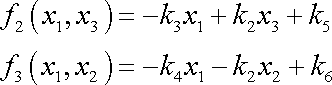 . . |
Po dosazení posledních výrazů do
(3,107)
dostáváme vektor posunutí
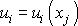 ;
;
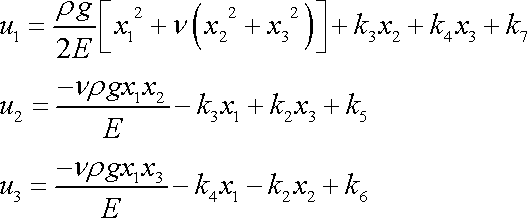 . . |
(3,120) |
Konstanty
 podobně jako v případě tahu (čl. 3.3)
charakterizují otočení válce jako celku, a proto je položíme rovny nule. Dle
zadání úlohy (viz též obr.56) předpokládáme
podobně jako v případě tahu (čl. 3.3)
charakterizují otočení válce jako celku, a proto je položíme rovny nule. Dle
zadání úlohy (viz též obr.56) předpokládáme
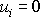 pro bod
pro bod
 .
Z této podmínky plyne
.
Z této podmínky plyne
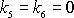 a
a
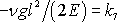 ,
uvážíme-li, že jsme již položili
,
uvážíme-li, že jsme již položili
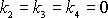 .
.
Konečné vyjádření pro vektor posunutí zde uvažovaného válce namáhaného vlastní tíhou je
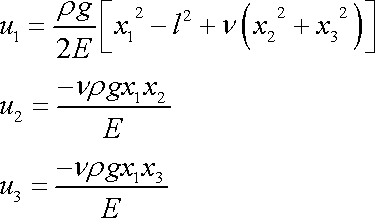 . . |
(3,121) |
První z rovnic
(3,121)
ukazuje, že bod na ose
válce
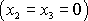 klesne o úsek délky
klesne o úsek délky
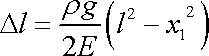 . . |
(3,122) |
Rovinný průřez kolmý k ose válce se stane rotačním paraboloidem, jehož body vzdálené od osy leží výše, než vrchol paraboloidu ležící na ose válce. Z druhých dvou rovnic plyne, že posunutí ve směru radiálním
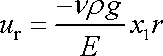 |
(3,123) |
 směřuje k ose válce s výjimkou bodů
ve spodní podstavě, kde je nulové.
směřuje k ose válce s výjimkou bodů
ve spodní podstavě, kde je nulové.
Válec se ve své vrchní části zúží. Z rovnice
(3,123)
plyne, že přímky rovnoběžné s osou (
 ) zůstanou přímkami i po deformaci,
neboť
) zůstanou přímkami i po deformaci,
neboť
 je přímo úměrné souřadnici
je přímo úměrné souřadnici
 .
Na obr.57 je osovým řezem znázorněn tvar, který válec zaujme po deformaci. Jeho
tvar před deformací je znázorněn čárkovaně. Nevyšetřujeme-li podrobně poměry
v příčných průřezech tyče (např. u drátů) a zajímá-li nás pouze její osové
prodloužení vlastní tíhou, můžeme k výrazu
(3,122)
, který pro
.
Na obr.57 je osovým řezem znázorněn tvar, který válec zaujme po deformaci. Jeho
tvar před deformací je znázorněn čárkovaně. Nevyšetřujeme-li podrobně poměry
v příčných průřezech tyče (např. u drátů) a zajímá-li nás pouze její osové
prodloužení vlastní tíhou, můžeme k výrazu
(3,122)
, který pro
 dává celkové prodloužení tyče
dává celkové prodloužení tyče
 ,
dojít jednodušší úvahou, jak je ukázáno např. v [8], kap. 8, příklad 4.
,
dojít jednodušší úvahou, jak je ukázáno např. v [8], kap. 8, příklad 4.
V této kapitole jsme uvedli řešení několika jednoduchých úloh teorie pružnosti. Další úkoly, jakými jsou např. obecné řešení rovinného problému, vyšetřování deformací membrán a skořepin, složitější problémy ohybu a torze tyčí, řešení některých speciálních případů trojrozměrné deformace, napětí vzbuzené rozdíly teplot, kmity strun, membrán a tyčí, otázky šíření deformačních vln v hmotném prostředí, jsou řešeny v [1], [10], [11], [12], [13], [14], [17], [18].
[*] Pro torzní tuhost se dříve užívalo označení direkční moment.
[+]Pro
výraz
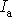 se užívalo označení plošný moment nebo i
plošný moment setrvačnosti. Užívání názvů moment setrvačnosti pro
charakteristiky různých ploch bylo v pružnosti běžné. Není však vhodné,
protože rozměr těchto veličin je různý od rozměru momentu setrvačnosti. Např.
veličina
se užívalo označení plošný moment nebo i
plošný moment setrvačnosti. Užívání názvů moment setrvačnosti pro
charakteristiky různých ploch bylo v pružnosti běžné. Není však vhodné,
protože rozměr těchto veličin je různý od rozměru momentu setrvačnosti. Např.
veličina
 má rozměr
m4, zatímco moment
setrvačnosti má rozměr kg.m2.
Užívání výše uvedených současnou normou zavedených názvů pro veličinu
má rozměr
m4, zatímco moment
setrvačnosti má rozměr kg.m2.
Užívání výše uvedených současnou normou zavedených názvů pro veličinu
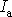 je tedy velmi žádané.
je tedy velmi žádané.