Vyjdeme-li při popisu smyku z vektoru posunutí
 ,
je smyk v rovině kolmé k třetí ose souřadnic zadán rovnicemi
,
je smyk v rovině kolmé k třetí ose souřadnic zadán rovnicemi
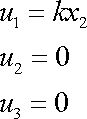 . . |
(3,55) |
Na obr.45 je znázorněno posunutí
řezu kvádru kolmého k ose
 odpovídající rovnicím
(3,55)
. Obdélníkový
průřez se deformuje na rovnoběžník. Pro jeden bod původně ležící v rovině
procházející počátkem a kolmé k ose
odpovídající rovnicím
(3,55)
. Obdélníkový
průřez se deformuje na rovnoběžník. Pro jeden bod původně ležící v rovině
procházející počátkem a kolmé k ose
 je na obrázku vyznačen vektor posunutí
je na obrázku vyznačen vektor posunutí
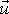 .
Z první rovnice
(3,55)
plyne pro úhel smyku
.
Z první rovnice
(3,55)
plyne pro úhel smyku
 vyjádření
vyjádření
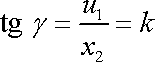 . . |
(3,56) |
Smyk ve stejné rovině je možno popsat i vektorem posunutí
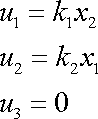 . . |
(3,57) |
 Posunutí řezu kvádru dané rovnicemi
(3,57)
je
znázorněno na obr.46. Pro úhly
Posunutí řezu kvádru dané rovnicemi
(3,57)
je
znázorněno na obr.46. Pro úhly
 platí vyjádření
platí vyjádření
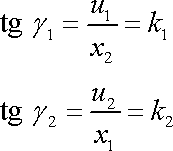 . . |
(3,58) |
Vypočteme dle (1,31) složky tenzoru deformace odpovídající vektorům posunutí (3,55) , dostáváme
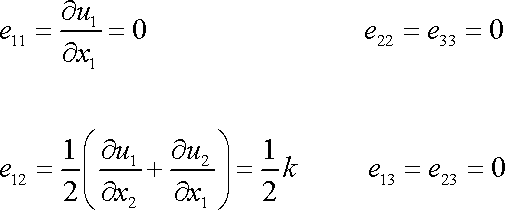 . . |
(3,59) |
Podobně pro vektory (3,57)
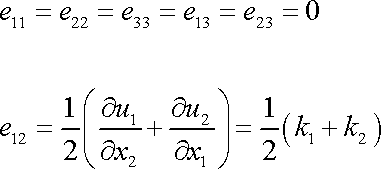 . . |
(3,60) |
Oběma způsobům zápisu vektoru posunutí odpovídá tedy stejný
typ tenzoru deformace (
 ,
ostatní
,
ostatní
 ). Z hlediska deformace jsou oba druhy
smyku ekvivalentní. Položíme-li
). Z hlediska deformace jsou oba druhy
smyku ekvivalentní. Položíme-li
 ,
je vzhledem ke stálému předpokladu malých deformací
,
je vzhledem ke stálému předpokladu malých deformací
 .
Potom i úhel smyku je v obou případech stejný.
.
Potom i úhel smyku je v obou případech stejný.
Sledujeme-li přímo posunutí, liší se smyk popsaný rovnicemi (3,55) (obr.45) od smyku popsaného rovnicemi (3,57) (obr.43) různým otočením vzorku. Při posunutí naznačeném na obrázku 45 dochází k otočení vzorku o úhel, který je dán výrazem (viz úvahy kolem rovnice (1,16) )
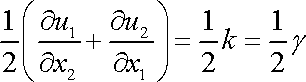 . . |
(3,61) |
Při posunutí znázorněném na obr.46, zvolíme-li
v rovnicích
(3,57)
 ,
k otočení vzorku nedochází;
,
k otočení vzorku nedochází;
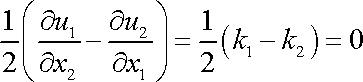 . . |
(3,62) |
Z hlediska posunutí se někdy oba druhy smyku rozlišují.
Smyk odpovídající obr.46, je-li
 a tedy též
a tedy též
 ,
se nazývá čistý smyk, smyk
z obr.45 se nazývá prostý smyk.
Rozlišení je nutné, uvažujeme-li velké deformace (srov. teorie velkých
deformací - str. 51).
,
se nazývá čistý smyk, smyk
z obr.45 se nazývá prostý smyk.
Rozlišení je nutné, uvažujeme-li velké deformace (srov. teorie velkých
deformací - str. 51).
V klasické teorii pružnosti, kde uvažujeme pouze malé deformace, není třeba oba druhy smyku rozlišovat. Pro další rozbor smyku vyjdeme z tenzoru malých deformací, který pro smyk má složky
 . . |
(3,63) |
V posledním vyjádření
 je úhel smyku. Vzhledem k tomu, že
deformace jsou dle předpokladu malé, je rovnost
je úhel smyku. Vzhledem k tomu, že
deformace jsou dle předpokladu malé, je rovnost
 polovičnímu úhlu smyku přesnou rovnicí.[*]
Deformaci
(3,6)
odpovídá dle Hookova zákona
(2,8)
napětí
polovičnímu úhlu smyku přesnou rovnicí.[*]
Deformaci
(3,6)
odpovídá dle Hookova zákona
(2,8)
napětí
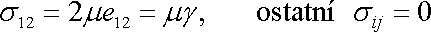 . . |
(3,64) |
 Napětí dané v každém bodě tělesa
rovnicemi
(3,64)
splňuje podmínky rovnováhy
(3,8)
, když zanedbáme objemové
síly
Napětí dané v každém bodě tělesa
rovnicemi
(3,64)
splňuje podmínky rovnováhy
(3,8)
, když zanedbáme objemové
síly
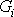 .
Za smykově namáhané těleso budeme pokládat kvádr z obr.45 nebo obr.46 a
vyšetříme okrajové podmínky
(3,14)
na jeho povrchu. Při formulaci okrajových
podmínek budeme vycházet z nedeformovaného
stavu tělesa, jak je obvyklé v klasické teorii pružnosti. Na obr.47 jsou
znázorněny normály na plochách kvádru kolmých k souřadnicovým osám. Vektor
normály
.
Za smykově namáhané těleso budeme pokládat kvádr z obr.45 nebo obr.46 a
vyšetříme okrajové podmínky
(3,14)
na jeho povrchu. Při formulaci okrajových
podmínek budeme vycházet z nedeformovaného
stavu tělesa, jak je obvyklé v klasické teorii pružnosti. Na obr.47 jsou
znázorněny normály na plochách kvádru kolmých k souřadnicovým osám. Vektor
normály
 na ploše kolmé k první ose,
orientujeme-li jej ve směru rostoucích hodnot
na ploše kolmé k první ose,
orientujeme-li jej ve směru rostoucích hodnot
 ,
má složky
,
má složky
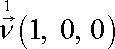 . . |
Podobně složky normál
 ,
na plochách kolmých k druhé a třetí souřadnicové ose při stejné orientaci
jsou
,
na plochách kolmých k druhé a třetí souřadnicové ose při stejné orientaci
jsou
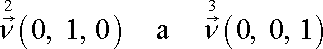 . . |
Rovnice
(3,14)
pro hraniční plochu kvádru kolmou
k první ose, jejíž vnější normála je
 ,
určuje složky vektoru napětí
,
určuje složky vektoru napětí
 ,
který musí na plochu při smyku
z vnějšku působit;
,
který musí na plochu při smyku
z vnějšku působit;
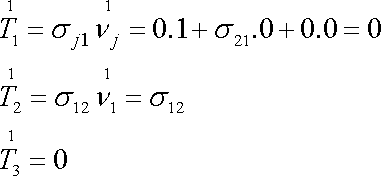 . . |
Okrajové podmínky na protilehlé stěně kvádru (tato plocha má
vnější normálu
 a prochází počátkem souřadnicové soustavy
znázorněné na obr.47 a 48 ) dávají
a prochází počátkem souřadnicové soustavy
znázorněné na obr.47 a 48 ) dávají
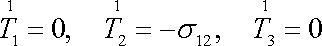 . . |
Na plochách kolmých k druhé souřadnicové ose dostáváme
*) Nejběžnější označení m by se pletlo s Laméovým koeficientem, záměna druhého normou doporučeného označení n se stejně označeným jednotkovým vektorem je méně pravděpodobná.
[*]V teorii
malých deformací, tedy v klasické teorii pružnosti, je rovnost úhlu
smyku
 dvojnásobné hodnotě smykové složky
dvojnásobné hodnotě smykové složky
 tenzoru malých deformací přesnou rovnicí a
vyjádření
(3,56)
, kde úhel
tenzoru malých deformací přesnou rovnicí a
vyjádření
(3,56)
, kde úhel
 je nahrazen
je nahrazen
 rovnicí přibližnou. Platí tedy
rovnicí přibližnou. Platí tedy
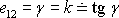 .
V teorii malých deformací však i přibližná rovnost
.
V teorii malých deformací však i přibližná rovnost
 hodnotě
hodnotě
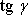 je vždy dostatečně přesně splněna. Při
přechodu k velkým deformacím je však již nutno mezi
je vždy dostatečně přesně splněna. Při
přechodu k velkým deformacím je však již nutno mezi
 a
a
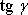 přesně rozlišovat a při nahrazení tenzoru
malých deformací tenzorem velkých deformací již žádné výše uvažované aproximace
nejsou platné.
přesně rozlišovat a při nahrazení tenzoru
malých deformací tenzorem velkých deformací již žádné výše uvažované aproximace
nejsou platné.
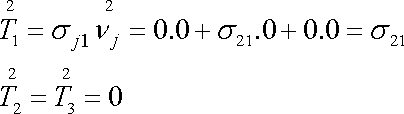 |
pro plochu s vnější normálou
 a
a
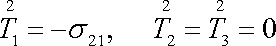 |
pro plochu s vnější normálou
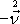 .
.
 Obdobně lze vypočítat, že na plochách kolmých
k třetí ose souřadnic je vektor napětí
Obdobně lze vypočítat, že na plochách kolmých
k třetí ose souřadnic je vektor napětí
 nulový. Vektory
nulový. Vektory
 působící při smyku na kvádr jsou naznačeny
na obr.48.
působící při smyku na kvádr jsou naznačeny
na obr.48.
Působíme-li na vrchní podstavu kvádru silou
 a na spodní silou
a na spodní silou
 ,
jak je naznačeno na obr.8 (na str. 27), bude, uvážíme-li tvrzení
Saint-Venantova principu (konec čl.3.2), smykové napětí
,
jak je naznačeno na obr.8 (na str. 27), bude, uvážíme-li tvrzení
Saint-Venantova principu (konec čl.3.2), smykové napětí
 .
Zvolíme-li v obr.8 soustavu souřadnic tak, že druhá osa je kolmá
k podstavám, na něž působí síly
.
Zvolíme-li v obr.8 soustavu souřadnic tak, že druhá osa je kolmá
k podstavám, na něž působí síly
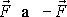 a první osa má směr působící síly
a první osa má směr působící síly
 ,
dostáváme případ, který jsme právě vyšetřovali. Smykové napětí je rovno
složce
,
dostáváme případ, který jsme právě vyšetřovali. Smykové napětí je rovno
složce
 tenzoru napětí;
tenzoru napětí;
 .
Výpočtem jsme ukázali, že k vytvoření smyku, je kromě sil
.
Výpočtem jsme ukázali, že k vytvoření smyku, je kromě sil
 působících na plochy kolmé k druhé
souřadnicové ose nutně působit i silami, které vytváří stejně velké smykové
napětí
působících na plochy kolmé k druhé
souřadnicové ose nutně působit i silami, které vytváří stejně velké smykové
napětí
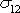 i na plochách kolmých k první souřadnicové
ose (viz obr.48).
i na plochách kolmých k první souřadnicové
ose (viz obr.48).
Při výkladu k obr.8 jsme uváděli, že tyto síly přenese
na vzorek uložení U zabraňující převrácení vzorku jako celku.
Nyní vidíme, že toto uložení musí být takové, aby dle Saint-Venantova principu
realizovalo ve vzorku na plochách kolmých k druhé souřadnicové ose
v nepříliš velké vzdálenosti od upevnění rovnoměrně rozložené smykové
napětí o velikosti
 .
.
V souvislosti s odkazem na obr.8 vyjadřujeme
smykové napětí jako
 .
Dosadíme-li toto vyjádření do rovnice
(3,64)
, dostáváme znovu elementární
Hookův zákon pro smyk
.
Dosadíme-li toto vyjádření do rovnice
(3,64)
, dostáváme znovu elementární
Hookův zákon pro smyk
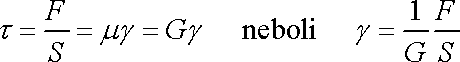 , , |
(2,40) |
který jsme pod stejným číslem (2,40) uvedli již v čl. 2.1.
Torzí rozumíme deformaci tyče (obecného válce), při níž
dochází k vzájemnému stáčení průřezů kolmých k podélné ose tyče.
Rozebereme podrobněji torzi tyče kruhového průřezu neboli torzi válce
s kruhovou podstavou (obr.49). Mírou torze je úhel
 ,
o který se vůči sobě pootočí dva průřezy vzdálené od sebe o jednotkovou délku.
Je-li délka válce l, je úhel
,
o který se vůči sobě pootočí dva průřezy vzdálené od sebe o jednotkovou délku.
Je-li délka válce l, je úhel
 stočení vrchní podstavy oproti spodní
podstavě dán výrazem
stočení vrchní podstavy oproti spodní
podstavě dán výrazem
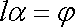 . . |
(3,65) |

Každý element vzorku je posunut (translace), otočen a deformován. Na obr.49 je
znázorněn jeden takový element. Jeho postavení před torzí je označeno K´, po torzi K. Neuvažujeme-li posunutí a otočení kolem třetí osy, prodělá
každý element válce prostý smyk znázorněný na obr.50. Výška na obr.50 znázorněného
elementu je
 .
Pootočení roviny, v které se nachází vrchní podstava elementu, proti
rovině spodní podstavy je tedy
.
Pootočení roviny, v které se nachází vrchní podstava elementu, proti
rovině spodní podstavy je tedy
 .
Pro element vzdálený r
od osy válce lze posunutí du
vrchní podstavy oproti spodní vyjádřit jako
.
Pro element vzdálený r
od osy válce lze posunutí du
vrchní podstavy oproti spodní vyjádřit jako
 .
Pro úhel smyku
.
Pro úhel smyku
 v uvažovaném přiblížení, kdy
v uvažovaném přiblížení, kdy
 pokládáme roven
pokládáme roven
 ,
dostáváme
,
dostáváme
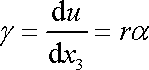 . . |
(3,66) |
Z elementárního Hookova zákona
(2,40)
pak pro smykové
napětí
 působící na podstavách elementu kolmých
k ose válce plyne
působící na podstavách elementu kolmých
k ose válce plyne
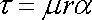 . . |
(3,67) |
V souřadnicové soustavě zvolené na obr.49 je osa válce
třetí souřadnicovou osou a smykové napětí na plochách kolmých k této ose
je tvořeno složkami
 tenzoru napětí, tedy
tenzoru napětí, tedy
 .
Rovina smyku všech elementů je kolmá k poloměru r, proto i smykové
napětí
(3,67)
je kolmé k poloměru. Skalární součin jeho složek
.
Rovina smyku všech elementů je kolmá k poloměru r, proto i smykové
napětí
(3,67)
je kolmé k poloměru. Skalární součin jeho složek
 s vektorem o složkách
s vektorem o složkách
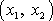 ,
který míří ve směru poloměru, musí být nulový. Z podmínek
,
který míří ve směru poloměru, musí být nulový. Z podmínek
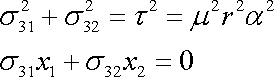 |
(3,68) |
dostáváme pro složky
 vyjádření
vyjádření
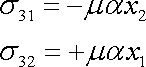 . . |
(3,69) |
Podmínkám
(3,68)
vyhovuje i řešení
 a
a
 odpovídající opačnému smyslu torze. Toto
řešení však z hlediska deformace není třeba odlišovat od řešení
(3,69)
,
a proto dále budeme rozebírat jen řešení
(3,69)
.
odpovídající opačnému smyslu torze. Toto
řešení však z hlediska deformace není třeba odlišovat od řešení
(3,69)
,
a proto dále budeme rozebírat jen řešení
(3,69)
.
Při torzi nepředpokládáme působení jiných než právě uvažovaných smykových napětí, proto položíme všechny ostatní složky tenzoru napětí rovny nule. Tenzor napětí při torzi kruhového přímého válce má složky
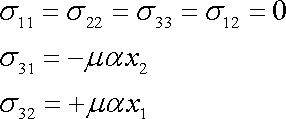 . . |
(3,70) |
Z rovnice (3,70) užitím Hookova zákona (2,8) dostáváme pro složky tenzoru deformace
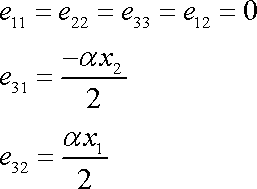 . . |
(3,71) |
Zanedbáme-li působení objemových sil, vyhovuje napětí (3,70) podmínkám rovnováhy, jak se lze přesvědčit dosazením jeho složek do rovnic (3,8) . Napětí na plášti válce při torzi má být nulové. Okrajové podmínky (3,14) pro plášť válce po dosazení složek napětí (3,70) dávají
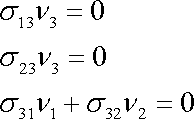 . . |
(3,72) |
Normála k plášti válce má nulovou třetí složku
 ,
a proto první dvě rovnice jsou triviálně splněny. Pro splnění třetí rovnice je
nutno uvážit, že normála
,
a proto první dvě rovnice jsou triviálně splněny. Pro splnění třetí rovnice je
nutno uvážit, že normála
 na válcové ploše má směr poloměru;
na válcové ploše má směr poloměru;
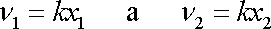 , , |
(3,73) |
kde k
je konstanta volená tak, aby normála
 měla jednotkovou velikost. Dosadíme-li
z
(3,70)
a
(3,73)
do poslední rovnice
(3,72)
, dostáváme
měla jednotkovou velikost. Dosadíme-li
z
(3,70)
a
(3,73)
do poslední rovnice
(3,72)
, dostáváme
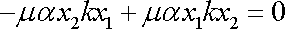 , , |
což je zřejmě splněno.
Nemá-li tyč podrobená torzi kruhový průřez, rovnice (3,73) neplatí a splnění třetí podmínky (3,72) na plášti válce působí obtíže. Ukazuje se, že pro splnění podmínek torze v případě tyče nekruhového průřezu je třeba uvažovat i posunutí ve směru podélné osy tyče. Průřezy kolmé k ose tyče přestávají po torzi být rovinnými (řešení viz např. [1], čl. 7.4, [17] ).
Na vrchní i spodní podstavě kruhového válce budou okrajové
podmínky
(3,14)
splněny, když vektor napětí
 bude v každém bodě podstavy roven
z vnějšku působícímu napětí. Přesně by to znamenalo, uvážíme-li zadání
tenzoru napětí rovnicemi
(3,70)
, vytvořit na obou podstavách vnější smykové
napětí působící ve směru kolmém k poloměrům kruhových podstav, při čemž
velikost smykových napětí by dle
(3,67)
vzrůstala se vzdáleností od středu
kruhu. Na obr.51 jsou směr a velikost takových smykových napětí
bude v každém bodě podstavy roven
z vnějšku působícímu napětí. Přesně by to znamenalo, uvážíme-li zadání
tenzoru napětí rovnicemi
(3,70)
, vytvořit na obou podstavách vnější smykové
napětí působící ve směru kolmém k poloměrům kruhových podstav, při čemž
velikost smykových napětí by dle
(3,67)
vzrůstala se vzdáleností od středu
kruhu. Na obr.51 jsou směr a velikost takových smykových napětí
 znázorněny vektorovými šipkami. Vzhledem k
opačnému smyslu normál na obou podstavách, bude na nich i rozdílný smysl, ve
kterém se smykové napětí snaží podstavou otočit.
znázorněny vektorovými šipkami. Vzhledem k
opačnému smyslu normál na obou podstavách, bude na nich i rozdílný smysl, ve
kterém se smykové napětí snaží podstavou otočit.
 Při konkrétní realizaci torze nemusíme
vytvořit na podstavách rozložení napětí přesně odpovídající obr.51. Takové
rozložení se dle Saint-Venantova principu ustaví v dostatečné vzdálenosti
od konců válce, i když torzní napětí na konci válce vytvoříme jiným způsobem.
Musíme však zachovat výsledné silové působení, v daném případě musíme
zachovat velikost M výsledného momentu sil.
Tuto velikost vypočteme.
Při konkrétní realizaci torze nemusíme
vytvořit na podstavách rozložení napětí přesně odpovídající obr.51. Takové
rozložení se dle Saint-Venantova principu ustaví v dostatečné vzdálenosti
od konců válce, i když torzní napětí na konci válce vytvoříme jiným způsobem.
Musíme však zachovat výsledné silové působení, v daném případě musíme
zachovat velikost M výsledného momentu sil.
Tuto velikost vypočteme.
Smykové napětí
 je kolmé k poloměru (viz obr.51).
Elementární příspěvek dM
k výslednému momentu sil M
je pak dán přímo součinem elementu síly
je kolmé k poloměru (viz obr.51).
Elementární příspěvek dM
k výslednému momentu sil M
je pak dán přímo součinem elementu síly
 a vzdálenosti r jejího působiště od osy válce;
a vzdálenosti r jejího působiště od osy válce;
 .
Velikost M výsledného momentu sil
působících při torzi na podstavu válce je tedy
.
Velikost M výsledného momentu sil
působících při torzi na podstavu válce je tedy
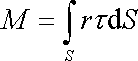 . . |
(3,74) |
Dosadíme-li do
(3,74)
velikost
 danou rovnicí
(3,67)
a provedeme-li výpočet
plošného integrálu přes kruhovou plochu poloměru R podstavy válce, dostaneme postupně
danou rovnicí
(3,67)
a provedeme-li výpočet
plošného integrálu přes kruhovou plochu poloměru R podstavy válce, dostaneme postupně
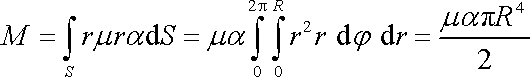 . . |
(3,75) |
Dosadíme za
 dle
(3,65)
a místo
dle
(3,65)
a místo
 napíšeme běžněji užívané označení G modulu pružnosti ve smyku. Získáme důležitý
vzorec
napíšeme běžněji užívané označení G modulu pružnosti ve smyku. Získáme důležitý
vzorec
Pro danou tyč je moment síly M úměrný úhlu stočení
 .
.
Úměrnost mezi úhlem stočení a momentem síly platí i pro torzi tyčí složitějších průřezů. Píšeme
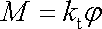 |
(3,76´) |
a konstantu úměrnosti
 nazýváme torzní tuhost[*].
Tyč kruhového průřezu má torzní tuhost
nazýváme torzní tuhost[*].
Tyč kruhového průřezu má torzní tuhost
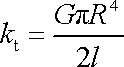 , , |
jak plyne z rovnice (3,76) .
Přestože řešení torze tyčí jiného než kruhového průřezu je
složitější i v rámci klasické teorie pružnosti, jak jsme se zmínili na
předcházející straně, rovnice
(3,76´)
je vhodnou první aproximací i pro ně.
Např. pro tyč obdélníkového průřezu s délkou stran b,
c
(
 .)lze
užít pro hodnotu
.)lze
užít pro hodnotu
 aproximační rovnici (např. [17] )
aproximační rovnici (např. [17] )
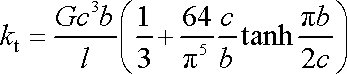 . . |
Upnutí vzorku tvaru kvádru je obvykle snazší než upnutí
vzorku kruhového průřezu. Proto je často výhodné pro měření modulu smyku G neznámých materiálů volit vzorky
s obdélníkovým průřezem a k výpočtu použít právě uvedený vzorec pro
torzní tuhost
 takových vzorků.
takových vzorků.
Odvození vztahu
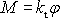 je provedeno v rámci klasické teorie
pružnosti. Dochází-li při torzi k velkým deformacím tyče, moment M přestává být úměrný úhlu
je provedeno v rámci klasické teorie
pružnosti. Dochází-li při torzi k velkým deformacím tyče, moment M přestává být úměrný úhlu
 .
Vztah
.
Vztah
 platí pro každou tyč jen do určité hodnoty
úhlu stočení
platí pro každou tyč jen do určité hodnoty
úhlu stočení
 .
Pro dlouhé kruhové tyče malého poloměru je však úměrnost dobře splněna do
značných hodnot úhlu
.
Pro dlouhé kruhové tyče malého poloměru je však úměrnost dobře splněna do
značných hodnot úhlu
 .
Úhel
.
Úhel
 je veličina, kterou lze měřit s velkou
přesností. Při malých průřezech a značných délkách tyče, které v tomto
případě nazýváme vlákny, direkční moment může být velmi malý. Rovnice
je veličina, kterou lze měřit s velkou
přesností. Při malých průřezech a značných délkách tyče, které v tomto
případě nazýváme vlákny, direkční moment může být velmi malý. Rovnice
 pak umožňuje citlivé měření momentů sil.
Torzně namáhaná vlákna se užívají v řadě citlivých měřících přístrojů,
např. v nejcitlivějších galvanometerech, v torzních vahách apod.
Kromě vláken kruhových průřezů (drátků) se často užívají i vlákna obdélníkových
průřezů (tenké pásky).
pak umožňuje citlivé měření momentů sil.
Torzně namáhaná vlákna se užívají v řadě citlivých měřících přístrojů,
např. v nejcitlivějších galvanometerech, v torzních vahách apod.
Kromě vláken kruhových průřezů (drátků) se často užívají i vlákna obdélníkových
průřezů (tenké pásky).
Veličiny
 při torzi válcové tyče jsou snadno měřitelné,
na základě rovnice
(3,76)
lze tedy stanovit modul smyku G materiálu, z kterého je tyč vyrobena
(viz [6], čl. 2.3.2 ). Jak jsme se zmínili výše, metoda není omezena na tyče kruhového průřezu a při známé torzní
tuhosti
při torzi válcové tyče jsou snadno měřitelné,
na základě rovnice
(3,76)
lze tedy stanovit modul smyku G materiálu, z kterého je tyč vyrobena
(viz [6], čl. 2.3.2 ). Jak jsme se zmínili výše, metoda není omezena na tyče kruhového průřezu a při známé torzní
tuhosti
 ji lze užít i na tyče jiného průřezu.
V knize [6] a
jejím druhém díle [7] lze nalézt popis řady přístrojů a různých měrných metod
užívajících torzně namáhaných vláken.
ji lze užít i na tyče jiného průřezu.
V knize [6] a
jejím druhém díle [7] lze nalézt popis řady přístrojů a různých měrných metod
užívajících torzně namáhaných vláken.