Tahem rozumíme namáhání vzorku znázorněné na obr.43b). Vyšetříme podrobně, jak vypadá
napětí, deformace a posunutí ve vzorku při tomto jednoduchém typu namáhání.
Souřadnicovou soustavu zvolíme způsobem naznačeným na obr.44. O vzorku
předpokládáme, že je kolmým válcem (tyčí) s obecným tvarem podstavy (kruh,
obdélník nebo i obecnější plocha). Počátek souřadnicové soustavy volíme
v jednom bodě vrchní podstavy. Předpokládáme, že na válcových plochách je
vnější napětí nulové a na podstavách válce působí vnější čisté tahové (případně
čisté tlakové) napětí, které má podél celé plochy konstantní velikost rovnou poměru F/S velikosti
F vnější síly a plochy S
průřezu válce. Příslušný napěťový vektor označíme
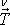 .
Vzhledem k volbě souřadnicové soustavy a dříve užívanému označování
vektorů napětí na plochách kolmých k souřad-nicovým osám, je
.
Vzhledem k volbě souřadnicové soustavy a dříve užívanému označování
vektorů napětí na plochách kolmých k souřad-nicovým osám, je
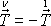 na vrchní podstavě a
na vrchní podstavě a
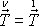 v bodech spodní podstavy válce.
v bodech spodní podstavy válce.
 Při vyšetřování tahu se zanedbává vliv
vlastní tíhy vzorku - vnější objemová síla
Při vyšetřování tahu se zanedbává vliv
vlastní tíhy vzorku - vnější objemová síla
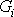 se pokládá za nulovou. Rovnice rovnováhy
(3,8)
lze pak splnit, pokládáme-li složky tenzoru
se pokládá za nulovou. Rovnice rovnováhy
(3,8)
lze pak splnit, pokládáme-li složky tenzoru
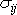 za konstantní v celém objemu vzorku
za konstantní v celém objemu vzorku
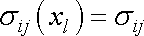 . . |
(3,15) |
Ve zvolené souřadnicové soustavě vektor
 na vrchní podstavě má složky
na vrchní podstavě má složky
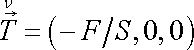 |
a na spodní podstavě je
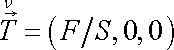 . . |
Okrajové podmínky
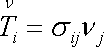 |
(3,14) |
pro vrchní podstavu, kde vektor vnější normály
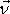 má složky
má složky
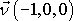 ,
dávají rovnice
,
dávají rovnice
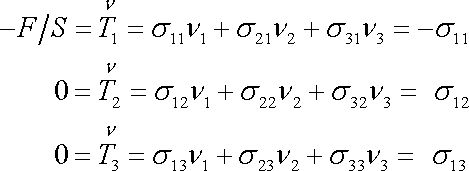 |
tedy
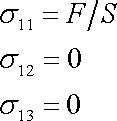 . . |
(3,16) |
Stejný výsledek plyne z podmínek
(3,14)
pro spodní
podstavu, kde vnější normála
 má složky
má složky
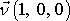 a
a
 složky
složky
 .
Na válcové ploše má vektor normály
.
Na válcové ploše má vektor normály
 nulovou složku
nulovou složku
 a nenulovou alespoň jednu ze složek
a nenulovou alespoň jednu ze složek
 .
Napěťový vektor
.
Napěťový vektor
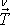 má na válcové ploše nulovou hodnotu. Rovnice
má na válcové ploše nulovou hodnotu. Rovnice
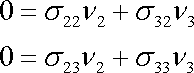 , , |
(3,17) |
které pro body válcové plochy plynou z podmínky (3,24) , ukazují, že nulovou hodnotu musí mít též složky tenzoru napětí
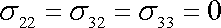 . . |
(3,18) |
Musíme totiž uvážit, že rovnice rovnováhy chceme splnit
konstantními hodnotami
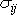 (viz
(3,15)
) v celém válci, a tedy i
na jeho povrchu. V rovnicích
(3,14)
(viz
(3,15)
) v celém válci, a tedy i
na jeho povrchu. V rovnicích
(3,14)
 mají
různé hodnoty v různých bodech válcové plochy, ale hodnoty
mají
různé hodnoty v různých bodech válcové plochy, ale hodnoty
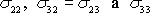 musí ve všech bodech být stejné. Potom
můžeme rovnice
(3,17)
splnit pouze, budou-li složky tenzoru napětí uvedené
v rovnicích
(3,18)
nulové.
musí ve všech bodech být stejné. Potom
můžeme rovnice
(3,17)
splnit pouze, budou-li složky tenzoru napětí uvedené
v rovnicích
(3,18)
nulové.
Položíme-li, jak ukazují rovnice (3,16) a (3,18) ,
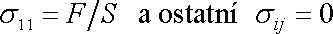 |
(3,19) |
v celém objemu válce, bude splněna jak rovnice rovnováhy (3,8) tak i okrajové podmínky (3,14) . Obraz napětí daný rovnicemi (3,19) bývá při tahovém napětí rovnou předpokládán. Zde jsme si ukázali, že takový obraz je ve shodě s obecnými podmínkami řešení úloh teorie pružnosti, které jsme uvedli v předcházejícím článku.
Zjistíme, jaké deformace odpovídají napětí danému rovnicemi (3,19) . Dosazením do Hookova zákona (2,8) dostáváme
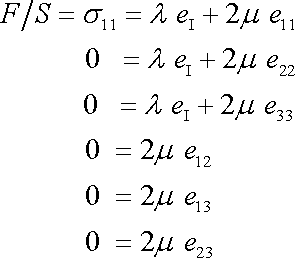 . . |
(3,20) |
Z posledních tří rovnic (3,20) plyne
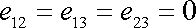 . . |
(3,21) |
Všechny smíšené složky tenzoru deformace jsou nulové. Pro uvažovanou deformaci jsou osy rovnoběžné s osami zvolené souřadnicové soustavy hlavními osami tenzoru deformace pro každý bod tělesa. Odečteme-li v systému (3,20) třetí rovnici od druhé, zjistíme, že
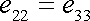 . . |
(3,22) |
Použijeme-li definiční rovnici
(1,104)
 prvního invariantu tenzoru a rovnici
(3,22)
,
dostáváme z druhé nebo třetí rovnice systému
(3,20)
vztah mezi složkami
prvního invariantu tenzoru a rovnici
(3,22)
,
dostáváme z druhé nebo třetí rovnice systému
(3,20)
vztah mezi složkami
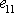 a
a
 tenzoru deformace;
tenzoru deformace;
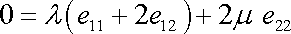 , , |
a tedy
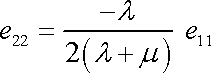 . . |
(3,23) |
Jak jsme ukázali v čl. 1.2 (rovnice
(1,58)
),
složky
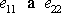 tenzoru deformace mají význam relativního
prodloužení ve směru první nebo druhé osy souřadnic. Je-li vzorek z obr.44
namáhán tahem, je
tenzoru deformace mají význam relativního
prodloužení ve směru první nebo druhé osy souřadnic. Je-li vzorek z obr.44
namáhán tahem, je
 kladné a dle
(3,23)
je pak ( l a m jsou kladné konstanty)
kladné a dle
(3,23)
je pak ( l a m jsou kladné konstanty)
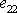 ,
a tedy též
,
a tedy též
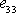 ,
záporné. Ve směru tahu nastává ve vzorku relativní prodloužení, ve směru kolmém
k tahu relativní zkrácení.
,
záporné. Ve směru tahu nastává ve vzorku relativní prodloužení, ve směru kolmém
k tahu relativní zkrácení.
Absolutní hodnota poměru relativního zkrácení k relativnímu prodloužení vzorku namáhaného tahem je další charakteristickou elastickou konstantou. Tato konstanta se nazývá Poissonův poměr nebo též Poissonovo číslo. Označíme ji n*) a z (3,23) pro ni dostaneme vyjádření
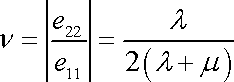 . . |
(3,24) |
Rovnice
(3,24)
doplňuje v čl. 2.1 uvažované vztahy mezi
charakteristickými elastickými koeficienty hookovské látky. V čl. 2.1
(rovnice
(2,14)
) jsme též ukázali, že invariant
 má význam relativní změny objemu vzorku. Pro
nestlačitelné materiály je
má význam relativní změny objemu vzorku. Pro
nestlačitelné materiály je
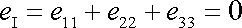 . . |
(3,25) |
Při tahovém namáhání je dle
(3,22)
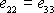 a z
(3,25)
dostáváme
a z
(3,25)
dostáváme
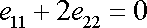 , , |
odkud
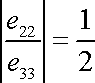 . . |
(3,26) |
Poissonův poměr n pro nestlačitelné materiály má hodnotu 1/2. U stlačitelných látek při tahovém namáhání dochází ke zvětšení objemu, potom
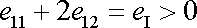 . . |
Jelikož
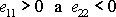 ,
musí platit
,
musí platit
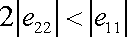 , , |
a tedy
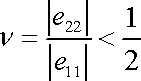 . . |
Pro běžné hookovské stlačitelné látky leží naměřená
hodnota
 v intervalu
v intervalu
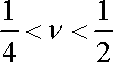 . . |
(3,27) |
Užijeme-li rovnic (3,22) a (3,23) , získáme pro první invariant tenzoru deformace vyjádření
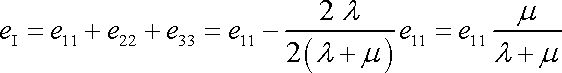 . . |
(3,28) |
Dosadíme-li tuto hodnotu za
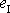 do první rovnice systému
(3,20)
, dostáváme
do první rovnice systému
(3,20)
, dostáváme
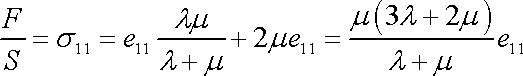 . . |
Rovnice
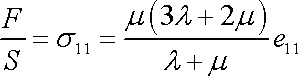 , , |
(3,29) |
kterou, vyjádříme-li relativní prodloužení
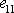 jako poměr přírůstku délky
jako poměr přírůstku délky
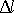 k původní délce l vzorku, můžeme psát v tvaru
k původní délce l vzorku, můžeme psát v tvaru
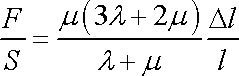 , , |
(3,30) |
je vyjádřením elementárního Hookova zákona pro tah. Porovnáme-li ze stření školy známý zápis tohoto zákona
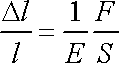 |
(3,31) |
s rovnicí
(3,30)
, vidíme, že konstanta
 je rovna modulu pružnosti v tahu neboli Youngovu modulu E;
je rovna modulu pružnosti v tahu neboli Youngovu modulu E;
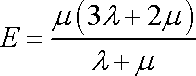 . . |
(3,32) |
Tak jsme získali vyjádření Youngova modulu dle Laméových koeficientů. Vztah (3,32) by bylo možno odvodit i porovnáním rovnic (2,8) a (2,9) . V článku 2.1 jsme však rovnici (2,9) uvedli, aniž bychom hledali její vztah k definiční rovnici (3,31) Youngova modulu E, a proto by tam provedené porovnání bylo ryze formální.
Vypočteme vektor posunutí
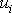 pro tah (3.16). Jak jsme ukázali, jsou při
tahu v souřadnicové soustavě zvolené na obr.44 nenulové složky
pro tah (3.16). Jak jsme ukázali, jsou při
tahu v souřadnicové soustavě zvolené na obr.44 nenulové složky
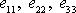 tenzoru deformace a složky se smíšenými
indexy
tenzoru deformace a složky se smíšenými
indexy
 jsou nulové. Rovnice
jsou nulové. Rovnice
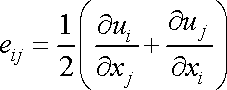 |
(1,31) |
mají v tomto případě tvar
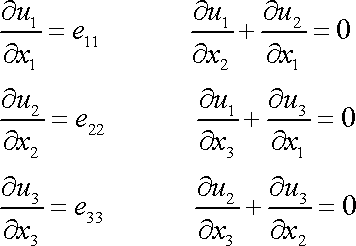 . . |
(3,33) |
Z rovnic na levé straně systému (3,33) plyne
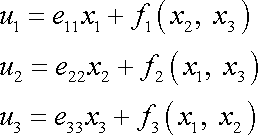 , , |
(3,34) |
kde
 jsou zatím neurčené funkce uvedených
nezávisle proměnných. Jejich tvar určíme z rovnic na pravé straně systému
(3,33)
. Dosadíme-li do prvé z nich funkce
jsou zatím neurčené funkce uvedených
nezávisle proměnných. Jejich tvar určíme z rovnic na pravé straně systému
(3,33)
. Dosadíme-li do prvé z nich funkce
 vyjádřené dle
(3,34)
, dostaneme
vyjádřené dle
(3,34)
, dostaneme
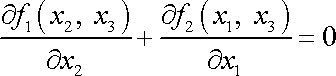 |
neboli
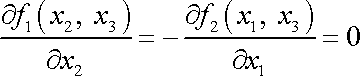 . . |
(3,35) |
Na levé straně rovnice
(3,35)
je funkce proměnných
 .
Označíme ji
.
Označíme ji
 .
Na pravé straně rovnice je funkce proměnných
.
Na pravé straně rovnice je funkce proměnných
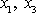 ,
kterou označíme
,
kterou označíme
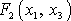 .
Má-li být splněna rovnost
(3,35)
, kterou nyní napíšeme jako
.
Má-li být splněna rovnost
(3,35)
, kterou nyní napíšeme jako
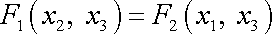 , , |
(3,35´) |
je nutné aby funkce
 byly závislé pouze na
byly závislé pouze na
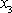 ,
tedy
,
tedy
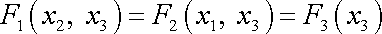 . . |
Pro funkce
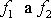 tak dostáváme podmínky
tak dostáváme podmínky
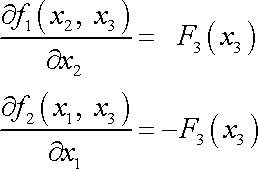 , , |
z kterých plyne
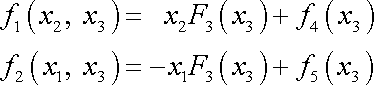 . . |
(3,36) |
Druhá rovnice na pravé straně systému (3,33) po dosazení z (3,34) dává vztah
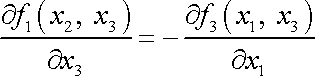 . . |
(3,37) |
Dosadíme-li do něj vyjádření
 dle
(3,36)
, dostáváme
dle
(3,36)
, dostáváme
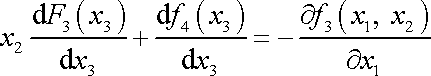 . . |
(3,38) |
Pravá strana poslední rovnice je funkcí pouze
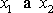 ,
a proto výrazy
,
a proto výrazy
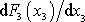 a
a
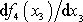 musí být konstantní;
musí být konstantní;
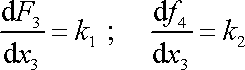 . . |
(3,39) |
Z posledních rovnic plyne
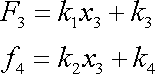 . . |
(3,40) |
Dosadíme-li do rovnice (3,38) vyjádření (3,39) , dostaneme
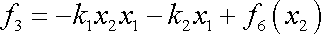 . . |
(3,41) |
Z poslední rovnice na pravé straně systému (3,33) plyne
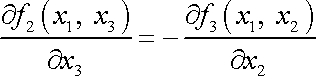 . . |
(3,42) |
Do rovnice
(3,42)
dosadíme vyjádření
 z
(3,41)
a
z
(3,41)
a
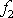 z
(3,36)
, přičemž
z
(3,36)
, přičemž
 vyjádříme dle
(3,40)
, dostaneme
vyjádříme dle
(3,40)
, dostaneme
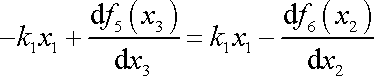 . . |
(3,43) |
Jednotliví sčítanci na obou stranách rovnice jsou funkcemi různých proměnných, ke splnění rovnice je tedy nutno položit
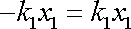 |
(3,44) |
a
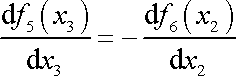 . . |
(3,45) |
První rovnici lze splnit, pouze když
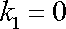 |
(3,46) |
a druhou, když funkce různých proměnných se budou rovnat
jedné a téže konstantě. Označíme-li tuto konstantu
 ,
můžeme psát
,
můžeme psát
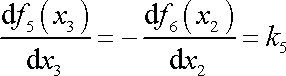 . . |
(3,47) |
Z poslední rovnice plyne
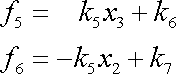 . . |
(3,48) |
Uvážíme-li rovnice
(3,36)
,
(3,40)
,
(3,41)
,
(3,46)
a
(3,48)
,
dostáváme pro funkce
 konečné vyjádření
konečné vyjádření
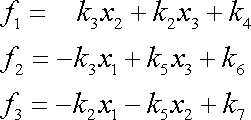 . . |
(3,49) |
Složky vektoru posunutí (3,34) mají tedy tvar
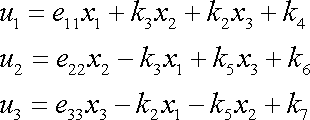 . . |
(3,50) |
Funkce
 jsou dány volbou bodu, pro který pokládáme
vektor posunutí
jsou dány volbou bodu, pro který pokládáme
vektor posunutí
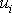 za nulový, a otočením tělesa jako celku.
Zvolíme-li za bod, pro který je vektor posunutí nulový, počátek souřadnicové
soustavy (viz obr.44) a předpokládáme-li, že k otočení nedochází, funkce
za nulový, a otočením tělesa jako celku.
Zvolíme-li za bod, pro který je vektor posunutí nulový, počátek souřadnicové
soustavy (viz obr.44) a předpokládáme-li, že k otočení nedochází, funkce
 budou mít nulovou hodnotu. Nulové posunutí
počátku souřadnicové soustavy je vystiženo rovnicemi
budou mít nulovou hodnotu. Nulové posunutí
počátku souřadnicové soustavy je vystiženo rovnicemi
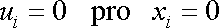 . . |
(3,51) |
Otočení nenastane, když posunutí bodů ležících na souřadnicových osách se bude dít pouze ve směru těchto os. Tuto podmínku lze zapsat takto
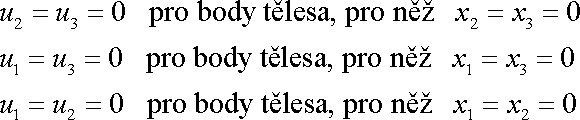 . . |
Dosadíme-li podmínky (3,51) a (3,52) do (3,50) , dostáváme
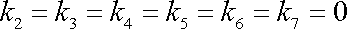 , , |
(3,53) |
a tedy
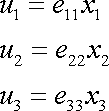 . . |
(3,54) |
Vyšetřujeme-li deformaci tělesa, jeho posunutí a otočení
jako celku není podstatné, a proto vyjádření vektoru
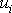 rovnicemi
(3,54)
můžeme pokládat za obecné
vyjádření vektoru posunutí pro vzorek namáhaný tahem, je-li soustava souřadnic
zvolena způsobem naznačeným na obr.44.
rovnicemi
(3,54)
můžeme pokládat za obecné
vyjádření vektoru posunutí pro vzorek namáhaný tahem, je-li soustava souřadnic
zvolena způsobem naznačeným na obr.44.