Základní úlohou teorie pružnosti je najít napětí a deformaci
v každém bodě tělesa, známe-li rozložení napětí nebo deformací na povrchu
tělesa. Přitom předpokládáme, že těleso je po deformaci v rovnováze. V
klasické teorii pružnosti (hookovská látka) lze tuto úlohu pro izotropní těleso
formulovat takto: máme najít pro každý bod tělesa složky tenzoru napětí
 a složky vektoru posunutí
a složky vektoru posunutí
 ,
které vyhovují rovnicím rovnováhy
,
které vyhovují rovnicím rovnováhy
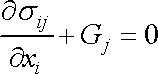 |
(3,8) |
a Hookovu zákonu
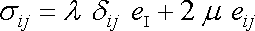 . . |
(2,8) |
Rovnice
(3,8)
a
(2,8)
reprezentují devět rovnic pro devět
neznámých funkcí
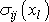 a
a
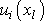 ,
uvážíme-li, že v rovnici
(2,8)
můžeme složky
,
uvážíme-li, že v rovnici
(2,8)
můžeme složky
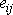 tenzoru deformace nahradit jejich vyjádřením
dle složek vektoru posunutí
tenzoru deformace nahradit jejich vyjádřením
dle složek vektoru posunutí
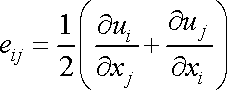 . . |
(1,31) |
Objemové síly
 jakožto vnější síly pokládáme za známé. Aby
úloha mohla být jednoznačně řešitelná, je nutno zadat hodnoty funkcí
jakožto vnější síly pokládáme za známé. Aby
úloha mohla být jednoznačně řešitelná, je nutno zadat hodnoty funkcí
 na okraji tělesa, neboli, jak se říká
v teorii parciálních diferenciálních rovnic ([9], kap. 18), je nutno zadat
okrajové podmínky. Jsou-li na povrchu tělesa dána posunutí
na okraji tělesa, neboli, jak se říká
v teorii parciálních diferenciálních rovnic ([9], kap. 18), je nutno zadat
okrajové podmínky. Jsou-li na povrchu tělesa dána posunutí
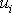 ,
jsou tím hned dány okrajové podmínky pro funkce
,
jsou tím hned dány okrajové podmínky pro funkce
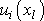 .
Dosazením do rovnic
(1,31)
získáme tenzor deformace
.
Dosazením do rovnic
(1,31)
získáme tenzor deformace
 pro body povrchu tělesa a dalším dosazením
do Hookova zákona
(2,8)
i hodnoty složek
pro body povrchu tělesa a dalším dosazením
do Hookova zákona
(2,8)
i hodnoty složek
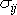 napětí v bodech povrchu tělesa, tedy
hledané funkce
napětí v bodech povrchu tělesa, tedy
hledané funkce
 .
.
Známe-li vektory napětí
 na povrchu tělesa, vychází se při stanovení
okrajových podmínek z rovnice
(1,82)
na povrchu tělesa, vychází se při stanovení
okrajových podmínek z rovnice
(1,82)
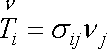 , , |
(3,14) |
která musí být splněna v bodech povrchu tělesa. Při řešení úloh klasické teorie pružnosti není třeba vzhledem k předpokladu o malých deformacích rozlišovat mezi deformovaným a nedeformovaným stavem tělesa. Tím se řešení úloh značně zjednoduší.
Rovnice
(3,8)
a
(2,8)
pokládáme za rovnice určující tenzor
napětí
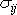 a vektor posunutí
a vektor posunutí
 .
Taková formulace umožňuje uvažovat o rovnicích
(3,8)
a
(2,8)
jako o devíti
rovnicích pro devět neznámých funkcí. Kdybychom rovnice
(3,8)
a
(2,8)
uvažovali
jako rovnice pro neznámé složky
.
Taková formulace umožňuje uvažovat o rovnicích
(3,8)
a
(2,8)
jako o devíti
rovnicích pro devět neznámých funkcí. Kdybychom rovnice
(3,8)
a
(2,8)
uvažovali
jako rovnice pro neznámé složky
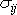 tenzoru napětí a
tenzoru napětí a
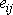 tenzoru deformace, měli bychom pouze devět
rovnic pro dvanáct neznámých funkcí. Rovnicemi
(1,31)
je šest funkcí
tenzoru deformace, měli bychom pouze devět
rovnic pro dvanáct neznámých funkcí. Rovnicemi
(1,31)
je šest funkcí
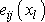 určeno na základě tří funkcí
určeno na základě tří funkcí
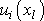 .
Mají-li funkce
.
Mají-li funkce
 popisovat deformaci spojitého tělesa, které
zůstane spojitým i po deformaci, nelze je volit libovolně, ale musí splňovat
jisté podmínky plynoucí z rovnice
(1,31)
. Těmto podmínkám se říká rovnice
kompatibility deformací (viz např. [1], čl. 4.3). Rovnice kompatibility je nutno připojit k rovnicím
(3,8)
a
(2,8)
, chceme-li je řešit přímo pro neznámé
popisovat deformaci spojitého tělesa, které
zůstane spojitým i po deformaci, nelze je volit libovolně, ale musí splňovat
jisté podmínky plynoucí z rovnice
(1,31)
. Těmto podmínkám se říká rovnice
kompatibility deformací (viz např. [1], čl. 4.3). Rovnice kompatibility je nutno připojit k rovnicím
(3,8)
a
(2,8)
, chceme-li je řešit přímo pro neznámé
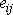 a
a
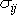 .
.
Udáním rovnic (3,8) , (2,8) (1,31) , (3,14) jsme naznačili, co je problémem teorie pružnosti. Při řešení jednotlivých úloh se základní formulace upravuje na tvary příhodnější ke konkrétním výpočtům. Jak se takové úpravy provádějí, způsoby řešení problémů, důkazy jednoznačnosti řešení apod., lze nalézt v [1] a v dalších učebnicích citovaných na začátku této kapitoly.
Pro řešení konkrétních úloh teorie pružnosti je velmi důležitý Saint-Venantův princip, který umožňuje zjednodušit při analytickém zadání skutečné okrajové podmínky úlohy. Dle tohoto principu stav napětí a deformace v místech tělesa dostatečně vzdálených od povrchu, na kterém působí vnější síly, je téměř stejný, nahradíme-li jedno rozložení sil jiným o stejné výsledné síle a stejném výsledném momentu sil.
 Např. při běžné tahové
zkoušce, kdy na vzorek V upevněný svorkami K působíme tahovými
silami
Např. při běžné tahové
zkoušce, kdy na vzorek V upevněný svorkami K působíme tahovými
silami
 (viz obr.43a) ), lze dle
Saint-Venantova principu zanedbat vliv svorek na způsob, jakým jsou síly
(viz obr.43a) ), lze dle
Saint-Venantova principu zanedbat vliv svorek na způsob, jakým jsou síly
 na vzorek přenášeny. Napětí ve vzorku V
v dos-tatečné vzdálenosti od jeho konců pokládáme za shodné s tím,
jaké by bylo způsobeno napěťovým vektorem
na vzorek přenášeny. Napětí ve vzorku V
v dos-tatečné vzdálenosti od jeho konců pokládáme za shodné s tím,
jaké by bylo způsobeno napěťovým vektorem
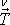 ,
jehož velikost by v obou čelních plochách vzorku byla konstantní a
rovna F/S. Symbolem S
je označena plocha průřezu vzorku. Směr a smysl vektoru
,
jehož velikost by v obou čelních plochách vzorku byla konstantní a
rovna F/S. Symbolem S
je označena plocha průřezu vzorku. Směr a smysl vektoru
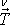 na každé z čelních ploch splývá se
skutečně působícími silami
na každé z čelních ploch splývá se
skutečně působícími silami
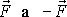 (viz obr.43b) ). Kdybychom
skutečné rozložení vnějších sil při tahové zkoušce, z které je pro vzorek
z hookovské látky odvozen elementární Hookův zákon pro tah
(viz obr.43b) ). Kdybychom
skutečné rozložení vnějších sil při tahové zkoušce, z které je pro vzorek
z hookovské látky odvozen elementární Hookův zákon pro tah
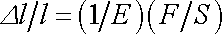 , , |
nemohli nahradit rozložením napěťových vektorů znázorněných na obr.43b), bylo by analytické zpracování i tohoto nejjednoduššího elastického pokusu značně obtížné.