
O kontinuu v rovnováze mluvíme tehdy, je-li v rovnováze každá jeho
část. Při odvozování rovnice rovnováhy vyjdeme z úvah týkajících se
konečného objemu kontinua jako při odvození rovnic
(1,82)
a
(1,87)
. Výhodné je
zvolit objem ve tvaru kvádru, jehož hrany o délkách a, b, c jsou rovnoběžné s osami souřadnic
(obr.42).
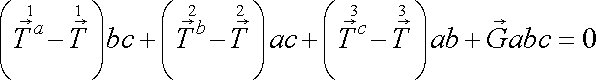 . . |
(3,1) |
V rovnici
(3,1)
stejně jako v článku 1.4
značíme
 vektor napětí působící na tu stranu plochy
kolmé k i-té ose souřadnic,
která je obrácena ke kladnému smyslu osy souřadnic. Postupujeme-li ve směru
rostoucích souřadnic
vektor napětí působící na tu stranu plochy
kolmé k i-té ose souřadnic,
která je obrácena ke kladnému smyslu osy souřadnic. Postupujeme-li ve směru
rostoucích souřadnic
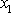 ,
napětí na první ploše kvádru kolmé k první ose souřadnic značíme
,
napětí na první ploše kvádru kolmé k první ose souřadnic značíme
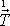 ,
napětí na druhé ploše kvádru kolmé k první ose značíme
,
napětí na druhé ploše kvádru kolmé k první ose značíme
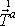 .
Obdobný je význam symbolů
.
Obdobný je význam symbolů
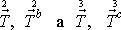 (viz obr.42). Plošné síly
(viz obr.42). Plošné síly
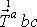 ,
,
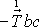 ,
,
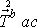 ,
,
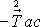 ,
,
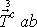 ,
,
 a objemová síla
a objemová síla
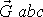 jsou všechny vnější síly působící na
uvažovaný kvádr, proto jejich součet klademe v
(3,1)
roven nule. Ve smyslu vět
o středních hodnotách diferenciálního počtu (např. [9], kap. 11),
pokládáme
jsou všechny vnější síly působící na
uvažovaný kvádr, proto jejich součet klademe v
(3,1)
roven nule. Ve smyslu vět
o středních hodnotách diferenciálního počtu (např. [9], kap. 11),
pokládáme
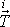 za vhodně volenou hodnotu napětí
v jednom bodě příslušné stěny kvádru a
za vhodně volenou hodnotu napětí
v jednom bodě příslušné stěny kvádru a
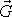 za hodnotu ve vhodně voleném bodu uvnitř
kvádru. Dle
(1,75)
složky vektorů
za hodnotu ve vhodně voleném bodu uvnitř
kvádru. Dle
(1,75)
složky vektorů
 jsou složkami
jsou složkami
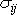 tenzoru napětí. První složku vektorové
rovnice
(3,1)
můžeme tedy zapsat v tvaru
tenzoru napětí. První složku vektorové
rovnice
(3,1)
můžeme tedy zapsat v tvaru
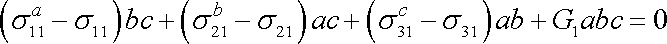 . . |
(3,2) |
Dle úvah užívaných ve větách o střední hodnotě lze rozdíly hodnot složek napětí na dvou protilehlých stěnách vyjádřit jako součin vzdálenosti obou ploch a derivace složky napětí dle souřadnice kolmé k uvažovaným plochám, přičemž hodnota derivace přísluší některému vnitřnímu bodu kvádru. Pro každou složku je to obecně jiný bod. Tedy
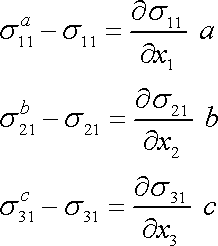 . . |
(3,3) |
S uvážením rovnice (3,3) přepíšeme rovnici (3,2) na tvar
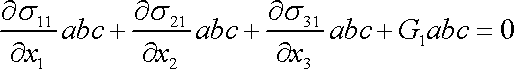 . . |
(3,4) |
Provádíme-li limitní zmenšování objemu kvádru, hodnotu
objemu abc můžeme v rovnici
(3,4)
vykrátit a hodnoty
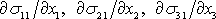 a
a
 ,
původně příslušné různým vnitřním bodům kvádru, v limitě přejdou na
hodnoty příslušné stejnému bodu, ke kterému limitním postupem kvádr stáhneme.
Pro tento bod pak platí rovnice
,
původně příslušné různým vnitřním bodům kvádru, v limitě přejdou na
hodnoty příslušné stejnému bodu, ke kterému limitním postupem kvádr stáhneme.
Pro tento bod pak platí rovnice
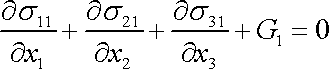 . . |
(3,5) |
Volba polohy kvádru v kontinuu i poloha bodu, ke kterému tento kvádr limitním postupem stáhneme, je libovolná, a proto rovnice (3,5) platí pro každý bod kontinua, které je v rovnováze.
Stejným postupem, jakým jsme z první složky vektorové rovnice (3,1) odvodili rovnici (3,5) , můžeme z druhé složky rovnice (3,2) odvodit rovnici
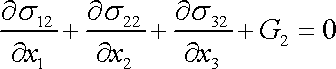 |
(3,6) |
a z třetí složky rovnice (3,1) rovnici
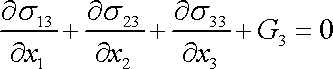 . . |
(3,7) |
Rovnice (3,5) , (3,6) , (3,7) tvoří hledanou rovnici rovnováhy kontinua, kterou s užitím složkové symboliky a sčítacího pravidla stručně zapíšeme jako
Odvození rovnice (3,8) užívající metod vektorové analýzy je uvedeno např. v [1], čl. 3.3.
Síly uvažované v rovnici (3,1) představují všechny vnější síly působící na kvádr, i když kontinuum není v rovnováze. Pro kvádr pak dle (I5,35) lze psát pohybovou rovnici
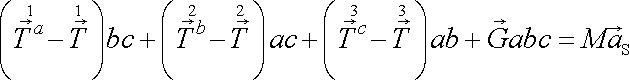 , , |
(3,9) |
v které M je hmotnost kvádru a
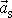 zrychlení hmotného středu kvádru.
Hmotnost M vyjádříme jako
zrychlení hmotného středu kvádru.
Hmotnost M vyjádříme jako
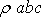 ,
kde
,
kde
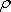 je hustota v některém vnitřním bodě
kvádru. Uvážíme-li smysl vektoru posunutí
je hustota v některém vnitřním bodě
kvádru. Uvážíme-li smysl vektoru posunutí
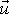 zavedeného rovnicí
(1,19)
, je zřejmé, že
zrychlení
zavedeného rovnicí
(1,19)
, je zřejmé, že
zrychlení
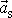 lze psát jako druhou derivaci dle času
lze psát jako druhou derivaci dle času
 vektoru posunutí hmotného středu, tj.
vnitřního bodu kvádru abc. Rovnici
(3,9)
můžeme pak přepsat na tvar
vektoru posunutí hmotného středu, tj.
vnitřního bodu kvádru abc. Rovnici
(3,9)
můžeme pak přepsat na tvar
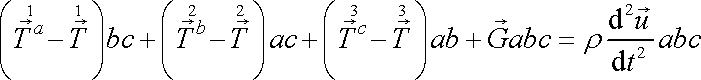 . . |
(3,10) |
Užijeme-li úpravy (3,4) levé strany rovnice (3,10) , dostaneme pro její první složku
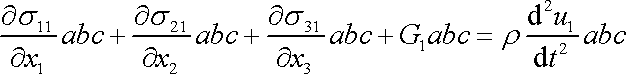 . . |
(3,11) |
Limitním zmenšováním kvádru získáme z (3,11) rovnici
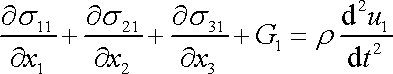 |
(3,12) |
platnou v každém bodě kontinua. Rovnice (3,12) spolu s rovnicemi
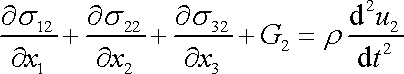 |
a
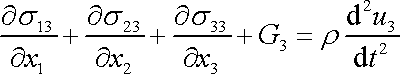 , , |
které plynou z druhých dvou složek rovnice (3,10) , tvoří pohybovou rovnici kontinua. Stručně pohybovou rovnici užitím složkové symboliky zapíšeme jako
Rovnice (3,13) je výchozí rovnicí dynamiky kontinua. Užívá se např. při vyšetřování pohybu tekutin (viz čl. 4.3) a při sledování vln šířících se kontinuem ([1], kap. 9).