V dosavadních úvahách o elektrostatickém poli jsme používali pojem elektrického náboje, respektive jeho hustoty. Předpokládali jsme, že náboj může být určitým způsobem rozložen v prostoru, toto rozložení jsme považovali za známé a nestarali jsme se o konkrétní fyzikální podmínky, za kterých k němu dochází. Byli jsme si přitom vědomi, že stabilní rozložení elektrických nábojů v prostoru není možno realizovat výhradně silami elektrostatického pole a že náboje musí být proto podrobeny i působení dalších sil, které jsme však blíže nespecifikovali.
Makroskopické náboje, které jsou dostupné našemu přímému pozorování a měření, jsou vždy ve skutečnosti vázány na své mikrofyzikální nositele, jako jsou elektrony, ionty apod. Chování těchto nábojů pak ovšem závisí na konkrétních fyzikálních podmínkách, jimž jsou tyto mikrofyzikální útvary vystaveny. Elektrony mohou být například vázány k atomovým jádrům jako součást elektronového obalu atomu, mohou vytvářet kvantový elektronový plyn ve vodičích, při teplotách blízkých absolutní nule mohou být ve formě tzv. Cooperových párů a generovat jev nazývaný supravodivostí, mohou vytvářet elektronový mrak nebo svazek letící ve vakuu a vyvolávat například luminiscenci televizní obrazovky nebo generovat elektromagnetické vlny. Otázkami tohoto druhu se budeme podrobněji zabývat v kapitole 7. Avšak chceme-li popsat reálné chování a účinky elektrických nábojů, musíme vzít některé tyto konkrétní fyzikální podmínky v úvahu i v elektrostatice.
Již v počátcích experimentálního studia elektrických jevů bylo známo, že různé látky mají různou schopnost být zelektrizovány a udrženy v tomto zelektrizovaném stavu. Například skleněnou nebo ebonitovou tyč je možno snadno zelektrizovat třením a udržet ji v tomto stavu, zatímco uzemněnou kovovou tyč tímto způsobem zelektrizovat nelze. Dále bylo zjištěno, že elektrický náboj lze dotykem přenášet z jednoho tělesa na druhé, přičemž různé látky se i v tomto směru chovají různě. Můžeme například zjistit, že skleněnou kouli lze vždy nabít dotykem s nabitými tělesy, zatímco kovovou kouli nabijeme tímto způsobem jen tehdy, leží-li na podložce z vhodného materiálu, například skla. Spojíme-li dvě osamocené kovové koule kovovou tyčí a nabijeme-li jednu z nich dotykem s nabitým tělesem, objeví se náboj ihned na druhé kouli. Provedeme-li stejný pokus s dvojicí kovových koulí spojených skleněnou tyčí, zjistíme, že náboj zůstal pouze na první kouli. Tedy zatímco kovová tyč převedla elektrický náboj z jedné koule na druhou, skleněná tyč toho schopna nebyla.
Látky, které jsou schopny převádět elektrický náboj, se nazývají elektrickými vodiči; látky, které tuto schopnost nemají, se nazývají nevodiči (dielektriky, izolanty). Všimněme si ještě podrobněji rozdílu mezi těmito dvěma druhy látek. Je-li zelektrizovaný vodič spojen vodivě se zemí (například tím, že jej držíme v ruce nebo že leží na kovovém stolku), odvádí se jeho náboj ihned do země a vodič se stále jeví neelektrickým. Chceme-li na vodiči náboj udržet, musí být ze všech stran obklopen nevodiči; jak říkáme, musí být izolován. Proto, jak jsme viděli, může být kovová koule nabita jen tehdy, leží-li na podložce z nevodivého materiálu. Dále, dotkneme-li se izolovaného vodiče na některém místě nabitým tělesem, stane se ihned nabitým po celém povrchu. Dotkneme-li se naopak nabitého izolovaného vodiče v kterémkoli místě vodičem spojeným se zemí, odvedeme ihned všechen náboj do země. Na druhé straně, jestliže se dotkneme tímto vodičem nabitého nevodivého tělesa, odvedeme do země jen náboj z místa dotyku.
Na základě uvedeného chování vodičů soudíme, že nositelé elektrických nábojů se mohou volně pohybovat v celém jejich objemu. Typickými představiteli vodičů jsou kovy, dále roztoky elektrolytů a ionizované plyny (plazma).
V kovech se mohou volně pohybovat některé elektrony (tzv. volné, vodivostní), ve vodivých kapalinách nebo plynech jsou pohyblivými nositely náboje atomární nebo molekulární ionty.
U nevodičů pak soudíme, že všichni nositelé náboje jsou v nich vázáni určitými silami, takže k přenosu náboje objemem nevodiče nemůže snadno docházet. Typickými představiteli nevodičů jsou sklo, slída, guma, většina umělých hmot (polymerů) apod. Kromě toho existují látky, které jsou podstatně hůře vodivé než jmenované vodiče, avšak podstatně lépe vodivé než jmenované nevodiče. Navíc jejich schopnost přenášet elektrický náboj je silně závislá na jejich chemické čistotě a vnějších podmínkách (teplotě, osvětlení, ozáření apod.). Tyto látky nazýváme polovodiči. Patří mezi ně některé prvky jako křemík, germanium, selen, dále krystaly GaAs, Cu2O, CdS, PbS a další.
V elektrostatice se zabýváme studiem fyzikálních projevů nepohybujících se elektrických nábojů. Nebudou nás proto příliš zajímat kvantitativní rozdíly v hodnotách vodivosti jednotlivých látek, poněvadž mohou pouze ovlivnit rychlost, s jakou bude dosaženo rovnovážného rozložení nábojů. Z tohoto důvodu budeme prozatím rozlišovat pouze dvě kategorie látek - vodiče a nevodiče (dielektrika). Do prvně jmenované kategorie zařadíme ty látky, v nichž se za dobu podstatně kratší, než je doba prováděného pozorování, ustaví rovnovážné, časově neproměnné, rozdělení náboje podmíněné konkrétním uspořádáním soustavy. Naopak do druhé kategorie zařadíme ty látky, v nichž můžeme principiálně rozložit náboj libovolným způsobem, přičemž toto rozložení zůstane v podstatě nezměněné po celou dobu pozorování.
Uspořádání elektrických nábojů bude tedy vázáno na určitá tělesa charakterizovaná příslušnou geometrií (tvarem, velikostí, polohou) a vedle sil elektrostatického pole budou na nositele elektrických nábojů působit další síly, které znemožňují těmto nositelům těleso opustit a zaručují stabilitu rovnovážného rozdělení nábojů v tělese. V případě vodivého tělesa tyto síly neovlivní v konečném důsledku rovnovážné rozdělení náboje v objemu tělesa, neboť nositelům náboje je zde dovolen volný pohyb. Zaručují pouze, že náboje nebudou těleso opouštět (nedojde k emisi nositelů náboje). V případě dielektrického tělesa budou tyto síly udržovat dané rozložení náboje v celém objemu tělesa. Později (v kapitole 3) uvidíme, že v nehomogenních vodičích (kovech, roztocích) mohou existovat síly chemické povahy (tzv. vtištěné síly), které vyvolávají pohyb nositelů náboje; v našem modelu tyto síly prozatím vyloučíme a za jedinou sílu, jejímž vlivem se elektrické náboje pohybují, budeme považovat sílu elek-trostatického pole.
Zdůrazněme ještě jednu závažnou okolnost. Experimentální skutečnosti, na něž jsme se odvolávali, se týkají pozorování makroskopických nábojů a makroskopických polí. Děláme-li na základě těchto pozorování například závěry o intenzitě elektrostatického pole v objemu vodiče nebo dielektrika, týkají se tyto závěry vlastně středních hodnot intenzity pole, které působí na nositele náboje a vyvolává jejich uspořádaný pohyb. Víme totiž, že látka, ať již vodič či dielektrikum, je tvořena molekulami a atomy, atomy opět atomovými jádry a elektrony, tedy nabitými elementárními částicemi. Uvnitř molekul, atomů a jader dochází ke komplikovaným pohybům elektrických nábojů, vznikají rychle proměnná elektrická pole o velké intenzitě. Tato mikroskopická pole není však možné postihnout ani přímým pozorováním, ani metodami výpočtů, které jsme uváděli v předchozím výkladu; k tomu účelu bychom museli znát hustotu elektrického náboje jako funkci souřadnic a času v každém bodě a každém okamžiku, nehledě na komplikovanost takových výpočtů. Budeme proto vyšetřovat makroskopická pole, která představují časovou a prostorovou střední hodnotu zmíněných polí mikroskopických. (Zákonitosti přechodu od mikroskopického pole k poli makroskopickému budou podrobněji vyšetřovány v kapitole 5.) V této souvislosti je třeba si uvědomit, že o elektrostatickém poli má smysl hovořit jen jako o poli makroskopickém; mikroskopické elektrostatické pole v přírodě neexistuje!
V tomto článku budeme studovat vlastnosti elektrostatického pole v okolí nábojů, jejichž nositeli jsou vodivá tělesa. Umístíme-li takové těleso do elektrostatického pole jiného nabitého tělesa, zjistíme, že se na tomto vodivém tělese rovněž objeví makroskopické elektrické náboje, které pozmění průběh původního elektrostatického pole. Na obrázku l.43 je schematicky znázorněna konkrétní situace. Do blízkosti kladně nabité tyče T je umístěno vodivé těleso K. Po ustavení rovnovážného stavu budou jeho části bližší tyči T nabity záporně, zatímco části vzdálenější budou nabity kladně. Celková velikost náboje izolovaného, původně nenabitého, vodivého tělesa K zůstane ovšem nulová - vzniklý kladný a záporný makroskopický náboj mají touž velikost. Uvedený jev spočívající v tom, že elektrostatické pole vyvolává existenci makroskopických nábojů na povrchu vodičů původně nenabitých, se nazývá elektrostatická indukce.
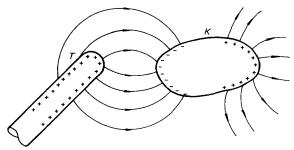
Obr. 1.43 Elektrostatická indukce.
Jev elektrostatické indukce snadno pochopíme na základě představy o existenci volných nositelů náboje na vodiči. Vložíme-li totiž vodič do elektrostatického pole, bude na každou částici nesoucí elektrický náboj působit síla daná vztahem (1.32) , jejímž účinkem se počnou volní nositelé náboje přemisťovat. Je zřejmé, že tímto způsobem dojde k separaci kladných a záporných nábojů v tělese. Za předpokladu, že na nositele náboje nepůsobí v objemu tělesa žádné další síly, musí být rovnovážné rozdělení nábojů v tělese takové, aby výsledná intenzita pole byla všude uvnitř nulová. Kdyby totiž bylo v některé části vodiče pole nenulové, museli by se volní nositelé náboje účinkem tohoto pole přemisťovat; dané rozložení náboje by tedy nemohlo být rovnovážné.
Z Gaussova zákona elektrostatiky dále plyne, že uvnitř vodiče nemohou v rovnovážném stavu existovat makroskopické náboje. Tok libovolnou uzavřenou plochou ležící uvnitř vodiče musí být totiž vzhledem k nulovosti intenzity pole vždy nulový. Z Gaussova zákona pak ihned plyne, že musí být nulovým i náboj uzavřený v libovolné ploše ležící uvnitř vodiče. V rovnovážném stavu mohou být tedy náboje rozloženy jen na povrchu vodiče. Lze je proto považovat za náboje plošně rozložené, charakterizované plošnou hustotou s(r).
Můžeme tedy shrnout:
Vložíme-li vodivé těleso do vnějšího elektrostatického pole, dojde k přeskupení jeho volných nositelů náboje tak, aby jejich vlastní pole vykompenzovalo všude v objemu vodiče původní pole vnější, takže intenzita výsledného pole E = 0. Makroskopické náboje se přitom soustředí na povrchu vodiče.[5] Jak uvidíme v článku 1.4.4, je vzniklé rozložení plošného náboje jednoznačné.
Z nulovosti intenzity pole uvnitř vodiče plyne, že elektrostatický potenciál bude v celém objemu konstantní. Celý objem vodiče tedy tvoří ekvipotenciální objem, jeho povrch tvoří ekvipotenciální plochu. Jelikož intenzita pole je vždy kolmá k ekvipotenciální ploše (viz rov. (1.66) ), bude v blízkosti vodiče vektor intenzity elektrostatického pole vždy kolmý k jeho povrchu.
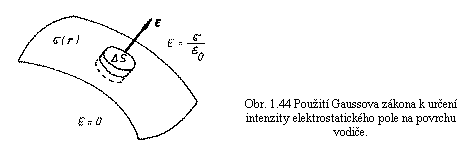
Určeme nyní hodnotu intenzity
elektrostatického pole v blízkosti povrchu vodiče. Zvolíme uzavřenou plochu ve
tvaru velmi nízkého válce a malých podstav DS libovolného tvaru, jehož osa je kolmá k
povrchu vodiče a jehož jedna podstava je umístěna vně vodiče, druhá uvnitř
(obr. 1.44). Vzhledem k rozměrům válce můžeme zanedbat nehomogenitu pole a
nehomogenitu rozložení povrchového náboje. Uvnitř této válcové plochy je tedy
uzavřen celkový náboj rovný DQ = s DS, kde s je hodnota povrchové hustoty náboje v místě válce.
Tok intenzity pole podstavou uvnitř vodiče je samozřejmě nulový, tok pláštěm
rovněž, neboť siločáry jsou rovnoběžné s osou válce. Zbývá tedy tok podstavou
přimykající k povrchu vodiče zevně rovný DF
= E DS. Z Gaussova zákona pak okamžité dostáváme
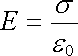 . . |
(1.185) |
Uvedené tvrzení se někdy nazývá Coulombovou větou. Pozoruhodné na něm je zejména to, že ačkoliv elektrostatické pole vně vodiče je vytvářeno celkovým rozložením nábojů na povrchu vodiče a dalších těles, je v blízkosti povrchu plně určeno lokální hodnotou hustoty v daném bodě povrchu. (Všimněme si, že z výrazu (1.185) vyplývá opět nespojitost normálové složky intenzity s/e0.) Siločáry elektrostatického pole dopadají zvnějšku kolmo k povrchu vodiče tam, kde je soustředěn záporný plošný náboj, a vycházejí opět kolmo k povrchu tam, kde je soustředěn kladný plošný náboj.
Toto chování vodičů ve vnějším elektrostatickém poli má závažné praktické důsledky. Jsou-li na povrchu vodiče ostré výstupky nebo hroty, vzniká v jejich blízkosti silně nehomogenní elektrostatické pole. Elektrické siločáry, které stále zůstávají kolmé k povrchu, zde prudce mění směr a u povrchu se zhušťují. Tím rostou podle vztahu (1.50) i hodnoty gradientu potenciálu a vznikají zde mezi blízkými body vysoká napětí.[6]


Vytvoříme-li uvnitř vodiče dutinu, bude i v této dutině zůstávat intenzita pole nulová (pokud v ní nebudou přítomny izolované makroskopické náboje). Hovoříme proto někdy poněkud nepřesně o "stínicím účinku vodičů". Pole v dutině obklopené vodičem není totiž v pravém slova smyslu odstíněno, nýbrž vykompenzováno polem povrchových nábojů. Důležité je, že tento stav zůstane nezměněn i při změnách celkového náboje vodiče a průběhu vnějšího pole.
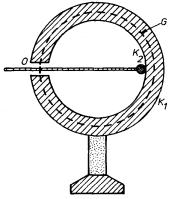
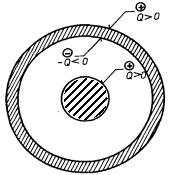
Dalším důsledkem této vlastnosti vodičů je možnost postupně zvětšovat povrchový náboj dutého vodiče, a tím i jeho potenciál tak, že náboj přivádíme na jeho vnitřní povrch. Na obrázku 1.45 je znázorněna dutá vodivá koule K1 s malým otvorem O upevněná na izolovaném podstavci. Vnášíme-li do dutiny koule náboj malé vodivé kuličky K2, jíž se dotkneme vnitřního povrchu koule K1, bude tento náboj okamžitě převeden na vnější povrch koule. V okamžiku doteku vytvoří totiž oba vodiče K1, K2 jediné vodivé těleso, v jehož vnitřním objemu nemohou makroskopické náboje existovat. Vedeme-li Gaussovu plochu G stěnou duté koule K1, bude tok touto plochou nulový a stejně tak makroskopický náboj uvnitř této plochy. Tímto způsobem můžeme kouli nabíjet teoreticky neomezeně velkým nábojem; praktické omezení je dáno průrazným napětím, které závisí na geometrickém uspořádání, na prostředí zaplňujícím kouli a jejím okolí. Na tomto jevu je například založen princip van de Graaffova generátoru (viz příklad 6.3.2a).
Tok uvedenou Gaussovou plochou G musí být nulový i v okamžiku vložení makroskopického náboje do dutiny koule před tím, než se dotkneme vnitřního povrchu. To je ovšem možné jen tak, že se na vnitřním povrchu koule bude indukovat stejně velký náboj opačného znamení. Po doteku tento náboj z vnitřního povrchu zmizí. Situace je znázorněna na obr. 1.46 pro případ, že dutá koule není elektricky nabitá. Bude-li mít koule elektrický náboj, budou se povrchové náboje na vnitřním a vnějším povrchu lišit, přičemž náboj na vnitřním povrchu musí vždy kompenzovat izolovaný náboj uvnitř dutiny. Uvedená úvaha zůstává samozřejmě v platnosti i pro vodiče libovolného tvaru, je-li jeden z nich obklo-pen vodičem druhým.
V předchozím článku jsme ukázali, že v důsledku přítomnosti dostatečného počtu volných nositelů náboje se ve vodiči vloženém do elektrostatického pole ustaví rovnovážný stav, při kterém je intenzita pole v celém jeho objemu nulová. Dále bylo pomocí Gaussova zákona ukázáno, že uvnitř vodičů nemohou v rovnovážném stavu existovat od nuly různé makroskopické náboje. Gaussův zákon představuje však zobecnění zákona Coulombova, přičemž podstatným tvrzením obsaženým v Coulombově zákoně, které jsme při odvozování Gaussova zákona využívali, je to, že síla působící mezi dvěma bodovými náboji ubývá se čtvercem vzdáleností. Skutečnost, že makroskopické náboje se nacházejí v rovno-vážném stavu jen na povrchu vodičů, můžeme proto považovat za důsledek Coulombova zákona.
Obráceně lze ukázat, že jestliže náboje jsou v rovnovážném stavu jen na povrchu vodičů, musí intenzita pole bodového náboje ubývat se čtvercem vzdálenosti. Obě tvrzení jsou tedy ekvivalentní. Víme, že Coulombův zákon byl experimentálně potvrzen metodou torzních vah, přičemž přesnost tohoto experimentu není příliš velká. S mnohem větší přesností je možné prokázat, že náboje ve vodičích se nacházejí v rovnovážném stavu na povrchu - tím je však vzhledem k ekvivalentnosti obou tvrzení experimentálně ověřen Coulombův zákon. Je zajímavé, že této skutečnosti si byl vědom již Cavendish a ten také ještě před formulací Coulombova a Gaussova zákona zákon převrácených čtverců tímto způsobem experimentálně nepřímo ověřil.
Provedeme nyní důkaz ekvivalence tvrzení.
1. "Intenzita pole bodového náboje ubývá se čtvercem vzdálenosti" a
2. "Makroskopické náboje na vodičích se mohou v rovnovážném stavu nacházet pouze na povrchu" pro případ kulového vodiče. Z důvodu symetrie koule je totiž možné soudit i na symetrii rozložení náboje, což usnadňuje provedení důkazu. Důkaz je ovšem možné zobecnit i na vodič libovolného tvaru.

Uvažujme tedy kulový vodič poloměru R nesoucí náboj Q. V rovnovážném stavu musí být intenzita pole uvnitř vodiče nulová, jinak by docházelo k pohybu volných nositelů náboje. Vycházíme-li z platnosti zákona převrácených čtverců, a tedy i zákona Coulombova a Gaussova, plyne odtud, že v objemu vodiče nemohou existovat makroskopické náboje, a musí tedy sídlit pouze na povrchu. Stačí totiž vést uvnitř vodiče libovolnou Gaussovu plochu, tok intenzity touto plochou bude nulový a nulový bude i náboj uvnitř libovolné uzavřené plochy v objemu vodiče. Tím jsme dokázali, že z tvrzení l plyne tvrzení 2.
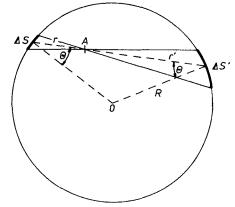
Vyjděme nyní ze skutečnosti, že náboj je rozprostřen na povrchu koule. Ze symetrie vyplývá, že hustota náboje bude na povrchu konstantní a bude rovna s = Q/4pR2. Budeme nyní počítat intenzitu pole pomocí této hustoty v libovolném bodě A uvnitř koule. Celý objem koule rozdělíme na dvojice souosých kuželů se společným vrcholem v bodě A a stejnými malými vrcholovými prostorovými úhly DW (viz obr. 1.47). Uvedené kuželové plochy rozdělí celý povrch vodiče na malé plošky DS a DSc. Výsledné pole v daném bodě A bude pak podle principu superpozice dáno sumou příspěvků od nábojů DQ a DQc na všech těchto ploškách.
Budeme nyní předpokládat, že intenzita pole E(r) bodového náboje je úměrná jeho velikosti, míří ve směru průvodiče a ubývá monotónně se vzrůstající vzdáleností r. Tento pokles nechť je popsán neznámou funkcí f(r), takže podle uvedených předpokladů můžeme napsat
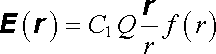 , , |
(1.186) |
kde C1 je konstanta.
Má-li být v bodě A celková intenzita pole nulová, musí se vyrušit příspěvky způsobené náboji DQ, DQc na obou ploškách DS, DSc v každé dvojici, tj. musí platit vztahy
 . . |
(1.187) |
Kdyby
totiž pro některou dvojici kuželů platilo například
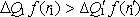 ,
musela by být takto vzniklá složka intenzity pole vykompenzována jinými
dvoji-cemi kuželů a pro ně by muselo platit
,
musela by být takto vzniklá složka intenzity pole vykompenzována jinými
dvoji-cemi kuželů a pro ně by muselo platit
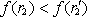 při
při
 . To však není možné vzhledem k monotónnosti
funkce f(r).
. To však není možné vzhledem k monotónnosti
funkce f(r).
Z obrázku 1.47 je dále patrné, že DQ = s DS = s r2 DW / cos q , DQc = s rc2 DW / cos q. Po dosazení do vztahů (1.187) dostaneme tudíž podmínku
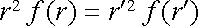 . . |
(1.188) |
Jelikož však jsou poloměr koule R i poloha bodu A uvnitř koule voleny libovolně, musí pro každou hodnotu vzdálenosti platit
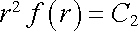 , , |
(1.189) |
kde C2 je konstanta. Funkce f(r) má tedy tvar f(r) = C2 / r2, takže po dosazení do vztahu (1.186) dostaneme tvar Coulombova zákona. Tím jsme dokázali, že i z tvrzení 2 plyne zpětně tvrzení l.
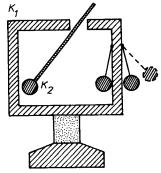
Experimentální ověření skutečnosti, že náboje jsou rozmístěny v rovno-vážném stavu pouze na povrchu vodičů, má tedy principiální význam. Kvali-tativně se o něm přesvědčíme například pokusy s Faradayovou klecí. Uvažujme izolovaný dutý vodič K1, s malým otvorem podle obr. 1.48. Nechť jsou podél stěn vodiče zavěšeny na nevodivých vláknech dvě velmi lehké vodivé kuličky. Může jít například o kuličky bezové, či zhotovené z pěnového polystyrenu, na nichž je nanesena tenká vodivá, třeba grafitová vrstva. Vložíme-li nyní do dutiny izolovaný nabitý vodič K2 a dotkneme se jím vnitřní stěny dutiny, zjistíme dvě skutečnosti. Za prvé vodič K2 neponese po vyjmutí z dutiny žádný náboj. Za druhé vnější kulička se vychýlí ze své původní polohy do polohy čárkovaně vyznačené na obrázku, zatímco vnitřní kulička zůstane v původní poloze. Vodič K2 předal svůj náboj vodiči K1, neboť v okamžiku doteku tvořily oba vodiče jediné vodivé těleso, přičemž vodič K2 byl umístěn v jeho vnitřním prostoru, kde nemůže existovat makroskopický náboj. Předaný náboj se pak okamžitě přemístil na vnější povrch vodiče K1. Vnější kulička získala tedy náboj stejného znamení jako vodič K1 a v důsledku silového působení mezi těmito náboji zaujala novou polohu. Vnitřní kulička, vzhledem k tomu, že se dotýkala vnitřní stěny dutiny, žádný náboj získat nemohla, a proto zůstala ve své původní poloze.
Jeden z nejpřesnějších experimentů tohoto druhu byl proveden S. J. Plimptonem a W. E. Lawtonem v r. 1936.[7] Zmínění autoři použili kvazistatické metody, jejíž schematické uspořádání je uvedeno na obr. 1.49. Sestává z izolované kovové vnější koule A o průměru asi 1,5 m, která je periodicky nabíjena z generátoru na potenciál 3 000 V. Do této koule je izolovaně vložena vnitřní koule B o průměru asi 1,2 m. Součástí povrchu této koule je stínění elektronkového zesilovače Z, který je do ní vložen a kterým je možné detekovat případné změny napětí mezi oběma koulemi. Pro zvýšení citlivosti měření je na výstup zesilovače připojen galvanometr G, jehož frekvence vlastních kmitů měrného systému souhlasí s frekvencí generátoru nabíjejícího vnější kouli (asi 2 Hz). Výchylku galvanometru je možné pozorovat opticky pomocí dalekohledu D okénky O1 a O2 . Okénko O1 je přitom vyplněno vodivým průhledným roztokem, takže celistvost koule A zůstává neporušena. Uvedené kvazistatické uspořádání dovoluje dosáhnout velké citlivosti, neboť již velmi malé periodické změny napětí o frekvenci rovné vlastní frekvenci galvanometru jsou schopny vyvolat znatelné výchylky galvanometru. Kromě toho dovoluje střídavá metoda vyloučit některé parazitní vlivy, které by omezovaly přesnost výsledku při měření statickými metodami.
Citovaní autoři byli schopni detekovat změny napětí mezi koulemi A a B rovné 10-6 V. Ani při této citlivosti však nebyly pozorovány žádné rozdíly v potenciálu obou koulí. Na základě uvedeného výsledku je exponent ve jmenovateli Coulombova zákona určen s přesností 2.10-7 procent, tedy o sedm řádů přesněji než u experimentu Coulombova.


Na začátku kapitoly o elektrostatice jsme se zabývali vlastnostmi soustavy bodových nábojů rozmístěných v prostoru. Nyní budeme uvažovat reálnější soustavu tvořenou N vodivými tělesy. Každé z těchto těles je charakterizováno určitou geometrií, tj. tvarem a polohou v prostoru; jeho povrch tvoří uzavřenou plochu Si, i = 1,2,..., N. Nechť jednotlivé vodiče nesou náboje Qi (některé z těchto nábojů mohou být i nulové). Dále víme, že intenzita pole uvnitř každého z vodičů bude rovna nule, náboje budou rozloženy na povrchu s hustotou si(r) a povrch vodiče bude představovat ekvipotenciální plochu o potenciálu ji (viz obr. 1.50). Intenzita pole u povrchu každého vodiče je vázána na povrchovou hustotu náboje vztahem (1.185) a splňuje podmínku, že tok intenzity pole Gaussovou plochou G těsně přimykající k povrchu vodiče je
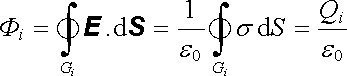 . . |
(1.190) |
Z teoretického hlediska vznikají nyní dvě otázky. Za prvé, je-li pro libovolnou soustavu vodičů takové rozložení nábojů po jejich povrchu vždy možné, a za druhé, je-li uvedenými požadavky rozložení náboje jednoznačně určeno.
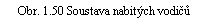
Řešením první otázky se nebudeme zabývat. Spokojíme se s fyzikálním názorem, podle něhož lze očekávat, že libovolné náboje přivedené na libovolnou soustavu vodičů mají možnost rovnovážného statického rozložení. Odpověď na druhou otázku však již není tak zřejmá. Není například jasné, jestli při různém pořádku přivádění nábojů na jednotlivé vodiče není obecně možné jejich různé rovnovážné rozložení, které by ovšem mohlo vést k různému průběhu pole v okolním prostoru. Ukazuje se však, že tato nejednoznačnost není obecně možná,[8] neboť by vedla ke sporu s obecnými vlastnostmi potenciálu probranými v článku 1.2.7.
Statické, rovnovážné rozložení nábojů na libovolné soustavě vodičů je tedy jednoznačně dáno velikostí těchto nábojů, velikostí, tvarem a rozmístěním vodičů v prostoru. Tímto rozložením je podle vztahu (1.70b) také až na aditivní konstantu jednoznačně určen průběh potenciálu ve všech bodech prostoru. Speciálně jsou velikostí nábojů určeny také potenciály všech vodičů. Problém nalezení elektrostatického pole soustavy nabitých vodičů je tedy principiálně plně rozřešen. Budeme-li znát hustoty nábojů na povrchu těchto vodičů, můžeme potenciál vždy vypočítat pomocí vztahu (1.70b) .
Nalezení této hustoty pouze z podmínky konstantnosti potenciálu uvnitř vodičů je však velmi obtížné. Proto volíme jiný, schůdnější postup využívající toho, že potenciál musí ve všech bodech prázdného prostoru (tj. všude tam, kde hustota nábojů je nulová) splňovat Laplaceovu rovnici. Na základě toho, co o elektrostatickém poli vodičů již víme, můžeme totiž formulovat jednoduché podmínky, které určují jednoznačně hodnotu potenciálu ve všech bodech prostoru. Podaří-li se nám ukázat, že tyto podmínky také jednoznačně určují řešení Laplaceovy rovnice, bude problém hledání potenciálu soustavy vodičů převeden na problém hledání řešení Laplaceovy rovnice vyhovujícího určitým vedlejším podmínkám. Úloha tohoto druhu se nazývá základní úlohou elektrostatiky.
Pokusíme se nyní
formulovat uvedené podmínky. Především víme, že potenciál musí mít konstantní
hodnotu v celém objemu každého vodiče. Protože potenciál je na povrchu vodiče
spojitý (viz článek 1.2.4), stačí tedy znát hodnotu potenciálu
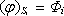 na povrchu každého vodiče. Pokud jsou
zadány velikosti nábojů každého z vodičů, musí potenciál na povrchu každého
vodiče vyhovovat podmínce
(1.190)
, kde položíme E = - grad j
na povrchu každého vodiče. Pokud jsou
zadány velikosti nábojů každého z vodičů, musí potenciál na povrchu každého
vodiče vyhovovat podmínce
(1.190)
, kde položíme E = - grad j
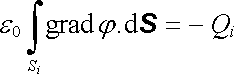 |
(1.191) |
(vzhledem ke spojitosti potenciálu na povrchu vodiče můžeme
integrovat přímo po povrchu Si).
Zadáním velikosti nábojů všech vodičů je, jak víme, potenciál v celém
prostoru určen až na aditivní konstantu. Jsou-li dále všechny vodiče
v konečnu, můžeme vždy požadovat, aby platilo
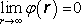 .
.
V praxi se stává, že máme řešit elektrostatické pole vodičů rozmístěných v dutině vodivého tělesa. Průběh pole vně tohoto tělesa nás přitom nezajímá. Pak můžeme podmínku nulovosti potenciálu v nekonečnu nahradit podmínkou nulovosti potenciálu na vodivé obálce. Tím vyloučíme vnější prostor z našich úvah a jednoznačnost potenciálu bude opět zaručena zadáním nábojů, resp. potenciálů na povrchu jednotlivých vodičů.
Základní úlohu elektrostatiky můžeme nyní formulovat takto:
Najít elektrostatický potenciál j (r) jako funkci definovanou a spojitou se svými derivacemi až do druhého řádu v daném uzavřeném objemu nebo v celém prostoru, která vyhovuje Laplaceově rovnici
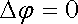 |
a okrajovým podmínkám
1.
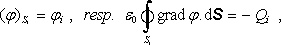
2.
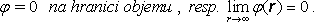 (ji,
popř. Qi, jsou
přitom zadané hodnoty.)
(ji,
popř. Qi, jsou
přitom zadané hodnoty.)
lokální extrém v prázdném
prostoru (viz článek 1.2.7), plyne odtud, že jc
musí být všude rovno nule, a tedy j1 = j2 .
Zbývá ukázat, že
existuje nejvýše jedno řešení Laplaceovy rovnice, které vyhovuje udaným
okrajovým podmínkám. Toto jednoznačně určené řešení bude pak představovat
skutečné rozložení elektrostatického potenciálu soustavy nabitých vodičů v
prostoru. Důkaz jednoznačnosti provedeme sporem. Nechť existují dvě různá
řešení základní úlohy elektrostatiky j1, j2. Potom funkce jc = j1
- j2 bude
rovněž splňovat Laplaceovu rovnici (díky její linearitě). Na všech vodičích
bude přitom platit okrajová podmínka
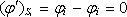 a samozřejmě
a samozřejmě
 . Protože řešení Laplaceovy rovnice
nemůže mít
. Protože řešení Laplaceovy rovnice
nemůže mít
Řešení Laplaceovy rovnice hledáme obvykle metodami matematické fyziky, které zde nemůžeme podrobně rozebírat. Často přitom využíváme právě jednoznačnosti řešení této úlohy, tedy okolnosti, že řešení je okrajovými podmínkami plně určeno. Uvažme například libovolné elektrostatické pole. Vyplňme dále část prostoru vodivým prostředím tak, aby povrch vodivého tělesa byl totožný s některou ekvipotenciální plochou původního pole. Předpokládejme dále, že celý náboj, který byl původně uzavřen v uvažované ekvipotenciální ploše, přejde na naše vodivé těleso. Je zřejmé, že původní pole splňuje na tomto vodiči okra-jovou podmínku 1. Z věty o jednoznačnosti potenciálu pak plyne, že původní pole ve vnějším prostoru zůstane zachováno i po zařazení vodiče.
Okrajovou podmínku 1 na určité vodivé ploše můžeme tedy někdy výhodně nahradit rozložením myšlených nábojů v té části prostoru, kde nás řešení zá-kladní úlohy elektrostatiky nezajímá. Tomuto přístupu se říká metoda elektro-statického zobrazení. (O jejím použití viz příklady 1.4.7a až c.)
Uvažujme izolované vodivé těleso nesoucí náboj Q. Potenciál vytvořený tímto tělesem v okolním prostoru označíme j(r). Ptáme se, jak se změní potenciál, jestliže na uvažované těleso přivedeme nový náboj Q' = AQ, kde A je konstanta. Podle předchozího článku je hledaný potenciál určen vztahem j´(r) = Aj(r), neboť zřejmě splňuje všechny požadované podmínky. Platí tedy vztah
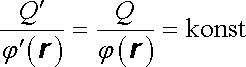 . . |
(1.192) |
Poměr mezi velikostí náboje na uvažovaném tělese a hodnotou potenciálu v da-ném bodě je tedy funkcí pouze geometrických parametrů tělesa a daného bodu. Speciálně, označíme-li j0 hodnotu potenciálu na povrchu tělesa odpovídající náboji Q, můžeme psát
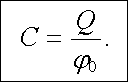 |
(1.193) |
Veličina C, která rovněž závisí pouze na geometrických parametrech daného izolovaného tělesa (jeho velikosti a tvaru), se nazývá jeho kapacita. Kapacita osamoceného vodiče vyjadřuje tedy jeho schopnost shromažďovat elektrický náboj. Těleso o menší kapacitě bude daným nábojem přivedeno na vyšší potenciál než těleso o větší kapacitě.
V Mezinárodní soustavě jednotek bude mít jednotkovou kapacitu těleso, které se nábojem jednoho coulombu přivede na potenciál jednoho voltu. Tato jednotka se nazývá farad (F). Jelikož je pro praktické použití příliš velká, užívá se hlavně odvozených jednotek mikrofarad (mF), 1 mF = 10-6 F, popř. nanofarad (nF), l nF = 10-9 F, či pikofarad (pF), l pF = 10-12 F.
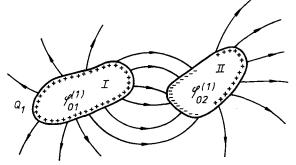
Obr. 1.51 Rozdělení povrchových nábojů v soustavě nabitého a nenabitého vodivého tělesa.
Nyní rozšíříme
naše úvahy o vztahu mezi náboji a potenciály na soustavu nabitých vodičů.
Uvažme nejdříve dvě vodivá tělesa, z nichž jedno nese náboj Q1 a druhé je nenabité. Je-li
první těleso v prostoru osamoceno, bude pro jeho potenciál platit
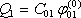 , kde
, kde
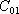 je jeho kapacita. Zaujme-li nyní druhé, nenabité,
těleso žádanou polohu v prostoru, nastane situace znázorněná na obr. 1.51
a na druhém tělese dojde k rozdělení indukovaných nábojů. Současně se musí
ovšem přerozdělit náboj Q1
na povrchu prvního tělesa, aby obě tělesa měla opět konstantní potenciál. Nové
elektrostatické pole této soustavy bude mít v prostoru potenciál daný
funkcí j(r) a potenciály obou těles budou
je jeho kapacita. Zaujme-li nyní druhé, nenabité,
těleso žádanou polohu v prostoru, nastane situace znázorněná na obr. 1.51
a na druhém tělese dojde k rozdělení indukovaných nábojů. Současně se musí
ovšem přerozdělit náboj Q1
na povrchu prvního tělesa, aby obě tělesa měla opět konstantní potenciál. Nové
elektrostatické pole této soustavy bude mít v prostoru potenciál daný
funkcí j(r) a potenciály obou těles budou
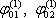 . Změníme nyní náboj Q1 na hodnotu
. Změníme nyní náboj Q1 na hodnotu
 .
Funkce jc(r) = Aj(r)
nabývá na obou tělesech hodnot
.
Funkce jc(r) = Aj(r)
nabývá na obou tělesech hodnot
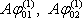 a zřejmě vyhovuje okrajovým podmínkám pro
novou hodnotu náboje Q'. Podle věty o
jednoznačnosti popisuje tedy tato funkce nový průběh potenciálu. Podobně jako v
případě jediného tělesa musí tedy existovat konstanty dané pouze geometrickým
uspořádáním, které určují úměrnost mezi potenciály těles a nábojem Q1. Označíme je B11, B21 a zmíněnou úměrnost zapíšeme ve tvaru
a zřejmě vyhovuje okrajovým podmínkám pro
novou hodnotu náboje Q'. Podle věty o
jednoznačnosti popisuje tedy tato funkce nový průběh potenciálu. Podobně jako v
případě jediného tělesa musí tedy existovat konstanty dané pouze geometrickým
uspořádáním, které určují úměrnost mezi potenciály těles a nábojem Q1. Označíme je B11, B21 a zmíněnou úměrnost zapíšeme ve tvaru
 . . |
(1.194) |
Opakujeme-li stejnou úvahu pro případ, že první těleso je
bez náboje a druhé nese náboj Q2 , dokážeme existenci konstant B12 , B22 vyjadřujících vztah mezi analogickými hodnotami
potenciálu
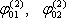 a nábojem Q2
. Tedy
a nábojem Q2
. Tedy
 . . |
(1.195) |
Obecný případ, ve kterém první těleso nese náboj Q1 a druhé těleso náboj Q2, můžeme považovat za superpozici právě vyšetřovaných speciálních případů. Pro potenciály j 01, j 02 obou těles bude tedy podle (1.194) a (1.195) platit
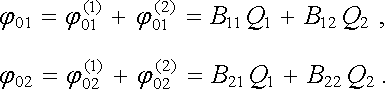 |
(1.196) |
Provedený postup můžeme dále reprodukovat pro libovolný počet těles. Uvažujeme-li soustavu složenou z N vodičů nesoucích postupně náboje Q1, Q2,..., QN a označíme-li j01, j02,...,j0N jejich potenciály, můžeme místo (1.196) psát soustavu lineárních vztahů
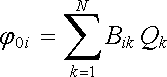 . . |
(1.197) |
Konstanty Bik , které jsou určeny rozměry, tvarem a vzájemnými polohami všech vodičů, se nazývají potenciálové koeficienty.
Potenciálové koeficienty mají některé obecné vlastnosti. V článku 1.4.6 dokážeme z energetické úvahy, že matice Bik je symetrická, tj., že platí
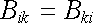 . . |
(1.198) |
Vzájemnou závislost mezi náboji a potenciály vodičů určuje tedy N2 konstant, z nichž pouze N(N + 1)/2 je nezávislých.
Vztahy (1.197) představují soustavu lineárních rovnic o N neznámých Qk s pravou stranou (nehomogenních). Je-li determinant matice Bik nenulový, má tato soustava právě jedno řešení. (To odpovídá fyzikálnímu předpokladu o tom, že náboje a potenciály všech vodičů jsou vzájemně jednoznačně určeny.) Potom můžeme soustavu rovnic (1.197) vyřešit vzhledem ke Qk a napsat
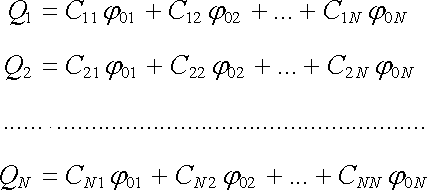 |
(1.199) |
neboli
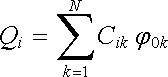 . . |
(1.199a) |
Diagonální prvky matice Cik, Cii označujeme jako kapacitní koeficienty pří-slušných vodičů, nediagonálním prvkům Cik, i^1k, říkáme influenční koeficienty. Pomocí (1.198) lze snadno ukázat, že matice Cik je opět symetrická. Hodnoty kapacitních i influenčních koeficientů udáváme ve faradech.
Kapacitní koeficient Cii daného vodiče je ovšem různý od jeho kapacity C jako osamoceného vodiče. Na osamoceném vodiči kladný náboj vyvolává kladný potenciál, takže veličina C je vždy kladná. Přítomnost dalších vodičů vede k poklesu potenciálu na tomto vodiči, takže Cii > C; přitom nemůže dojít ke změně znaménka potenciálu. Hodnoty obou veličin Cii, C budou tím bližší, čím méně se bude uplatňovat vliv ostatních vodičů, tj. čím menší budou hodnoty příslušných influenčních koeficientů.
Pokud jde o influenční koeficienty, lze ukázat, že jejich hodnoty jsou Cik lb 0. Kladně nabitý vodič indukuje a váže na bližší straně druhého vodiče záporný náboj; je-li tento vodič například uzemněn (j02 = 0), bude kladný náboj odveden do země. Influenční koeficient, který představuje podíl záporného indukovaného náboje na druhém vodiči a kladného potenciálu prvního vodiče, bude tedy záporný. Influenční koeficient může být roven nule například tehdy, jsou-li dva vodiče navzájem zcela odstíněny vodivou plochou. Naopak influenční koeficient mezi dvěma vodiči, z nichž jeden zcela obklopuje druhý, bude roven kapacitě vnitřního vodiče s opačným znaménkem.
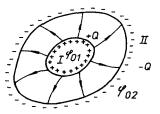
Tento poslední případ nás přivádí k důležitému uspořádání dvou vodičů, které nazýváme kondenzátorem. Předpokládejme nejprve, že první z těchto vodičů je izolovaně umístěn v dutině druhého vodiče (obr. 1.52). Náboj Q přivedený na první vodič indukuje na vnitřní stěně druhého vodiče náboj - Q. Všechny siločáry, které vycházejí z kladných nábojů na jednom z vodičů končí u nábojů na druhém vodiči a elektrostatické pole je uzavřeno v dutině mezi oběma vodiči. Přitom nezáleží na nábojích na vnějším povrchu druhého vodiče či na vnějších polích. Mezi vodiči bude existovat nenulový rozdíl potenciálů, tedy napětí U = j01 - j02. Podle (1,199) můžeme psát
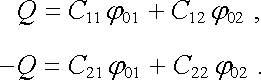 |
(1.200) |
Ze čtyř neznámých Cik jsou pouze tři nezávislé, neboť C12 = C21. Bude-li náboj Q = 0, bude vnitřní vodič součástí ekvipotenciálního objemu tvořeného dutinou vnějšího vodiče a j01 = j02 . Tak dostáváme C11 = - C12 = - C21 = C22 = C.
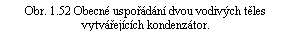
Vidíme tedy, že všechny čtyři konstanty Cik mohou být vyjádřeny pomocí jediné konstanty C, kterou nazveme kapacita kondenzátoru. Z rovnic (1.200) pak platí
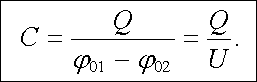 |
(1.201) |
Příslušné dva vodiče je zvykem nazývat elektrodami kondenzátoru.
Hodnota kapacity kondenzátoru (měříme ji opět ve faradech) je určena rozměry, tvarem a vzájemnou polohou obou vodičů. Jak uvidíme dále, kapacitu kondenzátoru je možno zvětšit i tím, vyplníme-li prostor mezi elektrodami vhodnou nevodivou látkou (dielektrikem). V praxi se k uvedenému účelu používá například papír, slída, keramika, některé polymery a podobně.
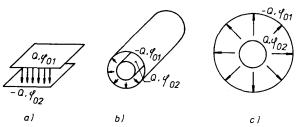
Obr. 1.53 Kondenzátory: a) deskový, b) válcový, c) kulový.
Kapacita osamoceného vodiče, kapacita kondenzátoru, kapacitní a influenční koeficienty jsou veličiny stejné fyzikální povahy a měří se v týchž jednotkách. Kondenzátor má kapacitu jednoho faradu, jestliže nábojem jednoho coulombu získají jeho elektrody napětí jednoho voltu.
Z hlediska praktického použití nelze ovšem dobře konstruovat kondenzátor tak, aby jedna elektroda zcela obklopovala druhou. Volí se proto různé konstrukce, u nichž je uvedená podmínka splněna pouze přibližně. Takové kondenzátory pak samozřejmě nejsou úplně nezávislé na vnějších polích a tam, kde siločáry opouštějí prostor mezi elektrodami, se projevují tzv. okrajové efekty. Na obrázku 1.53 jsou znázorněna nejtypičtější geometrická uspořádání elektrod kondenzátoru deskového, válcového a kulového.
Všimněme si blíže kondenzátoru deskového. V ideálním případě představuje soustavu dvou rovnoběžných vodivých rovin ve vzájemné vzdálenosti d. Jak víme z příkladu 1.2.9c, jsou-li takové roviny nabity nesouhlasnými náboji s konstantní plošnou hustotou náboje s, je pole soustředěno pouze v prostoru mezi nimi, je homogenní a má velikost E = s / e0. Je-li záporně nabitá deska uzemněna, bude potenciál kladně nabité desky roven napětí mezi nimi U = E d.
Ve skutečnosti nemohou mít desky kondenzátoru podobu nekonečných rovin, ale jsou omezeny na konečnou plochu S . Je-li vzdálenost d mezi deskami malá ve srovnání s rozměry desek, můžeme pole mezi nimi považovat přibližně za homogenní a použít výrazy pro dvojici nekonečných rovin. Uvážíme-li, že s = Q / S, dostáváme
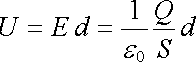 . . |
(1.202) |
Kapacita deskového kondenzátoru je tedy rovna
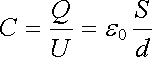 |
(1.203) |
a je tím větší, čím je větší plocha desek a čím je menší
vzdálenost mezi nimi. Běžné používaný vzorec pro kapacitu
(1.203)
platí tím
přesněji, čím menší je poměr mezi vzdáleností desek d a lineárním
rozměrem
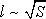 , tj. čím menší roli hrají okrajové
efekty. Přibližně lze odhadnout, že při poměru d / l = 0,1 dává vzorec
(1.203)
chybu asi 20 %, při d / l = 0,01 asi 2 % [5]. Na obrázku 1.54 je
znázorněno pole deskového kondenzátoru a průběh siločar na jeho okrajích.
, tj. čím menší roli hrají okrajové
efekty. Přibližně lze odhadnout, že při poměru d / l = 0,1 dává vzorec
(1.203)
chybu asi 20 %, při d / l = 0,01 asi 2 % [5]. Na obrázku 1.54 je
znázorněno pole deskového kondenzátoru a průběh siločar na jeho okrajích.

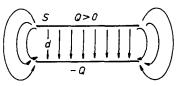
V praxi je často třeba vypočítat výslednou kapacitu několika kondenzátorů, jejichž elektrody jsou určitým způsobem spojeny. Všimneme si této úlohy pro dva speciální případy - pro tzv. paralelní a sériové spojení kondenzátorů. Na obrázku 1.55a je schematicky znázorněno paralelní spojení N kondenzátorů, které vznikne vzájemným propojením odpovídajících si elektrod všech konden-zátorů (kondenzátory jsou znázorněny obvyklou schematickou značkou). Elektrody výsledného kondenzátoru jsou tedy složeny z elektrod všech N kondenzátorů, na všech kondenzátorech je stejné napětí a náboje na deskách Qi (i = l,..., N) se sčítají ve výsledný náboj Q:
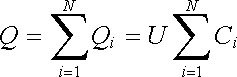 . . |
(1.204) |
Výsledná kapacita je dána součtem kapacit jednotlivých kondenzátorů
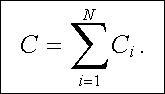 |
(1.205) |

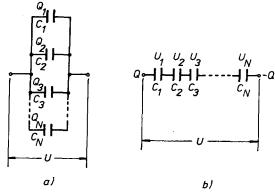
Na obrázku 1.55b je schematicky znázorněno sériové zapojení N kondenzátorů. Toto spojení vznikne postupným propojením dvojic elektrod různých kondenzátorů tak, že všechny kondenzátory jsou uspořádány v řadě. Elektrody výsledného kondenzátoru jsou potom tvořeny volnými elektrodami prvního a posledního kondenzátoru. Je zřejmé, že napětí U na výsledném kondenzátoru je rovno součtu napětí Ui (i = l,..., N) na jednotlivých kondenzátorech. Předpokládejme, že kondenzátory nebyly před spojením nabity. Potom náboj Q přivedený na volnou elektrodu prvního kondenzátoru indukuje na druhé elektrodě náboj - Q, čímž vznikne náboj Q na první elektrodě druhého kondenzátoru. Postupujeme-li tak celou řadou, dostáváme výsledný náboj - Q na volné elektrodě posledního kondenzátoru. Elektrody všech kondenzátorů nesou tedy náboj stejné velikosti. Proto platí
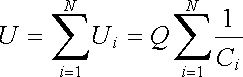 , , |
(1.206) |
takže pro výslednou kapacitu C dostaneme
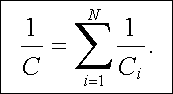 |
(1.207) |
Převrácená hodnota výsledné kapacity kondenzátorů v sériovém spojení je rovna součtu převrácených hodnot kapacity jednotlivých kondenzátorů.
V článku 1.1.5 jsme odvodili výraz pro interakční energii soustavy bodových nábojů, v článku 1.2.8 jsme tento pojem zobecnili pro libovolně rozložené náboje a zjistili jsme, že tuto energii můžeme vyjádřit též jako prostorově rozloženou energii elektrostatického pole. Původ této energie jsme přitom spatřovali v práci, kterou bylo nutné vykonat k tomu, aby soustava nábojů vznikla, tedy aby náboje po překonání elektrostatických sil byly uvedeny do svých výsledných poloh.
Soustava nabitých
vodičů může být rovněž charakterizována energií potřebnou k jejímu vytvoření.
Určeme nejdříve práci, kterou vykonáme při nabíjení jednoho osamoceného vodiče
kapacity C. Předpokládejme, že vodič
je již nabit určitým nábojem Q' na
potenciál
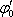 . Přivedeme-li na vodič nějaký malý
náboj DQc, vykonáme
práci
. Přivedeme-li na vodič nějaký malý
náboj DQc, vykonáme
práci
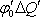 .
K nabití vodiče na celkový náboj Q je
tedy nutné vynaložit práci
.
K nabití vodiče na celkový náboj Q je
tedy nutné vynaložit práci
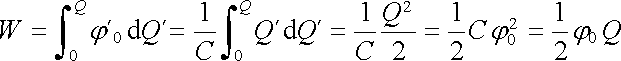 . . |
(1.208) |
Přejděme nyní k obecnému případu soustavy N vodičů nesoucích náboje Qi, a majících potenciály j0i, i = l ,..., N. Mají-li
vodiče v daném okamžiku potenciály
 a nabíjíme-li je malými náboji
a nabíjíme-li je malými náboji
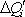 ,
konáme práci rovnou
,
konáme práci rovnou
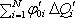 .
Abychom mohli tento výraz snadněji integrovat, vyjdeme z předpokladu, že
výsledná práce nebude záviset na postupu nabíjení jednotlivých vodičů (podobně
jako u soustavy bodových nábojů nezávisela na postupu jejich sbližování). Potom
můžeme předpokládat například, že všechny vodiče nabíjíme od počátku současně,
přičemž rychlost nabíjení jednotlivých vodičů je úměrná konečnému náboji Qi , takže nabíjení bude i
současně ukončeno. Matematicky můžeme tuto situaci vyjádřit tak, že okamžité
potenciály a náboje jsou v každém okamžiku úměrny výsledným hodnotám:
.
Abychom mohli tento výraz snadněji integrovat, vyjdeme z předpokladu, že
výsledná práce nebude záviset na postupu nabíjení jednotlivých vodičů (podobně
jako u soustavy bodových nábojů nezávisela na postupu jejich sbližování). Potom
můžeme předpokládat například, že všechny vodiče nabíjíme od počátku současně,
přičemž rychlost nabíjení jednotlivých vodičů je úměrná konečnému náboji Qi , takže nabíjení bude i
současně ukončeno. Matematicky můžeme tuto situaci vyjádřit tak, že okamžité
potenciály a náboje jsou v každém okamžiku úměrny výsledným hodnotám:
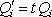 ,
,
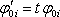 ,
kde t je bezrozměrný parametr 0 lb t lb l. Integrací pak najdeme
výslednou práci, resp. energii elektrostatického pole jako
,
kde t je bezrozměrný parametr 0 lb t lb l. Integrací pak najdeme
výslednou práci, resp. energii elektrostatického pole jako
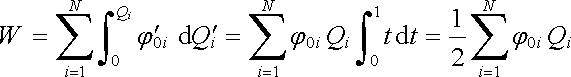 , , |
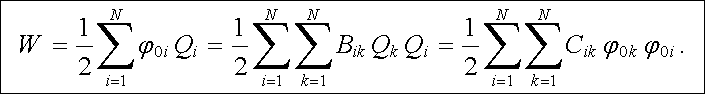 |
(1.209) |
Obecný výraz (1.209) můžeme použít k důkazu symetrie matice potenciálových, respektive influenčních koeficientů. Při nabíjení soustavy vodičů počněme tím, že nabijeme nejprve i-tý vodič nábojem Qi . Potom vykonáme práci
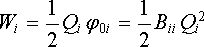 |
(1.210) |
(j0i představuje potenciál i-tého vodiče nabitého nábojem Qi v přítomnosti ostatních, a to nena-bitých vodičů). Potom nabíjíme k-tý vodič celkovým nábojem Qk . Tato práce bude rovna
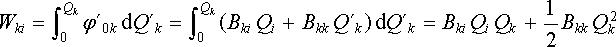 . . |
(1.211) |
Výsledná energie W = Wi + Wki nemůže záviset na pořadí, v němž vodiče nabíjíme, a musí být symetrická vůči záměně indexů i a k
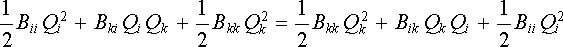 , , |
(1.212) |
odkud plyne rovnost Bik = Bki.
Z obecného výrazu (1.209) plyne jak výraz pro energii osamoceného vodiče (1.208) , tak výraz pro energii kondenzátoru. Uvážíme-li, že náboje na elektrodách kondenzátoru mají touž velikost a opačné znamení, a použijeme-li definice napětí kondenzátoru U = j01 - j02, dostáváme z (1.209) okamžitě
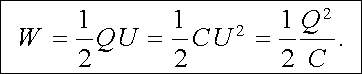 |
(1.213) |
Pro deskový kondenzátor s homogenním polem se snadno přesvědčíme, že tato energie je rovna energii elektrostatického pole v prostoru mezi deskami kondenzátoru (viz 1.2.8). Dosadíme-li do (1.213) výraz pro kapacitu deskového kondenzátoru (1.203) a nahradíme napětí U výrazem Ed, dostaneme po úpravě
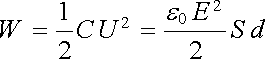 . . |
(1.214) |
První část součinu na pravé straně (1.214) e0 E2/2 představuje objemovou hustotu energie elektrostatického pole (1.91) , druhá část Sd je objem mezi deskami kondenzátoru. Podobný postup by bylo možné aplikovat i na obecnou soustavu vodičů. Energie soustavy nabitých vodičů je rovna energii elektro-statického pole v prostoru mezi vodiči (uvnitř vodičů je elektrostatické pole nulové).
Pro energii elektrostatického pole soustavy vodičů platí důležitá tzv. Thomsonova věta, jejíž důkaz lze najít například v [6]:
Náboje na soustavě pevných vodičů obklopených nevodivým prostředím jsou v rovnovážném stavu rozloženy po povrchu těchto vodičů vždy tak, aby energie výsledného elektrostatického pole byla minimální.
Průběh elektrostatického pole soustavy pevných vodičů je jednoznačně určen buď hodnotami jejich celkových nábojů, nebo hodnotami potenciálů. Představme si nyní, že vodiče změní poněkud svou polohu, přičemž zůstanou zachovány buď jejich celkové náboje, nebo hodnoty potenciálů. Náboje zůstanou zachovány na izolovaných vodičích; zachování potenciálů by bylo možné dosáhnout například tak, že připojíme vodiče ke zdrojům elektromotorického napětí, které budou měnit náboje vodičů tak, aby potenciál zůstal zachován. V tomto druhém případě není soustava vodičů z energetického hlediska izolována. Při změně polohy vodičů dojde ke změně potenciálových koeficientů, resp. kapacitních a influenčních koeficientů (které ve vakuu představují geometrické charakteristiky!), přerozdělí se náboje ve vodičích a vznikne nové elektrostatické pole s obecně novou hodnotou energie, která je při daných polohách vodičů minimální. Z tohoto hlediska je tedy energie elektrostatického pole soustavy vodičů jednoznačnou funkcí jejich polohy. Lze proto soudit, že pro určení rovnovážné polohy vodičů má význam potenciální energie. Je ovšem třeba mít na paměti, že v případě, kdy udržujeme na vodičích konstantní potenciály, dochází k výměně energie s okolím a energii elektrostatického pole nelze ztotožnit s potenciální energií izolované fyzikální soustavy.
Také pro nabité vodiče můžeme formulovat Earnshawovu větu (viz články 1.1.6 a 1.2.5), a to takto:
Nabité těleso nelze udržet v elektrostatickém poli ve stabilní rovnováze jen elektrickými silami.
Lze ukázat, že připojíme-li k soustavě nabitých vodičů další vodič, nelze jej umístit tak, aby jeho poloha a rozložení nábojů na vodičích odpovídala minimu energie soustavy (viz například [6]).
Podobně lze ukázat, že připojíme-li k soustavě nabitých vodičů nenabitý vodič, energie elektrostatického pole soustavy poklesne. Odpovídá to i známé skutečnosti, že na nenabitém vodiči dojde ve vnějším elektrostatickém poli k polarizaci nábojů a tento vodič bude k soustavě vodičů přitahován. Při jeho přibližování k soustavě konají tedy vnější síly zápornou práci a zmenšuje se celková energie.
Uvedené chování má své vyjádření i ve vlastnostech kapacitních a influ-enčních koeficientů (viz 1.4.5). Souvislost mezi změnou energie a změnami kapacitních a influenčních koeficientů budeme demonstrovat na příkladu dvou vodičů.
Máme-li nejdříve jeden izolovaný vodič nabitý nábojem Q, je jeho elektrostatická energie rovna
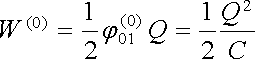 . . |
(1.215) |
Přiblížíme-li k němu další vodič, jenž je nenabitý, bude nová energie soustavy rovna
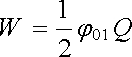 . . |
(1.216) |
Zde j01 představuje potenciál prvního vodiče v přítomnosti druhého vodiče, a to nenabitého . Z rovnic (1.199) pro dva vodiče, kde Q1 = Q, Q2 = 0, najdeme j01 a dosadíme do (1.216) . Máme
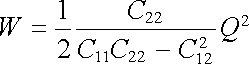 . . |
(1.217) |
Můžeme-li předpokládat W < W (0) , dostaneme srovnáním vztahů (1.215) a (1.217) nerovnost
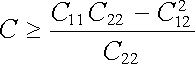 . . |
(1.218) |
V článku 1.3.2 jsme se zmiňovali o tom, že derivováním potenciální energie podle obecných souřadnic můžeme určit odpovídající složky působící síly. Podle toho, co bylo již uvedeno, má energie elektrostatického pole soustavy nabitých vodičů charakter potenciální energie, a umožňuje tedy vypočítat síly působící na vodiče v elektrickém poli.
Uvažme nejdříve situaci, kdy se na vodičích udržují konstantní náboje. Soustavu můžeme v tom případě považovat za energeticky izolovanou (práce se koná pouze na úkor energie pole). Je-li poloha vodiče udána šesti obecnými souřadnicemi xi, pak složky sil odpovídajících těmto souřadnicím najdeme jako
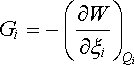 . . |
(1.219) |
Index Qi, u parciální derivace označuje, že derivování se provádí při konstantních nábojích.
Jsou-li naopak na
vodičích udržovány konstantní potenciály, je to možné pouze tak, že vodiče jsou
připojeny k vnějším zdrojům elektromotorického napětí, které zajišťují potřebné
změny náboje vodičů. Soustava není již energeticky izolovaná a není zcela
zřejmé, jak energie elektrostatického pole takové soustavy může sloužit k
výpočtu sil působících na vodiče. Označme změny nábojů na vodičích jako dQi , i = l ,..., N. Vnější zdroje přitom dodávají soustavě
energii
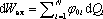 . Změní-li se poloha vodiče, bude změna
energie soustavy za předpokladu konstantních potenciálů podle
(1.209)
rovna
. Změní-li se poloha vodiče, bude změna
energie soustavy za předpokladu konstantních potenciálů podle
(1.209)
rovna
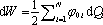 . Energie vnějších zdrojů se tedy změní
jednak na energii elektrostatického pole soustavy, jednak vykonává práci
spojenou se změnou polohy vodiče
. Energie vnějších zdrojů se tedy změní
jednak na energii elektrostatického pole soustavy, jednak vykonává práci
spojenou se změnou polohy vodiče
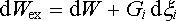 . . |
(1.220) |
Protože však dWex =2 dW, bude dW = Gi dxi a pro složky obecných sil dostaneme
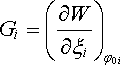 . . |
(1.221) |
Index j0i značí derivování při konstantních potenciálech. Všimněte si změny znaménka ve srovnání s výrazem (1.219) platným v izolované soustavě.
Chceme-li například určit sílu, která působí na elektrodu kondenzátoru, můžeme vyjít z výrazu pro jeho energii (1.213) . Předpokládejme přitom, že poloha elektrody je popsána souřadnicí x (například vzdáleností mezi deskami v případě deskového kondenzátoru) a kapacita C je funkcí této souřadnice C (x). Pak dostáváme při konstantních nábojích
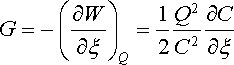 |
(1.222a) |
a při konstantním napětí
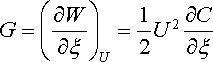 . . |
(1.222b) |
Oba výrazy jsou samozřejmě stejné. Je z nich vidět, že síla G má totéž znaménko jako derivace
kapacity a soustava má tedy tendenci svou kapacitu zvětšovat a energii
zmenšovat. V případě deskového kondenzátoru přitahují se jeho desky silou o
velikosti
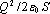 .
.
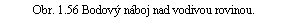

Všimněme si podrobněji vlastností jednoduché soustavy sestávající z nekonečné vodivé roviny a bodového elektrického náboje Q > 0 ve vzdálenosti h od této roviny. Vodivá rovina nechť je uzemněna, a tedy na nulovém potenciálu. Počátek kartézské soustavy souřadnic můžeme umístit do paty kolmice spuštěné z bodu Q na rovinu a osu z vést nábojem Q (viz obr. 1.56). Máme určit elektrostatické pole této soustavy v poloprostoru, kde leží náboj Q, rozložení indukovaného náboje na vodivé rovině, sílu, kterou je bodový náboj k rovině přitahován, a energii této soustavy.
Víme již, že jde o zvláštní případ základní úlohy elektrostatiky, která vyžaduje řešit Laplaceovu rovnici Dj = 0 s okrajovou podmínkou j = 0 ve všech bodech roviny. Pomocí metody elektrostatického zobrazení můžeme splnit okrajovou podmínku tak, že umístíme náboj -Q zrcadlově souměrně k rovině a budeme vyšetřovat pole této dvojice bodových nábojů. Víme, že jde o pole konečného elektrického dipólu. Průběh siločar v rovině vedené osou z je kvalitativně znázorněn na obr. 1.57.

Obr. 1.57 K metodě elektrostatického zobrazení.
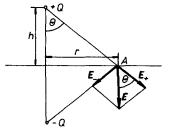
Na vzdálenostech značně převyšujících výšku h lze pole přibližně popsat polem bodového dipólu umístěného v počátku (1.125) , kde p = 2hQ . Dále můžeme snadno určit intenzitu elektrostatického pole na vodivé rovině (obr. 1.58). Vektor intenzity je k rovině kolmý a má velikost
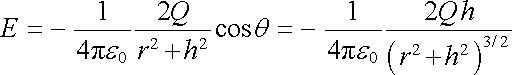 . . |
(1.223) |
Pro r >> h souhlasí tento výraz s (1.127) . Plošnou hustotu náboje na vodivé rovině najdeme pomocí Coulombovy věty jako
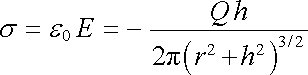 . . |
(1.224) |
Integrací v polárních souřadnicích po celé rovině se snadno přesvědčíme, že celkový indukovaný náboj je roven právě - Q:
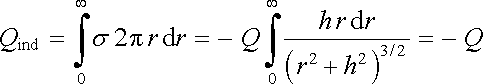 . . |
(1.225) |
Konečně určíme složku síly, kterou je náboj Q k rovině přitahován a energii soustavy
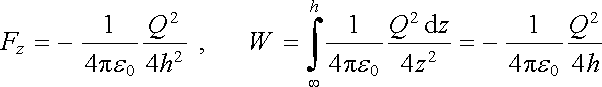 . . |
(1.226) |
Znaménko minus u složky síly vyjadřuje, že jde o sílu přitažlivou.Všimněte si, že energie soustavy není totožná s interakční energií dvojice bodových nábojů Q a -Q ve vzdálenosti 2h. Proč?
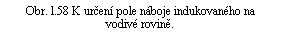
Metodou elektrostatického zobrazení lze řešit například i úlohu s okrajovou podmínkou j = 0 na zadané uzemněné kulové ploše poloměru R. Střed této kulové plochy umístíme do počátku souřadnic. Dále mějme bodový náboj Q1 na ose x v bodě x1 > R (obr. 1.59). Máme najít elektrostatické pole v celém prostoru vně kulové plochy.

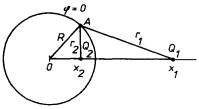
Opět se pokusíme nahradit okrajovou podmínku umístěním fiktivního bodového náboje Q2 na ose x ve vzdálenosti x2 < R, tj. uvnitř kulové plochy. V libovolném bodě na kulové ploše musí platit
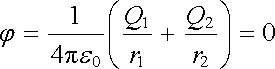 , , |
odkud
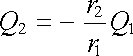 . . |
Poměr r2 / r1 musí být zachován konstantní pro všechny body na kulové ploše. Toho lze dosáhnout volbou vzdálenosti x2 tak, aby platilo
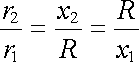 , , |
neboli aby vzdálenosti x1, x2
splňovaly podmínku kulové inverze
 . Musíme tedy zvolit
. Musíme tedy zvolit
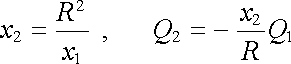 |
(1.227) |
a studovat pole této dvojice bodových nábojů.
Sílu, kterou bude náboj Q1 ke kouli přitahován, určíme jako
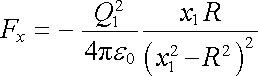 . . |
(1.228) |
Energie soustavy bude rovna záporné práci, kterou jsme vykonávali při přibližování náboje Q1 z nekonečna k uzemněné kouli:
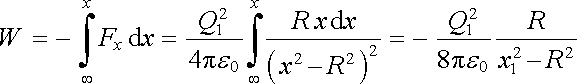 . . |
(1.229) |
Pokud bude vodivá koule izolovaná a nikoli uzemněná, bude na jejím povrchu konstantní, obecně nenulový, potenciál a nulový celkový indukovaný náboj. Abychom tuto situaci vystihli, musíme do středu koule umístit další fiktivní náboj rovný právě -Q2. Snadno ověříme, že náboj Q1 bude tentokrát ke kouli přitahován silou
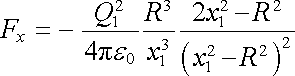 |
(1.230) |
a soustava bude mít energii
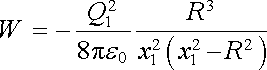 . . |
(1.231) |
Metodu elektrostatického zobrazení použijeme ještě k určení elektrostatického pole v okolí vodivé koule o poloměru R, vložené do vnějšího homogenního pole E0 (o pole uvnitř koule se opět nemusíme zajímat, neboť víme, že je nulové).
Po vložení do vnějšího pole vzniknou na povrchu koule indukované náboje, jejichž pole se bude superponovat s polem E0. Povrch koule přitom zůstane ekvipotenciální plochou a výsledné pole bude osově symetrické s osou symetrie procházející středem koule ve směru pole E0.
Úloha jak nalézt výsledné pole bude zřejmě vyřešena, podaří-li se nám najít soustavu bodových nábojů, která po vložení do homogenního pole bude mít ku-lovou ekvipotenciální plochu o poloměru R. Ukážeme, že takovou soustavou je bodový elektrický dipól s dipólovým momentem p orientovaným ve směru E0.
Umístíme-li dipól do počátku soustavy souřadnic, jejíž osa z má směr p i E0, můžeme potenciál výsledného pole j (r) vybrat ve tvaru
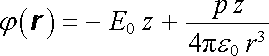 . . |
Zvolíme-li velikost indukovaného dipólového momentu
p = 4pe0 R3 E0 , (1.232)
budeme mít
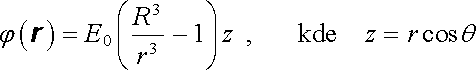 . . |
Odtud je zřejmé, že při r = R bude potenciál na kulové ploše konstantní, a to nulový. Vodivá koule se tedy v homogenním poli zpolarizuje a chová se jako dipól o momentu (1.232) .
Na jejím povrchu musí platit hraniční podmínky pro normálové a tečné složky intenzity elektrického pole. Složky pole ve směru x a z tam jsou ve tvaru
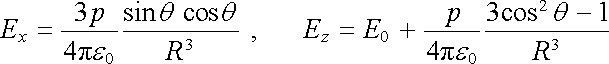 . . |
Normálové a tečné složky dostaneme jako Ea = Ex sin q + Ez cosq , Et = -Ex cosq + Ez sinq a hraniční podmínky nám dávají
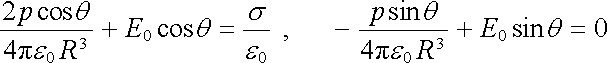 . . |
Druhá podmínka vyjadřuje opět vztah (1.232) , z první podmínky můžeme určit rozložení hustoty indukovaného povrchového náboje:
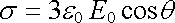 . . |
(1.233) |
Vidíme znovu, že kulová plocha s takto rozloženým povrchovým nábojem se chová navenek jako dipól (viz 1.3.5d). Celkový náboj indukovaný na každé z polokoulí je zřejmě Q = 3pe0E0R2 a jeho těžiště je ve vzdálenosti 2R/3 od středu koule.
Určeme kapacitu soustavy dvou koncentrických dutých vodivých koulí o poloměrech R1 < R2 . Je-li vnitřní koule nabita nábojem Q, bude pole mezi nimi dáno vztahem (1.104) , jehož integrací dostáváme
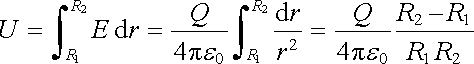 . . |
Kapacita takové soustavy vodičů je tedy
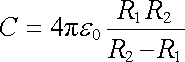 . . |
(1.234) |
Všimněme si, že při R2 - R1 << R2 můžeme považovat pole mezi oběma kulovými plochami za lokálně homogenní a výraz pro kapacitu (1.234) přechází ve výraz pro kapacitu deskového kondenzátoru.
Určíme kapacitu soustavy dvou dlouhých koaxiálních vodivých válců délky l o poloměrech R1 < R2. Vnitřní válec je nabit nábojem Q a pro napětí mezi válci dostáváme podle (1.110)
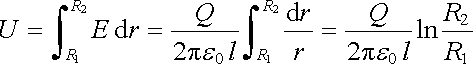 . . |
Tedy
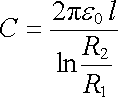 |
(1.235) |
a kapacita připadající na jednotku délky koaxiálního vodiče je
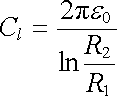 . . |
(1.236) |
Mějme dva přímé nabité rovnoběžné vodiče (dráty) konečného průřezu (polo-měru R) ve vzájemné vzdálenosti l >> R s lineárními hustotami náboje t > 0, -t.
Díky této volbě náboje je vyšetřovaná soustava v jistém smyslu analogická s kondenzátorem a můžeme určit kapacitu délkové jednotky takového vedení (viz obr. 1.60).

Elektrické pole v bodě A mezi vodiči ve vzdálenosti r od osy prvního vodiče najdeme superpozicí polí dvou lineárních nábojů jako
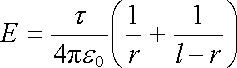 . . |
Pro napětí pak obdržíme vztah
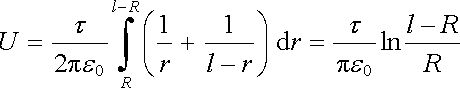 , , |
odkud dostaneme pro kapacitu na jednotku délky
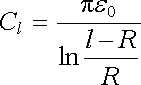 . . |
(1.237) |
Při integrování napětí v mezích od R do l - R bylo podstatné, že vodiče jsou konečného průřezu. Kdybychom chtěli počítat napětí pro idealizované, nekonečně tenké vodiče, dostali bychom divergující integrál.
Elektrostatické pole působící na náboje rozložené na povrchu vodičů vyvolává v těchto vodičích silové účinky. Díky tomu, že intenzita elektrostatického pole je vždy kolmá k povrchu vodiče, mohou být tyto silové účinky popsány povrchovým napětím fE, které vyjadřuje sílu působící na jednotku plochy vodiče ve směru normály.
Intenzita pole E při povrchu vodiče je s povrchovou hustotou náboje s v daném místě vázána Coulombovou větou E = s/e0. Pro výpočet síly DFE působící na malou část povrchu DS však musíme z celkové intenzity E vyloučit vlastní příspěvek náboje s DS na uvažované plošce. Pomocí Gaussova zákona se snadno přesvědčíme, že tento příspěvek činí právě polovinu celkové intenzity E. Intenzita Ec buzená ostatními povrchovými náboji má tedy hodnotu Ec = s/2e0 a pro sílu DFE dostáváme
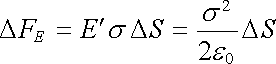 . . |
Povrchové napětí
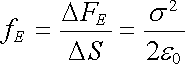 |
můžeme užitím Coulombovy věty vyjádřit pomocí celkové intenzity pole E u povrchu vodiče
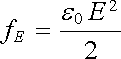 . . |
(1.238) |
Síla působící na povrch vodiče ze strany elektrostatického pole je vyrovnávána pružnými silami mechanického napětí v tělese.
Veličina fE je podle (1.238) rovna objemové hustotě energie elektrostatického pole (1.91) . Tuto souvislost si můžeme ozřejmit následujícím způsobem. Uvažme povrchově nabitou kouli poloměru R. Stlačíme-li tuto kouli na poloměr R - DR, vykonáme práci proti silám povrchového napětí
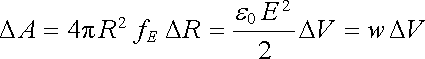 . . |
Po stlačení koule se objeví elektrostatické pole v objemu kulové slupky DV = 4pR2DR, kde byla dříve intenzita pole nulová. Vykonaná práce se pak rovná energii elektrostatického pole v tomto objemu.
Síly působící mezi nabitými vodiči mohou být využity k měření napětí. Přístroje založené na tomto principu se nazývají elektrostatické měřicí přístroje a jsou vždy uzpůsobeny tak, aby bylo možné srovnávat silové účinky elektrostatického pole se silami jiného druhu (gravitačními, elastickými či jinými). Podle způsobu konstrukce a použití rozeznáváme elektroskopy, určené především pro demonstrační účely, a dále elektrometry a elektrostatické voltmetry. První z nich jsou určeny pro měření malých napětí. Elektrostatické voltmetry mívají naopak robustnější konstrukci a jsou určeny pro měření napětí desítek až tisíců voltů. Historicky významné jsou tzv. Thomsonovy váhy, jejichž princip spočívá ve srovnání elektrostatické síly mezi elektrodami deskového kondenzátoru pomocí závaží a které představují absolutní měřidlo napětí.
Konkrétním popisem konstrukce elektrostatických měřicích přístrojů se nebudeme zabývat; v této otázce odkazujeme na učebnici [5], v níž jsou rovněž uvedeny citace na další, speciálnější prameny. Všimneme si pouze obecných zákonitostí, určujících "průběh stupnice" elektrostatických přístrojů, které jsou dány vlastnostmi sil působících na vodiče v elektrostatickém poli, a jsou tudíž pro všechny elektrostatické přístroje společné.
Měřicí systém elektrostatického přístroje je vždy tvořen soustavou několika elektrod, z nichž alespoň jedna je pohyblivá. Její uložení je takové, aby jí umožňovalo konat definovaný pohyb popsaný jedinou vhodnou souřadnicí g. Klidová poloha této elektrody g0 je dále jednoznačně vymezena jejím spojením s elasticky snadno deformovatelnými prvky (torzní vlákno, pružina apod.), které vytváří tzv. direkční síly. Přivedeme-li na elektrody přístroje napětí které chceme měřit, vychýlí se pohyblivé elektrody účinkem elektrostatické síly ze své klidové polohy. Tím se však deformují zmíněné elastické prvky a vzniklé direkční síly se snaží vrátit elektrody do výchozí polohy. Nový klidový stav je dán rovnováhou mezi elektrostatickými a direkčními silami a příslušná změna souřadnice g - g0 je mírou měřeného napětí.
Jednotlivé elektrody měřicího systému jsou ve většině případů propojeny tak, že tvoří kondenzátor ke kterému se připojuje měřené napětí, přičemž měrná pohyblivá elektroda je součástí jedné elektrody kondenzátoru. Jeho kapacita C je tedy funkcí souřadnice g; C = C(g). Je-li na svorky přístroje přivedeno konstantní napětí U, je zobecněná elektrostatická síla GE, vychylující měrnou elektrodu, dána vztahem (1.222) a platí pro ni tedy
(eq0327).
O direkční síle, která je elastické povahy, můžeme předpokládat, že je úměrná výchylce s danou konstantou úměrnosti KD : GD = -KD(g - g0). Podmínka rovnováhy bude mít tedy tvar
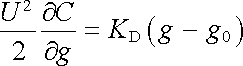 |
a pro výchylku přístroje (g - g0) z ní dostaneme
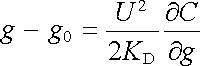 . . |
(1.239) |
Ze vztahu (1.239) vyplývá, že průběh stupnice přístroje je určen závislostí C(g). Bude-li například kapacita C lineární funkcí souřadnice g, bude výchylka úměrná čtverci napětí a průběh stupnice bude kvadratický. Vzhledem k tomu, že pro každý přístroj je žádoucí lineární průběh stupnice, pokusíme se najít odpovídající tvar funkce C(g). Dosadíme-li požadovanou závislost g - g0 = KU do (1.239) , dostaneme podmínku
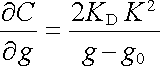 |
a z ní požadovaný tvar funkce
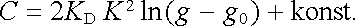 |
(1.240) |
Přístroj bude mít tedy lineární stupnici, jestliže kapacita C bude logaritmickou funkcí souřadnice (g - g0) . Je zřejmé, že v oboru malých výchylek nelze této podmínce z principiálních důvodů vyhovět žádnou realizovatelnou konstrukcí, neboť při g - g0 by kapacita musela vzrůstat do nekonečna jako funkce l/(g - g0). Stupnice každého elektrostatického přístroje je tedy v okolí počátku zhuštěna. To znamená, že citlivost přístroje s klesajícím napětím klesá, což přináší obtíže při měření malých napětí.