V úvodu oddílu 1.4 o elektrostatickém poli vodičů jsme roztřídili látky na vodiče, které mají schopnost převádět elektrický náboj, a nevodiče, dielektrika, která tuto schopnost nemají a mohou sloužit jako izolanty. To však neznamená, že by se dielektrikum a vnější elektrostatické pole vzájemně nijak neovlivňovaly.
O charakteru tohoto vlivu se můžeme přesvědčit jednoduchým experimentem. Vezměme například deskový kondenzátor, jehož vlastnosti jsme studovali v článku 1.4.5 a zaplňme prostor mezi jeho elektrodami homogenním izotropním dielektrikem. Experimentálně zjistíme, že při zachování náboje na elektrodách napětí mezi elektrodami po vložení dielektrika poklesne z původní hodnoty U0 na jistou hodnotu U a kapacita naopak vzroste z původní hodnoty C0 na hodnotu C. Označíme-li U0/U = er bude podle (1.201) platit
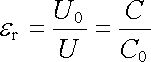 . . |
(1.241) |
Bezrozměrná veličina er se nazývá relativní permitivitou daného dielektrika. Jak uvidíme v článku 1.5.4, je to parametr látky, který v určité aproximaci charakterizuje z makroskopického hlediska chování dielektrika v elektrostatickém poli. V kapitole 7 budou podrobněji studovány jeho vlastnosti, a to i z hlediska mikroskopické struktury látek. Uvidíme, že pro různá dielektrika může být značně rozdílný: od hodnot jen nepatrně větších než jedna až po hodnoty řádu 104 v případě tzv. feroelektrik.
Nabitý deskový kondenzátor, jehož prostor mezi elektrodami je zcela vyplněn dielektrikem, přináší novou, fyzikálně velmi závažnou otázku o charakteru elektrického pole v prostoru mezi elektrodami. Speciálně vzniká otázka, má-li fyzikální smysl hovořit o elektrostatickém poli v látkovém prostředí.
Již v článku 1.2.1 bylo zdůrazněno, že elektrostatické pole vůbec (tj. i elektrostatické pole ve vakuu) má přesně vzato smysl jen jako pole makroskopické, přičemž intenzitu pole E je nutné chápat jako výslednou střední hodnotu polí vytvořených jednotlivými nositeli náboje. V případě pole v dielektriku se navíc superponuje střední hodnota polí vytvořených náboji dielektrika v bezprostřední blízkosti vyšetřovaného bodu. Vlastnosti tohoto výsledného pole budou zkoumány v následujících článcích tohoto oddílu.
I když je v této kapitole naším úkolem budovat fenomenologický popis založený na experimentálních poznatcích makroskopického charakteru, je užitečné podat stručnou, alespoň kvalitativní charakteristiku situace z mikroskopického hlediska. Víme, že látka má atomární, přetržitou strukturu a že součástí atomů a molekul jsou elektricky nabité částice - protony a elektrony. Z mikroskopického hlediska představuje tedy dielektrikum velmi složitou soustavu elektrických nábojů, které jsou navíc v neustálém pohybu. V jednom krychlovém centimetru pevné či kapalné látky se nachází 1020-1022 molekul, popř. atomů, vzá-jemně vzdálených 10-7-10-8 cm. Fyzikální studium vlastností atomů a molekul vychází přitom za rámec klasické fyziky, neboť pohyby a vlastnosti těchto částic se řídí zákony fyziky kvantové. Zákony kvantové fyziky je nutné respektovat především v případě velké koncentrace částic, jakou nacházíme u pevných a kapalných látek a v případě teplot blízkých absolutní nule.
Při makroskopickém popisu můžeme využít skutečnost, že atomy či molekuly jsou elektricky neutrální soustavy mikroskopických nábojů. Víme, že elektrostatické pole takové soustavy můžeme na vzdálenostech značně převyšujících její rozměry vyjádřit jako pole multipólových momentů různých řádů (článek 1.3.2). V prvním nenulovém přiblížení se tedy uplatní elektrický dipólový moment atomu či molekuly a jejich pole se bude jevit v dostatečné vzdálenosti jako pole bodového elektrického dipólu.
Vzniká samozřejmě otázka, zda atomy a molekuly mají vždy vlastní nenulový elektrický dipólový moment. Zde záleží na vlastnostech konkrétního látkového prostředí, daného atomu či molekuly. Dielektrika, jejichž molekuly mají náboje rozloženy takovým způsobem, že jako celek vykazují vlastní elektrický dipólový moment, patří ke skupině látek, které nazýváme polárními dielektriky. (Typickým příkladem polární molekuly je molekula vody, jejíž vlastní elektrický dipólový moment má velikost 6,1 . 10-30 coulomb metr, k dalším náleží kyselina chlorovodíková, amoniak, některé organické molekuly a jiné.)
Při vložení polárního dielektrika do vnějšího elektrostatického pole se elektrické dipólové momenty budou natáčet vlivem silového momentu pole do směru siločar a makroskopický, jednotkový objem látky můžeme pak charakterizovat celkovým dipólovým momentem. Protože tato polarizace vzniká v důsledku orientace pevných dipólových momentů, nazýváme ji polarizací orientační. Je zřejmé, že tato polarizace nebude nikdy úplná; chaotický tepelný pohyb molekul působí, že dipólové momenty se budou více nebo méně odchylovat od směru vnějšího elektrického pole.
Další důležitou okolností je to, že se atomy a molekuly nechovají jako tuhá tělesa, nýbrž podléhají deformaci. Ve vnějším elektrickém poli budou na náboje tvořící atomy a molekuly působit síly, které způsobují prostorové rozdělení těchto nábojů, a tedy vznik indukovaných elektrických dipólových momentů. Tyto indukované momenty jsou však ve srovnání s vlastními dipólovými momenty o několik řádů slabší ( ~ 10-35 coulomb metr); atomy a molekuly se významně deformují až ve velmi silných elektrických polích. Dielektrika, jejichž atomy (molekuly) nemají vlastní elektrické dipólové momenty, získávají ve vnějším poli tedy jen momenty indukované, orientované rovněž ve směru siločar pole. Jde o látky, které nazýváme nepolárními dielektriky.
Uvedené představy, které budeme v kapitole 7 dále konkretizovat, platí ovšem pouze přibližně. Polarizace polárního dielektrika nebývá například nikdy pouze orientační, i zde se může uplatnit vliv indukovaných momentů. V ojedinělých případech dochází v dielektriku k ionizaci, kdy molekula či atom získává nenulový elektrický náboj, a jeho pole je pak významnější než pole elektrického dipólu. Kromě toho víme, že dipólové přiblížení popisuje elektrické chování atomů a molekul pouze s přesností na opravu vyvolanou polem vyšších multipólových momentů. Přesto však můžeme makroskopické chování dielektrika v elektrickém poli s dobrou přesností popsat na základě jednoduchého modelu spojitého, bezstrukturního, rozložení elektrických dipólů.
Na základě výsledků předchozího článku, které jsou v plném souhlasu s expe-rimentální zkušeností, je možné stav daného objemu dielektrické látky charakterizovat výsledným elektrickým dipólovým momentem, který může být chápán jako střední hodnota vektorové sumy dipólových momentů jednotlivých atomů či molekul. Aplikujeme-li uvedený model spojitého objemového rozložení elektrických dipólů, můžeme stav dielektrika popsat pomocí výsledků uvedených v článku 1.3.4, ve kterém byly studovány vlastnosti abstraktního objemového rozložení dipólových momentů.
Jak jsme viděli, jedinou charakteristikou uvedeného modelu je vektor elektrické polarizace P(r ), který má význam objemové hustoty dipólového momentu v daném bodě r. Experimentálně pozorovaný výsledný dipólový moment pV libovolného objemu V studovaného dielektrika pak lze vyjádřit vztahem
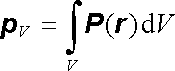 , , |
(1.242) |
který může být považován za (implicitní) definici vektoru polarizace.
Elektrostatické pole vytvořené konečným objemem V spojitě rozložených elektrických dipólů je ekvivalentní elektrostatickému poli makroskopických nábojů rozložených na povrchu tohoto objemu s plošnou hustotou sp(r) a uvnitř tohoto objemu s objemovou hustotou rp(r). Plošná hustota sp závisí přitom pouze na průběhu vektoru elektrické polarizace P a směru jednotkového vektoru normály n na povrchu objemu, objemová hustota rp je různá od nulové pouze v případě nehomogenní polarizace. Platí obdoba rovnic (1.168)
 . . |
Vztahy (1.168) byly odvozeny v článku 1.3.4. Lze je však získat i elementárním (i když méně rigorózním) postupem. Mysleme si malý objem DV těsně přimykající k danému místu povrchu, a to tak, že na povrchu vyčleňuje plošku DS. Výšku objemu DV volíme tak, aby v něm ležela jen jedna vrstva elementárních dipólů. Předpokládáme, že tyto dipóly jsou orientovány vzájemně souhlasně, rovnoběžně a obecně pod úhlem a k vektoru normály (obr. 1.61). Jsou-li p = Ql elementární dipólové momenty, dostaneme pro výsledný dipólový moment objemu DV výraz pDV = PDV = PDS l cosa = P(n.l ) DS = (P.n) DSl. Zároveň platí pDV = sp DSl, odkud plyne, že
sp = P.n .
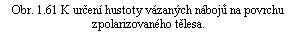
Uvažme nyní
uzavřenou plochu S ležící uvnitř
objemu V. Potom tok vektoru P touto plochou
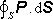 představuje celkový náboj, který při
zpolarizování dielektrika plochou S
vytekl. (Pro spojité homogenní rozložení dipólů bude tento náboj jistě nulový.)
Musí se tedy rovnat úbytku vázaného objemového náboje
představuje celkový náboj, který při
zpolarizování dielektrika plochou S
vytekl. (Pro spojité homogenní rozložení dipólů bude tento náboj jistě nulový.)
Musí se tedy rovnat úbytku vázaného objemového náboje
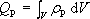 v objemu V
a použitím Gaussovy věty snadno nahlédneme, že
v objemu V
a použitím Gaussovy věty snadno nahlédneme, že
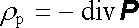 . . |
Velmi důležitou je otázka, zda se polarizační náboje v dielektriku popsané hustotami rp a sp nějak liší od dosud zkoumaných nábojů, například na povrchu vodičů. Polarizační náboje se na rozdíl od nábojů ve vodičích nemohou v dielektriku přemisťovat na makroskopické vzdálenosti a nazýváme je proto vázanými náboji. Existence makroskopických vázaných nábojů ve zpola-rizovaném dielektriku je však fyzikálně reálná a může být experimentálně pro-kázána. Mechanismus jejich vzniku byl demonstrován názorně v příkladu 1.3.5c (viz obrázky 1.39 a 1.40).
Obecně vzato mohou v dielektriku existovat i náboje volné vznikající při zelektrizování dielektrika různým způsobem. Potom budeme rozlišovat celkovou objemovou hustotu makroskopických nábojů rc, objemovou hustotu nábojů volných r a objemovou hustotu nábojů vázaných rp:
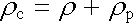 . . |
(1.243) |
Pokud jde o náboje vázané, vzniklé zpolarizováním dielektrika, je zřejmé, že jejich úhrnný náboj je vždy roven nule a jejich rozložení v tělese je určeno přítomností vnějšího elektrostatického pole nebo sil jiné fyzikální povahy.
Elektrostatické pole v přítomnosti dielektrik můžeme tedy určit jako pole makroskopických elektrických nábojů, a to jednak volných, jednak vázaných. Je ovšem možné se ptát, zda intenzita elektrostatického pole vytvářená těmito dvěma druhy elektrických nábojů je téže fyzikální povahy a zda je možné tato dvě pole superponovat, abychom dostali výslednou sílu působící na bodový elektrický náboj v daném bodě prostoru. Již v oddílu 1.4, když jsme vyšetřovali chování vodičů v elektrostatickém poli, jsme zdůrazňovali, že v objemu vodiče se ustaví nulová hodnota intenzity elektrostatického pole působícího na makroskopické náboje, tedy pole určitým způsobem vystředovaného. Neznamená to samozřejmě, že by v objemu vodiče přestaly existovat mikroskopické náboje, například uvnitř atomů a molekul, že by neexistovala prostorově i časově proměnná lokální, mikroskopická pole, dokonce značných intenzit.
Při makroskopickém popisu, který máme na mysli v této kapitole, se však zajímáme pouze o střední hodnoty intenzity elektrostatického pole v látkovém prostředí, které také můžeme experimentálně přímo pozorovat a měřit. To se vztahuje i na elektrostatické pole vázaných nábojů v dielektriku. Jakožto střední, makroskopická pole můžeme pak pole volných i vázaných nábojů superponovat a zavést výslednou intenzitu elektrostatického pole
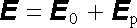 . . |
(1.244) |
Vektor E0 značí intenzitu pole volných nábojů, Ep vázaných.
Nyní budeme studovat obecné vlastnosti elektrostatického pole v přítomnosti dielektrika. Pro dielektrikum zvolíme přitom idealizovaný model spojitého prostředí, jehož elektrické vlastnosti jsou plně popsány zadáním vektoru polarizace P(r). Tento vektor souvisí s koncentrací objemových a plošných vázaných nábojů vztahy (1.168) . Makroskopické hodnoty intenzity elektrostatického pole volných a vázaných nábojů budeme přitom superponovat (srov. (1.244) ).
Především je zřejmé, že i v přítomnosti vázaných statických nábojů musí zůstat elektrostatické pole potenciálním, a bude tedy platit (1.62) , respektive (1.63)
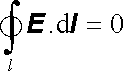 , , |
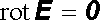 . . |
Dále zůstane v platnosti Gaussův zákon pro libovolnou uzavřenou plochu S. Přitom musíme vzít v úvahu celkový elektrický náboj, volný i vázaný, uvnitř Gaussovy plochy. Máme tedy
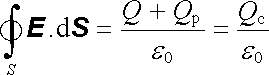 . . |
(1.245) |
Předpokládáme-li že uvnitř plochy S jsou pouze objemově rozložené vázané náboje, dostaneme s ohledem na (1.168)
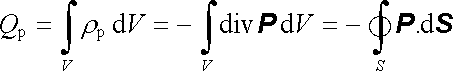 , , |
a tedy
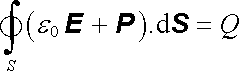 . . |
Poslední vztah se zjednoduší, zavedeme-li nový vektor
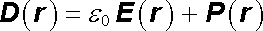 |
(1.246) |
nazývaný vektorem elektrické indukce. S jeho pomocí můžeme zapsat Gaussův zákon ve tvaru, v němž explicitně vystupují pouze volné náboje
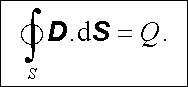 |
(1.247) |
Předpokládáme-li, že uvnitř plochy S nejsou ani volné plošné náboje, můžeme známým způsobem používajícím Gaussovy věty vektorové analýzy přejít k diferenciálnímu tvaru rovnice (1.247)
(eq0347)(l.248)
kde veličina r představuje objemovou hustotu volných nábojů
Vyšetřme nyní vlastnosti vektoru elektrické indukce v okolí plošných nábojů. Nechť jsou na ploše S rozloženy volné i vázané náboje s hustotami s a sp. Nechť je prostor na jedné straně plochy vyplněn dielektrikem 1 o polarizaci P1, prostor na druhé straně plochy dielektrikem 2 o polarizaci P2.
Zapíšeme-li vztah (1.80) ve vektorovém tvaru, dostaneme pro sumární plošnou hustotu náboje
(eq0348),(l.249)
kde n1 je jednotkový vektor normály směrující do oblasti 1.
Můžeme
předpokládat, že celková hustota vázaných nábojů je rovna součtu hustot
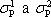 , z nichž první je dána polarizací
samotného dielektrika 1 a druhá polarizací samotného dielektrika 2 podle vztahu
(1.168)
Potom platí
, z nichž první je dána polarizací
samotného dielektrika 1 a druhá polarizací samotného dielektrika 2 podle vztahu
(1.168)
Potom platí
(eq0350)(l.250)
a po dosazení do (l 249) dostaneme
(eq0351),(l.251)
neboli podle (1.246)
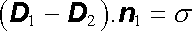 . . |
(1.252) |
Nespojitost normálových složek vektoru elektrické indukce je dána pouze plošnou hustotou volných nábojů. Při průchodu plochou, na níž jsou pouze vázané plošné náboje, zůstávají normálové složky vektoru elektrické indukce spojité.
Pro elektrostatické pole v dielektriku můžeme tedy zapsat obecné rovnice, v nichž vystupují pouze objemové, resp. plošné hustoty volných nábojů. Pro objemové volné náboje[9] máme tedy
(eq0353)(l.253)
pro plošné volné náboje
 |
(1.254) |
Vektor elektrické indukce byl zaveden formálně vztahem (1.246) jako vektorový součet vektoru polarizace a veličiny e0 E. Jeho význam spočívá v tom, že zavedením vektoru elektrické indukce k popisu elektrického pole v dielektriku můžeme vyloučit z explicitních úvah vázané náboje. Pro bezprostřední vyjádření fyzikálních účinků elektrostatického pole zůstává ovšem i v dielektrickém prostředí rozhodující veličinou intenzita pole. Principiálně by bylo možné budovat teorii elektrostatického pole bez zavedení vektoru elektrické indukce. Při řešení úloh se zadaným rozložením volných nábojů v dielektriku je však tato veličina užitečná.
Jak bylo ukázáno v předchozím článku, je elektrostatické pole za přítomnosti dielektrik úplně popsáno dvěma vektorovými funkcemi E(r) a D(r). Tyto veličiny vyhovují integrálním podmínkám (1.62) a (1.247) , které mohou být nahrazeny diferenciálními rovnicemi (1.253) , doplněnými podmínkami (1.254) pro plochy nesoucí plošné náboje. Za zdroj elektrostatického pole můžeme obvykle považovat volné náboje, jejichž rozložení v prostoru známe. Uvedený popis, například rovnice (1.253) , by měl pak umožňovat nalézt oba vektory E i D, je však nedostatečný pro určení šesti neznámých funkcí Ex, Ey, Ez, Dx, Dy, Dz. Uvedená soustava rovnic, která platí zcela obecně a přesně popisuje vlastnosti elektrostatického pole, musí být proto doplněna dalším vztahem mezi vektorem elektrické indukce D a intenzitou pole E. Takový vztah je již závislý na konkrétních vlastnostech daného dielektrika a vyplývá z definice vektoru elektrické indukce (1.246) , je-li udána souvislost vektorového pole P(r) s intenzitou E(r) v dielektriku. Nazývá se proto materiálovým vztahem.
Problematika materiálových vztahů může být značně komplikovaná a nemůže být v podstatě řešena zcela obecně. V kapitole 7 podrobněji uvidíme, že vztah mezi polarizací a intenzitou pole může záviset na značném počtu faktorů a nemusí být ani dán jednoznačnou funkcí. Je proto vždy zapotřebí vytvořit vhodný model daného dielektrika a materiálový vztah odpovídajícím způsobem aproximovat.
Pro obecné úvahy se často vystačí s velmi hrubou aproximací materiálových vztahů. V prvním přiblížení je možné vlastnosti reálných dielektrik aproximovat dvěma abstraktními typy dielektrických látek, vystihujícími extrémní situace. Jsou to pojmy ideálně tvrdého a ideálně měkkého dielektrika.
V případě ideálně tvrdého dielektrika předpokládáme určitou permanentní polarizaci P0(r) v daném bodě, která již na hodnotě intenzity pole nezávisí.
V případě ideálně měkkého dielektrika předpokládáme lineární závislost vektoru polarizace P v daném bodě na výsledné intenzitě pole E v tomto bodě. Pro izotropní a homogenní prostředí je možné tuto závislost zapsat ve tvaru
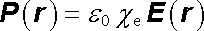 . . |
(1.255) |
Bezrozměrná veličina ce charakterizuje vlastnosti dielektrika a nazývá se jeho elektrickou susceptibilitou (něco jako "vnímavostí"). Je to vždy kladná veličina, která však pro různé materiály může nabývat značně rozmanitých hodnot. V kapitole 7 poznáme některé její konkrétní vlastnosti pro důležité typy dielektrik. Použitím definičního vztahu (1.246) snadno nalezneme vztah mezi elektrickou indukcí a intenzitou pole v měkkém dielektriku. Platí
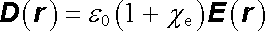 . . |
(1.256) |
Vraťme se nyní k úloze diskutované v úvodu článku 1.5.1 a vypočítejme, jak se změní napětí na elektrodách deskového kondenzátoru, zaplníme-li prostor mezi nimi ideálně měkkým izotropním dielektrikem o susceptibilitě ce. Aplikací Gaussova zákona pro elektrickou indukci (1.247) snadno zjistíme, že mezi elektrodami je homogenní pole, jehož elektrická indukce je dána plošnou hustotou volného náboje na elektrodách s, D = s. V případě prázdného kondenzátoru platí pro intenzitu pole mezi elektrodami vztah (1.99) , E0 = s/e0. Odtud pro napětí na elektrodách prázdného kondenzátoru dostáváme U0 = E0 d = s d/e0 (viz obr. 1.62). Pro napětí kondenzátoru s dielektrikem pak podle (1.256) dostáváme
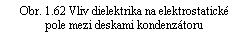
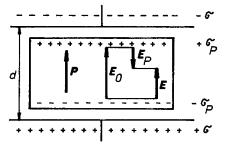
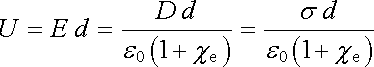 , , |
odkud plyne
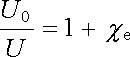 . . |
(1.257) |
Podle (1.241) tedy máme vztah mezi dříve zavedenou relativní permitivitou er a susceptibilitou ce
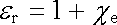 . . |
(1.258) |
Z provedených úvah současně vidíme, že výsledek zmíněného experimentu (1.241) bude nezávislý na velikosti náboje na kondenzátoru jedině tehdy, bude-li mít použitý materiál vlastnosti ideálně měkkého lineárního dielektrika.
Použitím (1.258) můžeme vztah (1.256) přepsat na tvar
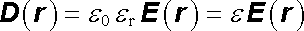 . . |
(1.259) |
Veličina
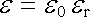 , , |
(1.260) |
která má rozměr permitivity vakua (tj. farad na metr), se nazývá permitivitou daného dielektrika.
Je-li dielektrikum nehomogenní, je permitivita funkcí souřadnic. V případě neizotropního dielektrika bude mít vztah mezi vektory D a E tvar
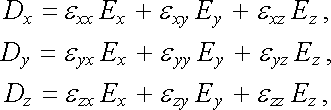 |
(1.261) |
kde veličiny eij (i, j = x, y, z) představují složky tenzoru permitivity. Vlastnosti složek tohoto tenzoru těsně souvisejí s charakterem symetrie krystalu či jiného anizotropního dielektrika. Tato symetrie vede k tomu, že pouze některé ze složek tenzoru jsou nezávislé. Na základě termodynamických úvah (viz např. [7]) lze ukázat, že tenzor (1.261) je obecně symetrický.
Zabývejme se nyní otázkou energie elektrostatického pole v dielektriku, která je analogická problematice energie soustavy nábojů rozložených ve vakuu (viz článek 1.2.8), respektive soustavy nabitých vodičů (viz článek 1.4.6). Připomeňme, že energii dané soustavy jsme definovali pomocí práce, kterou musely vykonat vnější síly při vytváření konečné konfigurace nábojů. Kromě toho bylo vždy možné vyjádřit tuto energii dvěma způsoby: jednak pomocí konečných hodnot nábojů a potenciálů, jednak ve tvaru integrálu typu (1.90) z veličiny we, kterou jsme interpretovali jako objemovou hustotu energie.
V dalších úvahách budeme opět používat oba způsoby, které jsou fyzikálně zcela ekvivalentní, neboť v elektrostatice má fyzikální význam jen celková energie soustavy. Opakujeme znovu, že v rámci elektrostatiky nelze představu o prostorovém rozložení energie ani dokázat, ani vyvrátit.[10]
Uvažujme dielektrické prostředí v elektrostatickém poli; dielektrikum může přitom zaujímat celý prostor nebo jen jeho část. Elektrostatické pole můžeme vyvolat pouze tak, že budeme přivádět do dielektrika volné náboje nebo nabíjet nějaký vodič. Zvětšíme-li náboj takového vodiče o dQ při potenciálu povrchu vodiče j = konst, vykonáme práci dW = j dQ . Podle (1.252) bude v dielektriku u povrchu vodiče platit D.n = s, kde n je jednotkový vektor normály k povrchu vodiče směřující ven do dielektrika. Potom volný náboj na povrchu vodiče bude
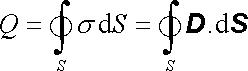 |
(1.262) |
a práci dW můžeme vyjádřit jako
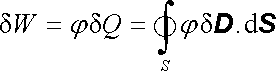 . . |
(1.263) |
Uvažujme nyní konečný objem Vc ohraničený plochou S obklopující daný vodič a obsahující část okolního dielektrika (popř. vakua). V tomto objemu můžeme zavést vektorové pole j dD a aplikovat na něj Gaussovu větu vektorové analýzy. Na povrchu vodiče S je přitom potenciál j konstantní a vektor dD nespojitý. Při aplikaci Gaussovy věty na uzavřený objem musíme proto vyčlenit z objemu Vc objem vodiče, integrovat přes takto vzniklý objem V a uvažovat celkový tok vektoru j dD povrchy S i S:
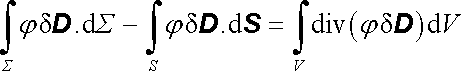 . . |
(1.264) |
Znaménko minus u druhého z integrálů na levé straně souvisí s tím, že normála dS je orientována dovnitř objemu V.
V objemu V neexistují volné náboje a proto zde div (dD) = 0. Můžeme proto upravit integrovanou funkci div (j dD) na
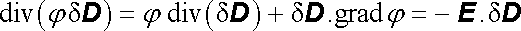 . . |
Budeme-li nyní rozpínat plochu S do nekonečna, zaujme objem V celý prostor (s výjimkou objemu vodiče, kde je ovšem pole dD nulové) a první z integrálů na levé straně (1.264) vymizí z obdobných důvodů, jaké byly uvedeny v článku 1.2.8. Použijeme-li vztah (1.263) , dostaneme pro práci z rov. (1.264)
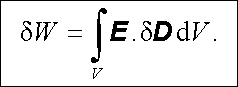 |
(1.265) |
Abychom zjistili celkovou energii nahromaděnou v poli, je třeba integrovat přírůstek dW od počátečního stavu D = 0 do konečné hodnoty D. Pro ideálně měkké, izotropní dielektrikum
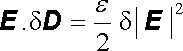 , , |
takže celková energie
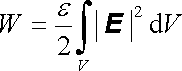 . . |
(1.266) |
Objemovou hustotu energie elektrostatického pole v takovém dielektriku můžeme tedy zapsat ve tvaru
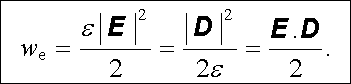 |
(1.267) |
Pro pole ve vakuu se výraz pro hustotu energie redukuje na vztah (1.91) .
Ještě vyšetříme otázku potenciální energie dielektrického tělesa vloženého do vnějšího elektrostatického pole. Tato energie je zřejmě rovna rozdílu energie celé vyšetřované soustavy (s dielektrickým tělesem) a energie této soustavy bez dielektrického tělesa. Označíme-li intenzitu pole bez přítomnosti tělesa symbolem E0, dostaneme podle (1.265) pro přírůstek hledané potenciální energie ve tvaru
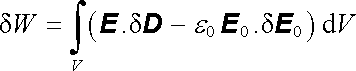 , , |
(1.268) |
přičemž integrujeme opět přes celý objem V, v němž je pole nenulové. Jak je ukázáno například v [6, 7], dá se výraz (1.268) zjednodušit. Provedeme-li totiž formální úpravu integrované funkce
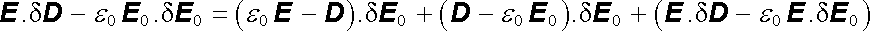 |
a integrujeme přes objem V, zjistíme, že poslední dva členy po integraci vymizí.[11]
Zbude tedy jen integrál členu prvního, který má ovšem nenulový příspěvek jen v objemu dielektrického tělesa Vd. Tedy
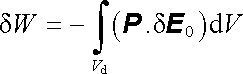 . . |
(1.269) |
Hustota přírůstku potenciální energie pak bude
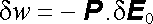 . . |
(1.270) |
Celkovou potenciální energii, respektive její hustotu můžeme spočítat jen v případě, známe-li závislost P na E0 pro dané konkrétní těleso. Situace bude jednoduchá v případě ideálně tvrdého a ideálně měkkého tělesa.
V případě ideálně tvrdého dielektrika vektor polarizace P0 nezávisí na vnějším poli. Pro potenciální energii pak z výrazu (1.269) dostáváme
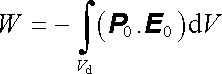 . . |
(1.271) |
Pro ideálně měkké dielektrikum je polarizace úměrná intenzitě pole v dielektriku podle (1.255) . Lze snadno usoudit, že polarizace bude úměrná i vnějšímu poli E0, konstanta úměrnosti k však bude obecně záviset na tvaru tělesa. Před-pokládáme-li tedy P = k E0, můžeme provést integraci
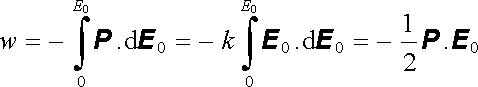 |
(1.272) |
a pro potenciální energii vyjde výsledek
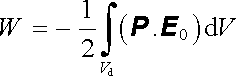 . . |
(1.273) |
V měkkém dielektriku je veličina P.E0 vždy kladná (indukované elektrické dipóly se orientují ve směru vnějšího elektrostatického pole). Ze vztahu (1.273) proto vyplývá, že potenciální energie tělesa z měkkého dielektrika vloženého do vnějšího pole je vždy záporná a klesá s růstem intenzity pole. Takové diele-ktrické těleso bude proto vtahováno do oblasti o větší intenzitě pole. Rozdíl v energii tělesa z ideálně tvrdého a ideálně měkkého dielektrika je zřejmě dán tím, že zatímco v tvrdém dielektriku je polarizace tělesa předem dána a nemění se, v měkkém dielektriku se teprve v poli utváří.
Můžeme též řešit úlohu o chování dielektrického tělesa charakterizovaného permitivitou e1 v jiném dielektrickém prostředí, například kapalném, o per-mitivitě e2. Energie takového tělesa bude pak záviset na vzájemné relaci e1 a e2; bude záporná pro e1 > e2. Naopak tato energie bude kladná při e1 < e2, a v takovém případě bude těleso z pole vypuzováno.
Uvažujme bodový náboj Q umístěný v nekonečném prostoru vyplněném homogenním izotropním dielektrikem. Průběh jím vytvořeného elektrostatického pole určíme snadno pomocí Gaussova zákona (1.247) . Zvolíme-li jako Gaussovu plochu kulovou plochu o poloměru r se středem v místě bodového náboje, snadno usoudíme, že z důvodu symetrie musí mít vektor elektrické indukce D ve všech bodech této plochy konstantní hodnotu a směr normály. Musí platit 4pr2D = Q, takže
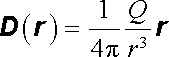 . . |
(1.274) |
Jde-li o ideálně měkké dielektrikum, platí (1.259) a pro intenzitu pole E dostáváme E = (1/4pe)(Q/r3)r. Pro velikost síly F působící mezi dvojicí bo-dových nábojů Q1, Q2 vnořených v ideálně měkkém dielektriku pak zřejmě platí F = (1/4pe)Q1Q2/r2. Intenzita elektrického pole a síla působící mezi bodovými náboji se tedy v takovém dielektriku zeslabí er-krát.
Uvažujme nyní elektrostatické pole soustavy N vodičů nesoucích náboje Q1, Q2,...,QN. Bude nás zajímat, jak se změní toto pole, vyplníme-li prostor obklopující tyto vodiče homogenním, izotropním, měkkým dielektrikem o permitivitě e . Pro povrch každého vodiče platí ve vakuu
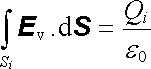 |
(1.275) |
a v dielektriku
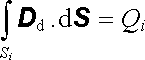 , , |
(1.276) |
kde Ev a Dd jsou odpovídající vektory intenzity pole a elektrické indukce a Si plocha těsně přimykající k povrchu vodiče. Vektory Dv = e0Ev a Dd mají tedy stejné okrajové podmínky na povrchu vodičů. Podle věty o jednoznačnosti řešení základní úlohy elektrostatiky musí tedy platit v každém bodě Dd = e0Ev. Při vyplnění celého prostoru dielektrikem zůstane tedy vektor elektrické indukce nezměněn. Protože však Dd = e Ed, zmenší se intenzita pole e/e0 = er-krát: Ed = (l/er) Ev a stejně tak elektrostatické potenciály v prostoru a na povrchu vodičů.
Nechť plocha S tvoří rozhraní dvou homogenních izotropních dielektrik o permitivitách e1 a e2 (viz obr. 1.63). Vyšetříme průběh elektrostatického pole při přechodu tímto rozhraním. Podle obecného zákona (1.82) budou na ploše S spojité tečné složky intenzity pole. Dále, jelikož na této ploše nejsou volné náboje, budou zde podle (1.254) spojité i normálové složky vektoru elektrické indukce. Vektory E1 a D1 = e1E1 mají týž směr a jejich odklon od směru normály můžeme označit jako úhel q1; podobná úvaha platí pro vektory E2, D2 a úhel q2.

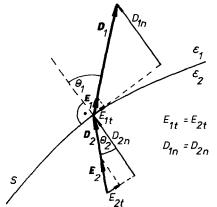
Máme tedy
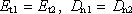 neboli
neboli
 . . |
(1.277) |
Pro vztah mezi úhlem "dopadu a lomu" siločáry elektrostatického pole pak platí
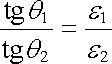 . . |
(1.278) |
Porovnejte tento výraz se Snellovým zákonem pro úhel dopadu a lomu světla (elektromagnetického vlnění).
Mějme nekonečně rozlehlé homogenní dielektrikum o permitivitě e1, v němž působí homogenní elektrické pole E. Do tohoto dielektrika vložíme kouli poloměru R z dielektrika o permitivitě e2. Určeme průběh intenzity výsledného pole uvnitř i vně dielektrické koule. Počátek sférické soustavy souřadnic umístíme do středu koule, osu z namíříme ve směru pole E a úhel q budeme odečítat od tohoto směru.
Můžeme očekávat, že dielektrická koule se ve vnějším homogenním elektrickém poli zpolarizuje s konstantním vektorem polarizace P. Na základě řešení úlohy 1.3.5d bude pole uvnitř koule homogenní a úměrné vnějšímu poli E, pole vně koule bude superpozicí homogenního pole E a pole dipólu p = VP (V je objem koule) sídlícího ve středu koule. Pro pole uvnitř a vně koule máme tedy
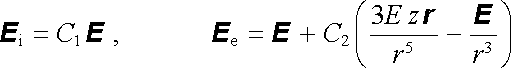 , , |
(1.279) |
kde C1 a C2 jsou konstanty, které máme určit z hraničních podmínek Et1 = Et2, Dn1 = Dn2 na povrchu koule. Z tohoto získáme vztahy
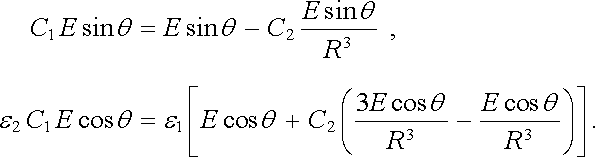 |
Z první podmínky dostaneme vztah mezi konstantami C1 a C2: C1 = 1 - C2/R3 a z druhé podmínky po úpravě C2 = (e2 - e1)R3/(e2 + 2e1). Intenzita pole uvnitř dielektrické koule bude tedy
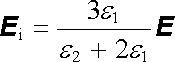 . . |
(1.280) |
Vložíme-li kouli z měkkého dielektrika o relativní permitivitě er do vnějšího elektrického pole E ve vakuu, stačí dosadit do (1.280) e1 = e0, e2 = er e0, pak pro pole uvnitř koule najdeme
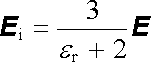 . . |
(1.281) |
K témuž výsledku dospějeme, budeme-li pole uvnitř koule považovat za superpozici původního pole E a pole polarizované koule (1.184) . Potom máme
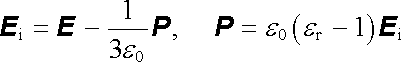 , , |
(1.282) |
odkud vyplývá
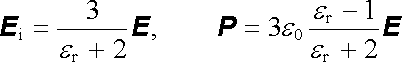 . . |
(1.283) |
Celkový indukovaný dipólový moment koule z měkkého dielektrika je tedy
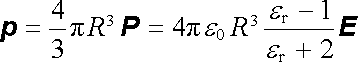 |
a v limitě er (R) yen dává indukovaný moment vodivé koule (1.232) .
Pole uvnitř dielektrické koule zůstává homogenní, ale je oslabeno ve srovnání s původním polem (viz obr. 1.64a). Je to obecná vlastnost dielektrických těles tvaru elipsoidu, včetně degenerovaných případů, k nimž patří například rovinná vrstva nebo válec (podrobněji viz [6], [7] ). Obecně můžeme intenzitu pole v těchto tělesech vyjádřit jako
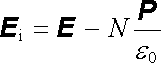 , , |
(1.284) |
kde N označujeme jako depolarizační faktor. Potom
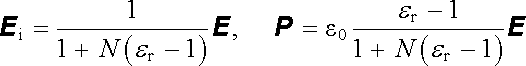 . . |
(1.285) |
V případě rovinné vrstvy kolmé k vnějšímu poli N = 1, pro válec v poli kolmém k jeho ose N = 1/2, pro kouli N = 1/3, pro válec s osou rovnoběžnou s polem N = 0. Je-li tedy těleso velmi protáhlé ve směru pole, jeho depolarizační faktor klesá a pole se neliší od pole bez dielektrika. Naopak v plochém tělese orientovaném kolmo k poli je depolarizační faktor blízký k jedné a pole je rovno E/er.


Chceme určit intenzitu elektrického pole v dutině, která se vytvořila v homo-genním dielektriku o relativní permitivitě er, v němž působí elektrické pole E (obr. 1.64b). Pro kulovou dutinu v měkkém dielektriku můžeme ve vztahu (1.280) položit e1 = e0er, e2 = e0 a obdržíme
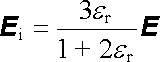 . . |
(1.286) |
Pole v dutině se tedy zesílí, neboť na povrchu dutiny se vytvoří plošný vázaný náboj s = s0 cos q opačného znamení než v případě dielektrické koule. Proto
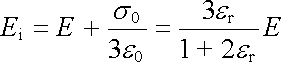 , , |
odkud
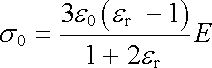 . . |
Opět můžeme ukázat, že bude-li mít dutina tvar protáhlý ve směru pole, bude intenzita pole v dutině přibližně rovna poli v dielektriku E. V ploché dutině kolmé k vnějšímu poli bude pole přibližně rovno er E.
V některých případech je třeba uvažovat myšlený kulový objem vyříznutý v homogenním zpolarizovaném dielektriku tak, že po odstranění dielektrika z tohoto objemu se směr siločar a polarizace vnějšího pole nenaruší. V tom případě zůstane na povrchu dutiny plošný vázaný náboj s = s0 cosq, kde s0 = e0 (er - 1) E a pole v myšlené dutině ve tvaru
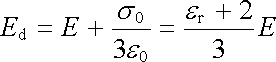 . . |
(1.287) |
Porovnejte tento výraz se vztahem (1.286) .
ÚLOHY KE KAPITOLE 1
Ú 1.1: Určete, jakou silou se přitahují dva nesouhlasné náboje o velikosti e ve vzdálenosti l m. Totéž proveďte pro dva náboje o velikosti l C.
Ú 1.2: Kolikrát je elektrostatická odpudivá síla mezi dvěma elektrony větší než přitažlivá síla gravitační?
Ú 1.3: Dvě kuličky nesoucí náboj q1 a q2 se ve vzdálenosti r přitahují silou o velikosti F1. Po doteku se v téže vzdálenosti odpuzují silou o velikosti F2. Určete náboje q1, q2 (pro určitost uvažujte q1 > 0).
Ú1.4: Na dvou stejných vodních kapkách je po jednom přebytečném elektronu. Přitom síla elektrického odpuzování je stejně velká jako síla gravitačního přitahování. Určete poloměr kapek.
Ú 1.5: Tři stejné náboje q jsou rozmístěny symetricky po obvodu kružnice. Jaký náboj musíme umístit do středu kružnice, aby soustava byla v rovnováze? Bude tato rovnováha stabilní?
Ú 1.6: Tři náboje -e, e, -e jsou umístěny na přímce v uvedeném pořadí ve stejné vzdálenosti a = 10-10 m mezi sousedními náboji. Určete a) sílu působící na každý náboj, b) elektrostatickou potenciální energii soustavy.
Ú 1.7 Najděte takové geometrické uspořádání jednoho protonu a dvou elektronů na přímce, aby potenciální energie soustavy byla nulová.
Ú 1.8 Nechť jsou bodové náboje o velikosti elementárního náboje e, střídavě kladné a záporné, rozloženy podél přímky v rozestupech a = 10-10 m (tzv. lineární krystal). Jaká elektrostatická energie připadá na jeden náboj?
Ú 1.9: Atomové jádro těžkých prvků můžeme z hlediska elektrických vlastností považovat za objemově nabitou kouli s nábojovou hustotou r = 1,3. 1025 C. m-3. Jak se změní elektrostatická energie při symetrickém rozštěpení jádra uranu na dvě stejná jádra atomů palladia?
Ú 1.10: Tenká tyč je umístěna na ose z mezi body z = - a, z = a. Tyč nese náboj o lineární hustotě t. Určete elektrostatický potenciál pro všechny body na ose x pro x > 0.
Ú 1.11: Určete elektrostatické pole a potenciál nekonečně tenkého kruhového kotouče o poloměru R a plošné hustotě s na ose kotouče ve výšce h.
Ú 1.12: Určete elektrostatický potenciál ve středu nekonečně tenké nabité desky čtvercového tvaru o straně a s plošnou hustotou.s. Srovnejte jej s hodnotou potenciálu ve středu kruhového kotouče. (Návod: při integrování rozdělte desku pomocí úhlopříček na čtyři rovnoramenné pravoúhlé trojúhelníky).
Ú 1.13: Z vodivé mýdlové bubliny poloměru 2 cm a nabité na potenciál 104 V vznikne po prasknutí kapka vody o poloměru 0,05 cm. Jak velký bude potenciál kapky?
Ú 1.14: Uvažujte vodivou kouli velikosti Země a vypočítejte její náboj a potenciál, je-li intenzita elektrického pole u jejího povrchu 100 V.m-1, směřuje-li vektor intenzity k povrchu.
Ú 1.15: Jaký maximální náboj se udrží na kovové kouli o poloměru 10 cm, je-li dielektrická pevnost suchého vzduchu 30 kV.cm-1?
Ú1.16: Bodové náboje jsou uspořádány takto: a) ve vrcholech rovnostranného trojúhelníka o straně a v pořadí q, q, -2q; b) ve vrcholech čtverce o straně a v pořadí -q, q, q,-q; c) ve vrcholech čtverce o straně a v pořadí -q, q, -q, q; d) ve vrcholech čtverce o straně a v pořadí -q, 2q, q, -2q. Určete velikost a směr elektrického dipólového momentu těchto soustav.
Ú 1.17: Určete velikost elektrického dipólového momentu lineárního náboje (tenké tyče) délky a, jehož lineární hustota roste lineárně od -t na jednom konci k +t > 0 na druhém konci.
Ú 1.18: Elektrický náboj je rozložen na povrchu koule o poloměru R tak, že na jedné polokouli je kladný náboj konstantní plošné hustoty s, na druhé konstatní záporný náboj hustoty -s. Určete dipólový moment koule.
Ú 1.19: Elektrický dipól p1 je umístěn v počátku souřadnic a je orientován směrem osy z. Dipól p2 leží ve vzdálenosti r na ose x a svírá s ní úhel p/4. Určete velikost a směr síly působící na dipól p2 a potenciální energii této soustavy.
Ú 1.20: Elektrický dipól o momentu p = (0, p, 0) leží v bodě (a, 0, 0) v elektrickém poli bodového náboje q umístěného v počátku. Určete sílu a moment silové dvojice, které budou na dipól působit.
Ú 1.21: Elektrický dipól p v počátku soustavy souřadnic je orientován pod úhlem p/4 k ose x. V bodě A na ose x ve vzdálenosti a umístíme dipól p1, který se může volně otáčet. Jaký úhel s osou x bude svírat v poli dipólu p?
Ú 1.22: Mračno malých rozměrů nesoucí náboj 20 C je ve výšce l km nad povrchem Země. Určete intenzitu elektrostatického pole vzbuzeného tímto nábojem u povrchu Země ve vzdálenosti 3 km od místa, nad nímž se nachází mrak.
Ú 1.23: Kovová koule poloměru R je uzemněna. Ve vzdálenosti 2R od středu koule je umístěn bodový náboj q. Určete náboj q', který bude indukován na kouli.
Ú 1.24: Malá kulička nesoucí náboj 1,67 .10-8 C je ve vzdálenosti 3 cm od rovinné kovové stěny, která je uzemněna. Jakou silou bude kulička ke stěně přitahována? Jakou práci vykonáme, vzdálíme-li tuto kuličku od stěny do nekonečna?
Ú 1.25: Čemu je rovna kapacita Země?
Ú 1.26: Kolik elektronů nese olejová kapička o hmotnosti 10-11g, jestliže je udržována v rovnováze v rovinném kondenzátoru, jehož desky jsou ve vzdálenosti 5 mm od sebe a jsou nabity na potenciální rozdíl 76,5 V (Millikanův pokus)?
Ú l.27: Kolik elektronů se shromáždí na povrchu elektrody kondenzátoru o kapacitě l mF nabitého na napětí l 000 V? Srovnejte řád této veličiny s celkovým počtem volných elektronů v l cm3 mědi.
Ú 1.28: Deskový kondenzátor má kapacitu 600 pF. Jak se tato kapacita změní, vložíme-li mezi desky kondenzátoru rovnoběžně s nimi měděný plech o tloušťce rovné čtvrtině mezery? Má poloha plechu vliv na výsledek?
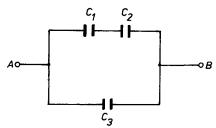
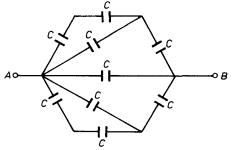
Ú 1.29: Kondenzátory jsou zapojeny podle obr. 1.65. Platí C1 = C2 = 2 mF, C3 = l mF. Určete: a) výslednou kapacitu mezi body A a B, b) maximální dovolené napětí mezi body A a B, je-li kondenzátor C3 dimenzován na l 000 V a C1 , C2 každý na 450 V.
Ú 1.30: Kondenzátory o téže kapacitě C jsou zapojeny podle obr. 1.66. Určete výslednou kapacitu mezi body A a B.

Ú 1.31: Mějme válcový kondenzátor o poloměrech elektrod R1 = 3 cm, R2 = 10 cm nabitý na 450 V. Určete: a) náboj připadající na délkovou jednotku kondenzátoru, b) plošnou hustotu náboje na každém z válců, c) intenzitu elektrostatického pole ve středu vzdálenosti mezi válci.
Ú 1.32 Válcový kondenzátor (Geigerův-Müllerův počítač) je tvořen drátkem poloměru r1 = 0,05 mm v ose válce poloměru r2 = 5 mm. Jaká bude maximální intenzita elektrického pole v trubici, přiložíme-li ke kondenzátoru napětí U = 1000 V?
Ú 1.33: Prostor mezi elektrodami deskového kondenzátoru plochy S je vyplněn dielektrikem, jehož relativní permitivita se mění lineárně od hodnoty e1 u jedné desky k hodnotě e2 < e1 u druhé desky. Vzdálenost desek je d. Určete kapacitu kondenzátoru.

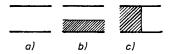
Ú 1.34: Deskový kondenzátor (obr. 1.67a) je zpola zaplněn dielektrikem o permitivitě e dvěma různými způsoby podle obr. 1.67b, c. Určete kapacity v obou případech, je-li kapacita nezaplněného kondenzátoru C0.
Ú 1.35: Indukovaný elektrický dipólový moment kuličky z vosku (er = 3,0) v elektrickém poli je 1,5krát menší než indukovaný moment stejně velké skleněné kuličky. Jaká je relativní permitivita skla?
Ú 1.36: Deskový kondenzátor je zaplněn transformátorovým olejem o rela-tivní permitivitě er = 2,24. Intenzita elektrického pole v kondenzátoru je E = 9,0.106 V.m-1. V oleji vznikne vzduchová bublina. Jaká bude intenzita pole v bublině?
[1] J. C. Zorn a j. Phys. Rev. 129 (1963) , str. 2566, J. G. King, Phys. Rev. Lett. 5 (1960) , str. 562.
[2] Částice a antičástice se liší též znaménkem magnetického momentu a některých dalších tzv. kvantových čísel (leptonový a baryonový náboj, podivnost, půvab aj.), která charakterizují jejich vzájemné interakce. Existuje několik částic, které jsou se svými antičásticemi totožné (například foton) [l].
[3] Poznámka o diferenciálních a integrálních veličinách: Při popisu fyzikálních jevů a formulaci fyzikálních zákonů budeme používat jednak diferenciálního a jednak integrálního tvaru. Diferenciální veličiny jsou přitom definovány jako funkce daného bodu prostoru, zatímco integrální veličiny jsou vázány na předem zadané těleso (plochu, křivku). Náboj Q je tedy veličinou integrální, objemová hustota náboje r veličinou diferenciální.
[4] Uvažujte, jak by se změnilo znázornění elektrostatického pole siločarami v případě, že by v Coulombově zákonu neplatila závislost převrácených čtverců.
[5] Neznamená to samozřejmě, že by se všichni volní nositelé náboje soustředili na povrchu; jakmile je dosaženo nulové intenzity pole v objemu vodiče, uspořádaný pohyb nositelů náboje ustane. Při vzrůstu intenzity vnějšího pole dají se do pohybu další mikroskopičtí nositelé náboje, aby posílili makroskopický povrchový náboj vodiče. Domyšlení této situace vede k hlubšímu pochopení rozdílu mezi makroskopickými a mikroskopickými náboji a poli.
[6] Tato okolnost může vést ke známému "sršení elektřiny z hrotů" nebo naopak slouží jako princip bleskosvodu.
[7] S. J. Plimpton, W. E. Lawton: Phys. Rev. 50 (1936) , 1066.
[8] Podrobněji je o těchto otázkách pojednáno například v knize Scott W. T.: The Physics of Electricity and Magnetism, J. Wiley, New York 1966.
[9] Všimněme si, že zatímco rovnice rot E = 0, resp. Rot E = 0 mají obecnou platnost, nemůžeme udat obecně platné vztahy pro rot D, resp. Rot D.
[10] Vtipnou analogii autorů Masona a Weavera uvádí Stratton v [6]. Kladou otázku, zda je možné tvrdit, že krása obrazu je rozprostřena po celé jeho ploše s danou plošnou hustotou. Odpověď není přitom zdaleka jednoduchá; půjde-li například o holografický záznam obrazu, víme, že každá jeho část obsahuje informaci o celém obrazu.
[11] Při integrování druhého členu vyjádříme dE0 jako gradient potenciálu a integrujeme per partes, takže dostaneme součet plošného a objemového integrálu. Objemový integrál vymizí vzhledem k tomu, že v integrovaném objemu nejsou náboje a divergence D i E0 jsou tam nulové, plošný integrál se počítá jednak po nekonečně vzdálené ploše, jednak po povrchu vodičů vytvářejících pole E0 , kde jsou konstantní potenciály. V obou případech dá výsledek integrování nulu. Podobně se lze vyrovnat i s integrálem třetího členu.