Elektrickým dipólem se obyčejně rozumí soustava dvou bodových nábojů Q- < 0, Q+ > 0 stejné velikosti Q, ale opačného znamení, umístěných v bodech r-, r+ ve vzájemné vzdálenosti l. Pokud chceme vyšetřit elektrické pole dipólu, označíme k tomu účelu vektor l = r+ - r- a zavedeme elektrický dipólový moment vztahem
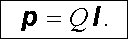 |
(1.121) |
Dipól umístíme v počátku soustavy souřadnic tak, že vektor l, který míří od záporného náboje ke kladnému, bude orientován v kladném směru osy z a počátek bude půlit délku l.
Osa z je osou symetrie dipólu. Jeho elektrostatické pole bude tedy také osově symetrické se stejnou osou symetrie. Stačí tedy vyšetřit potenciál j(r) v libo-volném bodě A roviny x z (viz obr. 1.27). Podle vztahu (1.48) , položíme-li C = 0, platí
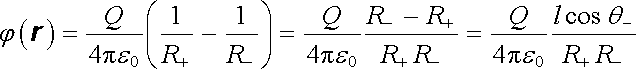 , , |
(1.122) |
kde q-, q a q+ jsou úhly mezi osou z a vektory R-, r a R+.
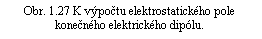
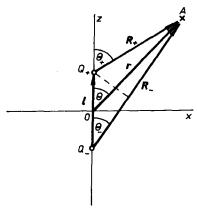
Předpokládejme nyní, že vzdálenost bodu A od dipólu je mnohem větší než jeho rozměr, tj. r >> l. Potom zřejmě platí přibližné vztahy
 , , |
(1.123) |
a tedy
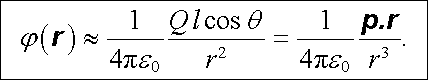 |
(1.124) |
Přitom poslední tvar platí obecně pro dipól v počátku soustavy souřadnic, nezávisle na orientaci p vůči osám.
V limitě, kdy l (R) 0 a p zůstává konečný, vznikne bodový útvar, jehož elektrostatické pole je přesně dáno vztahem (1.124) . Nazýváme jej bodovým elektrickým dipólem. Vedle bodového náboje představuje tento dipól další velmi důležitý bodový, ovšem v prostoru orientovaný, útvar používaný k chara-kteristice reálných soustav nábojů. Dipólový moment měříme v jednotkách coulomb metr [C.m]. Zatímco potenciál bodového náboje klesá s první mocninou vzdálenosti, potenciál bodového dipólu klesá podle (1.124) s její druhou mocninou.
Intenzitu pole bodového dipólu určíme ze vztahu (1.124) podle rov. (1.50) . Použijeme-li výraz (D 1.55) pro gradient skalárního součinu, dostaneme přímým výpočtem
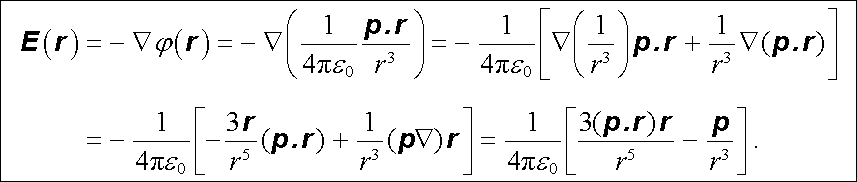 |
(1.125)
V konfiguraci podle obr. 1.27 platí pro bodový dipól p = (0, 0, p), r = (x, 0, z), cos q = z/r, sin q = x/r a složky intenzity v rovině x y můžeme explicitně vyjádřit ve tvaru
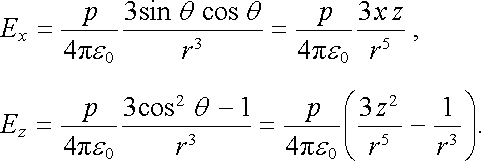 |
(1.126) |
Siločáry tohoto pole jsou znázorněny na obr. 1.28. Snadno ověříme, že pro body na ose z (q = 0) platí
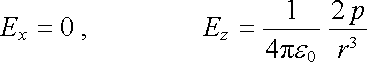 |
(1.127a) |
a pro body na ose x (q = p/2)
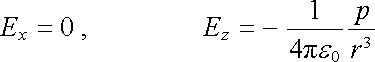 . . |
(1.127b) |

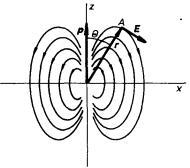
Nyní vyšetříme síly působící v elektrostatickém poli na elektrický dipól. Díky tomu, že vzdálenost l je neměnná, můžeme na dipól pohlížet jako na tuhou soustavu. V již zavedeném označení (viz obr. 1.29) můžeme vyjádřit síly působící na jednotlivé náboje ve tvaru F+ = Q E(r+), F- = -Q E(r). Podle pravidel známých z mechaniky tuhého tělesa můžeme obě tyto síly přenést do jednoho bodu, vektorově je složit a jejich výslednici doplnit dvojicí sil vhodného momentu.
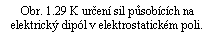

Přeneseme-li sílu F+ do bodu r-, dostaneme pro výslednici
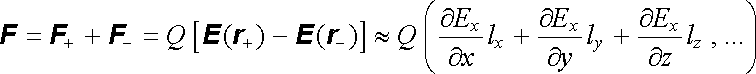 |
neboli (viz (D 1.54))
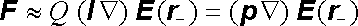 . . |
(1.128) |
Dynamický účinek výslednice F je podle zmíněných pravidel mechaniky třeba doplnit silovou dvojicí momentu
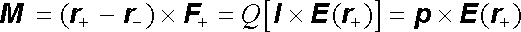 . . |
(1.129) |
Podobně můžeme určit i potenciální energii elektrického dipólu ve vnějším elektrostatickém poli. Potenciální energii obou bodových nábojů Q+, Q- ve vnějším poli můžeme podle (1.56) zapsat jako
 . . |
(1.130) |
Potenciální energie dipólu pak bude
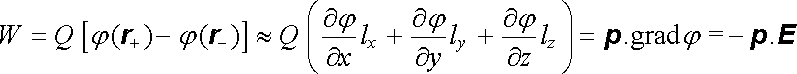 . . |
(1.131)
Přitom jsme neuvažovali vzájemnou interakční energii obou nábojů tvořících dipól, neboť jej bereme jako tuhý celek, bez možnosti deformace.
Pro bodový elektrický dipól popsaný pouze vektorem p zůstávají všechny tři vztahy (1.128) , (1.129) , (1.131) samozřejmě v platnosti, a to přesně:
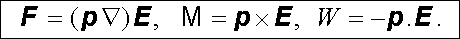 |
(1.132) |
Potenciální energie mechanické soustavy je dána její geometrickou konfigurací, kterou můžeme popsat geometrickými parametry zvanými obecné souřadnice. Speciálně, nachází-li se bodový elektrický dipól ve vnějším elektrostatickém poli, bude jeho poloha popsána například polohovým vektorem r (tj. třemi kartézskými souřadnicemi x, y, z) a úhlem q, který svírá vektor p s vektorem intenzity pole E. (Důsledně vzato, měli bychom udat ještě azimutální úhel j v rovině kolmé k E; vzhledem k osové symetrii potenciální energie dipólu však na tomto úhlu nezávisí.)
Derivací potenciální energie podle obecných souřadnic qi dostáváme tak zvané obecné síly
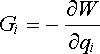 . . |
(1.133) |
Obecnými silami mohou být například složky obyčejných sil, složky momentu síly apod. Tak pro bodový náboj Q máme
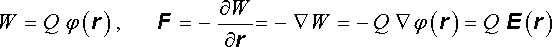 . . |
(1.134) |
Pro bodový dipól pak užitím potenciální energie W = -p.E dostaneme pomocí vztahu (D 1.55)
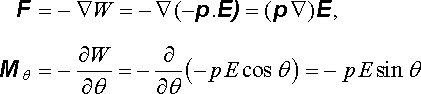 |
(1.135) |
v souladu s prvními výrazy (1.132) . Záporné znaménko silového momentu vyjadřuje fakt, že tento moment působí ve směru klesajícího úhlu .

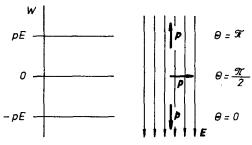
Výrazy pro sílu a moment síly působící na dipól ve vnějším elektrostatickém poli ukazují, že v homogenním poli, kdy E = konst, je síla působící na dipól nulová a uplatní se pouze moment síly. Tento moment se snaží zmenšit úhel q mezi směrem dipólu a směrem siločar pole. Potenciální energie dipólu je v tomto případě čistě orientační. Nechť úhlu q = p/2 odpovídá například nulová potenciální energie. Budeme-li natáčet dipól vzhledem k siločarám, budeme konat práci
(eq0174); (1.136)
tato práce (kladná či záporná) se bude měnit v potenciální energii dipólu. Tak úhlu q = p bude odpovídat maximální potenciální energie W = pE , úhlu q = 0 minimální potenciální energie W = -pE (viz obr. 1.30), a tedy stav stabilní rovnováhy.

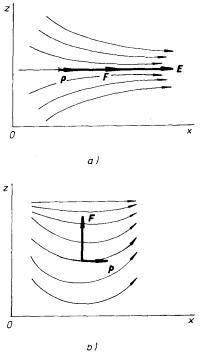
V nehomogenním elektrostatickém poli působí na elektrický dipól nenulová síla. Pro ilustraci charakteru této síly uvažme zvláštní případ nehomogenního pole, jehož siločáry původně rovnoběžné s osou x se v tomtéž směru sbíhají a zhušťují kolem osové siločáry (viz obr. 1.31a). Vektor gradientu pole míří tedy rovněž ve směru osy x. Umístíme-li na osové siločáře elektrický dipól orientovaný ve směru siločar, bude na něj působit síla
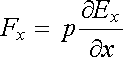 |
(1.137) |
v kladném směru osy x. Bude-li mít dipól opačnou orientaci, změní se i směr síly na opačný. Jiný případ nehomogenního pole je znázorněn na obr. 1.31b. Směr pole a jeho gradient jsou v tomto případě vzájemně kolmé. Na dipól orientovaný ve směru siločar bude tentokrát působit síla
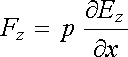 |
(1.138) |
v kladném směru osy z, při změně orientace dipólu se změní i směr síly.
Souhrnně je tedy možné říci, že elektrický dipól orientovaný souhlasně se směrem intenzity elektrostatického pole je vtahován do oblasti o větší intenzitě pole, dipól orientovaný nesouhlasně je z této oblasti vytlačován. Volný obecně orientovaný dipól se působením silového momentu nejprve natočí do směru pole a pak bude vtahován do oblasti o větší intenzitě.
 Vraťme
se nyní k úloze zkoumané v článku 1.2.4, tj. určit elektrostatické pole
a potenciál libovolně rozložených nábojů. Na obrázku 1.32 je znázorněn
objem V, v němž je rozložen elektrický náboj s objemovou hustotou r(rc).
Máme určit například potenciál vytvářený objemem V v bodě A,
který pro zjednodušení postupu umístíme na ose z ve vzdálenosti r
od počátku. Víme již, že k určení potenciálu jA = j(r)
musíme integrovat přes objem V podle výrazu
(1.70a)
. Body o polohovém
vektoru rc přitom probíhají objem V;
rozdíl vektorů r - rc označíme
jako R, úhel mezi vektorem rc a vektorem r
(osou z) jako q. Pro velikost R
podle kosinové věty platí
Vraťme
se nyní k úloze zkoumané v článku 1.2.4, tj. určit elektrostatické pole
a potenciál libovolně rozložených nábojů. Na obrázku 1.32 je znázorněn
objem V, v němž je rozložen elektrický náboj s objemovou hustotou r(rc).
Máme určit například potenciál vytvářený objemem V v bodě A,
který pro zjednodušení postupu umístíme na ose z ve vzdálenosti r
od počátku. Víme již, že k určení potenciálu jA = j(r)
musíme integrovat přes objem V podle výrazu
(1.70a)
. Body o polohovém
vektoru rc přitom probíhají objem V;
rozdíl vektorů r - rc označíme
jako R, úhel mezi vektorem rc a vektorem r
(osou z) jako q. Pro velikost R
podle kosinové věty platí
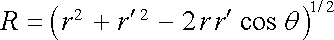 , , |
(1.139) |
a tedy
 , , |
(1.140) |
kde
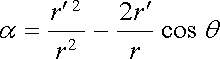 . . |
(1.141) |
V případě obecně, tj. nepravidelně, rozloženého náboje může integrování výrazu pro potenciál činit potíže. Někdy navíc ani neznáme přesné rozložení náboje v prostoru r(rc). Naproti tomu se často můžeme spokojit s nalezením potenciálu a intenzity pole ve vzdálenostech, které značně převyšují rozměry objemu V, tedy pro něž platí rc/r << l, a << 1. Takový případ nastává například, zkoumáme-li elektrostatické pole molekul, atomů, atomových jader.
Výraz 1/R, který vystupuje v integrálu (1.70a) , můžeme pak rozvinout podle binomické věty do řady s členy o postupně klesající velikosti
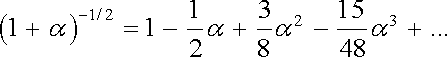 |
(1.142) |
Vyjádříme-li explicitně členy této řady a zachováme-li pouze veličiny do druhého řádu vzhledem k podílu rc/r, dostaneme
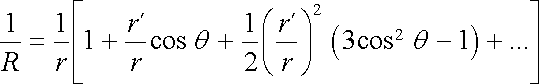 . . |
(1.143) |
Potenciál jA můžeme také napsat ve tvaru nekonečné řady
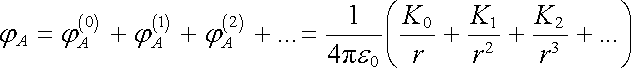 . . |
(1.144) |
Veličiny Ki jsou dány odpovídajícími integrály přes objem V a závisí pouze na způsobu rozložení náboje v tomto objemu. Nazývají se elektrickými multipólovými momenty a řada (1.144) představuje multipólový rozvoj elektrostatického pole. Multipólové momenty jsou konečné a jejich příspěvek k potenciálu jA klesá s odpovídající mocninou vzdálenosti r. Lze dokázat, že uvedený rozvoj potenciálu konverguje a že elektrostatické pole libovolné ohraničené soustavy nábojů ve velkých vzdálenostech lze vždy jednoznačně rozložit na příspěvky jednotlivých multipólových momentů. Tyto momenty představují elektrické charakteristiky daného nabitého objemu (molekuly, atomu, atomového jádra apod.) a je možné je určovat též experimentálně. Tím je dána možnost porovnávat vypočtené hodnoty těchto charakteristik se změřenými.
Uvedeme explicitně první tři multipólové momenty a ukážeme jejich fyzikální význam:
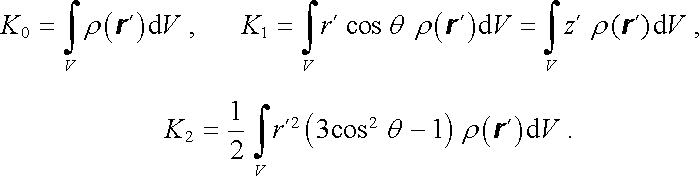 |
(1.145) |
Integrál K0 představuje zřejmě celkový elektrický náboj soustavy Q; tento náboj můžeme tedy považovat za elektrický "monopól". Je-li tento integrál, a tedy celkový náboj, nenulový, bude pole ve velkých vzdálenostech od nabitého objemu v prvním přiblížení totožné s polem bodového náboje Q. Tento triviální závěr vyjadřuje vlastně definici pojmu bodového náboje.
Integrál K1 můžeme považovat za složku pz vektorové veličiny p, kterou nazveme elektrický dipólový moment. Definujeme jej podle toho, zda jsou náboje rozloženy spojitě či nespojitě jako
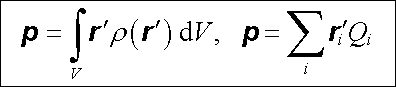 |
(1.146) |
(
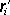 jsou polohové vektory bodových nábojů Qi;
srov. vztah
(1.121)
).
jsou polohové vektory bodových nábojů Qi;
srov. vztah
(1.121)
).

Vzniká otázka, zda
takto definovaná veličina bude invariantní vůči změně počátku souřadnic či
nikoli. Změníme-li počátek souřadnic z O na Oc tak,
že polohové vektory
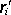 budou nahrazeny polohovými vektory
budou nahrazeny polohovými vektory
 ,
,
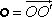 (viz obr. 1.33), dostaneme
(viz obr. 1.33), dostaneme
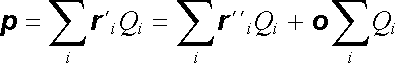 . . |
(1.147) |
Vidíme tedy, že elektrický dipólový moment soustavy bude invariantní veličinou pouze v tom případě, bude-li celkový náboj soustavy roven nule, tj. bude-li soustava jako celek elektricky neutrální. V takovém případě bude potenciál ve velkých vzdálenostech v prvním přiblížení roven
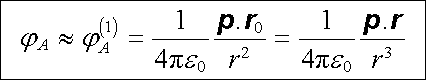 |
(1.148) |
(r0 = r/r je jednotkový vektor ve směru r), což je výsledek totožný se vztahem (1.124) .
Může se stát, že jak celkový náboj soustavy, tak i její elektrický dipólový moment budou nulové. V tom případě bude pole v prvním přiblížení určeno dalším členem multipólového rozvoje, tj. členem K2, viz vztahy (1.145) . Veličinu 2K2 můžeme považovat za komponentu nějaké tenzorové veličiny, kterou nazýváme elektrický kvadrupólový moment soustavy. Můžeme ji vyjádřit symetrickou maticí
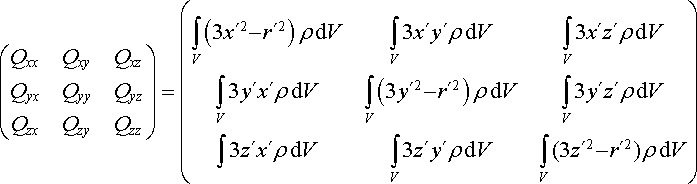 . . |
(1.149) |
Potom zřejmě
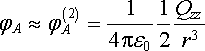 . . |
(1.150) |
Také pro elektrický kvadrupólový moment lze dokázat, že je invariantní vůči změně počátku soustavy souřadnic, pokud Q = 0 a p = 0.
Označíme-li xc = x1, yc = x2, zc = x3 a použijeme-li tzv. Kroneckerův symbol dij, kde
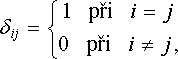 |
(1.151) |
můžeme složky kvadrupólového momentu pro spojité rozložení nábojů s hustotou r a nespojité rozložení N nábojů Qa vyjádřit jako
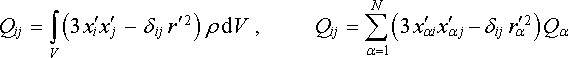 . . |
(1.152) |
Ze vztahů (1.152) snadno zjistíme, že součet diagonálních složek Qij (tzv. stopa tenzoru) je roven nule. Zvolíme-li kromě toho osy soustavy souřadnic tak, aby všechny nediagonální složky Qij byly rovny nule (tzv. hlavní osy), a je-li například osa z osou rotační symetrie daného rozložení nábojů, dostaneme
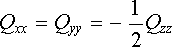 |
(1.153) |
a jediná složka Qzz pak plně charakterizuje kvadrupólový moment soustavy.
Jsou-li všechny tři první integrály K0, K1, a K2, tedy celkový náboj, dipólový i kvadrupólový moment, nulové, musíme přejít k dalším multipólovým momentům - oktupólovému, popř. vyšším. Tato pole vyšších multipólů se však uplatní jen ve speciálních případech a kromě toho velmi rychle ubývají se vzdáleností.
Rozklad pole na příspěvky jednotlivých multipólů má úzký vztah k symetrii rozložení náboje. Při přechodu k vyšší symetrii mizí postupně stále větší počet nižších multipólových momentů. Nejvyšší symetrii vykazuje koule poloměru R rovnoměrně nabitá celkovým nábojem Q. Z důvodů této symetrie jsou její dipólový a všechny ostatní multipólové momenty nulové a její pole v libovolné vzdálenosti r > R je přesně totožné s polem bodového náboje Q umístěného ve středu koule. Tento výsledek jsme již zjistili v příkladu 1.2.9f.
Podobně jako jsme zaváděli plošnou a objemovou hustotu elektrického náboje, můžeme uvažovat i bodové elektrické dipóly spojitě rozložené na dané ploše S či v objemu V. Plošné rozložení elektrických dipólů nazýváme elektrickou dvojvrstvou. Jednotce takové plochy pak můžeme přisoudit určitý elektrický dipólový moment a zavést tak plošnou hustotu dipólového momentu pS(r). Je-li tato plošná hustota co do velikosti konstantní a má všude směr normály k ploše S, nazýváme takovou elektrickou dvojvrstvu homogenní.
K pojmu homogenní elektrické dvojvrstvy můžeme opět dospět limitním přechodem podobně, jako jsme dospěli k pojmu bodového elektrického dipólu. Uvažujme velmi tenkou desku konstantní tloušťky Dl vymezenou dvojicí ploch S1 , S2 (viz obr. 1.34). Nechť plocha S1 je nabita kladným nábojem rozloženým s konstantní plošnou hustotou s > 0 a podobně plocha S2 záporným nábojem s plošnou hustotou -s . Nechť dále n je jednotkový vektor normály plochy S2 v daném bodě orientovaný směrem k ploše S1. Potom zřejmě můžeme v každém bodě plochy S2 definovat veličinu
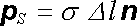 , , |
(1.154) |

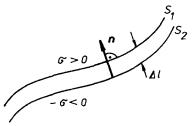
kterou nazveme plošnou hustotou dipólového momentu. Limitním přechodem, při němž Dl (R) 0, obě plochy S1 a S2 splynou v jedinou plochu S a vektor pS si zachová v každém bodě plochy svou původní hodnotu, dospějeme k pojmu homogenní elektrické dvojvrstvy. Tato dvojvrstva představuje tedy elektricky neu-trální plochu, jejíž jedinou charakteristikou je vektor pS.
Elektrostatický potenciál dvojvrstvy v libovolném bodě prostoru neležícím na ploše dvojvrstvy můžeme získat analogickým postupem, jako jsme dospěli k výrazu (1.70b) . Protože potenciál bodového dipólu je dán (přesně) vztahem (1.124) , bude potenciál vyvolaný celou dvojvrstvou v bodě A dán integrálem
(eq0197); (1.155)
vektor R míří z elementu dvojvrstvy dS do bodu A, vektor rc je polohový vektor elementu dS a R = r - rc. V případě homogenní dvojvrstvy máme (platí pS = pS n, dS = n dS)
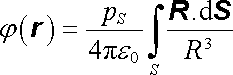 . . |
(1.156) |

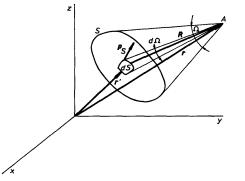
Integrál na pravé straně (1.156) má čistě geometrický význam a vyjadřuje prostorový úhel W, pod nímž je vidět plocha dvojvrstvy z bodu A. Skutečně pro plošku dS a element prostorového úhlu dW platí vztah
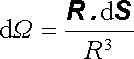 |
(1.157) |
a integrací přes celou plochu S dostaneme
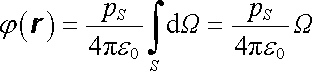 |
(1.158) |
(viz obr. 1.35).
Získaný výsledek vyjadřuje podivuhodnou vlastnost dvojvrstvy: elektrostatické pole jí vytvářené v daném bodě prostoru se nezmění při libovolných deformacích dvojvrstvy, pokud přitom zůstane zachován celkový zorný úhel W. Z výrazu (1.155) plyne, že potenciál dvojvrstvy je spojitý všude s výjimkou plochy S. Při průchodu touto plochou se mění prostorový zorný úhel libovolné její části dS nespojitě o hodnotu 4p. Potenciál má zde tedy nespojitost pS/e0.
Může nastat i
složitější situace, kdy plocha dvojvrstvy je z daného bodu vidět částečně z
jedné a částečně z druhé strany. Plochu S přitom můžeme orientovat tím,
že směr vektoru
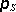 prohlásíme za kladný. Abychom zachovali
vlastnost potenciálu dvojvrstvy vyjádřené vztahem
(1.158)
, musíme potom zornému
úhlu té části plochy, která je vidět z kladné strany, připsat kladné znaménko a
té části, která je vidět ze záporné strany, znaménko záporné. Tvoří-li
elektrická dvojvrst-va uzavřenou plochu, pak pro body vně dvojvrstvy bude
zřejmě W
= 0, pro body uvnitř W = 4p. Potenciál vně uzavřené dvojvrstvy je tedy roven nule,
potenciál uvnitř uzavřené dvojvrstvy je konstantní a roven pS/e0.
prohlásíme za kladný. Abychom zachovali
vlastnost potenciálu dvojvrstvy vyjádřené vztahem
(1.158)
, musíme potom zornému
úhlu té části plochy, která je vidět z kladné strany, připsat kladné znaménko a
té části, která je vidět ze záporné strany, znaménko záporné. Tvoří-li
elektrická dvojvrst-va uzavřenou plochu, pak pro body vně dvojvrstvy bude
zřejmě W
= 0, pro body uvnitř W = 4p. Potenciál vně uzavřené dvojvrstvy je tedy roven nule,
potenciál uvnitř uzavřené dvojvrstvy je konstantní a roven pS/e0.
Intenzitu elektrostatického pole vytvářeného dvojvrstvou můžeme určit buď jako záporně vzatý gradient potenciálu (1.155) , popř. (1.156) , nebo přímo integrací výrazu (1.125) :
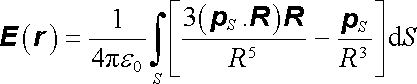 . . |
(1.159) |
I pro intenzitu pole musí platit, že závisí pouze na celkovém zorném úhlu W, pod nímž je vidět plochu dvojvrstvy, a tedy pouze na tvaru hranice této plochy. Podrobnější rozbor, který nebudeme provádět (viz např. [4]), ukazuje, že integrál po ploše dvojvrstvy lze skutečně převést na integrál podél uzavřené hraniční křivky a lze psát
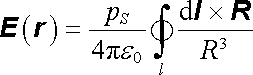 . . |
(1.160) |
Smysl oběhu křivky l při integraci je dán orientací plochy S. Ze vztahu (1.160) plyne, že intenzita je spojitá všude s výjimkou hranice l, tedy i v bodech plochy dvojvrstvy S.
Uvažujme objem V, v němž jsou spojitě rozloženy elektrické dipóly. Opět můžeme zřejmě zavést vektorovou funkci P(r), která bude vyjadřovat objemovou hustotu elektrických dipólů, resp. elektrický dipólový moment jednotky objemu v daném bodě. Této vektorové funkci říkáme vektor polarizace. Podle fyzi-kálního smyslu tohoto vektoru bude elektrický dipólový moment malého objemu DV roven
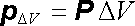 . . |
(1.161) |
Jsou-li v objemu V stejné bodové dipóly p rozloženy s koncentrací N(rc) a všechny orientovány souhlasně, bude platit
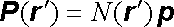 . . |
(1.162) |
Vektor P můžeme ovšem zavést i v případě, když dipólové momenty nebudou souhlasně orientovány. Kdyby byly dipóly rozloženy co do orientace dokonale chaoticky, vzájemně by se kompenzovaly a výsledný vektor polarizace by byl nulový.
Vznik objemového rozložení elektrického dipólového momentu si můžeme představit též tímto způsobem. Nechť jsou v objemu V současně rozloženy kladné náboje s objemovou hustotou r(rc) a záporné náboje s objemovou hustotou -r(rc) o stejné absolutní hodnotě v každém bodě. Posune-li se nyní všechen kladný náboj vůči zápornému o malou vzdálenost Dl, můžeme v každém bodě rc definovat veličinu P(rc) = r(rc)Dl, která má zřejmě význam objemové hustoty elektrického dipólového momentu. Situace zřejmě odpovídá již zmíněnému případu souhlasně orientovaných bodových dipólů, kdy vektor P má v celém objemu týž směr.
Všimněme si ještě zajímavé okolnosti, že polarizace má fyzikální rozměr shodný s rozměrem plošné hustoty elektrického náboje a měří se tedy v jednotkách coulomb na čtverečný metr.
Určíme nyní potenciál j(r) vytvářený polarizovaným objemem V v libovolném bodě r. Potenciál opět vyjádříme integrálem analogickým k výrazu (1.70a) s využitím vztahu (1.124) . Vektor rc bude opět probíhat integrovaným objemem V, a označíme R = r - rc. Dostaneme
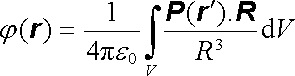 . . |
(1.163) |
Integrovanou funkci můžeme upravit použitím známých vztahů vektorové analýzy. Platí jednak
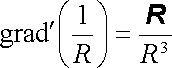 , , |
(1.164) |
jednak vztah pro divergenci součinu skalární a vektorové funkce (D 1.37), s jehož pomocí dostáváme
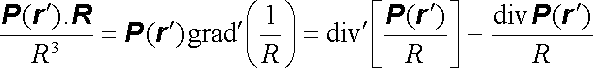 |
(1.165) |
(čárka u symbolů grad a div označuje, že derivování se zde provádí podle souřadnic vektoru rc; vektor r považujeme za konstantní).
Provedený rozklad nám umožní vyjádřit potenciál polarizovaného objemu ve velmi názorné podobě. Máme
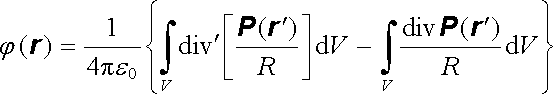 |
(1.166) |
a upravíme-li první integrál podle Gaussovy věty vektorové analýzy (jako S označíme uzavřenou plochu omezující objem V), dostaneme konečný výsledek
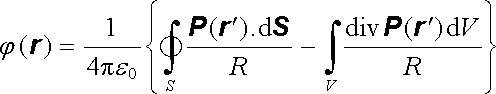 . . |
(1.167) |
Zaveďme plošnou hustotu náboje s(rc) na povrchu objemu V (n budiž jednotkový vektor normály k ploše S orientovaný směrem ven) a objemovou hustotu náboje vztahy
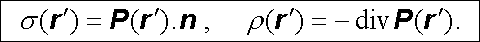 |
(1.168) |
Potom můžeme (1.167) zapsat jako
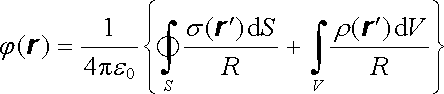 . . |
(1.169) |
Integrály na pravé straně však vyjadřují potenciál vytvářený plošně a objemově rozloženými náboji s hustotami, danými vztahy (1.168) .
Můžeme tedy celkově říci: Elektrostatické pole dipólů objemově rozložených v objemu V s hustotou P(rc) lze formálně popsat jako superpozici elektrostatického pole nábojů objemově rozložených v tomto objemu s hustotou r = -div P a elektrostatického pole nábojů plošně rozložených na povrchu S uvažovaného objemu V s hustotou s = P.n, kde n je jednotkový vektor kladné normály. V článku 1.3.5 uvedeme některé konkrétní příklady demonstrující tuto možnost.
Ve speciálním případě homogenního rozložení, kdy hustota P je v celém objemu V konstantní, je zřejmě div P = 0. Potenciál je pak dán jen plošným integrálem z pravé strany vztahu (1.169) a pole vytvářené polarizovaným objemem je pak ekvivalentní poli uvedeného plošného náboje.
Důležitá je též ta okolnost, že potenciál (1.163) a z něho odvozená intenzita pole jsou definovány nejen ve vnějším prostoru, ale i uvnitř polarizovaného objemu, všude, kde je nulová plošná hustota náboje, viz (1.168) .
Mějme dva elektrické dipóly o momentech p1 a p2 ve vzdálenosti r. Určeme sílu vzájemného působení mezi nimi. Dipól p1 vytváří elektrostatické pole dané výrazem (1.125) . Dipól p2 se nachází v tomto poli a podle vztahů (1.132) naň tedy působí síla
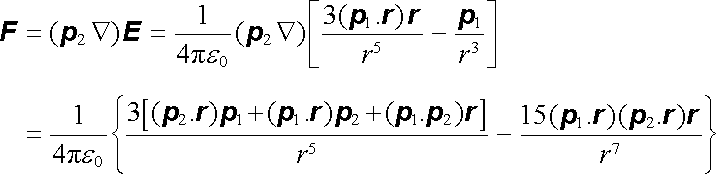 |
(1.170) |
(vektor r míří od p1 k p2).

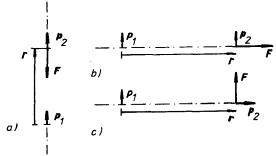
Tento obecný vzorec pro sílu působící ze strany dipólu p1 na dipól p2 není dosti názorný. Všimněme si proto tří speciálních případů, kdy jsou oba dipóly orientovány určitým způsobem vůči sobě navzájem a vůči vektoru r (viz obr. 1.36):
l. Oba dipóly leží v jedné přímce a jsou souhlasně orientovány (obr. 1.36a). Podle výrazu (1.170) bude síla, kterou působí dipól p1 na dipól p2, přitažlivá o velikosti
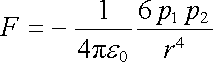 . . |
(1.171) |
(Znaménko minus vyjadřuje přitažlivý charakter síly.)
2. Oba dipóly jsou souhlasně orientovány ve směru kolmém ke spojnici, tj. k vektoru r (obr. 1.36b). V tomto případě bude síla působící na dipól p2 odpudivá a její velikost bude rovna
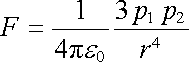 . . |
(1.172) |
3. Dipól p1 je orientován kolmo ke spojnici, vektor p2 rovnoběžně s ní (obr. 1.36c). Síla působící na dipól p2 není v tomto případě centrální, míří kolmo ke spojnici a má velikost
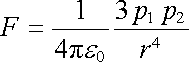 . . |
(1.173) |
Síla mezi bodovými elektrickými dipóly je tedy prvním příkladem necentrálních sil, s nímž jsme se setkali. Tato okolnost má zajímavý důsledek. Budeme-li dipóly p1 , p2 vzájemně orientované jako ve třetím uvažovaném případě přibližovat k sobě z nekonečna, nebudeme přitom konat práci (síla a dráha jsou vzájemně kolmé!). Potenciální energie soustavy dvou dipólů bude pak pouze výsledkem práce konané při vzájemném natáčení dipólů v jejich konečných polohách. Tuto energii můžeme určit podle vztahů (1.132) a (1.125) jako
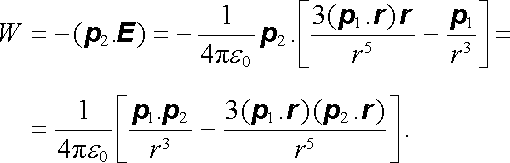 |
(1.174) |
Víme, že elektrický dipólový, kvadrupólový a všechny vyšší multipólové momenty objemově nabité koule s konstantní objemovou hustotou r jsou nulové. Situace se může změnit, dojde-li k deformaci koule, tj. k odchylce od sférické symetrie. Uvažme proto elipsoid, jehož povrch je dán rovnicí
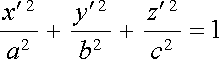 , , |
(1.175) |
nabitý objemově s hustotou náboje r. Osy souřadnic nechť mají počátek ve středu elipsoidu a jsou totožné s jeho hlavními osami. Určeme nejprve elektrický dipólový moment elipsoidu, jehož složky podle (1.146) jsou dány integrály
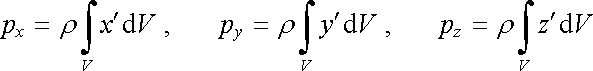 |
(1.176) |
přes objem elipsoidu. Pro usnadnění integrování přejdeme k souřadnicím x = xc/a, y = yc/b, z = zc/c, a tím k integrování přes objem koule o jednotkovém poloměru. Přitom se používá sférických souřadnic r, q, j, které jsou vázány s kartézskými souřadnicemi vztahy x = r sin q cos j, y = r sin q sin j, z = r cos q. Souřadnice q je úhel, který svírá průvodič daného bodu s osou z a j je azimutální úhel průvodiče v rovině x y. Element objemu vyjádřený ve sférických souřadnicích má tvar
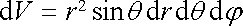 . . |
(1.177) |
Pak dostáváme
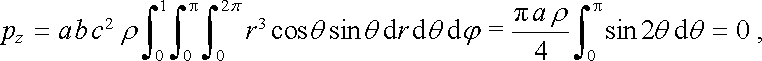 |
(1.178) |
podobné výrazy získáme pro další složky. Zjišťujeme, že elektrický dipólový moment elipsoidu je nulový.
Nenulovými složkami kvadrupólového momentu při zvolených osách mohou být pouze složky diagonální. Tak dostaneme například
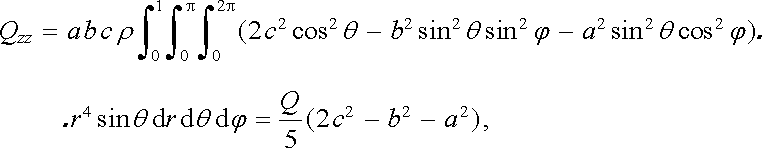 |
(1.179) |
kde Q = (4/3)pabcr je celkový náboj elipsoidu. Cyklickou záměnou a, b, c dostaneme i ostatní nenulové složky Qxx, Qyy.
Jde-li o rotační elipsoid s osou rotační symetrie z, potom a = b a jedinou nezávislou složkou elektrického kvadrupólového momentu je
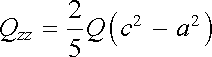 . . |
(1.179a) |
Tato veličina se používá například k vyjádření elektrické nesféričnosti atomových jader. Jinak otázka dipólového, popř. kvadrupólového, momentu elemen-tárních částic a systémů z nich složených je velmi závažná a souvisí s experi-mentálním i teoretickým studiem jejich struktury.
Mějme objem v podobě kolmého válce o obecném tvaru podstavy spojitě zaplněný bodovými elektrickými dipóly tak, že vektor polarizace P je konstantní a rovnoběžný s osou válce. Podle vztahů (1.168) a (1.169) bude elektrostatické pole vytvářené takovým objemem totožné s polem dvou plošných nábojů představovaných horní podstavou válce nabitou nábojem o plošné hustotě s+ = P a dolní podstavou válce nabitou nábojem o plošné hustotě s- = -P (obr. 1.37).
Mějme nyní nekonečnou rovinnou polarizovanou vrstvu s konstantním vektorem polarizace P kolmým k rovinám ohraničujícím vrstvu. Analogicky jako v případě válce zjišťujeme, že výsledné elektrostatické pole takové vrstvy v celém prostoru (včetně objemu vrstvy) s výjimkou bodů na hraničních rovinách bude ekvivalentní poli dvojice rovin nabitých náboji s plošnými hustotami s+ = P a s- = -P (obr. 1.38). Takové pole jsme již zkoumali v příkladu 1.2.9c. Z výsledku plyne, že elektrostatické pole polarizované vrstvy je v prostoru mimo vrstvu nulové, uvnitř vrstvy homogenní, přičemž vektor Ep míří od kladně nabité podstavy k záporně nabité, kdežto vektor polarizace P naopak. Platí tedy
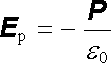 . . |
(1.180) |


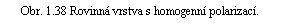
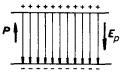
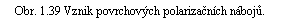

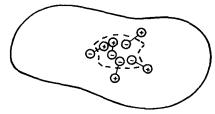
Situaci si můžeme též názorně představit tak, že kladné a záporné náboje dipólu se v objemu vrstvy vzájemně vykompenzují a uplatní se pouze kladné náboje dipólů tvořících horní hraniční rovinu a záporné náboje dipólů tvořících dolní hraniční rovinu (obr. 1.39).
Zatím jsme uvažovali pouze případ P = konst, tedy homogenní polarizaci. Pokud by v některém bodě prostoru platilo div P ^1 0, projevila by se tato skutečnost vznikem objemového náboje s hustotou, viz vztahy (1.168) . Názorně si můžeme tuto situaci představit pomocí modelu znázorněném na obr. 1.40.
Mějme objem kulového tvaru s poloměrem R spojitě zaplněný bodovými elektrickými dipóly s konstantní polarizací. Osu z vedeme středem koule souhlasně s vektorem polarizace P. Podle výrazů (1.168) a (1.169) bude elektrostatické pole vytvářené takovou polarizovanou koulí totožné s polem plošně nabité kulové slupky s proměnnou plošnou hustotou náboje
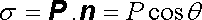 |
(1.181) |
(q je úhel mezi vektorem polarizace a normálou ke kulové ploše).
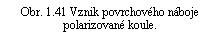

K takovému rozložení plošného náboje na povrchu koule můžeme dojít i jinak. Mějme dvě objemově nabité koule poloměru R s opačnými náboji Q- < 0, Q+ > 0 a hustotami r-, r+, jejichž středy jsou vzájemně nepatrně posunuty ve směru osy z o l << R. Nevykompenzované náboje na povrchu vytvoří přibližně plošné uspořádání s hustotou s = r l cos q, jak se lze snadno přesvědčit z obr. 1.41. Zde s = r DR, z trojúhelníku OO'A o stranách l, R, R - DR pomocí kosinové věty najdeme DR = l cos q . Velikost polarizace odpovídá tedy P = r l.
Jak víme, chová se rovnoměrně nabitá koule navenek tak, jako kdyby celý její náboj Q byl soustředěn v centru. Podle provedené úvahy se bude tedy rovnoměrně polarizovaná koule chovat navenek tak, jako kdyby v jejím centru byl umístěn bodový elektrický dipól o momentu
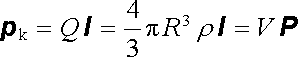 . . |
(1.182) |
Potenciál vně koule bude tedy dán vztahem (1.124) . Potenciál na povrchu polarizované koule bude pak roven
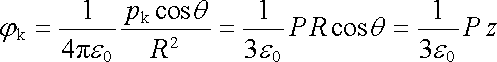 |
(1.183) |
a musí zůstat při přechodu přes povrch spojitým.
Uvnitř polarizované koule, kde hustota nábojů r = 0, musí být splněna Laplaceova rovnice (1.86) spolu s hraniční podmínkou j = jk. Potenciál tvaru (1.183) , přímo úměrný souřadnici z, Laplaceovu rovnici splňuje pro libovolné z, neboť všechny jeho druhé parciální rovnice jsou rovny nule. Jak však uvidíme v článku 1.4.4, je hraniční podmínkou určeno řešení Laplaceovy rovnice jednoznačně (srov. též příklad 1.4.7c). Vzorec (1.183) tedy udává potenciál v celém objemu koule. Pro pole uvnitř koule máme
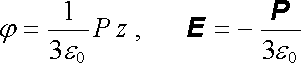 . . |
(1.184) |
Získaný výsledek můžeme porovnat s výrazem pro pole uvnitř polarizované vrstvy (1.180) : polarizovaná koule vytváří navenek elektrostatické pole ekvivalentní s polem elektrického dipólu umístěného v jejím středu, uvnitř je její elektrostatické pole homogenní, orientované opačně k vektoru polarizace a třikrát slabší než pole rovinné vrstvy o téže polarizaci.

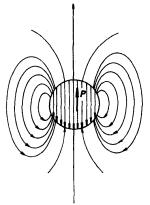
Snadno ověříme, že při přechodu povrchem koule zůstává tečná složka intenzity elektrického pole Et = -(P/3e0) sinq spojitá, zatímco normálová složka se mění skokem z hodnoty Eni = -(P/3e0) cosq uvnitř koule na Ene = (2P/3e0) cosq vně koule, tedy o veličinu P/3e0 cosq v souladu se vztahem (1.80) . Siločáry pole polarizované koule jsou znázorněny na obr. 1.42.