Uvažujme soustavu statických bodových nábojů Q1 až QN ve vakuu. Silové působení na další náboj Q je dáno vztahem (1.5) a lze je vyjádřit ve tvaru
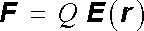 , , |
(1.32) |
kde
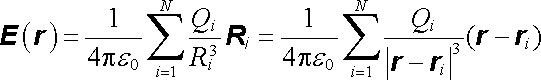 . . |
(1.33) |
Veličina E(r), kterou jsme formálně zavedli vztahy (1.32) a (1.33) , představuje vektorové pole, nazývá se intenzitou elektrostatického pole a je to vlastně síla, která působí v daném bodě na jednotkový kladný elektrický náboj. Vektor E je definován v každém bodě prostoru s výjimkou těch, v nichž se nacházejí náboje Qi (pro ně Ri = "ir - ri"i = 0). Tato potíž je důsledkem předpokladu o bodovém, diskrétním charakteru nábojů. V článku 1.2.4 uvidíme, že pro náboje spojitě rozložené v prostoru lze definovat intenzitu pole, která má smysl i v bodech s nenulovou hustotou náboje.
Zavedením intenzity elektrostatického pole jsme rozdělili problém silového působení mezi náboji do dvou kroků. Za prvé jsme bodu r přiřadili určitou hodnotu veličiny E(r) (intenzity pole) podmíněnou a určenou přítomností nábojů Q1 až QN v bodech r1 až rN. Za druhé jsme vyjádřili sílu působící na náboj Q umístěný v bodě r jako součin tohoto náboje a intenzity pole v daném bodě. Intenzita pole byla tak zavedena čistě formálně jako vektorové pole v matematickém smyslu. Tento postup je výhodný zejména při vyšetřování elektrostatického působení vodičů nebo v látkovém prostředí, kde není možno sledovat konkrétní rozložení nábojů v prostoru.
Elektrostatické pole reprezentované svojí intenzitou (pro soustavu bodových nábojů vyjádřenou vztahem (1.33) ), má některé pozoruhodné rysy, které zůstávají v platnosti i pro jiné obecnější typy polí. Je to především sama skutečnost, že síla působící na náboj v kterémkoliv bodě prostoru je úměrná hodnotě tohoto náboje. Druhá, ještě pozoruhodnější, je vlastnost nazývaná lokálnost pole. K určení síly působící na bodový náboj stačí znát pouze vektor intenzity pole v daném bodě a neuplatňuje se zde vliv okolí.
Znalost rozložení a hodnot nábojů vytvářejících elektrostatické pole a znalost intenzity pole jako funkce prostorových souřadnic jsou ekvivalentní. Vše, co lze vyjádřit pomocí poloh a hodnot nábojů, lze vyjádřit i pomocí intenzity pole; druhý způsob je přitom elegantnější a mnohem pohodlnější. Díky tomuto dualismu v možnosti popisu vzniká otázka, zda je třeba za prvotní fyzikální realitu považovat náboje či pole. Odpověď na tuto principiální otázku má dva pohledy. Tím, že jsme výraz pro sílu působící na náboj Q upravili na tvar (1.32) a zavedli intenzitu elektrostatického pole, jsme nikterak neovlivnili fyzikální obsah. Zatímco elektrický náboj a jeho silové účinky na jiné náboje jsou experimentálně prokázány, neexistuje žádný elektrostatický experiment, který by dokazoval existenci elektrostatického pole jako reálné fyzikální substance.
Na druhé straně však v kapitole 5, ve které budeme studovat vlastnosti nestacionárního elektromagnetického pole, uvidíme, že toto pole nemusí být vázáno na náboje, má vlastní hybnost a energii, která se může šířit prostorem, a řadu dalších reálných vlastností. Nestacionární elektromagnetické pole je jednou z forem hmoty, stejně reálnou jako látka. Makroskopické elektrostatické pole je pak jeho speciálním případem v situaci, kdy nositelé náboje v dané soustavě souřadnic nekonají makroskopický pohyb. Intenzitu pole ve smyslu vztahu (1.32) je třeba považovat za časovou a prostorovou střední hodnotu polí, která jsou v daném místě buzena jednotlivými mikroskopickými nositeli náboje. V tomto smyslu je elektrostatické pole fyzikálně reálným, adekvátním popisem elektromagnetické interakce v uvedené situaci.
Jednotku pro intenzitu elektrostatického pole lze odvodit z definičního vztahu (1.32) jako N.C-1. V mezinárodní soustavě jednotek je však jednotka intenzity elektrostatického pole odvozena od jednotky potenciálu volt (V) - viz odstavec 1.2.3. Pro intenzitu pole pak plyne jednotka V.m-1; obě jednotky jsou však ekvivalentní.
Na základě principu superpozice lze intenzitu pole vyjádřenou vztahem (1.33) chápat jako vektorový součet intenzit vytvořených v daném bodě r jednotlivými náboji Q1 až QN. Lze tedy psát
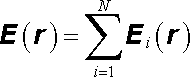 , , |
(1.34) |
kde
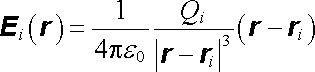 . . |
(1.35) |
Speciálně intenzita elektrostatického pole jediného bodového náboje Q umístěného v počátku soustavy souřadnic je dána vztahem
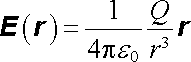 . . |
(1.36) |
Velikost intenzity elektrostatického pole bodového náboje ubývá tedy se čtvercem vzdálenosti.
Pro získání představy o průběhu pole dané soustavy nábojů je výhodné jeho grafické znázornění. K tomu účelu se nejčastěji užívá pojmu siločáry. Siločára je definována v bodech s nenulovou intenzitou pole jako orientovaná křivka mající tu vlastnost, že vektor intenzity v daném jejím bodě leží ve směru tečny, přičemž orientace vektoru intenzity souhlasí se směrem orientace křivky. Siločáry vždy vycházejí z kladných nábojů a vstupují do nábojů záporných; mohou též počínat a končit v nekonečnu. Protože vektor intenzity pole je v každém bodě definován jednoznačně, nemohou se siločáry vzájemně protínat. Hustotou siločar je možné vyjádřit velikost intenzity pole v dané části prostoru, podobně jako lze na mapě vyjádřit příkrost svahu hustotou vrstevnic. Pro získání názoru o průběhu pole obvykle stačí zobrazit soustavu siločar v některých význačných rovinách symetrie soustavy.
Na obrázku 1.9 je uvedeno několik příkladů. Obrázek 1.9a (1.9b) zobrazuje pole izolovaného kladného (záporného) bodového náboje v rovině procházející tímto nábojem. Na obrázku 1.9c vidíme pole dvojice bodových nábojů téže velikosti a opačného znaménka (takzvaný elektrický dipól) v rovině, v níž oba náboje leží. Podobně na obr. 1.9d je znázorněno analogickým způsobem pole dvojice kladných bodových nábojů téže velikosti. Konečně obr. 1.9e zobrazuje elektrostatické pole čtveřice bodových nábojů stejné velikosti umístěných ve vrcholech čtverce tak, že náboje stejného znamení leží na úhlopříčných vrcholech. Útvar uvedeného typu představuje takzvaný elektrický kvadrupól. Celkový náboj kvadrupólu je, podobně jako u elektrického dipólu, nulový. Jak uvidíme v oddílu 1.3, elektrický dipól a kvadrupól představují první členy řady takzvaných elektrických multipólů, které mají velký význam při aproximativním popisu elektrostatických polí nabitých těles s obecným rozložením nábojů.
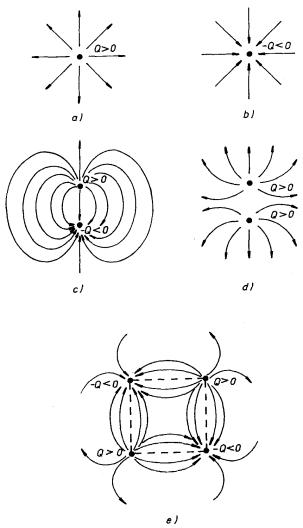
Obr. 1.9 Znázornění elektrického pole siločarami: a) kladného bodového náboje, b) záporného bodového náboje, c) konečného elektrického dipólu, d) soustavy dvou kladných bodových nábojů, e) konečného elektrického kvadrupólu.
Zavedeme nyní důležitý pojem toku intenzity elektrostatického pole. Pro názornost se přitom obrátíme k hydrodynamické analogii. Uvažujme proudící kapalinu.
Ptáme se, jaké její množství proteče danou plochou S za jednotku času. K řešení této úlohy zřejmě stačí znát rychlost kapaliny v(r) v každém bodě plochy S, tedy tzv. pole rychlostí. Ve speciálním případu podle obr. 1.10a, kdy plocha S je rovinná a rychlost kapaliny v ve všech jejích bodech je konstantní, platí pro hledaný průtok kapaliny F zřejmě
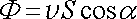 . . |
(1.37) |
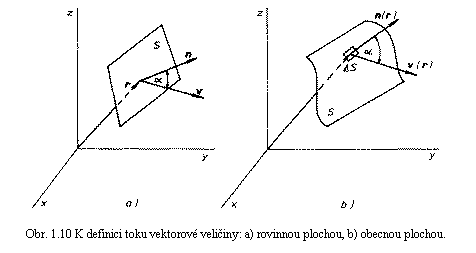
Jestliže je rovinná plocha S orientována, tj. je-li rozhodnuto, která ze dvou možných orientací vektoru normály je kladná, je možné zapsat výraz (1.37) ve vektorovém tvaru. Orientaci ohraničené rovinné plochy můžeme stanovit například tak, že rozhodneme, který z možných dvou směrů oběhu po její hranici je kladný, a požadujeme, aby kladný směr vektoru normály spolu se zvoleným kladným oběhem tvořily pravotočivou soustavu. Označíme-li jednotkový kladný vektor normály jako n a položíme-li vektor plochy S = Sn, můžeme (1.37) zapsat ve tvaru skalárního součinu
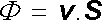 . . |
(1.38) |
V obecném případu podle obr. 1.10b, kdy má plocha S libovolný tvar a vektor rychlosti je funkcí polohy, nemůžeme definovat směr normály platný pro plochu S jako celek. Tok F však můžeme vypočítat jako součet toků DFi , přes dostatečně malé plošky DSi , které je možno s požadovanou přesností považovat za rovinné a jejichž sjednocení zcela vyplní plochu S. Pro každou plošku DSi lze alespoň přibližně zavést kladný jednotkový vektor normály ni a psát DSi = DSini, takže DFi = v.DSi. Z uvedené úvahy je patrné, jak je třeba zobecnit definici toku vektorového pole obecnou plochou, aby si tento pojem zachoval svůj fyzikální smysl. Tok intenzity elektrostatického pole budeme definovat jako plošný integrál
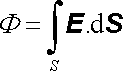 . . |
(1.39) |
Pro tok malou ploškou DS máme
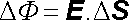 . . |
(1.40) |
Má-li vektor E směr kladné normály k plošce DS, bude tok touto ploškou maximální a můžeme psát
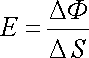 . . |
(1.41) |
Vidíme, že vektor intenzity elektrostatického pole můžeme považovat za vektor hustoty toku intenzity tohoto pole (srov. analogický vztah mezi proudem a hustotou proudu - odst. 3.1.1). Je zřejmé, že jednotkou toku intenzity elektrostatického pole bude volt metr (V. m).
Této okolnosti se využívá při normování počtu siločar procházejících kolmo danou plochou. Můžeme totiž požadovat, aby počet takových siločar připadajících na jednotku plochy byl právě roven velikosti vektoru intenzity elektrostatického pole.
Určíme nyní počet siločar vycházejících z kladného bodového náboje Q umístěného v počátku souřadnic. Jak víme, vycházejí siločáry z tohoto náboje radiálně a jsou rozloženy sféricky symetricky. Obklopíme náboj Q koncentrickou kulovou plochou poloměru r. Celkový počet siločar vycházejících z náboje Q je N = F. Počet siločar ve vzdálenosti r připadající na jednotku plochy přirovnáme velikosti vektoru E (1.36)
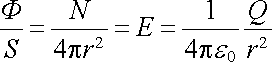 . . |
(1.42) |
Odtud dostáváme
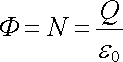 . . |
(1.43) |
Počet siločar vycházejících z bodového náboje a velikost tohoto náboje jsou tedy vázány vztahem úměrnosti. Tato skutečnost má závažný význam. Později uvidíme, že i při pohybu náboje zůstává jeho velikost a počet siločar s ním spojených neměnný.[4]
Zjistili jsme, že tok intenzity elektrostatického pole uzavřenou kulovou plochou, v jejímž středu je umístěn náboj Q, je roven (1.43) . Ukážeme nyní, že tento vztah platí obecně pro uzavřenou plochu libovolného tvaru a celkový náboj v prostoru ohraničeném touto plochou.
Uvažujme opět soustavu statických bodových nábojů Q1 až QN. Zvolme uzavřenou plochu S, v níž jsou obsaženy některé z těchto nábojů; nechť žádný z nich na ní neleží. Uzavřenou plochu budeme orientovat tak, že vektor normály n mířící na její vnější stranu budeme považovat za kladný. Najdeme celkový tok intenzity elektrického pole F touto plochou. S ohledem na princip superpozice a aditivnost toku můžeme vyšetřovat příspěvek každého náboje zvlášť.
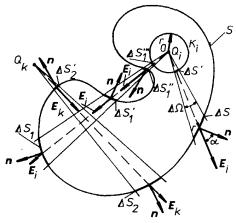
Nechť náboj Qi leží uvnitř prostoru
ohraničeného plochou S. Opišme kolem
něj kouli Ki o poloměru r0 a veďme kuželovou plochu o prostorovém vrcho-lovém úhlu DW (viz obr. 1.11). Tato plocha vytíná na kouli Ki malou plošku
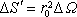 a na ploše S plošku DS = r2 DW /cos a. Platí
a na ploše S plošku DS = r2 DW /cos a. Platí
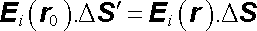 , , |
(1.44) |
neboť
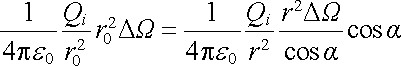 . . |
Tok intenzity
vzbuzené nábojem Qi, je
tedy stejný pro obě plošky DS, DSc.
Jak plyne z obrázku, nezmění se situace ani tehdy, protne-li kuželová plocha
plochu S několikrát. Toky všemi
ploškami
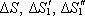 jsou v absolutní hodnotě stejné a rovné toku
příslušnou ploškou
jsou v absolutní hodnotě stejné a rovné toku
příslušnou ploškou
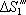 vytčenou na kouli. Tok ploškou
vytčenou na kouli. Tok ploškou
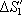 je však záporný, takže platí opět
je však záporný, takže platí opět
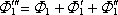 .
Tok Fi,
kterým náboj Qi
přispívá k celkovému toku plochou S,
je tedy roven toku vektoru Ei
kulovou plochou Ki
.
Tok Fi,
kterým náboj Qi
přispívá k celkovému toku plochou S,
je tedy roven toku vektoru Ei
kulovou plochou Ki
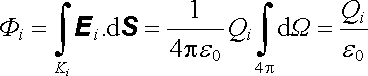 |
(1.45) |
v souladu s (1.43) .
Na základě analogických úvah zjistíme, že náboje ležící vně plochy S nepřispívají k celkovému toku (viz příklad náboje Qk na obrázku). Použijeme-li nyní princip superpozice, můžeme formulovat Gaussův zákon elektrostatiky pro soustavu bodových nábojů:
Celkový tok F intenzity elektrostatického pole soustavy bodových nábojů libovolnou uzavřenou plochou S je roven celkovému náboji Qc uzavřenému uvnitř této plochy dělenému konstantou e0.
Platí
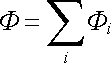 , , |
(1.46) |
přičemž index i
probíhá pouze náboje umístěné uvnitř plochy S.
Označíme-li celkový náboj uvnitř této plochy jako
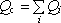 můžeme Gaussův zákon zapsat ve tvaru
můžeme Gaussův zákon zapsat ve tvaru
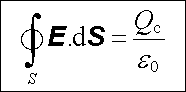 |
(1.47) |
(značka
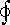 vyjadřuje, že plošný integrál je brán přes
uzavřenou plochu).
vyjadřuje, že plošný integrál je brán přes
uzavřenou plochu).
Gaussův zákon hraje v nauce o elektřině fundamentální úlohu. V dalším výkladu uvidíme, že platí pro libovolné elektrostatické pole a je možno jej zobecnit i na případ pohybujících se nábojů. Jak je patrno z průběhu odvození, je Gaussův zákon přímým důsledkem Coulombova zákona, resp. zákona převrácených čtverců a principu superpozice. Přitom Gaussův zákon a z něj plynoucí důsledky je možno ověřit dalšími experimenty, např. s rozložením nábojů na vodičích, a tím nepřímo dokázat i platnost Coulombova zákona (viz článek 1.4.2). Při odvozování Gaussova zákona jsme nevyužili předpokladu o kulové symetrii pole bodového náboje a v tomto smyslu je Gaussův zákon obecnější než zákon Coulombův. Doplníme-li k platnosti Gaussova zákona předpoklad kulové symetrie, dostaneme snadno vztah (1.36) a přes (1.32) Coulombův zákon.
Zmínili jsme se o tom, že silové působení soustavy statických bodových nábojů Q1 až QN na náboj Q umístěný v bodě r lze popsat zavedením vektorového pole E(r) daného výrazem (1.33) . V bodech r = ri není vektorová funkce E(r) definována, má zde singularitu řádu 1/x2. Uvažme nyní skalární funkci (skalární pole) j(r) definovanou vztahem
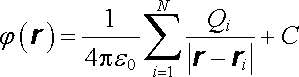 , , |
(1.48) |
kde C je libovolná konstanta. Tato funkce má rovněž singularity v bodech r = ri (řádu 1/x); všude jinde má parciální derivace všech řádů. Pro případ jednoho bodového náboje umístěného v počátku souřadnic definujeme podle (1.48)
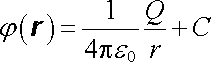 . . |
(1.49) |
Vypočítáme-li nyní parciální derivace prvního řádu funkce j(r) dané vztahem (1.48) , popř. (1.49) , zjistíme, že pro E(r) dané vztahem (1.33) , popř. (1.36) , platí
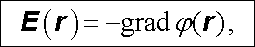 |
(1.50) |
kde symbol grad j značí vektor grad j = (Pj /Px, Pj /Py, Pj /Pz) nazývaný gradientem funkce j (podrobněji viz Dodatek l).
Skalární funkci j(r) nazýváme potenciálem elektrostatického pole. Vzhledem k platnosti vztahu (1.50) je možné potenciál použít k popisu elektrostatického pole soustavy bodových nábojů stejně tak jako intenzitu pole E(r); popis pomocí potenciálu je dokonce jednodušší (je to skalár a při sčítání potenciálů se nemusíme starat o směr této veličiny). Přítomnost volitelné konstanty C v definičním vztahu (1.48) pro potenciál ukazuje na to, že potenciál není definován jednoznačně. Jak uvidíme, tato skutečnost nemá však fyzikální důležitost.
Existence potenciálu obecného vektorového pole není samozřejmá a pole, která je možno vyjádřit vztahem (1.50) , nazýváme potenciálními. Možnost popisu elektrostatického pole soustavy bodových nábojů pomocí potenciálu jsme dokázali tím, že jsme zkonstruovali funkci (1.48) vyhovující vztahu (1.50) . Vzniká ovšem otázka, jaký má potenciál fyzikální význam a jakou vlastnost elektrostatického pole vyjadřuje.
V uvažovaném poli soustavy bodových nábojů
zvolme pevný bod r0
různý od všech bodů r1
až rN ve kterých sídlí bodové
náboje. Zvolme dále libovolný bod r téže vlastnosti a oba body spojme křivkou l,
která je orientována od bodu r0 k r a která
neprochází žádným z bodů r0 až rN. Bude nás zajímat práce
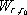 kterou musí vnější síly vykonat, má-li být
bodový náboj Q přenesen z výchozího
bodu r0
po křivce l do bodu r. Platí (srov. vztah
(1.23)
)
kterou musí vnější síly vykonat, má-li být
bodový náboj Q přenesen z výchozího
bodu r0
po křivce l do bodu r. Platí (srov. vztah
(1.23)
)
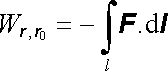 , , |
(1.51) |
kde F značí sílu podle (1.32) , která musí být při přenášení náboje Q překonávána. Využitím rovnice (1.50) dostaneme dále
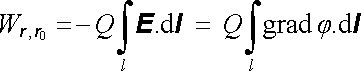 . . |
(1.52) |
Výraz
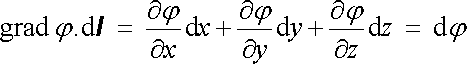 |
(1.53) |
však představuje totální diferenciál potenciálu. Odtud vyplývá důležitý výsledek
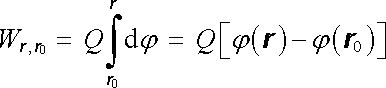 . . |
(1.54) |
Práce
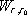 závisí jen na potenciálu koncových bodů dráhy
l a nezávisí na jejím průběhu. Má
tedy význam potenciální energie náboje Q
v bodě r
vzhledem k bodu r0.
závisí jen na potenciálu koncových bodů dráhy
l a nezávisí na jejím průběhu. Má
tedy význam potenciální energie náboje Q
v bodě r
vzhledem k bodu r0.
Potenciál elektrostatického pole v daném bodě zde tedy představuje potenciální energii vztaženou k jednotkovému náboji. Je určen vzhledem k referen-čnímu bodu, jehož potenciál i polohu můžeme volit libovolně. Pokud jsou všechny náboje rozloženy v konečné části prostoru, volíme obvykle referenční bod v nekonečnu a klademe tam potenciál roven nule. Potom podle rovnic (1.50) a (1.53) máme
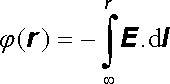 . . |
(1.55) |
Fyzikální smysl má tedy jen rozdíl potenciálů ve dvou bodech r1, r2, který můžeme měřit, tedy
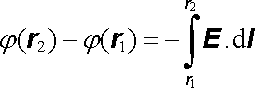 . . |
(1.56) |
Práci, kterou vykoná elektrostatické pole při přemisťování bodového jednot-kového kladného náboje z bodu r1 do bodu r2, nazýváme napětím mezi těmito body:
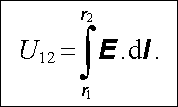 |
(1.57) |
Napětí je tedy rovno záporně vzatému rozdílu potenciálů a je kladné, má-li výchozí bod vyšší potenciál než bod koncový. Elektrostatické pole vykoná v takovém případě při přemisťování kladného náboje kladnou práci A = Q U12.
Ze vztahu (1.54) snadno stanovíme jednotku pro měření potenciálu, resp. napětí. V Mezinárodní soustavě je jí volt (V). Mezi dvěma body je napětí jednoho voltu, jestliže elektrické pole při přenesení náboje jednoho coulombu vykoná práci jednoho joulu. Ze vztahu (1.57) pak plyne jednotka intenzity elektrostatického pole V.m-1.
Nyní použijeme potenciál k vyjádření potenciální energie soustavy bodových nábojů, kterou jsme odvodili v článku 1.1.5. Mějme nejprve dvojici nábojů Q1, Q2 ve vzájemné vzdálenosti R12. Náboj Q1 vyvolává v bodě, kde je umístěn druhý náboj Q2, potenciál j2 daný vztahem tvaru (1.49) s C = 0. Analogicky náboj Q2 vyvolává potenciál j1 v bodě, v němž je umístěn náboj Q1. Potenciální energii soustavy těchto dvou nábojů můžeme pak zapsat jako
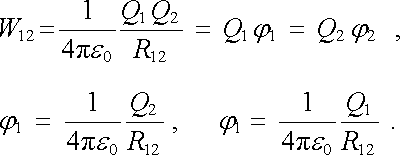 |
(1.58) |
Víme, že tato energie nezávisí na tom, po jaké trajektorii se náboj Q1(Q2) přibližoval z nekonečna do bodu o vzdálenosti R12 od náboje Q2(Q1).
Mějme nyní soustavu nábojů Q1 až QN. Potenciální energii náboje Qj v poli ostatních nábojů Qi^1j můžeme vyjádřit pomocí potenciálu s uvážením principu superpozice jako
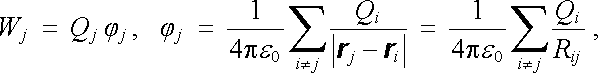 |
(1.59) |
takže výsledná potenciální energie soustavy (1.25) bude mít tvar
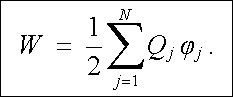 |
(1.60) |
Ze skutečnosti, že práce vykonaná při přenesení náboje mezi dvěma body v elektrostatickém poli nezávisí na trajektorii, přímo vyplývá, že práce vykonaná po uzavřené křivce je vždy rovna nule. Přenášíme-li po takové trajektorii jednotkový náboj, na nějž působí síla rovná intenzitě pole E, dostaneme obecný integrální vztah
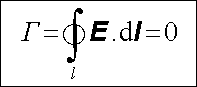 |
(1.61) |
(symbol
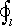 vyjadřuje, že integrál je brán podél uzavřené
křivky l; nazýváme ho cirkulace
vektoru E
podél této křivky). Podle Stokesovy věty vektorové analýzy (viz D 1.45)
vyjadřuje, že integrál je brán podél uzavřené
křivky l; nazýváme ho cirkulace
vektoru E
podél této křivky). Podle Stokesovy věty vektorové analýzy (viz D 1.45)
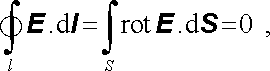 |
(1.62) |
kde S je libovolná plocha, která má za svou hranici křivku l. Připomeňme, že vektorové pole rot E nazývané rotace E je v kartézských souřadnicích definováno jako
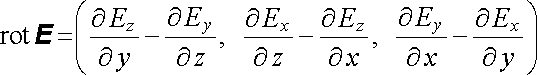 |
(viz Dodatek l).
Vzhledem k tomu, že křivka l je libovolná, bude vztah (1.62) platit i pro diferenciálně malou plošku dS. Pak dostaneme diferenciální obdobu vztahu (1.61) jako
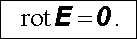 |
(1.63) |
Mohli jsme též použít identity vektorové analýzy (viz D 1.64)
 |
(1.64) |
Rovnice (1.61) , resp. (1.63) jsou přímým důsledkem existence potenciálu. Použitý postup lze ovšem i obrátit a z platnosti těchto rovnic existenci potenciálu vyvodit. Vztah (1.61) , resp. (1.63) platí tedy právě tehdy, existuje-li skalární funkce splňující podmínku (1.50) . Znamená to, že elektrostatické pole soustavy bodových nábojů je potenciální a konzervativní (energie náboje se po návratu do výchozího bodu zachová).
Pro grafické znázornění elektrostatického pole lze vedle siločar použít též tzv. ekvipotenciálnich ploch. Jsou definovány jako geometrické místo bodů, v nichž má potenciál předepsanou konstantní hodnotu ji. Snadno lze dokázat, že siločáry jsou vždy k ekvipotenciálním plochám kolmé. Diferencujeme-li totiž rovnici
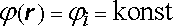 , , |
(1.65) |
dostaneme
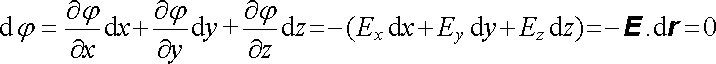 . . |
(1.66) |
Jelikož vektor dr = (dx, dy, dz) leží v rovině tečné k ekvipotenciální ploše, je dokazované tvrzení zřejmé. Pro posouzení průběhu pole opět stačí vyšetřovat pouze průsečnice ekvipotenciálních ploch s některými význačnými rovinami symetrie soustavy.
Dosud jsme se zabývali elektrostatickým polem vytvářeným soustavou bodových nábojů. Nyní přejdeme k obecnému rozložení elektrických nábojů, které jsme popsali v článku 1.1.4 pomocí pojmu objemové (plošné, lineární) hustoty náboje. Hustotu náboje budeme pokládat za známou funkci polohového vektoru, nezávislou na čase. Nebudeme se přitom starat o fyzikální vlastnosti objektů nesoucích tyto náboje, ani nebudeme brát v úvahu jejich vliv na vyšetřované elektrostatické pole. Jinými slovy řečeno, budeme předpokládat určité známé rozložení nábojů v prostoru a jimi vytvořené elektrostatické pole budeme považovat za pole ve vakuu.

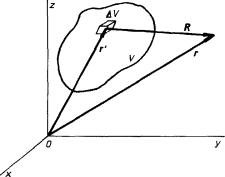
Uvažujme náboj Q objemově rozložený v oblasti o objemu V s hustotou r (rc) (obr. 1.12). Pro přibližný výpočet intenzity pole vzbuzeného tímto nábojem v libovolném bodě r ležícím mimo oblast V použijeme Coulombův zákon a princip superpozice; rozdíl vektorů r - rc označíme jako R. Nejdříve určíme příspěvek náboje DQ rozloženého v malém objemu DV, který obsahuje bod rc. Zvolíme-li tento objem dostatečně malý, můžeme náboj DQ B r (rc)DV vzhledem ke vzdálenosti k bodu r považovat s potřebnou přesností za bodový. Jeho příspěvek DE(rc) k celkové intenzitě pole můžeme podle (1.35) vyjádřit ve tvaru
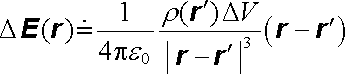 . . |
(1.67) |
Analogicky pro příspěvek Dj (r) k potenciálu v daném bodě dostaneme podle (1.49) (klademe C = 0)
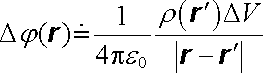 . . |
(1.68) |
Celkovou intenzitu pole E(r), resp. potenciál j(r) můžeme podle principu superpozice s požadovanou přesností vyjádřit jako součet výrazů typu (1.67) , popř. (1.68) . Sčítání provádíme přes všechny elementární objemy, jejichž sjednocení zcela vyplní uvažovanou oblast V. Přesnost vyjádření bude samozřejmě tím větší, čím jemnější dělení oblasti V bude zvoleno.
Podle právě provedené úvahy lze očekávat, že objemové integrály (přes rc)
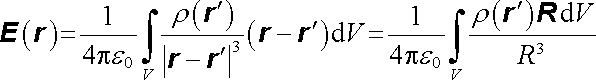 , , |
(1.69a) |
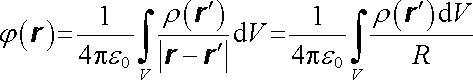 |
(1.70a) |
budou přesně vyjadřovat hledanou intenzitu pole a potenciál ve všech bodech r mimo objem V. Zmíněnou úvahu není ovšem možno ve smyslu formální logiky považovat za důkaz těchto vztahů. Kdybychom požadovali, aby naše teorie byla formálně konzistentní, museli bychom jejich platnost vedle Coulombova zákona rovněž postulovat. Fyzikální smysl výrazů (1.69a) a (1.33) je týž, rozdíl je pouze ve způsobu nazírání. Elektrostatické pole reálného tělesa nesoucího náboj je možno buď podle (1.33) vyjádřit jako pole vhodně zvolených diskrétně rozložených bodových nábojů, nebo podle (1.69a) jako pole spojitě rozloženého náboje.
Intenzita pole a potenciál vyjádřené vztahy (1.69a) a (1.70a) vyhovují definiční podmínce potenciálu (1.50) :
(eq0089). (1.71)
Funkce r popisující reálná rozložení náboje takovou záměnu pořadí derivování (podle r ) a integrování (podle rc) vždy umožňuje. Stačí tedy určit pouze jednu z funkcí E(r), j(r) a druhou najít pomocí vztahu (1.50) .
Všechny úvahy, které jsme dosud prováděli pro prostorově rozložené náboje můžeme reprodukovat i pro náboje rozložené plošně a lineárně. Je-li náboj Q rozložen na ploše S s plošnou hustotou s(rc), je možné intenzitu a potenciál jím vytvořeného elektrostatického pole v libovolném bodě neležícím na této ploše vyjádřit ve tvaru plošných integrálů
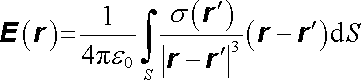 , , |
(1.69b) |
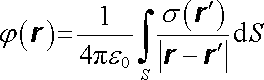 . . |
(1.70b) |
Analogicky, je-li náboj Q rozložen na křivce l s lineární hustotou t(rc), je možno intenzitu a potenciál jím vytvořeného elektrostatického pole v libovolném bodě neležícím na této křivce vyjádřit ve tvaru křivkových integrálů
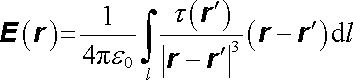 , , |
(1.69c) |
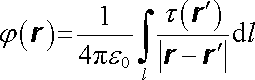 . . |
(1.70c) |
Na základě toho, co bylo dosud řečeno, umíme tedy obecně vyjádřit intenzitu a potenciál elektrostatického pole ve všech bodech, v nichž neleží bodové náboje a v nichž je hustota nábojů nulová. Vzniká nyní otázka, zda je možné rozšířit pojem elektrostatického pole také na body s nenulovou hustotou náboje. Pro vyřešení tohoto problému je třeba vyšetřit, za jakých podmínek mají výrazy (1.69) a (1.70) smysl i v uvedených bodech. Problém spočívá v tom, že jestliže bod r leží v oblasti, přes níž se integruje, může integrační proměnná nabývat hodnoty rc = r. Integrovaná funkce roste při rc (R) r do nekonečna. Mají-li být intenzita pole, resp. potenciál v tomto bodě konečné, budou mít charakter nevlastních hodnot příslušných integrálů. Existence těchto nevlastních hodnot pak závisí na průběhu hustoty náboje, tj. na tvaru funkcí r (rc), s(rc), t(rc).
Detailní rozbor této problematiky je záležitostí teorie elektromagnetického pole, resp. teorie potenciálu (viz např. [3]). Uvedeme proto jen hlavní závěry týkající se v praxi důležitých případů. Omezíme se přitom pouze na objemové a plošné rozložení nábojů. O funkcích r(rc) a s(rc) vyjadřujících objemovou a plošnou hustotu náboje budeme prostě předpokládat, že jsou ve všech vnitřních bodech uvažované oblasti konečné a dostatečně hladké.
O elektrostatickém poli prostorově rozložených nábojů lze za uvedených předpokladů říci:
1. Výraz (1.70a) vyjadřuje konečný potenciál ve všech bodech prostoru, tedy i v bodech oblasti V, kdy je hustota náboje r různá od nuly.
2. Tento potenciál je všude spojitý a má parciální derivace alespoň prvního řádu.
3. Výraz (1.69a) je roven -grad j ve všech bodech prostoru. Vyjadřuje tedy správně intenzitu pole i uvnitř oblasti V, kde je hustota náboje různá od nuly.
4. Intenzita pole daná vztahem (1.69a) je všude spojitá.
O elektrostatickém poli plošně rozložených nábojů platí za analogických podmínek:
1. Výraz (1.70b) vyjadřuje konečný potenciál ve všech bodech prostoru, tedy i v bodech plochy S, kde je plošná hustota náboje s různá od nuly.
2. Tento potenciál je všude spojitý a má parciální derivace alespoň prvního řádu ve všech bodech s výjimkou bodů plochy S.
3. Výraz (1.69b) je roven -grad j ve všech bodech s výjimkou bodů plochy S. Na této ploše nemá intenzita pole smysl.
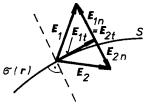
4. Intenzita pole daná vztahem (1.69b) je všude spojitá s výjimkou bodů plochy S. Při průchodu touto plochou zůstávají spojité pouze její tečné složky. Její normálové složky se mění skokem o hodnotu s /e0 . Platí tedy vztahy (viz obr. 1.13)
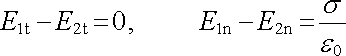 . . |
(1.72) |
Ke zdůvodnění těchto vztahů se vrátíme v článku 1.2.6.

S ohledem na princip superpozice lze očekávat, že Gaussův zákon formulovaný pro soustavu bodových nábojů rovnicí (1.47) bude platit také v případě spojitě rozložených nábojů. Abychom se o tom přesvědčili, museli bychom zkoumat výraz pro tok intenzity elektrostatického pole (1.39) a dosadit v něm za vektorovou funkci E(r) výrazy typu (1.69) . Aniž bychom platnost takové obecnější formulace Gaussova zákona exaktně zdůvodňovali, uvedeme přímo jeho znění:
Budiž dána libovolná uzavřená plocha S
ohraničující těleso objemu V a orientovaná tak, že kladný vektor normály
míří ven z tohoto tělesa. Nechť uvnitř této plochy je uzavřen náboj Qc, který může být tvořen jednak bodovými náboji, jednak náboji spojitě
rozloženými libovolným způsobem. Potom, existuje-li plošný integrál
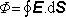 vyjadřující
tok intenzity elektrostatického pole touto plochou, platí
vyjadřující
tok intenzity elektrostatického pole touto plochou, platí
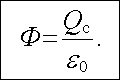 |
(1.73) |
Jak plyne z formulace Gaussova zákona, existuje pouze jediné omezení na volbu plochy S, a to aby přímo neprocházela takovými singularitami pole, které by znemožnily určit tok F. Toto omezení má však pouze teoretický význam, neboť v přírodě žádné singularity pole neexistují. Uvedené singularity mají svůj původ v tom, že k popisu pole používáme výhodných abstraktních pojmů jako bodový náboj, plošná hustota náboje apod. Kteroukoliv konkrétní skutečnou soustavu však můžeme s libovolnou přesností popsat objemovým rozložením nábojů tak, že pole je všude konečné a spojité.
Ve speciálním případu, kdy uvnitř plochy S jsou nejvýše objemově rozložené náboje, lze rovnici (1.73) vyjadřující Gaussův zákon v integrálním tvaru přepsat do tvaru diferenciálního. Náboj Qc můžeme totiž vyjádřit objemovým integrálem
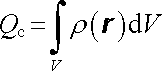 |
(1.74) |
(na rozdíl od integrálů (1.69) a (1.70) nyní integrujeme přes proměnnou r ).
Dostaneme tak
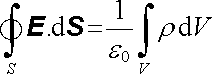 . . |
(1.75) |
Podle Gaussovy věty vektorové analýzy (viz Dodatek l, vztah (D 1.32)) lze však plošný integrál funkce E na levé straně (1.75) vyjádřit pomocí objemového integrálu funkce div E přes objem ohraničený plochou S. Platí tedy
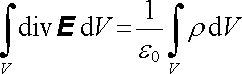 . . |
(1.76) |
Protože plocha S, a tudíž i objem V jsou voleny libovolně, musí poslední rovnice platit i pro diferenciálně malé objemy dV. To je možné pouze tehdy, jsou-li si identicky rovny integrované funkce. Musí proto platit v každém bodě
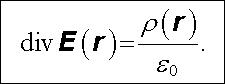 |
(1.77) |
Rovnice (1.77) představuje parciální diferenciální rovnici prvního řádu a vyjadřuje tutéž vlastnost elektrostatického pole jako Gaussův zákon (1.73) (a zahrnuje tedy v sobě i Coulombův zákon). Není však vázána na zadanou plochu či objem, a je to tedy Gaussův zákon v diferenciálním tvaru. V kartézských souřadnicích ji můžeme zapsat jako
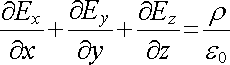 . . |
(1.78) |
Vzhledem ke geometrickému významu pojmu divergence (viz Dodatek l) vyjadřuje tato věta skutečnost, že náboje jsou zdrojem siločar elektrostatického pole. Je-li v nějakém bodě hustota náboje r, a tedy i divE kladná, znamená to, že siločáry z tohoto bodu vycházejí; naopak, jsou-li r a divE záporné, siločáry do takového bodu vstupují. Naproti tomu v daném bodě prostoru, v němž není elektrický náboj (r = 0), nelze vytvořit takovou konfiguraci elektrického pole, aby všechny okolní siločáry do tohoto bodu směřovaly. Odtud plyne tzv. Earnshawova věta, podle níž nelze elektrický náboj udržovat v prostoru ve stabilní rovnováze pouze silami elektrostatického pole (srov. příklad 1.1.6a).
Gaussův zákon v diferenciálním tvaru jsme odvodili pro případ objemově rozložených nábojů. Nyní budeme aplikovat Gaussův zákon (1.73) na případ plošně rozložených nábojů (obr. 1.14).

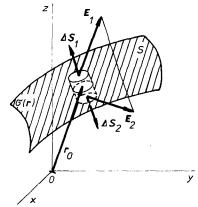
Mějme nabitou plochu S s plošnou hustotou náboje s a na ní bod r0. Obklopíme tento bod válcovou plochou tak, že osa válce bude kolmá k ploše S, obsah podstavy válce roven DS a dostatečně malý. Určíme tok intenzity elektrostatického pole touto válcovou plochou. K toku podstavami válce budou zřejmě přispívat pouze normálové složky pole E1n, E2n; vektory plošek obou podstav DS1, DS2 jsou přitom orientovány na opačné strany. Výšku válce můžeme učinit natolik malou, aby tok pláštěm byl zanedbatelný. Celkový tok válcovou plochou se pak zredukuje v limitě na F = E1.DS1 + E2.DS2 = (E1n - E2n) DS. Podle Gaussova zákona má být tento tok roven náboji uvnitř válcové plochy s DS dělenému e0:
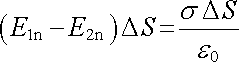 . . |
(1.79) |
Po vykrácení DS dostaneme druhou z podmínek (1.72)
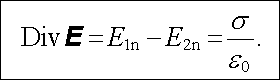 |
(1.80) |
Takzvaná plošná divergence DivE zavedená formálně vztahem (D 1.39), která se někdy používá, umožňuje vyjádřit podmínku pro normálové složky elektrostatického pole při průchodu danou plochou ve tvaru analogickém Gaussovu zákonu v diferenciálním tvaru (1.77) .
V předchozím textu
jsme zavedli potenciál elektrostatického pole vytvářeného soustavou bodových
nábojů, ukázali, že takové pole je konzervativní, a odvodili integrální
vztah
(1.61)
. Tento integrální vztah, a tedy i vlastnost konzervativnosti,
bude zřejmě platit i pro obecné elektrostatické pole buzené libovolně uspořádanými
náboji. Jediným požadavkem je, aby integrál
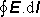 měl smysl, což je v reálné fyzikální situaci (podobně jako v případě Gaussova zákona)
vždy splněno.
měl smysl, což je v reálné fyzikální situaci (podobně jako v případě Gaussova zákona)
vždy splněno.
Dále jsme pomocí Stokesovy věty vektorové analýzy odvodili parciální diferenciální rovnici (1.63) . Použití Stokesovy věty je přesně vzato omezeno pouze na případ, když vektor intenzity pole E je spojitý a má spojité parciální derivace ve všech bodech křivky l a jí ohraničené plochy S. V případě bodových, lineárních a plošných nábojů (což jsou všechno fyzikální abstrakce) nebude tedy Stokesova věta obecně použitelná. Obecná definice operace rotace (viz Dodatek l, vztah (D 1.43)) však není závislá na volbě souřadnic, na existenci a na vlastnostech příslušných parciálních derivací. Takto definovaná veličina rot E má smysl i v bodech, kde jsou rozmístěny bodové lineární či plošné náboje a parciální diferenciální rovnice (1.63) nabývá obecnou platnost ve všech bodech prostoru pro libovolné elektrostatické pole.
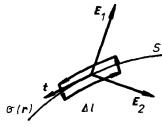
Dokažme nyní platnost prvního z hraničních vztahů (1.72) pro tečné složky elektrostatického pole (viz obr. 1.15). Mějme opět nabitou plochu S a veďme kolem uvažovaného bodu této plochy obdélníček tak, aby jeho delší strany Dl procházely rovnoběžně s libovolným tečným jednotkovým vektorem t po protějších stranách plochy S. K cirkulaci vektoru intenzity podél stran Dl obdélníčku budou zřejmě přispívat pouze tečné složky pole E1t, E2t. Strany kolmé k ploše S můžeme učinit tak krátkými, aby jejich příspěvek k cirkulaci byl zanedbatelný. Ze vztahu (1.61) v limitě dostáváme G = (E1.t - E2.t ) Dl = 0, a tedy
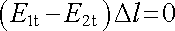 , , |
(1.81) |
a po vykrácení Dl máme první ze vztahů (l.72). Použijeme-li tzv. plošné rotace definované pomocí (D 1.52), můžeme psát analogicky k (1.63)
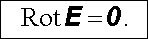 |
(1.82) |

Vraťme se nyní k obecnému případu, kdy rozložení nábojů můžeme popsat pomocí objemové hustoty náboje r(r). Vlastnosti elektrostatického pole jsou pak vyjádřeny parciálními diferenciálními rovnicemi
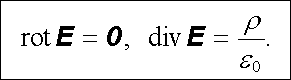 |
(1.83) |
Řešení této soustavy čtyř rovnic (jedné vektorové dvojice rovnic a jedné skalární dvojice rovnic) je usnadněno zavedením potenciálu. Možnost jeho zavedení plyne právě z první z rovnic (1.83) a přejdeme-li od vektoru E ke skalární funkci j vztahem (1.50) , bude tato první rovnice splněna automaticky. Zbývá pak řešit druhou z rovnic (1.83) . Využijeme přitom vztahu (D 1.56), jímž byl zaveden tzv. Laplaceův operátor. V kartézských souřadnicích máme
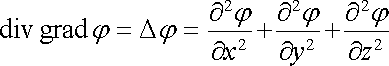 . . |
(1.84) |
Pro potenciál dostáváme tzv. Poissonovu rovnici
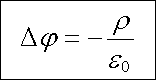 |
(1.85) |
platnou všude tam, kde platí Gaussův zákon v diferenciálním tvaru. V bodech, kde je objemová hustota nábojů nulová, redukuje se Poissonova rovnice na rovnici Laplaceovu
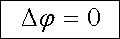 |
(1.86) |
nebo v kartézských souřadnicích
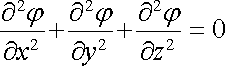 . . |
(1.86a) |
Poissonova a Laplaceova rovnice představují podmínky, kterým musí potenciál elektrostatického pole vždy vyhovovat. Ze známého rozložení nábojů umožňují určit potenciál (a tím i intenzitu pole) a naopak ze známého průběhu potenciálu dovolují určit soustavu nábojů tvořících zdroje tohoto potenciálu. Řešení těchto rovnic mají přitom určité obecné vlastnosti, které zkoumá matematická fyzika, a které usnadňují nalézt příslušné fyzikální řešení. Protože jde o parciální diferenciální rovnice, neurčují řešení jednoznačné. Abychom dostali jednoznačný fyzikální výsledek, musíme zadat ještě další, například tzv. hraniční podmínky.
Jednou ze zmíněných obecných vlastností potenciálu je to, že
elektrostatický potenciál nemůže mít lokální extrém v bodech, v nichž nesídlí
žádné náboje. Předpokládejme například, že uvažovaný potenciál má v bodě r0
lokální maximum. Pak jistě existuje kulová plocha K se středem v bodě r0, v jejíchž všech bodech má potenciál hodnotu menší než j(r0)
a vektor gradj míří dovnitř
objemu ohraničeného touto plochou. Intenzita pole E = -gradj
míří tudíž ven z plochy K, což
znamená, že
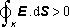 .
Tato podmínka může být s ohledem na Gaussův zákon splněna jen tehdy, je-li
uvnitř plochy K přítomen kladný náboj,
jehož siločáry směřují ven z plochy
K. Vidíme tedy, že řešení Laplaceovy
rovnice nemůže mít lokální extrém v žádném vnitřním bodě uvažované oblasti.
Řešení Poissonovy rovnice naopak takový extrém mít může, má-li hustota náboje v
uvažovaném bodě a jeho okolí vhodný průběh.
.
Tato podmínka může být s ohledem na Gaussův zákon splněna jen tehdy, je-li
uvnitř plochy K přítomen kladný náboj,
jehož siločáry směřují ven z plochy
K. Vidíme tedy, že řešení Laplaceovy
rovnice nemůže mít lokální extrém v žádném vnitřním bodě uvažované oblasti.
Řešení Poissonovy rovnice naopak takový extrém mít může, má-li hustota náboje v
uvažovaném bodě a jeho okolí vhodný průběh.
Nemožnost existence lokálního extrému v prázdném prostoru je přímo patrná i z tvaru Laplaceovy rovnice (1.86a) . V bodě extrému by musely být všechny první parciální derivace potenciálu nulové a všechny tři druhé parciální derivace buď kladné, nebo záporné, což rovnice (1.86a) vylučuje.
Nakonec vyjádříme ještě energii obecného elektrostatického pole. Viděli jsme, že interakční energie soustavy bodových nábojů může být vyjádřena pomocí potenciálu vztahem (1.60) . Zobecníme-li tento výsledek pro případ spojitě rozloženého náboje umístěného v konečnu, můžeme napsat
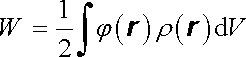 . . |
(1.87) |
Integrování přitom probíhá v celém prostoru. Použijeme-li Poissonovu rovnici, dostaneme
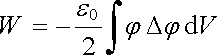 . . |
(1.88) |
Integrál na pravé straně (1.88) vzatý v konečném objemu V ohraničeném plochou S lze pomocí Greenovy věty vektorové analýzy (D 1.69) upravit na tvar
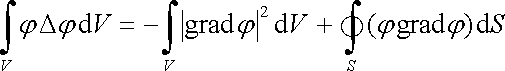 . . |
(1.89) |
Bude-li se nyní plocha S rozpínat do nekonečna, bude tok vektoru j grad j touto plochou konvergovat k nule (výraz j grad j bude klesat jako 1/r3, element plochy poroste jako r2 ). Objemové integrování se tak rozprostře po celém prostoru a my dostaneme
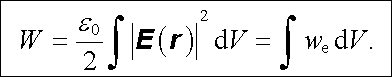 |
(1.90) |
Výsledek lze interpretovat tak, že elektrostatické pole je charakterizováno objemovou hustotou energie
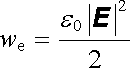 |
(1.91) |
a interakční energii obecně rozloženého náboje můžeme najít zintegrováním této hustoty v celém objemu, kde je elektrostatické pole nenulové.
Je užitečné si ověřit, že výraz (1.91) má skutečně fyzikální rozměr objemové hustoty energie J.m-3. Fyzikální význam hustoty energie we ovšem vynikne až po zavedení obecně nestacionárního pole elektromagnetického, v němž dochází k proudění energie v prostoru a čase. Zůstáváme-li v rámci elektrostatiky, potom výrazy typu (1.60) , respektive (1.87) na jedné straně a výraz typu (1.90) na straně druhé představují pouze alternativní matematické vyjádření téže skutečnosti, tj. celkové energie potřebné k vytvoření daného elektrostatického pole.
V tomto článku shrneme obecné zásady pro výpočet intenzity elektrostatického pole (popř. jeho potenciálu), buzené známým rozložením elektrických nábojů. Obecný výklad doplníme několika typickými a z praktického hlediska užitečnými příklady.
1. Je-li zadána objemová hustota náboje r(r), plošná hustota náboje s(r) nebo lineární hustota náboje t(r), je vždy možné vypočítat intenzitu E(r) a potenciál j(r) elektrostatického pole v explicitní formě vzorců typu (1.69) a (1.70) . Přitom můžeme počítat E(r) i j(r) nezávisle na sobě nebo integrovat příslušný vzorec pro j(r) (což bývá v některých případech snazší) a pak určit intenzitu elektrostatického pole podle (1.50) . O volbě konkrétního postupu rozhodne obtížnost výpočtu jednotlivých integrálů. Přitom může nastat situace, že integrál pro j(r) diverguje, zatímco integrál pro E(r) konverguje.
2. Pokud je prostorové rozložení nábojů symetrické, je nejvýhodnější použít Gaussův zákon v integrálním tvaru (1.73) . Stačí najít uzavřenou plochu procházející daným bodem a obklopující zadané náboje tak, aby vektor intenzity elektrostatického pole měl na této ploše konstantní velikost a vhodný směr. Bude-li například k této ploše kolmý, platí
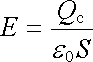 . . |
(1.92) |
Směr vektoru E je ovšem třeba určit z úvahy o symetrii soustavy.
3. Jde-li o geometricky nepravidelné nebo komplikované rozložení nábojů, mohou se předchozí způsoby ukázat nepoužitelné nebo příliš pracné. Jak bude ukázáno v článku 1.3.1, lze pak na vzdálenostech mnohem větších, než je rozměr oblasti s nenulovou hustotou náboje, určovat průběh elektrostatického pole a potenciálu přibližně pomocí tzv. multipólového rozvoje. Přitom je obvykle možné vystačit s dipólovým, nejvýše kvadrupólovým členem.
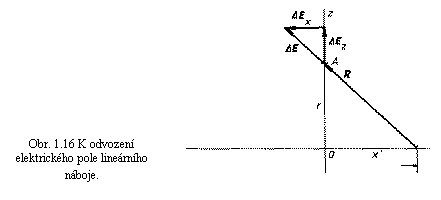
Nechť je na přímce, kterou ztotožníme s osou x, rovnoměrně rozložen náboj s lineární hustotou t (viz obr. 1.16). Vyšetříme elektrostatické pole v
obecném bodě A ve vzdálenosti r od přímky. Bez újmy na obecnosti
můžeme bodem A vést osu z; bod
A má pak souřadnice (0, 0, r). Intenzitu pole můžeme vypočítat
integrací podle vztahu
(1.69c)
. Vektor R směřující od vybraného elementu přímky Dxc
do bodu A má přitom složky (-xc,0,
r). Složka Ey = 0 a pro Ex a Ez dostáváme
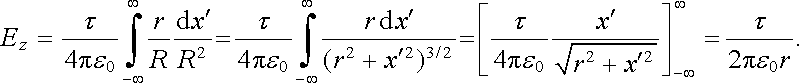 |
(1.93b) |
Od nuly je tedy různá jen složka z intenzity, jak bylo možné ihned usoudit ze symetrie soustavy.
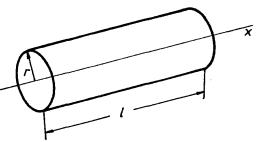
Výrazy (1.93) pro intenzitu pole lze získat podstatně jednodušeji pomocí Gaussova zákona. Zvolíme-li totiž Gaussovu plochu ve tvaru válcové plochy souosé s nabitou přímkou (obr. 1.17) a uvážíme-li, že z důvodů symetrie může být od nuly různá pouze složka intenzity kolmá k této přímce, dostaneme z Gaussova zákona
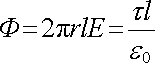 , , |
odkud okamžitě plyne výsledek (1.93) . Gaussův zákon můžeme ovšem použít pouze pro nekonečnou přímku, kdy nám symetrie zaručuje, že vektor intenzity bude k přímce kolmý a jeho velikost bude pouze funkcí vzdálenosti od přímky. V případě nabité úsečky bychom museli použít přímého integrování v příslušných mezích a složka Ex by již nebyla obecně nulová.
Rozložení potenciálu lze vypočítat podle vztahů (1.50) a (1.53) jako
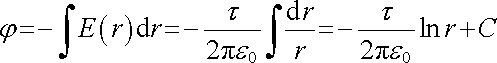 . . |
(1.94) |
Všimněte si, že konstantu C nemůžeme určit z podmínky, aby potenciál byl roven nule při r (R) yen. Je to opět způsobeno abstrakcí, kdy předpokládáme, že přímka je nekonečná a náboje jsou tudíž rozloženy i v nekonečnu.
Vyšetřme elektrostatické pole rovnoměrně nabité nekonečné
rovinné plochy s plošnou hustotou
náboje s (viz obr. 1.18). Pro řešení tohoto problému
bychom opět mohli použít vztahů
(1.69b)
, popř.
(1.70b)
. Počítání plošných
integrálů se však můžeme vyhnout, použijeme-li výsledku předchozího příkladu.
Můžeme si totiž představit uvažovanou plochu rozdělenou na úzké proužky,
jejichž lineární hustota náboje t = sDyc
a každý z nich přispívá v bodě A
intenzitou danou vztahy
(1.93)
. Celkovou intenzitu pak získáme integrací
příspěvků těchto proužků přes jedinou souřadnici yc.
Z důvodu symetrie stačí uvažovat pouze složky E kolmé k rovině,
které označíme
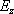 ;
vodorovné příspěvky symetricky položených proužků se vzájemně vyruší. Platí
;
vodorovné příspěvky symetricky položených proužků se vzájemně vyruší. Platí
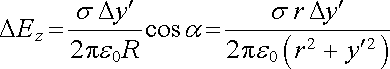 . . |
(1.95) |


Celkovou intenzitu pak vyjádříme integrálem
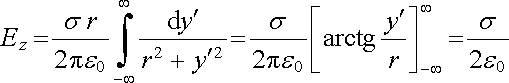 . . |
(1.96) |
K výsledku (1.96) dojdeme opět použitím Gaussova zákona. Uvážíme-li, že vzhledem k symetrii soustavy musí být vektor intenzity kolmý k nabité rovině, můžeme s výhodou zvolit Gaussovu plochu ve tvaru válce, jehož osa je k ní také kolmá. Celkový tok povrchem válce bude pak zřejmě dán pouze tokem jeho podstavami DS. Z Gaussova zákona dostáváme tedy podmínku
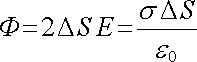 , , |
ze které ihned plyne vztah (1.96) .
Průběh potenciálu dostaneme integrací (1.96) podle r. Platí proto
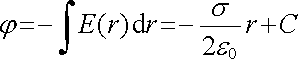 . . |
(1.97) |
Je zajímavé si všimnout, že výsledky (1.96) a (1.97) mají skutečně vlastnosti, které jsme pro pole plošně rozložených nábojů formulovali v předešlém výkladu. Zatímco potenciál je při průchodu nabitou plochou spojitý (nemá zde však derivaci), má intenzita pole nespojitost s /e0. Průběh intenzity pole a potenciálu kladně a záporně nabité roviny jsou znázorněny na obr. 1.19, kde E má hodnotu s /2e0.
Z výsledků vidíme, že zatímco pole bodového náboje klesá se vzdáleností jako 1/r2, klesá pole přímkového náboje pomaleji podle zákona 1/r a pole nabité roviny je homogenní a na vzdálenosti od roviny nezávisí. To se může zdát překvapivé, je to však důsledkem předpokladu, že nabitá rovina je nekonečná. Může být užitečné porovnat získané výrazy pro pole a potenciály bodového náboje, nabité přímky a roviny:
bod:
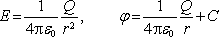 ,
,
přímka:
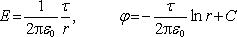 ,
,
rovina:
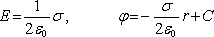 (1.98)
(1.98)
(r je vzdálenost daného bodu od bodového náboje, přímky, roviny).
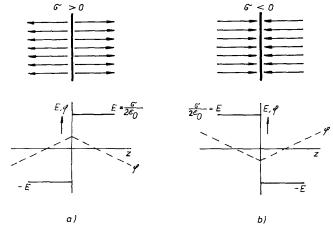
Obr. 1.19 Průběh elektrostatického pole roviny nabité: a) kladným nábojem, b) záporným nábojem.
Pomocí principu superpozice můžeme snadno určit průběh pole a potenciálu dvojice rovnoběžných nabitých rovin. Vzdálenost mezi nimi označíme d. Předpokládejme, že obě roviny jsou rovnoměrně nabity a že mají plošnou hustotu náboje téže velikosti, a to v jednom případě souhlasného, ve druhém nesouhlasného znamení. Pole obou rovin se superponují, takže vznikne situace znázorněná na obr. 1.20a, b.
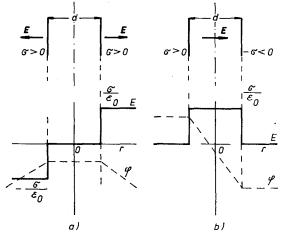
Obr. 1.20 Superpozice elektrostatických polí rovin nabitých: a) souhlasně, b) nesouhlasně.
Zvláště zajímavý je druhý případ nesouhlasně nabitých rovin, kdy homogenní elektrostatické pole velikosti
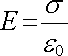 |
(1.99) |
je soustředěno v prostoru mezi oběma rovinami a mimo tuto oblast je pole nulové. S takovým uspořádáním se setkáváme u deskového kondenzátoru, viz článek 1.4.5. Superponujeme-li potenciál, zjistíme, že napětí mezi deskami je rovno
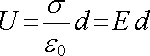 |
(1.100) |
a průběh potenciálu v prostoru mezi deskami je lineární
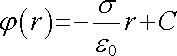 . . |
(1.101) |
Jak víme, je představa nekonečně tenké nabité plochy fyzikální idealizací. Ve skutečnosti reálná nabitá plocha, např. rovinná, má konečnou tloušťku a může být popsána pomocí objemové hustoty náboje r . Uvažme proto rovinnou vrstvu tloušťky a rovnoměrně nabitou s objemovou hustotou náboje r (obr. 1.21). Určíme intenzitu pole a potenciál v závislosti na vzdálenosti od osové roviny. Při výpočtu pole vně vrstvy budeme sčítat příspěvky tenkých rovinných vrstev, které budeme považovat za plošně nabité s hustotou Ds = rDr. Pak dostaneme
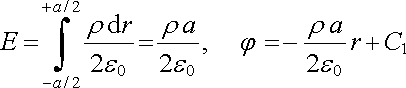 . . |
(1.102) |

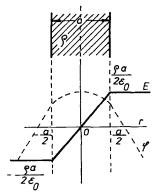
Vidíme, že při průchodu vrstvou se intenzita pole změní z -ra /2e0 na +ra /2e0, kde s = ra. Na hranici vrstvy musí být intenzita pole spojitá (nemusí zde však mít derivaci!) a potenciál musí být spojitý a musí mít derivaci. Skutečně, v libovolném vnitřním bodě vrstvy můžeme spočítat pole a potenciál jako superpozici pole dvou rovinných vrstev tloušťek (a /2) + r, (a /2) - r s tímto výsledkem:
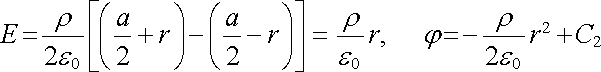 . . |
(1.103) |
Snadno ověříme, že za podmínky C1 - C2 = ra2 /8e0 řešení (1.102) a (1.103) mají při r = a/2 požadované vlastnosti. Průběh intenzity pole a potenciálu jsou znázorněny na obrázku 1.21.
Uvažujme kulovou plochu K o poloměru r0 rovnoměrně nabitou s plošnou hustotou náboje s ; celkový náboj slupky označíme Q. Vyšetříme elektrostatické pole vně i uvnitř této plochy. Integrování podle vztahů (1.69b) , (1.70b) je v tom-to případě obtížné, avšak sférická symetrie úlohy nám umožňuje použít Gaussův zákon. Jako Gaussovu plochu zvolíme nejprve soustřednou kulovou plochu o poloměru r > r0. Vzhledem k symetrii soustavy je nutné předpokládat, že vektor intenzity má v každém bodě Gaussovy plochy stejnou velikost a radiální směr, takže je k této ploše vždy kolmý. Podle Gaussova zákona dostaneme pro hledanou intenzitu
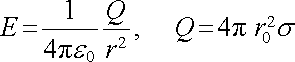 . . |
(1.104) |
Bude-li poloměr Gaussovy plochy r < r0, nebude v ní uzavřen žádný náboj, z čehož nutně vyplývá, že intenzita pole uvnitř plochy K je nulová.
Výraz pro průběh potenciálu vně koule dostaneme integrací vztahu (1.104) ; pro r (R) yen klademe j (R) 0, odkud vyplývá integrační konstanta C = 0, takže dostáváme
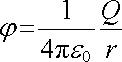 . . |
(1.105) |
Uvnitř koule bude potenciál zřejmě konstantní. S ohledem na jeho fyzikální smysl je třeba požadovat spojitý průběh při průchodu plochou K. Celkový průběh intenzity pole a potenciálu v závislosti na vzdálenosti od středu je znázorněn na obr. 1.22.
Všimněme si, že nespojitost intenzity při průchodu nabitou plochou má hodnotu s /e0 (jde o normálovou složku!). Z výrazů (1.104) a (1.105) je vidět, že vně koule K má elektrostatické pole stejný průběh jako pole bodového náboje Q umístěného v jejím středu, a to bez ohledu na vzdálenost od kulové plochy!
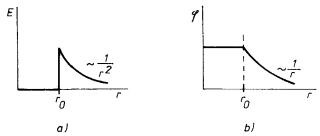
Obr. 1.22 Elektrostatické pole nabité kulové slupky: a) průběh intenzity, b) průběh potenciálu.
Nyní budeme uvažovat kouli poloměru r0 nesoucí náboj Q rovnoměrně rozložený po celém jejím objemu. Pro vyšetřování elektrostatického pole lze opět s výhodou použít Gaussův zákon. Pro body vně koule je možné přesně reprodukovat postup použitý v případě kulové slupky. Intenzita a potenciál budou tedy dány vztahy (1.104) a (1.105) s tím, že náboj Q označuje nyní celkový náboj koule objemově nabité s hustotou náboje r :
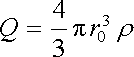 . . |
(1.106) |
Pro vyšetření intenzity uvnitř koule zvolíme, podobně jako v předchozím případu, soustřednou Gaussovu plochu o poloměru r < r0. Náboj Qc v ní uzavřený má velikost (4/3)pr3r. Podle Gaussova zákona tedy platí
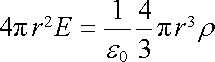 , , |
odkud
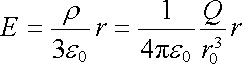 . . |
(1.107) |
Potenciál uvnitř koule dostaneme integrací vztahu (1.107) ve tvaru
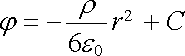 . . |
(1.108) |
Z požadavku spojitosti potenciálu pro r = r0 určíme hodnotu konstanty C a jako výsledek obdržíme
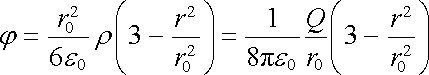 . . |
(1.109) |
Snadno se přesvědčíme, že potenciál má v bodě r = r0 spojité i derivace. Celkový průběh intenzity a potenciálu nabité koule v závislosti na vzdálenosti od středu je znázorněn na obr. 1.23.
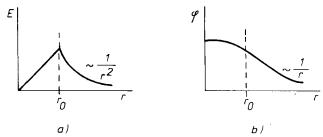
Obr. 1.23 Elektrostatické pole homogenně nabité koule: a) průběh intenzity, b) průběh potenciálu.
Obecně můžeme zřejmě usoudit, že jakékoliv sféricky symetrické uspořádání náboje (např. v koncentrických kulových vrstvách) v konečné oblasti prostoru se bude navenek chovat tak, jako by všechen náboj byl soustředěn ve středu této symetrie. Tato okolnost umožňuje nahradit pole nabitých koulí bodovými náboji umístěnými v jejich středu, podobně jako v případu gravitačního pole můžeme považovat sféricky symetrická nebeská tělesa za hmotné body. Naopak odchylka od pole bodového náboje (v případu gravitace od pole hmotného bodu) svědčí o narušení sférické symetrie, což má velký praktický význam. K tomuto poznatku dospěl již I. Newton pracným integrováním, nemaje po ruce Gaussův zákon.
Při výpočtu intenzity pole a potenciálu plošně nebo objemově nabitého nekonečného válce můžeme opět využít Gaussův zákon a postupovat obdobně jako u náboje s kulovou symetrií. Vektor intenzity pole bude zřejmě kolmý k válcové ploše a Gaussovu plochu můžeme volit jako koaxiální válcovou plochu libovolné délky l, procházející daným bodem ve vzdálenosti r od osy válce. Je-li poloměr válcové plochy r0 , můžeme zkoumat pole uvnitř válce (r lb r0) a vně válce (r > r0). Lze očekávat, že v případu cylindricky symetrického rozdělení náboje bude pole vně válce ekvivalentní poli nabité přímky totožné s osou válce. Pro úplnost uvedeme získané výsledky; tak dostáváme pro válec povrchově nabitý s hustotou náboje s
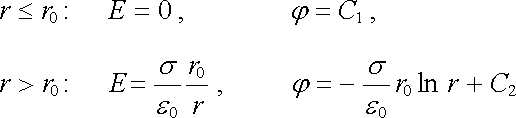 |
(1.110) |
a pro válec objemově nabitý s hustotou náboje r
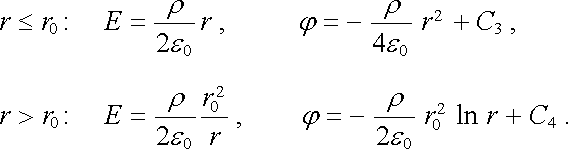 |
(1.111) |
Integrační konstanty nemůžeme tentokrát určit z podmínky j (R) 0 při r (R) yen podobně jako u nabité koule. Je to důsledek přijaté idealizace nekonečného válce s náboji v nekonečnu. Tato okolnost však není na závadu, neboť volba konstanty ve výrazu pro potenciál neovlivní fyzikální výsledek.
Určeme intenzitu elektrostatického pole a potenciál na ose kružnice poloměru R, na níž je rovnoměrně rozložen náboj lineární hustoty t. Budeme sčítat příspěvky k vektoru intenzity pole vždy od dvojice protilehlých malých lineárních nábojů tDl na kružnici (viz obr. 1.24a). Vektor intenzity bude zřejmě ležet v ose kružnice a pro jeho velikost v bodě o výšce h nad rovinou kružnice dostaneme
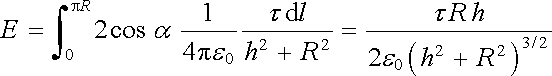 . . |
(1.112) |
Integrací získáme potenciál
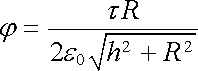 . . |
(1.113) |
Průběh veličin E a j v závislosti na výšce
h je znázorněn na obr. 1.24b. Všimněme si změny orientace pole při
průchodu rovinou kružnice a extrémů ve vzdálenostech hm = R/
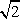 .
.
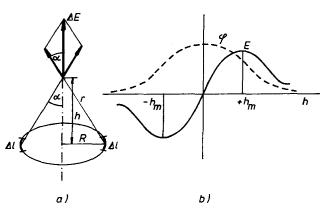
Obr. 1.24 a) K odvození
elektrostatického pole na ose nabité kruhové smyčky,
b) průběh intenzity elektrostatického pole a potenciálu na ose nabité kruhové
smyčky.
Výsledek získaný v předchozím příkladu můžeme uplatnit například při výpočtu pole na ose válce konečné délky. Mějme válcovou plochu délky L a poloměru R plošně nabitou s hustotou náboje s (obr. 1.25). Označme vzdálenost bodu na ose této plochy od středu válce jako h. Válcovou plochu můžeme rozřezat na koaxiální pásy výšky Dl a považovat je za nabité kružnice o lineární hustotě náboje sDl. Použitím vztahu (1.113) a jeho integrací pak dostaneme
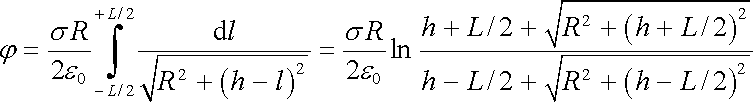 . . |
(1.114) |
R
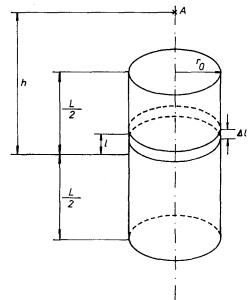
Intenzitu pole určíme snadno jako E(h) = -dj/dh a ověříme, že ve středu válce je pole nulové a potenciál maximální.

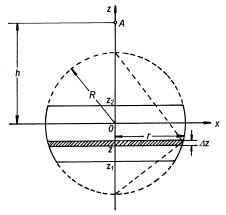
Mějme kulovou plochu poloměru R nabitou s plošnou hustotou náboje s. Vyřízneme z ní kulový pás vymezený souřadnicemi z1, z2 (obr. 1.26). Určíme potenciál na ose pásu ve výšce h měřené od středu kulové plochy. Uvažovaný kulový pás rozřežeme na použky velmi malé výšky Dz o souřadnici z a poloměru R. Vezmeme v úvahu, že obsah plochy takového kulového proužku je roven DS = 2pRDz. Opět použijeme výraz pro potenciál na ose nabité kružnice (1.113) , kam dosadíme za lineární hustotu t
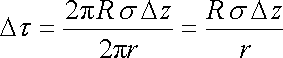 . . |
Dále použijeme Euklidovu větu, podle níž r2 = (R + z)(R - z). Hledaný potenciál se pak rovná vztahu
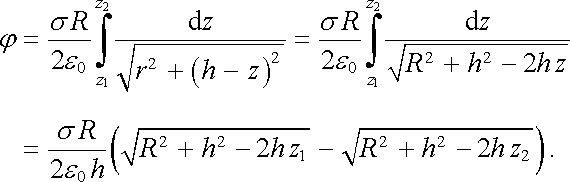 |
(1.115) |
Intenzitu pole stanovíme opět jako E(h) = -dj/dh.
Jako zvláštní případ můžeme určit například potenciál vytvářený polokulovou slupkou (z1 = -R, z2 = 0) ve středu kulové plochy (h = 0) a ve vrcholu kulové plochy (h = R). Po pečlivém limitování (1.115) a výrazu pro intenzitu pole dostaneme
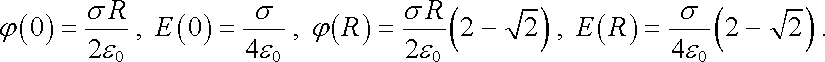 |
(1.116)
Bude-li kulová plocha uzavřena (z1 = -R, z2 = R), dostaneme uvnitř koule nulové pole a konstantní potenciál j = s R/e0, vně koule potenciál klesající s h jako j = s R2/e0 h a intenzitu pole E = s R2/e0 h2 .
Určíme elektrostatickou interakční energii spojitého uspořádání náboje, jaké představují plošně nabitá kulová slupka a objemově nabitá koule poloměru R. V případě plošně nabité kulové slupky využijeme znalosti potenciálu na jejím povrchu, který je roven
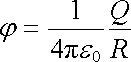 , , |
a dále vztahu (1.87) upraveného na plošné integrování. Potom
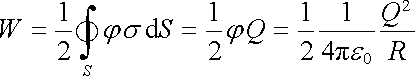 . . |
(1.117) |
V případě objemově nabité koule si připomeneme definici, podle níž je energie soustavy nábojů dána prací potřebnou k vytvoření této soustavy, přičemž nezáleží na pořadí sbližování nábojů. Můžeme proto například předpokládat, že objemově nabitá koule vznikla tak, že postupně přibírala koncentrické vrstvy náboje, podobně jako se vytváří velká sněhová koule. Dosáhne-li koule poloměru r a náboje q a přibere další vrstvu náboje tloušťky dr, zvýší se její energie o
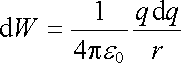 . . |
(1.118) |
S kulovým nábojem q = (4/3)pr3r a přírůstkem náboje dq = 4pr2rdr zacházíme jako se dvěma bodovými náboji. Integrací výrazu (1.118) v mezích 0 ¸ R dostaneme
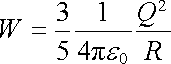 . . |
(1.119) |
Kdybychom považovali elementární nabitou částici (například elektron) za kulový náboj a přirovnali její celkovou energii danou relativistickým vztahem (2.18) W = mc2 (m je hmotnost částice, c rychlost světla ve vakuu) k energii elektrostatické (1.119) , mohli bychom odhadnout rozměry této částice. Při tomto řádovém odhadu se koeficient 3/5 zpravidla neuvažuje; potom dostáváme tak zvaný klasický poloměr elektronu rovný
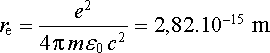 . . |
(1.120) |
Je ovšem třeba podotknout, že zřejmě nejde o skutečný poloměr elektronu, nýbrž pouze o kombinaci základních konstant, která má rozměr délky a může hrát určitou roli ve fyzice elementárních částic. Podle výsledků dosud provedených experimentů se elektron chová jako bodová částice i při rozměrech značně menších, než je tento "klasický poloměr". Na druhé straně je zřejmé, že kdyby se rozměry částice zmenšovaly k nule, její elektrostatická energie by musela narůstat do nekonečna.