Na základě pokusů s elektřinou víme, že některá tělesa (například skleněná či ebonitová tyč po předchozím tření) mohou za určitých podmínek silově působit na jiná tělesa. Toto silové působení si vysvětlujeme přítomností elektrických nábojů. Elektrický náboj představuje pro nás výchozí fyzikální veličinu, přičemž mírou jejího množství a rozložení na příslušných tělesech je právě silové působení mezi nimi. Elektrický náboj je veličinou skalární, podobně jako hmotnost, a k jeho určení postačí jediná (reálná) číselná hodnota. Skutečnost, že síly elektrického působení mezi tělesy mohou být jak přitažlivé, tak odpudivé, vysvětlujeme tím, že elektrický náboj může nabývat kladných i záporných hodnot - tělesa se souhlasným znamením náboje se přitom odpuzují, tělesa s nesouhlasným znamením náboje se přitahují. Tělesa, která nesou elektrický náboj, nazýváme kladně či záporně nabitá, tělesa o nulovém náboji jsou elektricky neutrální, nenabitá. Často se setkáváme s případem, kdy na tělesech jsou odděleně rozloženy kladné a záporné elektrické náboje o téže absolutní hodnotě. Taková tělesa budou také elektricky silově působit, přestože jejich celkový elektrický náboj je nulový. Říkáme jim polarizovaná.
O přítomnosti elektrického náboje se přesvědčujeme pouze na základě jeho silového působení. Znamená to, že existenci jednoho jediného náboje bychom nemohli nijak odhalit. Kdyby existovaly pouze dva náboje, mohli bychom určit, zda jsou souhlasného či nesouhlasného znamení; nemohli bychom však rozhodnout ani o znamení, ani o velikosti těchto nábojů. Teprve jsou-li k dispozici alespoň tři náboje, můžeme jeden z nich vybrat jako jednotkový a kladný a ze silového působení určit velikost a znamení druhých dvou nábojů.
Co je vlastní podstatou elektrického náboje nevíme. Na základě poznatků současné mikrofyziky jej můžeme považovat za jednu z vlastností některých elementárních částic, která podmiňuje jejich vzájemné působení. Rozlišujeme čtyři základní typy vzájemného působení (interakce) mezi elementárními částicemi: gravitační, slabé, elektromagnetické a silné. Gravitační interakce je univerzální a týká se všech částic. Setkali jsme se s ní v mechanice, její velikost udává Newtonův gravitační zákon a její podstatu se snaží objasnit obecná teorie relativity. Slabá interakce se projevuje u některých typů radioaktivního rozpadu za účasti neutrina. Podobně elektromagnetická interakce se uplatňuje mezi elementárními částicemi a jednou z jejích charakteristik je elektrický náboj. Silná interakce existuje mezi částicemi, které nazýváme hadrony, a drží pohromadě atomové jádro, které by se jinak odpudivými elektrickými silami působícími mezi protony muselo rozletět.
Současný rozvoj mikrofyziky naznačuje, že hadrony, které jsme dříve považovali za elementární, mají svoji strukturu a komponenty. Předpokládáme o nich, že jsou tvořeny tzv. kvarky. Na současné úrovni vystupují tedy jako elementární kvarky a leptony (k nim patří elektron, mion, tauon a odpovídající neutrina), jejich antičástice a dále pak částice, které zprostředkují interakci mezi nimi. U gravitační interakce jsou to dosud hypotetické gravitony, u slabé nedávno objevené intermediální bosony, u elektromagnetické fotony a u silné gluony [l].
Elementární částice vytvářejí složitější struktury, atomová jádra, atomy, molekuly, jejichž vzájemné působení nabývá rovněž složitého charakteru. V denním životě se setkáváme s projevy působení gravitačního a elektromagnetického, které je ze všech nejlépe prozkoumáno. Nejen síly elektrostatické a elektrodynamické, ale i magnetické, optické, chemické a biologické jevy, chemické vazby a uvolňování chemické energie, mezimolekulámí síly podmiňující soudržnost těles, přilnavost a tření, síly svalové kontrakce, tepelné působení slunečního záření a mnoho dalších jevů má svůj původ ve vzájemném působení elektrických nábojů.
Síly elektromagnetického působení mohou být přitažlivé i odpudivé, mohou složitým způsobem záviset na vzdálenosti, směru v prostoru a vzájemné poloze těles, na rychlosti jejich pohybu, vlastnostech prostředí, obecně nemusí působit ve směru spojnice interagujících těles, a dokonce nemusí ani splňovat Newtonův zákon akce a reakce.
Elektrický náboj má některé základní vlastnosti, které vyplývají z experimentálních pozorování a uplatňují se i při vzájemné interakci nabitých částic. Tyto vlastností vyjadřuje:
1. Zákon zachování náboje. Elektrický náboj je nestvořitelný a nezničitelný. Jinak řečeno, celkové množství elektrického náboje v elektricky izolované soustavě (jejíž hranicí nemohou procházet náboje) zůstává neměnné. Dochází-li ke srážkám částic, je celkový náboj před reakcí roven celkovému náboji po reakci. První experimentální důkaz tohoto zákona podal Faraday v r. 1843 elektrometrickým měřením náboje nabité koule v izolovaném prostoru. Matematické vyjádření tohoto zákona je dáno tzv. rovnicí kontinuity proudu, kterou uvedeme v článku 3.1.3.
2. Zákon invariantnosti náboje. Velikost elektrického náboje se při pohybu nemění. Jinak řečeno, při všech transformacích vztažné soustavy zůstává velikost náboje invariantní. Takovou vlastnost má jen málo fyzikálních veličin; například hmotnost částice roste jak známo s rychlostí.
Jedním z experimentálních argumentů svědčících o invariantnosti náboje je skutečnost, že atomy a molekuly jsou elektricky neutrální. Atom helia a molekula těžkého vodíku D2 jsou tvořeny týmiž částicemi - dvěma protony, dvěma neutrony a dvěma elektrony. Pohyb nabitých částic v těchto dvou soustavách je jistě podstatně odlišný a přitom obě zůstávají elektricky neutrální. V šedesátých letech 20. století byly prováděny přesné pokusy s odchylováním svazků atomů cesia a molekul vodíku v silném elektrickém poli, které prokázaly, že atomy jsou elektricky neutrální s přesností na dvacet desetinných míst velikosti elementárního náboje[1].
3. Zákon kvantování náboje. Existuje nejmenší, dále nedělitelný elektrický náboj, který nazýváme elementárním, a všechny elektrické náboje mají velikost, která je jeho celistvým násobkem. Tento atomismus elektřiny souvisí s tím, že elektrický náboj je vlastností částic látky. Velikost elementárního náboje je možné určit pomocí celé řady experimentů, např. klasického Millikanova pokusu (1911) , viz článek 1.1.3.
Kladný elementární náboj má například proton, který patří mezi hadrony. Kvarky jako komponenty hadronů mají podle předpokladů náboje o velikosti jedné třetiny a dvou třetin elementárního náboje. Tato okolnost však nemění nic na faktu kvantování náboje.
Pokud jde o vlastnosti nabitých částic, jsou pozoruhodné ještě dvě okolnosti. Jednou z nich je existence částic a antičástic. Ke každé částici existuje antičástice, které se vzájemně liší znamením elektrického náboje.[2] Protože elektrické síly závisejí pouze na souhlasnosti či nesouhlasnosti znamení náboje, mohla by existovat antilátka, kde by nukleony v atomových jádrech byly nahrazeny antinukleony a elektrony atomových obalů svými antičásticemi - pozitrony. Tyto úvahy mají velký význam i pro kosmologii a vyjadřují jednu ze základních symetrií přírody.
Druhá ze zmíněných okolností je nábojová kvazineutralita vesmíru. V dostatečně velkých objemech se celkový počet kladných i záporných nábojů vždy vyrovnává a látka, jak se s ní běžně setkáváme v tuhém, kapalném a plynném skupenství, se jeví elektricky neutrální. Odchylky od elektrické neutrality v makroskopických měřítcích se projevují elektrickými silami, které se opět snaží elektrickou neutralitu obnovit.
Při kvantitativním popisu silového působení mezi makroskopickými nabitými tělesy je výhodné v prvním přiblížení abstrahovat od způsobu rozložení náboje v objemu tělesa. Můžeme zavést pojem bodového náboje, který je analogický pojmu hmotného bodu v mechanice. Za bodový náboj můžeme tedy považovat nabité těleso, jehož rozměry jsou zanedbatelně malé ve srovnání se vzdálenostmi, na nichž silové působení uvažujeme.
Dvojice bodových nábojů o velikostech, Q1 , Q2 , které jsou umístěny ve vakuu v bodech o polohových vektorech r1, r2 a které jsou nehybné v dané inerciální soustavě souřadnic (obr. 1.1), tvoří nejjednodušší makroskopickou soustavu, na níž je možné silové působení mezi náboji studovat. Experimenty tohoto druhu provedl r. 1785 Ch. A. Coulomb s použitím torzních vah, které představují jeden z nejcitlivějších fyzikálních přístrojů.
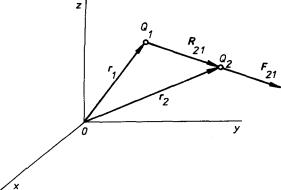
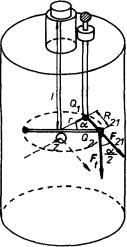
Sílu působící mezi dvěma malými nabitými kuličkami lze měřit z úhlu zkrutu dlouhého a tenkého vlákna délky l a poloměru průřezu R. Úhel se zjišťuje odrazem světelného paprsku od zrcátka Z spojeného s vláknem. Na konci vlákna je zavěšeno vodorovné vahadélko s malými stejnými kuličkami na koncích. Jedna z těchto pohyblivých kuliček nesoucí elektrický náboj Q2 se ustálí v rovnovážné poloze vůči nehybné kuličce o náboji Q1 ve vzdálenosti R21 (viz obr. 1.2). Jak uvidíme později, nabitá kulička se navenek chová tak, jakoby elektrický náboj byl umístěn v jejím středu a popsané uspořádání tedy umožňuje měřit síly působící mezi bodovými náboji. Moment tangenciální síly Ft se musí rovnat torznímu momentu D takže platí
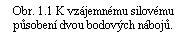

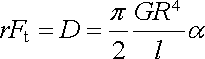 |
(1.1) |
(r je délka ramene torzních vah, G modul smyku materiálu vlákna), a tedy
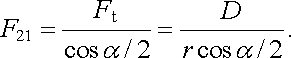 |
(1.2) |
Na základě výsledků těchto experimentů lze formulovat vztah vyjadřující sílu F21, kterou náboj Q1 působí na náboj Q2. Tento vztah, vyjadřující Coulombův zákon, lze napsat ve tvaru
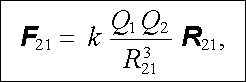 |
(1.3) |
v němž R21 = r2 - r1 a R21 je velikost vektoru R21. Obráceně sílu F12, kterou působí náboj Q2 na náboj Q1, dostaneme záměnou indexů l a 2 ve vztahu (1.3) . Platí tedy F21 = -F12 v souladu s Newtonovým principem akce a reakce. Síly mezi bodovými náboji působí podél jejich spojnice - takové síly nazýváme centrálními. Změní-li se znaménko součinu Q1Q2, změní se pouze směr síly a nikoli její velikost. Kladné znaménko tohoto součinu odpovídá přitom síle odpudivé, záporné znaménko síle přitažlivé.
Velikost síly působící mezi dvojicí bodových nábojů je rovna
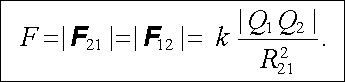 |
(1.4) |
Tato velikost klesá se čtvercem vzdálenosti obou nábojů (stejně jako gravitační působení dvou hmotných bodů) a nezávisí na směru v prostoru. Coulombovy síly jsou tedy izotropní.
Všimneme si nyní poněkud obecnější úlohy. Předpokládejme, že v bodech o polohových vektorech r1, r2,..., rN jsou rozloženy bodové náboje Q1, Q2, ..., QN. Nechť dále v bodě o polohovém vektoru r je umístěn bodový náboj Q. Ptáme se, jaká síla F bude na náboj Q působit. Abychom na tuto otázku mohli odpovědět, musíme vědět, jak se změní silové působení mezi dvojicí bodových nábojů, budou-li v prostoru rozmístěny ještě náboje další.
Experimentální zkušenost ukazuje, že silové působení mezi danou dvojicí nábojů je na přítomnosti dalších nábojů nezávislé. Podle věty o skládání sil, známé z mechaniky, můžeme proto celkovou sílu F působící na náboj Q vyjádřit jako vektorový součet sil Fi (i = 1, ..., N) vyvolaných jednotlivými náboji Q1 až QN. Podle (1.3) bude tedy platit
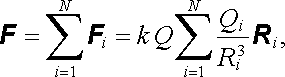 |
(1.5) |
přičemž Ri = r - ri.
Elektrostatické síly působící mezi dvojicemi bodových nábojů jsou tedy nezávisle aditivní. Toto tvrzení je obsahem principu superpozice, podle něhož se jednotlivé síly (popř. jiné fyzikální veličiny) vzájemně neovlivňují, superponují se a lze je sčítat. Jde o neobyčejně významný princip, s nímž se setkáváme i v jiných oblastech fyziky u tzv. lineárních jevů. Umožňuje nám určovat silové působení těles s libovolným rozložením elektrických nábojů. Je vlastně součástí formulace Coulombova zákona, neboť umožňuje použít vztah (1.3) i za přítomnosti nábojů dalších.
Přesnost Coulombových měření byla řádově několik procent. Existují však další, mnohem přesnější nepřímé metody experimentálního ověření platnosti Coulombova zákona, založené na vlastnostech rozložení elektrických nábojů na vodičích. Této metody využil již H. Cavendish r. 1772, své výsledky však nepublikoval a upozornil na ně teprve J. C. Maxwell r. 1879. Podrobněji bude o této metodě zmínka v článku 1.4.3.
V pozemském makroskopickém měřítku je platnost Coulombova zákona experimentálně potvrzena mimo pochybnost. Vzniká samozřejmě otázka o mezích platnosti tohoto zákona, budou-li elektrostatické síly a vzdálenosti nábojů příliš velké nebo příliš malé. Pokusy s rozptylem nabitých částic prokázaly platnost Coulombova zákona až na vzdálenostech odpovídajících rozměrům 10-17 m. Astrofyzikální poznatky, především skutečnost, že elektromagnetické vlnění neprojevuje disperzi při šíření ve vakuu a že foton má nulovou klidovou hmotnost, svědčí o tom, že platnost Coulombova zákona není omezena ani velkými vzdálenostmi dostupnými našemu pozorování.
Coulombův zákon spolu s principem superpozice má pro elektrostatiku charakter základního zákona a v jistém smyslu vyčerpává její obsah. Umožňuje určit silové působení libovolně rozložených elektrických nábojů a spolu se zákony mechaniky též podmínky rovnováhy nabitých těles. Centrální a izotropní charakter Coulombových sil je důsledkem obecného principu symetrie - nehybný bodový náboj v prostoru můžeme považovat za střed kulové symetrie, dvojice bodových nábojů udává jediný význačný směr daný jejich spojnicí. Vlastním fyzikálním obsahem Coulombova zákona je tedy především závislost poklesu velikosti síly na vzdálenosti podle zákona převráceného čtverce.
Stojí za zmínku, že Coulomb prováděl analogické experimenty též s dlouhými tenkými tyčovými magnety a nalezl tak analogický "Coulombův zákon pro magnetické náboje". Později se však ukázalo, že samostatné "magnetické náboje" neexistují. K této otázce se vrátíme v kapitole 3.
Coulombův zákon slouží zároveň jako definiční vztah nové fyzikální veličiny, elektrického náboje, i jeho míry. Z hlediska formální logiky by se mohlo zdát, že tak ztrácí charakter zákona. Nesmíme však zapomenout na to, že fyzika, na rozdíl od matematiky, pracuje se základními pojmy, které jsou vlastnostmi reálných objektů a jejichž existence není otázkou logiky, nýbrž experimentální zku-šenosti. Chápeme-li zavedení elektrického náboje tímto způsobem, můžeme dále rozvíjet fyzikální teorii pomocí matematického a logického formalismu.
Volbou konstanty úměrnosti k v Coulombově zákoně (1.3) nebo (1.4) stanovíme jednotku velikosti elektrického náboje. V dalším výkladu budeme mluvit pouze o elektrickém náboji a ze souvislosti bude zřejmé, zda jde o fyzikální vlastnost nebo její kvantitativní určení, velikost.
Fyzikální jednotky tvoří, jak známo, koherentní soustavy založené na několika jednotkách základních, z nichž jsou ostatní odvozovány. Dnes je u nás uzákoněna Mezinárodní soustava jednotek SI, která se stále více uplatňuje ve vědě i v praxi (viz Dodatek 2). Mezi základními jednotkami této soustavy je jednotka elektrického proudu ampér. Jednotkou elektrického náboje je pak ampérsekunda zvaná též coulomb (C). Abychom zachovali soulad se základními jednotkami Mezinárodní soustavy, musíme v Coulombově zákonu položit
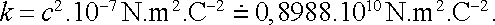 |
(1.6) |
Zdůvodnění této volby podáváme v článku 3.3.2, kde uvidíme, jak souvisí s volbou základních jednotek Mezinárodní soustavy. Všimněme si, že námi zvolená konstanta k je vyjádřena prostřednictvím univerzální konstanty c (rychlost světla ve vakuu). Konstanta k se obyčejně zapisuje ve tvaru
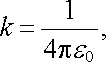 |
(1.7) |
kde (srov. Dodatek 2)
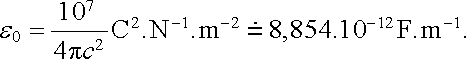 |
(1.8) |
Nově zavedená konstanta e0 (epsilon nula) má tedy rovněž charakter univerzální fyzikální konstanty a nazývá se permitivita vakua. Její fyzikální význam bude objasněn později. Rovněž jednotka farad F = C2. N-1. m-1 bude zavedena později jako jednotka kapacity.
Nyní se můžeme zeptat, jakou velikost má elementární náboj. Přímou metodou byla změřena R. A. Millikanem r. 1911; Millikanův experiment je zároveň i důkazem atomismu elektřiny (kvantování náboje).
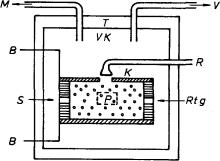
Velikost elementárního náboje e lze určit porovnáním sil, kterými působí elektrostatické a gravitační pole na malá nabitá tělíska. Mezi desky kondenzátoru jsou vstřikovány olejové kapičky a mikroskopem je sledován jejich vertikální pohyb v přítomnosti elektrického pole a bez něho. Uspořádání experimentu je patrné z obr. 1.3.
Označme r poloměr kapky, q náboj kapky, s hustotu oleje, r hustotu vzduchu při daném tlaku, h dynamickou viskozitu vzduchu, vg, vE vertikální rychlosti kapek při vypnutém a zapnutém napětí na kondenzátoru. Síla tření při pohybu kulových kapiček ve zředěném plynu je dána Stokesovým vzorcem FS = 6phrv a roste se stoupající rychlostí tak dlouho, až se pohyb kapky stane rovnoměrným. Potom máme pro celkovou sílu působící na kapku při vypnutém kon-denzátoru
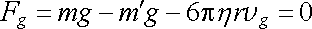 , , |
(1.9) |
kde
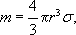
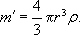
Při zapnutém kondenzátoru působí na tutéž kapku síla
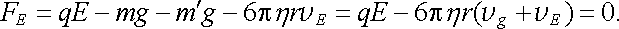 |
(1.10) |

Z těchto dvou rovnic určíme poloměr kapky (obtížně měřitelný) a velikost náboje
(eq0013)SETEQ(eq0014) (1.11)
Proměřováním rychlosti pohybu mnoha kapek zjistíme, že jejich náboje jsou malými násobky určitého minimálního, elementárního náboje, který tak můžeme určit.
Jsou-li rozměry kapek srovnatelné s délkou volné dráhy molekul l, je třeba Stokesovu sílu FS dělit výrazem l + A(l/r) = l + (B/pr), kde p je tlak plynu a A, B neznámé konstanty. Znalost těchto konstant není však nutná. Určujeme-li elementární náboj pro různé hodnoty tlaku p a vynášíme-li lineární závislosti mezi q2/3a 1/pr, můžeme opravenou hodnotu určit extrapolací.
Millikanův experiment byl mnohokrát opakován; A. F. Ioffe změřil r. 1912 obdobným způsobem náboj elektronů uvolňovaných při fotoelektrickém jevu.
Přesněji lze určovat měrný náboj částic q/m (q je náboj, m klidová hmotnost částice). Lze k tomu použít například vlastností pohybu nabitých částic v ele-ktrických a magnetických polích (viz kapitola 6).
Známe-li velikost náboje, který při elektrolýze vyloučí jeden mol jednovazných iontů nesoucích po jednom elementárním náboji (tj. Faradayův náboj F - viz článek 7.4.2), a počet těchto iontů v jednom molu (tj. Avogadrovu konstantu N0), najdeme velikost elementárního náboje e jako poměr dvou konstant:
(eq0015)SETEQ(eq0016)
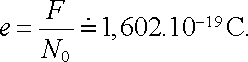 |
(1.12) |
Poznamenejme, že klidová hmotnost elektronu je me B 9,109.10-31 kg, a jeho měrný náboj tedy -e/me B -1,759.1011 C.kg-1. (Podrobněji o metodách určování elementárního náboje viz [2].)
Při zkoumání elektrických sil nemáme zpravidla co činit s jednotlivými bodovými či elementárními náboji, ale s nabitými makroskopickými tělesy. Jde tedy o velké soubory nabitých částic, které jsou rozloženy v objemu, popř. na povrchu tělesa, s velkou hustotou tak, že toto rozložení můžeme považovat za spojité. Nejde zde ovšem o spojitost v matematickém smyslu, nýbrž ve smyslu fyzikálním: zvolíme-li "nekonečně malý" (diferenciální) objem nabitého tělesa, budeme stále předpokládat, že obsahuje velké množství elementárních nábojů, takže se neprojeví kvantování náboje.
Podobně, jako jsme zaváděli pojem hustoty v souvislosti s rozložením hmotnosti v mechanice, můžeme zavést pojem objemové hustoty náboje r. Uvažujme těleso libovolného tvaru o objemu V, které je v klidu vůči dané inerciální soustavě. Předpokládejme, že toto těleso nese náboj Q, jehož rozložení po celém objemu tělesa je časově neproměnné. Okamžitě můžeme definovat střední objemovou hustotu náboje jako poměr
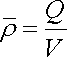 . . |
(1.13) |
Zvolme nyní v objemu tělesa bod A polohy r o (x, y, z) a obklopme tento bod objemem DV. Objem DV nese náboj DQ. Objem DV budeme libovolným způsobem zmenšovat tak, aby stále obsahoval bod A, a budeme předpokládat, že existuje limita nezávislá na způsobu zmenšování objemu DV
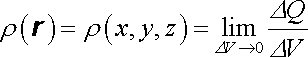 . . |
(1.14) |
Funkci r(r) nazveme objemovou hustotou náboje v daném bodě. Náboj tělesa objemu V charakterizovaného objemovou hustotou náboje r najdeme jako
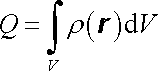 . . |
(1.15) |
Naopak vztah (1.15) můžeme též považovat za definici objemové hustoty náboje r. Náboj malého objemu DV můžeme přibližně vyjádřit vztahem
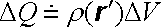 , , |
(1.16) |
kde r c je polohový vektor libovolného bodu objemu DV; pro nekonečně malý (diferenciální) objem bude vztah (1.16) platit přesně. Ve zvláštním případě rovnoměrného rozložení náboje je r konstanta a integrál (1.15) se redukuje na vztah[3]
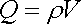 . . |
(1.17) |
Kromě uvažovaného rozložení náboje v objemu je myslitelné uvažovat rozložení náboje na geometrických útvarech jiného typu. Pro náboje rozložené na dané ploše S dospějeme obdobným limitním přechodem k pojmu plošné hustoty náboje s(r). Náboj na ploše S charakterizované plošnou hustotou náboje s je pak
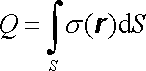 , , |
(1.18) |
ve zvláštním případě rovnoměrného rozdělení náboje
(eq0024). (1.19)
Podobně je možné uvažovat rozložení náboje na křivce. V tomto případě zavedeme pojem lineární hustoty náboje. Náboj na křivce délky l charakterizované lineární hustotou náboje t je
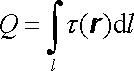 , , |
(1.20) |
v případě rovnoměrného rozložení náboje
Q = t l. (1.21)
Názorný význam všech zavedených hustot náboje je zřejmý. Každá z nich vyjadřuje velikost náboje, který v okolí daného bodu připadá na jednotkovou míru daného útvaru. Pro jednotky těchto veličin v Mezinárodní soustavě máme (r) = C.m-3, (s) = C.m-2, (t) = C.m-1. Jde tedy o fyzikálně různé veličiny, které jak uvidíme mají též různé vlastnosti, zejména v oblastech přechodu od nulových k nenulovým hustotám. Je ovšem třeba vidět, že ve skutečnosti rozložení nábojů nemůže být nikdy dvojrozměrné či jednorozměrné v matematickém smyslu. Pro účely makroskopického popisu je však výhodné mikrofyzikální strukturu rozložení nábojů pominout.
Vraťme se k obecné soustavě bodových nehybných nábojů Q1 až QN rozmístěných ve vakuu v bodech r1 až rN. Tyto náboje na sebe působí Coulombovými elektrostatickými silami a mají-li zůstat nehybné, musí být na svých místech nějakým způsobem udržovány. Dále je zřejmé, že při vytváření takové soustavy musí vnější síly překonávat síly Coulombovy, a musí tedy konat práci. Práce vnějších sil (která je rovna záporně vzaté práci vykonané Coulombovými silami) odpovídá elektrostatické potenciální energii soustavy nábojů. Nezbytným předpokladem ovšem je, aby tato energie nebyla závislá na způsobu vytváření soustavy, tj. na pořadí a způsobu pohybu nábojů z počátečních do konečných poloh. Potenciální energie pak může být považována za charakteristiku této soustavy. Přesvědčíme se nyní o této důležité vlastnosti.
Začneme s jedním izolovaným bodovým nábojem Q1. Je-li druhý bodový náboj Q2 nekonečně vzdálen, bude síla mezi nimi působící nekonečně malá a potenciální energii takové dvojice nábojů můžeme položit rovnu nule. Budeme nyní přibližovat náboj Q2 nejkratší cestou po přímce směřující k náboji Q1 , až se náboj Q2 zastaví v bodě A ve vzdálenosti R12 od náboje Q1. Přitom jsme vykonali práci při překonávání Coulombovy síly (1.1) rovnou
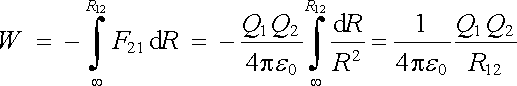 . . |
(1.22) |
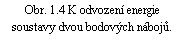
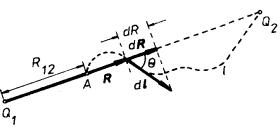
Budeme-li náboj Q2 přibližovat po libovolné dráze l (obr. 1.4), dostaneme
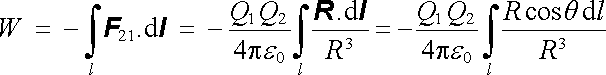 |
(1.23) |
s týmž výsledkem jako v předchozím případě, neboť dR = cosq dl.
Výsledná práce tedy nezávisí na způsobu sbližování nábojů. Přiblíží-li se k této dvojici třetí náboj Q3, bude podle principu superpozice výsledná potenciální energie rovna
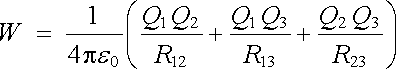 . . |
(1.24) |
Obecně pro soustavu N bodových nábojů můžeme napsat
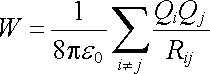 . . |
(1.25) |
Sčítáme přes všechna vzájemně různá i a j, takže se každá dvojice nábojů uvažuje dvakrát, a proto je třeba doplnit navíc činitel 1/2. Samozřejmě platí Rij = Rji = |rj - ri |. Získaná potenciální energie charakterizuje výsledný stav soustavy bodových nábojů a může být kladná, záporná i nulová.
Snadno se přesvědčíme, že existují taková uspořádání kladných a záporných elektrických nábojů v prostoru, kdy na každý z nábojů působí nulová výslednice Coulombových sil. Mějme například kladný bodový náboj Q0 umístěn v počátku kartézské soustavy souřadnic a dva záporné bodové stejně velké náboje Q na ose x v bodech o souřadnicích x = a a x = -a (obr. 1.5). Na centrálně umístěný náboj Q0 působí ze strany druhých dvou nábojů zřejmě nulová výslednice sil. Zvolíme-li Q0 = -Q/4, budou i výsledné síly působící na náboje Q nulové. Všechny tři náboje jsou tedy v rovnováze.
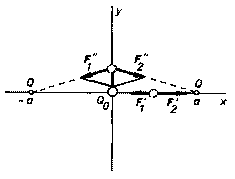
Podobně uvažujme
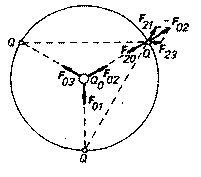
náboj Q0 umístěný ve středu kružnice o poloměru R a n
bodových nábojů Q rozmístěných
symetricky po obvodu této kružnice. Případ n = 3 je znázorněn na obr. 1.6. Opět je
zřejmé, že síly F01,
F02,
F03
působící na centrální náboj se z důvodu symetrie vyruší a vhodnou volbou velikosti
nábojů lze dosáhnout toho, že i síly působící na náboje Q budou nulové. Přirovnáme-li velikost výslednice odpudivých sil
působící na náboj Q ze strany
ostatních obvodových nábojů a přitažlivé síly centrálního náboje, snadno najdeme,
že pro n = 2 musí platit Q0 =- Q/4, pro n = 3
dostaneme Q0 =
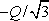 ,
pro n = 4 obdržíme Q0 =
,
pro n = 4 obdržíme Q0 =
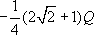 atd.
atd.
Můžeme si položit otázku, jak to bude v případě n (R) yen, tj. je-li možno udržovat náboje spojitě a rovnoměrně rozložené po obvodu kružnice v rovnováze s centrálním nábojem Q0. Označíme-li lineární hustotu nábojů rozložených po obvodu kružnice jako t a budeme hledat odpudivou sílu, kterou působí tyto náboje na malý element náboje kružnice DQ, dostaneme divergující integrál. Centrální náboj, který by měl tuto sílu kompenzovat, by tedy musel mít nekonečnou velikost. Fyzikálně to ovšem znamená pouze to, že idealizace v podobě spojitého náboje rozloženého na nekonečně tenké kružnici není v tomto případě oprávněná.

Vraťme se nyní k otázce charakteru rovnováhy bodových nábojů na obr. 1.5. Podle (1.24) snadno zjistíme, že potenciální energie této soustavy nábojů je rovna nule (a podobně pro případ n = 3, 4,...). Předpokládejme nyní, že se centrální náboj Q0 mírně vychýlí z rovnovážné polohy v kladném směru osy x. Síla, která naň bude v této poloze působit
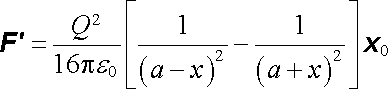 |
(1.26) |
(x0 je jednotkový vektor ve směru osy x), bude výchylku dále zvětšovat - rovnováha tedy byla labilní. Snadno se přesvědčíme, že potenciální energie jako funkce souřadnice x
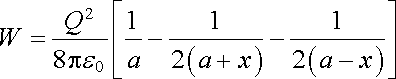 |
(1.27) |
má pro x = 0 maximum.
Vychýlíme-li nyní náboj Q0 z rovnovážné polohy ve směru osy y, bude zřejmě výsledná síla
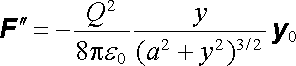 |
(1.28) |
(y0 je jednotkový vektor ve směru osy y) vracet tento náboj do rovnovážné polohy - vzhledem k proměnné y je rovnováha stabilní. Opět můžeme ověřit, že potenciální energie
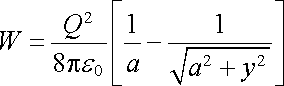 |
(1.29) |
má jako funkce y minimum.
Z uvedeného příkladu jsme viděli, že rovnováha statických bodových nábojů nebyla stabilní. Přesvědčili bychom se o tom i v dalších, složitějších případech. Skutečně platí obecná věta (Earnshawova) o tom, že náboje nelze udržovat ve stabilní rovnováze výhradně elektrostatickými silami (viz články 1.2.5 a 1.4.6).
Určeme elektrostatickou potenciální energii prostorového uspořádání kladných a záporných bodových nábojů, s jakými se setkáváme například u iontových krystalů. Mějme krychli o hraně a jako element kubické mřížky. Ve vrcholech krychle nechť jsou umístěny ionty o náboji -e, ve středu krychle iont o náboji +e (obr. 1.7). Vyčíslíme-li elektrostatickou potenciální energii (1.25) krychle dostaneme

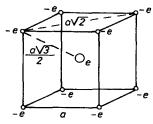
(eq0036)(J). (1.30)
Protože typické vzdálenosti iontů v krystalech jsou v řádu 10-10 m, vidí-me že zjištěná energie je v řádu 10-17 J, tj. asi 100 elektronvoltů (eV) - 1 elektronvolt B 1,602.10-19 J. K určení elektrostatické energie celého krystalu, respektive jeho jednotkového objemu, bychom museli sčítat příspěvky od sousedních a dalších elementů krystalové mřížky, tj. sčítat nekonečné znakoproměnné řady. Proveďme to pro tzv. lineární krystal, tj. rozložení střídavě kladných a záporných nábojů +/-e ve stejných vzdálenostech a podél přímky (obr. 1.8). Zjistíme, že potenciální energie připadající na jeden náboj je
(eq0037)(J), (1.31)
kde veličina a = 2 ln 2 = 1,386 ... se nazývá Madelungova konstanta.

Obr. 1.8 Elektrostatická energie lineárního krystalu.
V případě reálného trojrozměrného iontového krystalu je výpočet numericky obtížný a provádí se na počítačích. Přesto však se výsledné hodnoty elektrostatické energie připadající na jeden iont řádově neliší od hodnoty uvedené ve vzorci (1.31) . Odpovídá to energiím kolem 10 eV typickým pro chemické procesy.
Tak pro krystal chloridu sodného činí Madelungova konstanta 1,747 ..., pro oxid zinečnatý 1,638 ... apod. Všimněme si, že hodnota energie daná výrazem (1.31) je záporná, při zmenšení mřížkové konstanty a klesá, a mělo by proto dojít ke zhroucení krystalu. Neděje se to proto, že v důsledku působení kvantových sil odpuzování na malých vzdálenostech je třeba výraz (1.31) vynásobit faktorem (l - r/a), kde r je experimentálně určovaná kladná konstanta.