Útlum v reálných vlnovodech

Doposud jsme se zabývali ideálními vlnovody s nekonečně vodivými stěnami. To nám umožnilo snadno najít strukturu elektromagnetických vln šířících se vlnovody. Reálný vlnovod, i když jsou jeho stěny dobře vodivé, se od ideálního liší tím, že část energie se ve vodivých stěnách pohltí. Výkon, který protéká určitou rovinou z = konst. není ve všech průřezech stejný, ale se stoupající souřadnicí z klesá. To lze vyjádřit komplexním vlnovým vektorem ve směru z  . Elektromagnetická vlna je tudíž tlumená faktorem . Jde o to, jak tento útlum a určit. 

Všimněme si nejprve velmi prostého případu: rovinná elektromagnetická vlna se šíří vakuem a v rovině z = 0 dopadá na vodivou stěnu vodivosti s (obr. 3.6.1.)

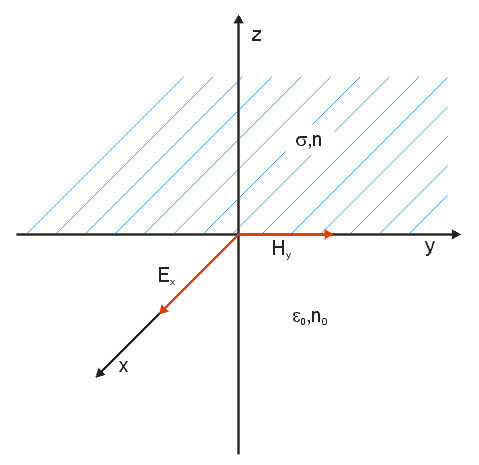
Obr.3.6.1 Rovinná elektromagnetická vlna se šířící se vakuem a v rovině z = 0 dopadající na vodivou stěnu vodivosti s

Zajímá nás magnetické a elektrické pole kovu. Máme:

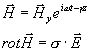
        tj.

            (3.6.1)

        tj.

           (3.6.2)

Z rovnic (3.6.1), (3.6.2) dostaneme

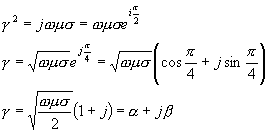
     takže

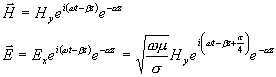
Hloubka skinu se definuje tak, že amplituda v ní klesá na e-tinu původní hodnoty:

Poměr amplitud elektrického a magnetického pole v kovu je:

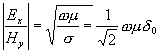
Za jednotku času vnikne do jednotkové plochy kovu z elektromagnetické vlny energie daná Poyntingovým vektorem

V tomto případě

Prakticky důležitý je však střední (nikoliv okamžitý) výkon za jednu periodu

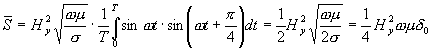          (3.6.3)

(Výraz  se označuje často jako R_f).

Rovnici (3.6.3) můžeme aplikovat na vlnovod tak, že za H_y zvolíme tangenciální složku intenzity magnetického pole na stěně. Nedopustíme se tak velké chyby, budeme-li za tuto složku považovat složku magnetického pole ideálního vlnovodu. Je-li stěna vlnovodu dobře vodivá, liší se oba případy velmi málo. Ztráty ve vodivých stěnách vlnovodu můžeme tedy vyjádřit jako

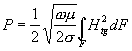          (3.6.4)

kde F je celková plocha přes níž se integruje, H_tg je amplituda tečné složky magnetického pole na stěně.

V této souvislosti poznamenejme, že ve vysokofrekvenční oblasti nás většinou zajímají jen střední časové hodnoty kvadratických veličin, jako je výkon, energie, vystředěné přes periodu vysokofrekvenčních změn. Budeme tyto veličiny značit {A}_T Střední hodnoty { }_T se dají výhodně počítat za použití komplexních amplitud, které se zavedou obdobně jako v symbolické metodě. Např. vektor elektrického pole se symbolicky píše jako

kde indexem 1 označíme, že jde o komplexní amplitudu. Skutečnou hodnotu dostaneme tak, že  vynásobíme vektorem  a vezmeme reálnou nebo imaginární část. Pro takto zvolené komplexní amplitudy se dá snadno dokázat, že střední hodnoty kvadratických veličin se dají vyjádřit pomocí součinů tvarem , kde  je komplexně sdružené číslo k .Střední hodnota elektrické energie obsažená v objemu V je

a podobně pro magnetickou energii platí

Zavádí se též komplexní Poyntingův vektor

          (3.6.5)

a přesvědčíme se, že

          (3.6.6)

Vraťme se nyní k původnímu úkolu - výpočtu útlumu ve vlnovodu s konečnou vodivostí stěn.

Střední tok energie průřezem vlnovodu za jednotku času se dá nyní pomocí (3.6.5) a (3.6.6) vyjádřit jako

,

kde S₀ je plocha průřezu vlnovodu. Vzhledem k vlastnostem pole ve vlnovodu, šíří se vlny ve směru osy z, obecně tlumené: .Ve výrazu  je obsažen faktor , takže derivováním dostaneme

          (3.6.7)

což je úbytek středního výkonu přenášeného vlnovodem na jednotku délky. Ve vlnovodu, který je vyplněn vakuem (nejsou dielektrické ztráty),  je tento úbytek způsoben výkonem pohlceným vodivými stěnami. S použitím (3.6.4) můžeme psát

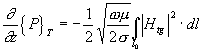          (3.6.8)

kde l₀ je obvod vlnovodové stěny. Spojením výrazů (3.6.7) a (3.6.8) dostáváme pro útlum

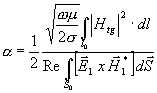          (3.6.9)

Poznámka: místo (3.6.8) bychom mohli též formálně s použitím komplexního Poyntingova vektoru psát

kde  je jednotkový vektor ve směru vnější normály k povrchu (rovnoběžný se složkou Poyntingova vektoru, který směřuje zevnitř vlnovodu do stěny). Vzhledem k tomu, že  představuje tangenciální složku intenzity elektrického pole na stěně vlnovodu a u ideálního vlnovodu je nulová, musíme použít vztah odvozený pro vodič

a dostaneme opět (3.6.9).

Poznámka: rovnice (3.6.9) vyjadřuje útlum v jednotkách označovaných někdy jako Neper / m. Přechod k obvyklým decibelům se provede vynásobením faktorem 8,686 = 20 log ₁₀^e.

Úloha:

Vypočítejte si útlum podle (3.6.9) pro vlnu H₁₀ v obdélníkovém vlnovodu o stranách a, b.

Výsledek: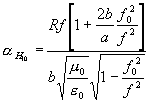    

Obecné vzorce pro útlumy vln H_mn a E_mn v pravoúhlém vlnovodu:

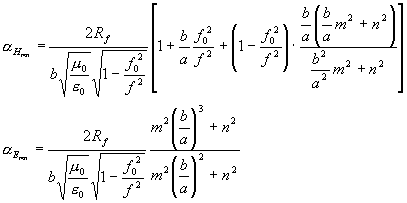
Obdobně se z (3.6.9) dostane útlum ve vlnovodech kruhového průřezu  (je-li a poloměr kruhu):

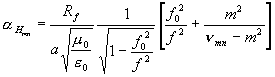
kde  jest kořen čísluje kořeny.

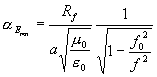
Konečně uveďme ještě útlum pro koaxiální vedení:

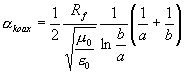
který s frekvencí roste jako .

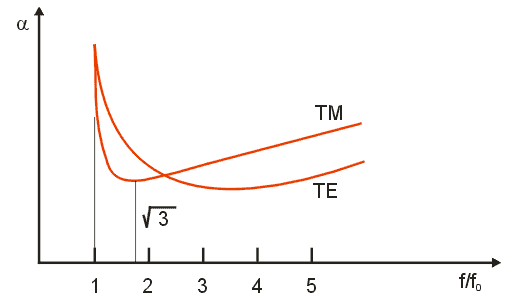
Obr.3.6.2 Typická závislost útlumu na frekvenci pro pravoúhlý vlnovod

Na obr. 3.6.2 je znázorněna typická závislost útlumu na frekvenci pro pravoúhlý vlnovod. Při kritické frekvenci je útlum nekonečný, pak klesá k minimu. To pro vlny TM leží vždy u a pak opět roste.Pro vlny TE je výsledek závislý na geometrických a indexových faktorech. V mikrovlnné oblasti bývá útlum 20-40 dB/km.

<<< předchozí | hlavní stránka | další >>>