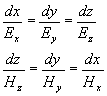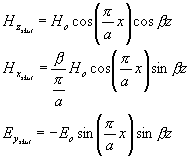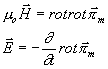Předpokládáme, že elektromagnetická vlna se šíří
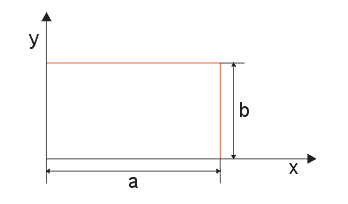
vlnovodem obdélníkového průřezu (obr. 3.2.1) o délce stran a a b.
Protože
rovnice (3.1.5) a (3.1.6) pro podélné složky elektrického a magnetického pole jsou
nezávislé, můžeme i vlny ve vlnovodech rozdělit na transverzálně magnetické
TM
(E), kdy
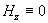 a
transversálně elektrické TE (H), kdy
a
transversálně elektrické TE (H), kdy
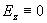 .
.
Vybereme si
vlnu TM v ideálním vlnovodu obdélníkového průřezu, se stranami a,b
(obr. 3.2.1). Rovnici (3.1.5) řešíme obvyklou metodou
separace proměnných. Položíme
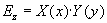 , odkud plyne
, odkud plyne
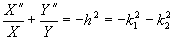
takže
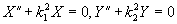
Řešení je typu
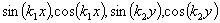 .
. 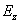 dostaneme
vynásobením obecných řešení rovnic pro X
a Y. Společné řešení nebudeme
vypisovat. Zvolíme takové, které splní podmínky pro ideální vlnovod: tangenciální
složka E na stěnách musí být nulová, takže
dostaneme
vynásobením obecných řešení rovnic pro X
a Y. Společné řešení nebudeme
vypisovat. Zvolíme takové, které splní podmínky pro ideální vlnovod: tangenciální
složka E na stěnách musí být nulová, takže
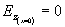 a
a
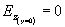 . Ihned vidíme, že vhodné jsou pouze siny, takže
. Ihned vidíme, že vhodné jsou pouze siny, takže
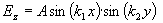 (3.2.1)
(3.2.1)
Dostaneme ještě podmínky pro zbývající dvě stěny
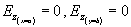
tj.
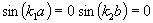
odtud
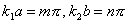 , kde m,n jsou celá čísla
, kde m,n jsou celá čísla
a máme
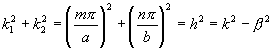
Dosadíme-li
nyní za vlnové vektory
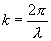 - vztahuje
se k volnému prostoru a
- vztahuje
se k volnému prostoru a
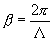 -vztahuje
se k vlnovodu, dostaneme následující výraz
-vztahuje
se k vlnovodu, dostaneme následující výraz
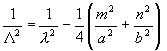 (3.2.2)
(3.2.2)
L je vlnová délka ve vlnovodu, L2 musí být kladné.
Šíření ve vlnovodu je možné jen pro ty vlnové délky l ve volném prostoru,
pro něž platí, že 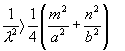
Pro
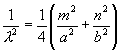 se vlnová délka
L ve vlnovodu stává nekonečnou, šíření vlnovodem přestává. Tato
vlnová délka se nazývá kritická a platí pro ni vztah
se vlnová délka
L ve vlnovodu stává nekonečnou, šíření vlnovodem přestává. Tato
vlnová délka se nazývá kritická a platí pro ni vztah
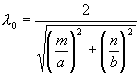 (3.2.3)
(3.2.3)
Všechny
vlnové délky, které jsou ve volném prostoru delší než kritické se vlnovodem
šířit nemohou. Kritické vlnovodové délce odpovídá kritická frekvence
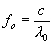 . Vyjádříme-li vlnovou délku ve vlnovodu
L pomocí frekvence signálu, dostaneme vztah
. Vyjádříme-li vlnovou délku ve vlnovodu
L pomocí frekvence signálu, dostaneme vztah
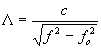 z čehož je patrné,
že vlnovod je disperzní prostředí (vlnová délka závisí na frekvenci). Dále
pro fázovou rychlost šíření vln ve vlnovodu platí
z čehož je patrné,
že vlnovod je disperzní prostředí (vlnová délka závisí na frekvenci). Dále
pro fázovou rychlost šíření vln ve vlnovodu platí
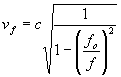 a pro grupovou
rychlost
a pro grupovou
rychlost
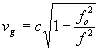 .
.
Pro vlny TE
(H) platí obdobně
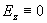 .
Složky polí dostaneme řešením rovnice (3.1.6) včetně
okrajových podmínek a výpočtem podle (3.1.7) až
(3.1.10). Pro ideální vodič platí,
že normálové složky intenzity magnetického pole na vodiči jsou nulové. Podle
obr. 3.2.1 je
.
Složky polí dostaneme řešením rovnice (3.1.6) včetně
okrajových podmínek a výpočtem podle (3.1.7) až
(3.1.10). Pro ideální vodič platí,
že normálové složky intenzity magnetického pole na vodiči jsou nulové. Podle
obr. 3.2.1 je
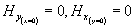
Vzhledem k tomu, že
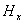 ~
~
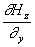 a
a
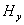 ~
~
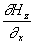 , pak při obdobném postupu jako při řešení rovnice
(3.1.5) vyhovují
těmto okrajovým podmínkám cosiny, takže dostaneme
, pak při obdobném postupu jako při řešení rovnice
(3.1.5) vyhovují
těmto okrajovým podmínkám cosiny, takže dostaneme
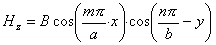 (3.2.4)
(3.2.4)
Pro
kritickou vlnovou délku dostaneme opět výraz (3.2.3). Celá čísla m,n se nazývají indexy a
označují vid (modus) příslušné vlny. Vlna se označuje takto:
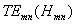 nebo
nebo 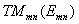 .
.
Pro vlnu
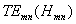 dostaneme netriviální
výsledek i při jednom indexu nulovém. Pro vlnu
dostaneme netriviální
výsledek i při jednom indexu nulovém. Pro vlnu
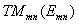 nemůže být vzhledem k
(3.2.2) ani jeden index nulový a nejnižší vid má
nemůže být vzhledem k
(3.2.2) ani jeden index nulový a nejnižší vid má
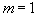 a
a
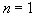 . Pomocí indexů se značí i kritické vlnové délky jako
. Pomocí indexů se značí i kritické vlnové délky jako
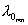 . Vlny typu
H a E mají při shodných indexech stejnou
kritickou vlnovou délku, avšak příslušné vlny se svou strukturou liší. Jedna
vlna, která se může šířit ve vlnovodu obdélníkového průřezu má kritickou
vlnovou délku největší. Jestliže je
. Vlny typu
H a E mají při shodných indexech stejnou
kritickou vlnovou délku, avšak příslušné vlny se svou strukturou liší. Jedna
vlna, která se může šířit ve vlnovodu obdélníkového průřezu má kritickou
vlnovou délku největší. Jestliže je
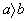 (obr.
3.2.1), jedná se o vlnu
(obr.
3.2.1), jedná se o vlnu
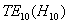 a její kritická vlnová délka
a její kritická vlnová délka
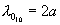 .
.
Pro zjednodušení úvah budeme uvažovat specielní případ
vlnovodu čtvercového průřezu, tj.
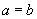 . Nyní můžeme snadno seřadit vidy podle kritických vlnových
délek:
. Nyní můžeme snadno seřadit vidy podle kritických vlnových
délek:
|
vid |
l0 |
|
H10 , (H01) |
2a |
|
H11, E11 |
1, 413a |
|
H20, (H02) |
a |
|
H12, E12 |
0, 846a |
|
H22, E12 |
0, 718a |
|
H30, (H03) |
0, 666a |
|
H13, E13 |
0, 632a |
|
H23, E23 |
0, 554a |
|
H40, (H04) |
0, 500a |
|
. |
. |
|
. |
. |
|
. |
. |
Se stoupajícími hodnotami indexů klesá kritická vlnová
délka. Můžeme si tento výsledek znázornit takto (obr. 3.2.2).
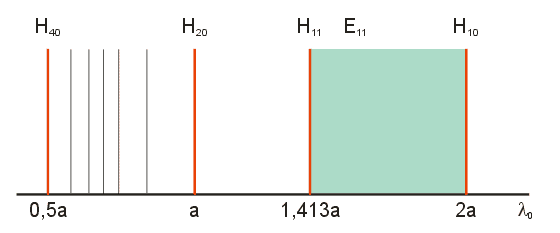
Obr.3.2.2 Závislost vlnové délky na indexu
Směrem doleva od kritické vlnové délky se mohou šířit vlny,
které jsou kratší. Z toho plyne, že v barevné oblasti (mezi l =
2a a l = 1,413a) se může šířit pouze vlna
H10, která má nejdelší kritickou vlnovou délku, (vlna
dominantní). To má důležitý praktický význam. V ostatních oblastech se mohou
šířit všechny vidy, pro něž l leží nalevo od jejich
kritické vlnové délky a je třeba speciálních opatření, aby se mohl šířit jen
žádoucí vid.
Strukturu pole ve vlnovodu pravoúhlého průřezu dostaneme z rovnic pro složky pole např. z rovnice
(3.2.4). Skutečné
hodnoty pole získáme vynásobením složky výrazem
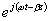 .
Vezmeme reálnou
nebo imaginární část. Z rovnice (3.2.4) tedy máme
.
Vezmeme reálnou
nebo imaginární část. Z rovnice (3.2.4) tedy máme
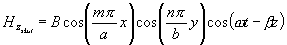
a obdobné výrazy stejným postupem pro ostatní složky z
rovnic (3.1.7) až (3.1.10). Je obvyklé znázorňovat průběhy elektromagnetických
polí ve vlnovodech pomocí „siločar“ (podobně jako v elektrostatice nebo
magnetostatice). To znamená, že si zvolíme určitý čas (např.
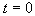 ) a v tomto okamžiku „pořídíme“ záběr siločar, obecně řešením
rovnic
) a v tomto okamžiku „pořídíme“ záběr siločar, obecně řešením
rovnic
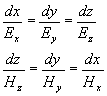
Pro vlnu H10 a pro t
= 0 dostaneme:
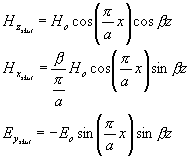
kde
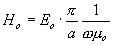
a
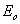 je
intenzita y-ové
(a v tomto případě jediné) složky elektrického pole pro
je
intenzita y-ové
(a v tomto případě jediné) složky elektrického pole pro
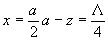 (resp.
(resp.
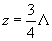 ). Siločáry elektrického pole mají směr osy
y,magnetické siločáry jsou stejné ve všech rovinách XZ a jsou
vyjádřeny rovnicemi
). Siločáry elektrického pole mají směr osy
y,magnetické siločáry jsou stejné ve všech rovinách XZ a jsou
vyjádřeny rovnicemi
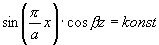
| Vlna TE10 |
| Siločáry:
1 - v rovině xz
2 - v rovině yz
3 - v rovině xy |
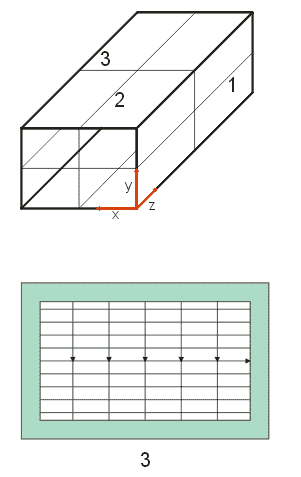 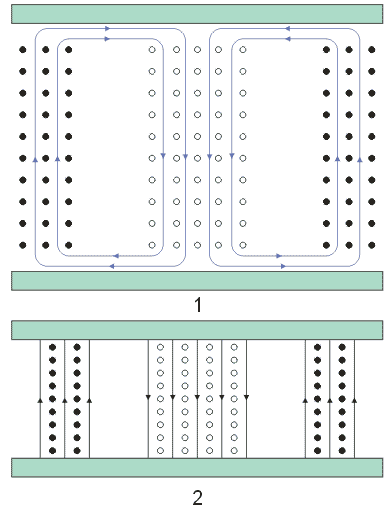 |
| Nenulové složky pole |
Hz, Hx, Ey |
| l0 |
2a |
Obr.3.2.3 Vlna TE10
| Vlna TE11 |
| Siločáry:
1 - v rovině xz
2 - v rovině yz
3 - v rovině xy |
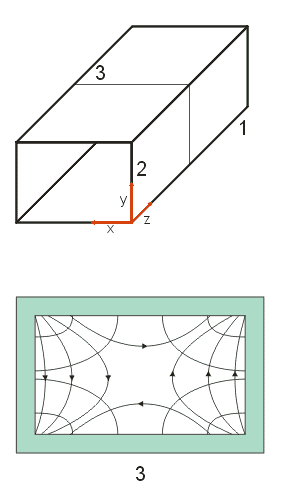 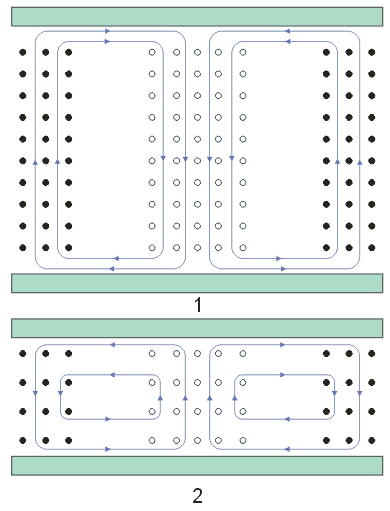 |
| Nenulové složky pole |
Hz, Hx, Hy,
Ex, Ey |
| l0 |
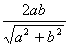 |
Obr.3.2.4 Vlna TE11
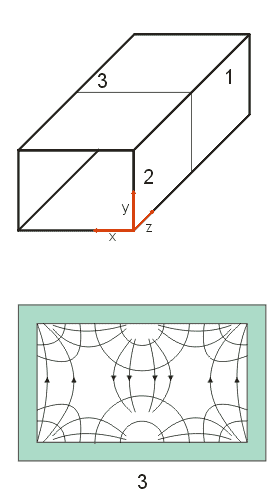
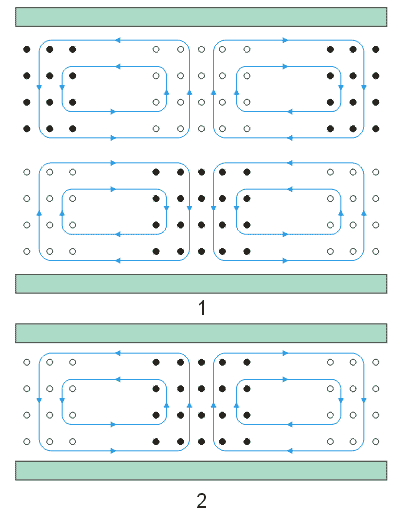
| Vlna TE21 |
| Siločáry:
1 - v rovině xz
2 - v rovině yz
3 - v rovině xy |
  |
| Nenulové složky pole |
Hz, Hx, Hy,
Ex, Ey |
| l0 |
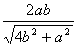 |
Obr.3.2.5 Vlna TE21
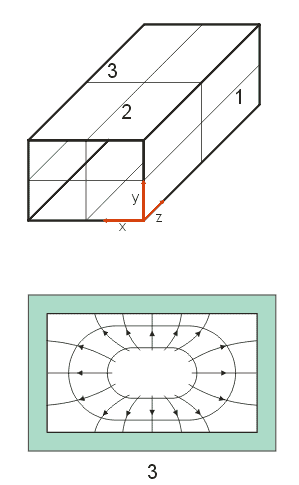
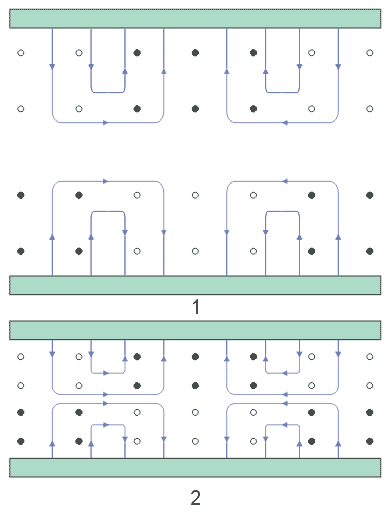
| Vlna TM11 |
| Siločáry:
1 - v rovině xz
2 - v rovině yz
3 - v rovině xy |
  |
| Nenulové složky pole |
Ez, Ex, Ey,
Hx, Hy |
| l0 |
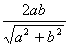 |
Obr.3.2.6 Vlna TM11
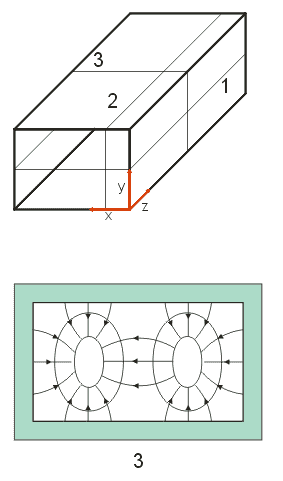
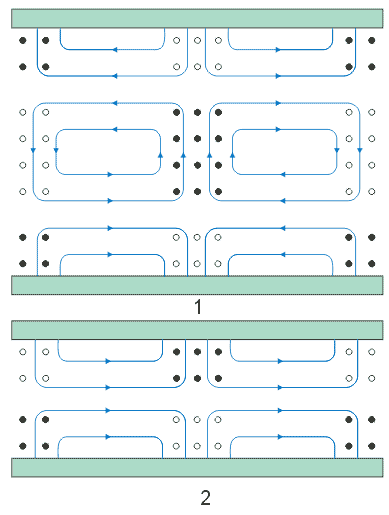
| Vlna TM21 |
| Siločáry:
1 - v rovině xz
2 - v rovině yz
3 - v rovině xy |
  |
| Nenulové složky pole |
Ez, Ex, Ey,
Hx, Hy |
| l0 |
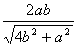 |
Obr.3.2.7 Vlna T21
Podobným způsobem lze získat představu o struktuře pole v
obdélníkovém vlnovodu i u vyšších vidů. Na obr. 3.2.3 až 3.2.7 jsou znázorněny vlny
TE10,TE11,TE21,TM11,TM21
a charakteristické údaje (l0a nenulové složky pole).
Poznámka: někdy se používají místo vektorů
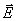 a
a
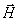 ve vlnovodech
Hertzovy vektory
ve vlnovodech
Hertzovy vektory
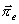 a
a
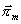 (elektrický a
magnetický). Elektrický Hertzův vektor souvisí s vektorovým potenciálem
(elektrický a
magnetický). Elektrický Hertzův vektor souvisí s vektorovým potenciálem
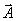 vztahem
vztahem
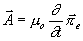
takže
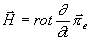
a
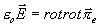
Vektor
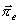 vyhovuje vlnové
rovnici
vyhovuje vlnové
rovnici
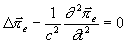
a na povrchu ideálního vodiče platí
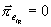 .
.
Magnetický Hertzův vektor
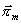 je dán vztahy
je dán vztahy
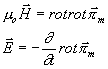
a splňuje vlnovou rovnici stejnou jako
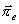 . Na povrchu ideálního vodiče
je
. Na povrchu ideálního vodiče
je
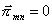 . Elektromagnetická pole popsaná vektory
. Elektromagnetická pole popsaná vektory
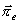 a
a
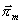 nejsou stejná, jedním
z obou vektorů nelze vyjádřit všechna řešení. Pomocí elektrického vektoru
nejsou stejná, jedním
z obou vektorů nelze vyjádřit všechna řešení. Pomocí elektrického vektoru
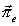 lze ve vlnovodu
popsat vlny TM(E). Dá se ukázat, že platí
lze ve vlnovodu
popsat vlny TM(E). Dá se ukázat, že platí
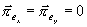 avšak
avšak
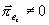 a to jest
a to jest
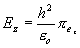 . Obdobně pro vlny TE(H) vyjádřené pomocí Hertzova
magnetického vektoru
. Obdobně pro vlny TE(H) vyjádřené pomocí Hertzova
magnetického vektoru
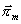 platí
platí
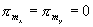 a
a
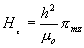 .
.
V tomto pojednání nebudeme používat Hertzovy vektory. Jejich
praktický význam tkví v tom, že vhodně formalizují dva způsoby buzení
elektromagnetických vln - pomocí elektrického dipólu (antény) nebo pomocí magnetického
dipólu (závitu protékaného proudem). To jsou však problémy zasahující za rámec
našich cílů. V literatuře věnované vlnovodům se však můžete s
formalizmem
používajícím Hertzovy vektory setkat.
<<< předchozí | hlavní stránka | další >>>
![]() ). Tento předpoklad prakticky nemůže být splněn,
ale
značně zjednoduší okrajové podmínky - v nekonečně vodivém obalu vlnovodu
je
tangenciální složka elektrického pole nulová, právě tak jako normálová složka
magnetického pole. Současně, ve vlnovodu vyplněném vakuem a s ideálně vodivými
stěnami nenastávají žádné tepelné ztráty a útlum
). Tento předpoklad prakticky nemůže být splněn,
ale
značně zjednoduší okrajové podmínky - v nekonečně vodivém obalu vlnovodu
je
tangenciální složka elektrického pole nulová, právě tak jako normálová složka
magnetického pole. Současně, ve vlnovodu vyplněném vakuem a s ideálně vodivými
stěnami nenastávají žádné tepelné ztráty a útlum
![]() , takže
, takže
![]() je čistě
imaginární, a
je čistě
imaginární, a
![]()
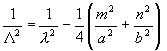 (
(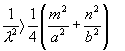
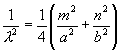 se vlnová délka
L ve vlnovodu stává nekonečnou, šíření vlnovodem přestává. Tato
vlnová délka se nazývá kritická a platí pro ni vztah
se vlnová délka
L ve vlnovodu stává nekonečnou, šíření vlnovodem přestává. Tato
vlnová délka se nazývá kritická a platí pro ni vztah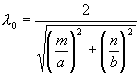 (
(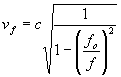 a pro grupovou
rychlost
a pro grupovou
rychlost
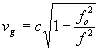 .
.