.
Vlnovody jsou válcová dielektrická tělesa, jejichž plášť je tvořen dobře vodivým materiálem. Budeme se zabývat vlnovody, jejichž průřez má jednoduchý tvar a je snadno vyrobitelný. Jsou to vlnovody s obdélníkovým a kruhovým průřezem. V dalším se ukáže, že na rozdíl od elektromagnetických vln, které se šíří ve volném prostoru (dielektriku nebo vakuu) mají vlny ve vlnovodu i podélnou složku elektrického nebo magnetického pole.
Z tohoto důvodu se používá následující označení:
- vlny, které mají pouze příčné složky polí (jako ve volném prostoru), se označují jako vlny transverzálně elektromagnetické - TEM
- vlny, které mají podélnou složku elektrického pole se označují jako vlny transverzálně magnetické - TM nebo též jako vlny elektrické - E
- vlny s podélnou složkou magnetickou se označují jako vlny transverzálně elektrické - TE nebo jako vlny magnetické - H
Bude nás zajímat, jaké vlny se mohou vlnovodem šířit. To ovšem neznamená, že v každém konkrétním případě se jím šíří. To záleží též na tom, jakým způsobem se bude přivádět do vlnovodu energie a dalších okolnostech, což je podstatně složitější.
Předpokládáme, že vlnovod je vyplněn
vakuem (prakticky též vzduchem atmosférického tlaku,
neboť rozdíl v permitivitách je zanedbatelný), a že
uvnitř vlnovodu nejsou žádné náboje a neteče
tam vodivostní proud tj. .
Maxwellovy rovnice pro tento případ mají tvar
(3.1.1)
(3.1.2)
(3.1.3)
(3.1.4)
Za směr šíření, který je totožný s osou vlnovodu, zvolíme osu z a předpokládáme, že s časem se pole mění sinusově. Pak můžeme položit
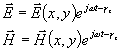
a skutečné hodnoty pole dostaneme jako
(případně
).
g je obecně komplexní konstanta
šíření 
,
neboť elektromagnetická vlna šířící se vlnovodem může být i tlumená, dochází-li ke ztrátám (např. tepelné
ztráty ve
stěnách s konečnou vodivostí).
Položíme-li 
vidíme, že
a je útlum a 
je vlnový vektor (má dle
předpokladu jen z-tovou složku), v je fázová rychlost ve vlnovodu a
L je vlnová délka
příslušná frekvenci w ve vlnovodu.
Za předpokladu, že ve směru osy z se šíří tlumená sinusová vlna dostaneme z rovnic (3.1.1) až (3.1.4):
|
|
(3.1.1´)
|
|
(3.1.2´)
|
|
|
(3.1.3´)
|
|
| (3.1.4´) |
Rozepsáním rovnic pro rotace (3.1.1´) a (3.1.2´) dostaneme šest rovnic. Ty lze upravit následujícím způsobem: x-ové a y-ové složky se dají vyjádřit pomocí derivací z-ových složek a pro z-ové složky dostaneme vlnové rovnice.
Vezměme např.: 
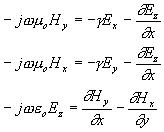
První z těchto rovnic derivujeme parciálně podle x, druhé podle y, dosadíme tyto výrazy do třetí rovnice a vezmeme v úvahu, že podle (3.1.3´)
.
Dostaneme
ale
kde c je fázová rychlost ve volném prostoru vakua, k je vlnový vektor ve volném prostoru a l příslušná vlnová délka vztahující se k frekvenci w ve volném prostoru. Zavedeme ještě označení
a dostaneme vlnovou rovnici pro z-ovou tj. podélnou složku elektrického pole ve tvaru
(3.1.5)
Analogickým postupem bychom dostali obdobnou rovnici pro podélnou složku magnetického vektoru
(3.1.6)
Pro transversální složky pak dostaneme z rovnic vhodnou úpravou tyto vztahy:
(3.1.7)
(3.1.8)
(3.1.9)
(3.1.10)
Je vidět, že řešením rovnic (3.1.5) a (3.1.6)pro podélné složky dostaneme vše, co
potřebujeme. Transverzální (příčné) složky získáme z rovnic
(3.1.7) až (3.1.10) derivováním.
Všimněme si, že je to však možné jen tehdy, jestliže
. Dále je
třeba si uvědomit, že řešení rovnic (3.1.5) a(3.1.6) má význam
pouze tehdy, jsou-li
určeny okrajové podmínky. Zatím jsme předpokládali, že elektromagnetická vlna se
šíří ve směru osy z, vakuem, kde nejsou náboje ani vodivé proudy.
