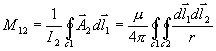Sítě a obvody s rozloženými parametry
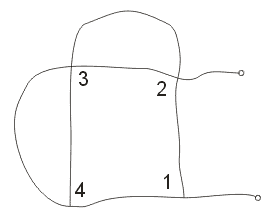 |
Zatím jsme zkoumali pouze obvod složený z jediné smyčky. V případě sítě
(obr.1.7.1) se nám integrál
(1.5.6) rozpadne do
čtyř integrálů podél jednotlivých větví. Pro každou větev pak můžeme spočítat vnitřní impedanci, vnější indukčnost a kapacitu podle
dříve uvedených vzorců.
V celé větvi přepokládáme konstantní proud.
Jinak řečeno dosud uvažovaný a navrhovaný postup nebral do úvahy možnost, že proud jednou větví sítě může být ovlivňován proudem v jiné větvi sítě.
Pokud tomu tak není, můžeme k řešení obvodu použít Kirchhoffovy zákony případně nějakou příbuznou metodu
- obvodové proudy, uzlové napětí ....
|
Obr. 1.7.1 Síť -
obvod z více smyček
|
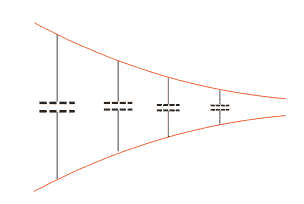 |
Pokud máme obvod s rozloženými parametry (obr.1.7.2), můžeme tento obvod převést na síť tak,
že aproximujeme rozložené parametry řadou soustředěných parametrů
⇒ obvod převedeme do tvaru sítě. Tato aproximace může být provedena až do úrovně
infinitezimálních soustředěných parametrů a v určitých případech může příslušný systém,
např. homogenní vedení, popisovat s dostatečnou přesností.
Pokud však užíváme velmi vysokých kmitočtů, bývá velmi obtížné tyto soustředěné aproximativní parametry určit.
Pak je nutné řešit Maxwellovy rovnice s příslušnými okrajovými podmínkami.
|
Obr. 1.7.2
Obvod s rozloženými parametry
|
Všimněme si ještě vzájemné indukčnosti v nízkofrekvenčních obvodech.
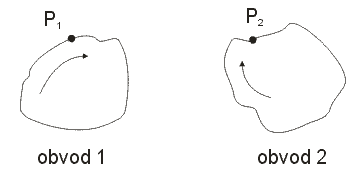 |
Mějme dvě smyčky
(obr.1.7.3). Pokud proud obvodu 1 indukuje nezanedbatelné pole v obvodu 2 a naopak, má indukované elektrické pole v bodě (např.) P1 dvě
složky - jedna vzniká díky proudu I1 v obvodu 1 druhá díky proudu
I2 v obvodu 2.
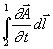 je
Induktivním členem v rovnici
(1.5.6). je
Induktivním členem v rovnici
(1.5.6).
Pak druhá složka: 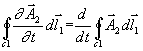 .
.
|
Obr. 1.7.3 Dva nízkofrekvenční
obvody - smyčky
|
Vektorový potenciál
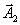 lze napsat jako
lze napsat jako 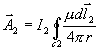 , neboť proud je nenulový a konstantní jen podél křivky c2.
, neboť proud je nenulový a konstantní jen podél křivky c2.
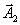 je úměrné
I2 přes konstantu, která je funkcí konfigurace
obvodu:
je úměrné
I2 přes konstantu, která je funkcí konfigurace
obvodu: 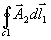 ~
I2.
~
I2.
Je možné zavést konstantu úměrnosti 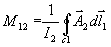
Napětí indukované v obvodu 1 změnou proudu v obvodu 2 je dáno:
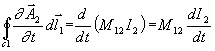 . To je již obvyklý člen popisující vzájemnou indukčnost v klasické teorii obvodů.
. To je již obvyklý člen popisující vzájemnou indukčnost v klasické teorii obvodů.
Aplikací Stokesovy věty získáme další výraz pro M12:
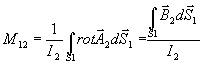 ⇒M12 je magnetický tok procházející obvodem 1 (jeho plochou)
vybuzený proudem v obvodu 2 na jednotku proudu v obvodu 2.
⇒M12 je magnetický tok procházející obvodem 1 (jeho plochou)
vybuzený proudem v obvodu 2 na jednotku proudu v obvodu 2.
Další vzorec pro
M12 dostaneme dosazením formule pro
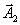 do vztahu pro
M12:
do vztahu pro
M12:
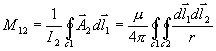 ,
,
což je Neumannův tvar pro vzájemnou indukčnost obvodů složených z tenkých vodičů. Je zřejmé, že
M12 je funkcí jen geometrie obvodů, nikoliv proudů. Dále je zřejmé, že
M12 = M21.
<<< předchozí | hlavní stránka
| další >>>



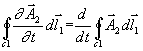 .
. 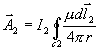 , neboť proud je nenulový a konstantní jen podél křivky c2.
, neboť proud je nenulový a konstantní jen podél křivky c2.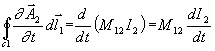 . To je již obvyklý člen popisující vzájemnou indukčnost v klasické teorii obvodů.
. To je již obvyklý člen popisující vzájemnou indukčnost v klasické teorii obvodů.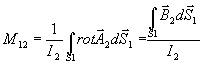 ⇒M12 je magnetický tok procházející obvodem 1 (jeho plochou)
vybuzený proudem v obvodu 2 na jednotku proudu v obvodu 2.
⇒M12 je magnetický tok procházející obvodem 1 (jeho plochou)
vybuzený proudem v obvodu 2 na jednotku proudu v obvodu 2.