Pokud se vrátíme ke vzorci pro komplexní amplitudu napětí na přenosovém vedení a spočítáme z ní skutečné hodnoty napětí např. pro případ zakončení charakteristickou impedancí, zjistíme, že , kde . Jedná se o  jednorozměrnou analogii šíření vln v prostoru. Tato analogie není náhodná, její opodstatnění vyplyne z řešení Maxwellových rovnic pro vlnovody.

Nejprve zopakujeme šíření elektromagnetických vln ve vakuu a v prostředí a zavedeme Poyntingův vektor.

Vyjdeme z rotačních Maxwellových rovnic:

      ,      .

První rovnici vynásobíme druhou a odečteme je od sebe. Dostaneme:

.

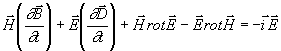Pokud bude závislost na a na lineární, tj. (je tenzor permitivity, ne Levi-Civitův tenzor) je možné napsat .

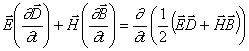Dále platí a pokud zavedeme Poyntingův vektor (označení je z německého Strahlungs vektor - vektor záření - viz [3] str. 120 a dále) můžeme napsat rovnici . Všechny členy mají rozměr J.s^-1 . Jedná se o bilanční rovnici energie. Výraz představuje Jouleovské teplo vytvořené v objemové jednotce vodivého prostředí za jednotku času.

Hustota energie elektromagnetického pole je .

Smysl Poyntingova vektoru můžeme ozřejmit, přepíšeme-li naši bilanční rovnici pro vakuum (σ = 0) tj. . Integrujeme přes určitý objem V a použijeme Gaussovu větu:

(první je Poyntingův vektor, druhé je element plochy).

Poyntingův vektor je vektorem proudové hustoty elektromagnetické energie. Tento důkaz podává pouze informaci, že celkový úbytek energie z oblasti za jednotku času je dán integrálem . Poyntingův vektor nás informuje o změnách a velikostech toku energie v každém místě prostoru. 

Mějme například válcový vodič, kterým teče proud I_z.

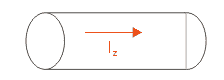	Pokud označíme R odpor na jednotku délky, bude pak pole Ez dáno výrazem (Ohmův zákon). Magnetické pole na povrchu vodiče (resp. v libovolné vzdálenosti r od  vodiče) je . Poyntingův vektor směruje tedy radiálně do vodiče:    ,   .
Obr. 1.12.1 Válcový vodič

Spočítáme-li energii vnesenou tímto vektorem za 1s do vodiče integrací přes válec o poloměru vodiče a délce 1m, dostaneme výkon

, který se rovná výkonu disipovanému Jouleovským teplem. Podle této představy baterie vytváří elektrické a magnetické pole. Energie teče tímto polem přes povrch vodiče do vodiče.

Pro stacionární střídavý případ se používá komplexní Poyntingův vektor, který udává střední hodnotu reálného Poyntingova vektoru za jednu periodu:

              , kde * udává komplexní sdruženost.

V souvislosti s energií elektromagentického pole je vhodné si uvědomit, že elektromagnetické pole nese i hybnost a moment hybnosti, takže elektromagnetické pole může působit i mechanickými účinky - ponderomotivní účinky elektromagnetického pole. Například v tokamacích se v poslední době užívá ohřev na dolnohybridním kmitočtu. To je de facto využití ponderomotivních účinků pole pro urychlení částic podél křivek magnetického pole v tokamaku, čímž zpětně dochází ke zvyšování energie v jednotce objemu plazmatu.

Zatím jsme odvozovali rovnice pro a φ v nevodivém prostředí a v kvazistacionárním případě ve vodiči, kdy jsme zanedbávali posuvný proud proti proudu vodivostnímu.

Nyní odvodíme rovnice pro a pro obecný případ, kdy budeme uvažovat vodivostní a posuvný proud (viz [3] str.135). Předpokládáme lineární matematické vztahy:

      ,           ,     

 a vyjdeme z rotačních rovnic:

      ,     .

Na první rovnici užijeme operátor rot a dosadíme ze druhé rovnice:

.

V homogenním prostředí je a tedy pravá strana rovnice je rovna 0.

Obdobně aplikací rotace na druhou rovnici a po úpravě:

.

Kvazistacionární případ pak můžeme charakterizovat jako „pomalu se měnící pole“. Druhé derivace jsou mnohem menší než první derivace podle času:

      ,      .

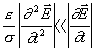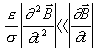Nerovnosti lze dosáhnout buď  „nízkým“ kmitočtem nebo velkou vodivostí.

V tomto případě lze “vypustit” členy obsahující druhé derivace z odvozených rovnic. V opačném případě, platí obrácení „silné“ nerovnosti, což je dáno většinou nevodivým prostředím σ → 0, dostáváme vlnové rovnice, které první derivace a podle času neobsahují. Nás bude především zajímat případ harmonických časových závislostí:

      ,      ,

což vede k Helmholzově rovnici:

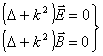  , kde   ,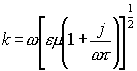  

Pro ωt << 1 dostaneme kvazistacionární přiblížení (difuze pole k povrchu vodiče), pro ωt → ∞ (malé  σ) dostaneme řešení ve tvaru rovinné vlny šířící se rychlostí , kde je relativní index lomu prostředí.

Obecně lze řešení vlnové rovnice v nevodivém prostředí psát ve tvaru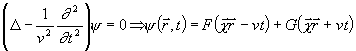 (viz [3] str.138 a dále) . je jednotkový vektor ve směru šíření vlny, je fázová rychlost vlny, N je obecně funkcí kmitočtu N = N(ω).

Z analýzy řešení plyne, že každé nestatické řešení vyhovující Maxwellovým rovnicím se skládá pouze z příčných (transverzálních) komponent. Vektory a jsou rovnoběžné s rovinou kolmou na . Stočíme-li souřadnou soustavou tak, že směr šíření bude totožný s osou z, soustava Maxwellových rovnic se nám podstatně zjednoduší. Předpokládejme dále, že derivace podle x a y jsou nulové. Rozebíráme tedy případ, kdy jediné změny a nastávají ve směru z. Pak dostaneme z rotačních Maxwellových rovnic

      a       

tyto rovnice:

Rovnice s nulou na levé straně potvrzují naše dřívější zjištění, že nestatické řešení nemá z-ovou složku. Řešení pro E_x ,E_y , H_z , H_y se dají napsat jako součet funkcí argumentu a . Vezmeme-li například pouze složku E_x postupující v kladném směru osy z:, pak .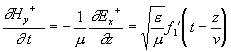

Po integraci podle času a zanedbání konstantní komponenty:

 , kde .

Veličina η má rozměr Ω a nazývá se vlastní impedancí média. Pro vakuum má hodnotu .

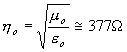Obdobnými úpravami bychom dostali

.

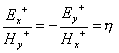
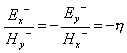Ze skalárního součinu . =0 plyne, že vektory a jsou na sebe kolmé. Z vektorového součinu x , dostaneme vektor v kladném směru osy z (opačně pro x ). Spočítáme-li energii elektrického pole a magnetického pole zjistíme, že U_E = U_H , takže hustota energie v každém bodě a v každém okamžiku je rovnoměrně rozložena mezi elektrické a magnetické pole. Poyntingův vektor směřuje v kladném směru osy z. Časová střední hodnota Poyntingova vektoru musí být stejná ve všech rovinách podél vlny. Lišit se však mohou okamžité hodnoty podle toho, zda dochází ke vzrůstu nebo úbytku energie mezi těmito rovinami.

 Rovinná vlna je tedy charakterizována těmito vlastnostmi :

• Rychlost šíření
• Složky pole ve směru šíření jsou nulové
• Elektrické pole je kolmé na magnetické pole ( ⊥ ) 
• V každém okamžiku je velikost elektrického pole η - krát větší než velikost magnetického pole
• Směr šíření je dán směrem vektorového součinu  x
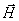
• Energie elektrického pole na jednotku objemu je v každém okamžiku rovna energii magnetického pole v témž okamžiku a bodě
• Okamžité hodnoty Poyntingova vektoru jsou dány , kde E, H jsou okamžité hodnoty intenzit elektrického a magnetického pole

Z hlediska použití mají zejména význam vlny, jejichž argument se harmonicky mění. Zkoumejme takovou monochromatickou vlnu. Pokud směr šíření není totožný s jednou z os, je možné zavést proměnnou , kterou převedeme vlnovou rovnici na v podstatě jednorozměrný případ (viz [3] str. 139). Stačí proto uvažovat, že se vlna šíří podél osy z.

Řešení vlnové rovnice napíšeme ve tvaru:

           (1.12.1)

Případně ještě pomocí komplexních amplitud , kde je vlnové číslo (vlnočet) . Na k je možné nahlížet jako na charakteristiku vlny, neboť udává změnu fáze vlny na 1m šíření. Spíše se však nahlíží na k jako na konstantu prostředí, neboť je možné napsat , kde N je index lomu prostředí.

Pro složku H_y je možné napsat:     .

Okamžitou hodnotu udává reálná část vztahu (1.12.1). Postupné opakování se děje po vzdálenosti .

Střední hodnota Poyntingova vektoru: 

.

 Pokud vlna pochází z jednoho zdroje případně z několika zdrojů s konstantním fázovým rozdílem, můžeme pro řešení vlnové rovnice napsat:

       ,      .

Tyto vektory a budou obecně komplexní. Kvadráty a budou také komplexní. Například s fází -2α:  .

 Zavedeme-li vektor fázově posunutý vůči o úhel -α tj., bude reálné a bude mít stejnou velikost jako . Pak .

Vektor rozložíme na reálnou a imaginární složku, tj. , kde jsou reálné. Platí, že a oba vektory jsou kolmé ke směru šíření.

Pro pak platí:

kde

.

Platí tedy 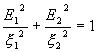. Vektor rotuje v rovině kolmé na směr šíření vlny a jeho konec obecně opisuje elipsu. Taková vlna se nazývá elipticky polarizovaná. Je-li , je vlna kruhově polarizovaná. Je-li nebo nulové, pak pole vlny je v každém okamžiku a místě paralelní jednomu směru, vlna je lineárně polarizovaná. Vektor magnetického pole se chová podobně. Vztahy mezi E_i a H_j lze získat pomocí impedance η.

Pokud má vlna stále konstantní amplitudu, nemůže pomocí ní přenášet informaci. Informaci je možné přenášet, měníme-li amplitudu, frekvenci nebo fázi vlny. Taková vlna pak bude superpozicí rovinných monochromatických vln o různé amplitudě, kmitočtu a fázi.

Předpokládejme opět jednorozměrné přiblížení . Jedním z řešení bude , kde .

V obecném prostředí (nikoliv homogenním) může být , kde nemusí být lineární funkce. Obecné řešení lze pak napsat jako superpozici individuálních monochromatických vln s různou amplitudou . Změny fáze neuvažujeme. Lze ukázat, že složení vln s různou fází dá stejný výsledek jako složení vln s různou frekvencí: . Budeme předpokládat, že vlna ψ je superpozicí vln, jejichž vlnočty leží v úzkém intervalu (viz [3] str.148) a že amplitudy se v tomto intervalu nemění, tj. , pak .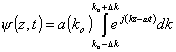

Disperzní závislost linearizujeme a zavedeme .

Argument v integrandu je  .

Výsledné , kde je amplituda „vlnového balíku“ .

Místa stejné amplitudy „balíku“ se pohybují prostorem rychlostí  , kde V se nazývá grupová rychlost.

Označíme-li , můžeme napsat, že amplituda „balíku“ bude nenulová v úzké oblasti, kde . Zvyšujeme-li šířku pásma (), můžeme „balík“ lépe prostorově lokalizovat. Vztah mezi v a V dostaneme ze vztahu  , budeme-li derivovat podle ω:

neboť N je neklesající funkcí kmitočtu .

<<< předchozí | hlavní stránka | další >>>