Skin efekt je jev, při kterém vznikají proudy na povrchu vodiče, který je přivrácen ke zdroji elektromagnetické energie - zdroji pole. V důsledku toho se při vedení vysokofrekvenční energie vodičem soustřeďuje proudová hustota do tenké vrstvy při povrchu vodiče. Například v rezonátoru je proud soustředěn při jeho vnitřních stěnách.

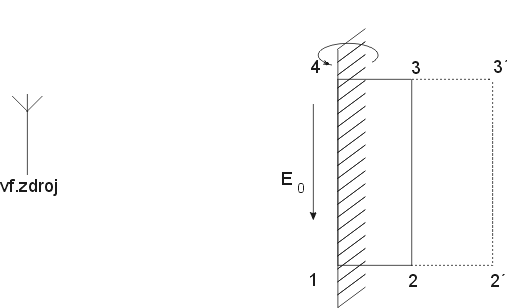
Obr. 1.10.1 Ilustrace k následující úvaze

Princip lze vysvětlit následující úvahou.

Vysokofrekvenční zdroj vytváří paralelně s povrchem elektrické pole . Ve vodiči teče proud a vytváří magnetické pole kolmé  na elektrické pole . Toto magnetické pole indukuje kolmé elektrické pole . je opačného směru než .

Vypočítáme-li křivkové integrály podél křivek 1-2-3-4 a 1-2´-3´-4, zjistíme, že větší magnetický tok je uzavřen v delší dráze.  se tímto efektem směrem do hloubky vodiče rychle zmenšuje a tím zaniká i proud, který způsobuje. Tento efekt je tím větší (rychlejší směrem dovnitř vodiče) čím lepší vodivost vodič má.

Klasický případ plného vodiče s kruhovým průřezem je jen speciálním případem. Je-li vodič plný, nemohou uvnitř býti zdroje pole. Ty se nacházejí vně vodiče a proud má snahu soustřeďovat se při vnějším povrchu vodiče. Podobně u rezonátoru je zdroj uvnitř (budící smyčka) a proud se soustřeďuje na vnitřním povrchu rezonátoru. Tento efekt má velký vliv na impedanci vodičů. Soustřeďuje-li se proud do tenké vrstvy při povrchu, klesá průřez vodiče a jeho odpor roste. Rovněž pokud je penetrace pole do vodiče menší s rostoucím kmitočtem, nebude v něm tolik magnetického toku jako při nižších kmitočtech a vnitřní (vlastní) indukčnost bude se vzrůstem kmitočtu klesat.

Problém penetrace pole do vodiče budeme studovat pomocí Maxwellových rovnic a Ohmova zákona, který může být brán jako definice vodiče:.

Substitucí do Maxwellovy rovnice dostáváme

.

Provedeme divergenci obou stran:  .

Předpokládáme látku bez polarizačních nábojů, . Použili jsme vztahu a záměnnosti derivací podle času a podle souřadnic.

Pokud jsou derivace podle různých souřadnic záměnné, platí

.

Nyní využijeme Maxwellovy rovnice popisující Gaussovu větu a dostaneme . Což je diferenciální rovnice pro ρ v závislosti na čase. Řešením je:

    , kde .

Časová konstanta τ je velmi malá (ε/σ je časová konstanta, rozměr [ε/σ]= F.m^-1/Ω ^-1m^-1= C V^-1/A V^-1=A.s/A=s). Například pro grafit  je (ε_r ≈ 5, σ =0,12 S/m) τ = 0,37 ns. To znamená, že i kdybychom dovnitř vodiče nějaký náboj umístili, ""odteče"" rychle k povrchu a v ustáleném stavu bude ρ = 0.

Tento závěr lze dokázat i následujícím způsobem:

Předpokládáme harmonicky se měnící s časem. Z Maxwellovy rovnice dostaneme . Provedeme-li divergenci, dostáváme  . Tento výsledek je třeba komentovat v tom smyslu, že se jedná o makroskopickou teorii a tedy objem použitý v definici divergence, nesmí být příliš malý, abychom do něj neuzavřeli právě jen jeden elektron (viz [3] str. 15). Představa je tato: v pevné látce se elektrony pohybují mezi kladnými ionty v mříži, střední výsledný náboj přes rozumně veliký objem je vždy nulový. I když by byl brán objem v určitém místě vodiče, tak náboj stále stejných iontů by byl kompenzován různými elektrony, které se pohybují a tvoří tak proud. Tento výsledek vyšel z Maxwellových rovnic prostou aplikací . Pokud toto platí, jsou správné i naše další úvahy. Například ve vakuu platí: proud diody v oblasti, kdy je kontrolován prostorovým nábojem, je úměrný V^3/2 a tedy neplatí . Nelze definovat ε, σ  nezávislé na .

Všimněme si nyní členu, kde se vyskytuje posuvný proud: . Členy, které porovnáváme, jsou σ a ωε. K porovnání potřebujeme znát relativní permitivitu vodičů. Ta je těžko zjistitelná, ale dá se předpokládat, že ε_r u vodičů bude ve stejném rozsahu jako u nevodičů. Např. pro Platinu je ε_r=10, pak je člen ωε roven σ při frekvenci 1,5x10¹⁵ Hz. To odpovídá kmitočtu ultrafialového světla. Důsledkem je, že pro všechny vodiče kromě těch nejhorších (např. Země) je posuvný proud naprosto zanedbatelný vzhledem k vodivostním proudům pro libovolné kmitočty užívané pro radiovou komunikaci (družicové komunikace jsou v řádu 10 GHz = 10¹⁰ Hz).

Pro dobrý vodič platí:

1. hustota volného náboje uvnitř vodiče je nulová, ρ = 0

2. 

3. posuvný proud

Dříve než spočítáme vlastní skin efekt, odvodíme rovnice popisující pole a proud ve vodiči. Vyjdeme z rotačních rovnic a budeme předpokládat zanedbatelný posuvný proud   .

Proveďme rotaci obou stran: .

Dosadíme z Maxwellových rovnic

a dostaneme

.

To je diferenciální rovnice velmi podobná vlnové rovnici. Někdy se jí říká rovnice skin efektu. Vzhledem k tomu, že jsme výše odvodili, že na vodiči je , lze obdobný vztah napsat pro:

Vynásobíme-li rovnici σ, můžeme psát totéž pro :

.

Pokud uvažujeme harmonické změny a ustálený stav, přejdou tyto tři rovnice na

         .

To jsou vztahy mezi časovými a prostorovými derivacemi v libovolném bodě vodiče.

Nyní je vyřešíme pro určité speciální okrajové podmínky dané tvarem vodiče.

Případ rovinného vodiče nekonečné tloušťky ( vodič vyplňuje poloprostor x < o).

Tento případ se může zdát nepříliš vhodný pro praxi. Nicméně uvidíme, že hloubka, do které je pole (i proud) koncentrováno pod povrchem vodiče je velmi malá, takže v podstatě libovolná tloušťka materiálu bude „dostatečně nekonečná“ při radiových frekvencích. Rovněž bude-li mít vodič zakřivený povrch, bude rádius tohoto zakřivení mnohem větší nežli hloubka povrchu. Tedy i zakřivený vodič v tomto měřítku bude možné brát „téměř “ jako rovinný.

Mějme tedy povrch vodiče v rovině y - z. Počítáme změnu (nebo , nebo ) se souřadnicí x. Pro zjednodušení pootočíme soustavu souřadnic tak, že osa z je ve směru proudu, tedy =(0,0,i_z). Dosadíme-li nyní do našich rovnic, dostaneme:

Vezmeme-li odmocninu s kladným znaménkem, bude , kde . Lze si ověřit, že [δ] =[m].

Řešení hledáme ve tvaru . Proud nemůže s x vzrůstat do ∞, a tak C₂ = 0. Pokud dále předpokládáme, že na povrchu vodiče je i_z = i_o, dostáváme řešení i_z = i_o e^-τx.

Pokud použijeme δ dostaneme: .

Je vidět, že proud jednak ubývá v amplitudě jako , jednak točí fázi tak, že 360^o stočení fáze odpovídá , neboli při hloubce má proud opačný směr než na povrchu vodiče a při hloubce má opět stejný směr jako na povrchu vodiče.

Z našeho jednoduchého výpočtu plyne několik důležitých závěrů:

1. Hloubka skinu δ je tím menší, čím je vyšší kmitočet, vodivost, případně permeabilita materiálu, neboť δ je nepřímo úměrné odmocnině jejich součinu. 

2. Spočítáme-li δ, neznamená to, že proud (pole) neproniká hlouběji. Je třeba vzít v úvahu exponenciální závislost.

3. Výsledek platí přesně jen pro rovinný, nekonečný vodič. Pokud má vodič křivost charakterizovanou poloměrem r , pak abychom mohli tyto výrazy použít, musí platit . Je-li , dochází k odchylce.

4. Parametr δ představuje pro určitý vodič materiálovou konstantu a využívá se při mnoha výpočtech (některé z nich jsou uvedeny dále).

Již dříve jsme v podstatě formálně zavedli pojem vnitřní impedance. Spočítáme ji v případě rovinného vodiče. Vzhledem k tomu, že vnitřní impedance je definována s použitím celkového proudu a ne hustoty proudu, musíme vytknout ve vodiči kvádr o nekonečné délce a podstavě 1x1 cm (1x1m pro zaryté uživatele SI soustavy) a proud ve směru z (opět máme vhodně volenu soustavu souřadnic s osou z ve směru proudu) počítáme pro jednotkovou „šířku“ ve směru y jako integrál přes x:

.

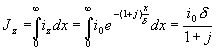Na povrchu vodiče platí Ohmův zákon : .

Vnitřní impedance je definována jako poměr . To je komplexní číslo, a proto lze napsat . Nerozlišujeme žádnými symboly komplexní hodnoty od reálných. V případě potíží je možné na reálné hodnoty pohlížet jako na komplexní s nulovou fází.

      ,      

Odpor a vnitřní indukčnost rovinného vodiče jsou si rovny nezávisle na kmitočtu a fáze Z_s je 45^o. Hloubku skinu  je taková hloubka (tloušťka), při které je stejnosměrný odpor rovinného vodiče tloušťky δ stejný jako povrchový odpor rovinného, nekonečně silného vodiče. R_s se nazývá povrchový odpor. Spočítali jsme jej pro jednotku délky ve směru z a jednotku šířky ve směru y - viz výše. Pro libovolnou délku x je jej třeba touto délkou násobit a pro libovolnou šířku je jej potřeba touto šířkou dělit (podobně jako paralelně zapojené odpory). Z toho plyne, že R_s je odpor nejen čtverce o jednotkových stranách, ale čtverce o libovolných stranách.R_s se měří v Ω/čtverec, nebo Ω/ (to není vtip, tato značka se skutečně používá). Podobně jako δ může být i R_s materiálovou konstantou (pro určitý kmitočet f).

To, že pole (proud) proniká i dovnitř vodiče a odvozený odpor má reálnou složku, implikuje, že ve vodiči dochází ke ztrátě výkonu (vodič se ohřívá a vlny se odrážejí s menší amplitudou). Střední výkon za jednu periodu na jednotku plochy rovinného vodiče najdeme s pomocí R_s jako .

1/2 vyjde z integrace kvadrátu harmonické veličiny . [w]= W/m².

Zde jsme použili interpretaci povrchového odporu pomocí hloubky skinu, jako kdyby proudová hustota byla v tloušťce δ konstantní a hlouběji pak nulová. Přesně by se tento vzorec dal odvodit pomocí známé závislosti proudové hustoty na tloušťce a integrací přes tloušťku od 0 do ∞.

Zkusme dát tento výraz do souvislosti s magnetickým polem na povrchu vodiče. Předpokládáme stále, že proud teče ve směru z a souřadnice x udává hloubku pod povrchem. Proud J_z představuje povrchový proud na jednotku délky (šířky, souřadnice ve směru y), má tedy rozměr Am^-1.  

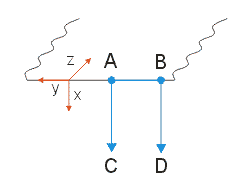Provedeme nyní úvahu podobnou jako v případu výpočtu změn tangenciálních a normálových složek polí na rozhraní dvou látek. Integrujeme intenzitu magnetického pole přes křivku ABCD, kde body C a D jsou nekonečně hluboko pod povrchem vodiče (x →∞). Magnetické pole bude mít jen y - ovou složku, = (0,Hy ,0) a příspěvky po dráze AC a BD budou nulové. Příspěvek po dráze CD velmi hluboko pod povrchem vodiče bude také roven nule, protože tam Hy = 0. Platí:       , kde značí hodnotu složky Hy na povrchu vodiče.

Obr. 1.10.2 Ilustrace k úvaze

Tento křivkový integrál se musí podle Ampérova zákona rovnat proudu obepnutému touto křivkou. Vzhledem k tomu, že zanedbáváme posuvný proud, zůstane jen proud vodivostní: , kde je vzdálenost bodů A,B. Znaménko minus udává směr H_y - opačný než je kladný směr osy y, pokud J_z teče v kladném směru osy z. Platí neboli J_z = - H_tg.

Vztah pro plošnou hustotu výkonu je roven  . Tento výraz, který lze získat z odvození při použití Poyntingova vektoru (viz [2] str. 37-39, vztah (1.31)).

Bude vhodné spočítat si R_s a L_i pro případ vodiče kruhového průřezu.

Nejprve vezmeme případ velmi vysokých kmitočtů: δ je malé a povrch vodiče je možné brát jako rovinný se šířkou rovnou obvodu vodiče. Poloměr vodiče r_o >> d. 

Člen jsme odvodili výše.

a  představuje „šířku“, kterou musíme odpor dělit - jako by bylo odporů o velikosti spojeno paralelně.

Tedy .

Pro stejnosměrné obvody a obvody s nízkými kmitočty je proud prakticky rovnoměrně rozložen přes průřez vodiče. Odpor na jednotku délky spočítáme jako .

Lze ukázat, že pro frekvence, pro které je hloubka skinu (asi do r_o≈δ) je možno použít vzorec .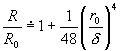

Indukčnost L_i vypočítáme na základě energetických úvah. Již dříve jsme odvodili, že hustota energie magnetického pole je dána vztahem

 .

 Předpokládáme-li kmitočty tak nízké, že rozložení proudu přes průřez vodiče je rovnoměrné, platí pro r < r_o . Lze odvodit z Ampérova zákona.

Počítáme v cylindrických souřadnicích.

Spočítáme indukčnost na jednotku délky:

= .

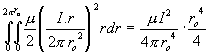Upravíme na tvar .

Lze ukázat, že indukčnost odvozená za předpokladu nízkých kmitočtů klesá s rostoucí frekvencí. Pro velmi vysoké kmitočty jsme ukázali, že ωL_i je konstantní a rovné R_s . L_i klesá nepřímo úměrně s kmitočtem. Induktivní odpor X_L = ωL_i v závislosti na kmitočtu roste z nuly až na hodnotu danou . Pro ω = 0 je sice , ale ω = 0.

Nyní již jsme položili základy k tomu, abychom se mohli zabývat přenosovým vedením. Jako nejjednodušší příklad vyřešíme homogenní vedení, tj. vedení, které má stále stejné parametry na jednotku délky - odpor, svod, kapacitu a indukčnost. Řešení budeme provádět pomocí rozdělení linky na úseky infinitezimální délky a aplikací Kirchhoffových zákonů.

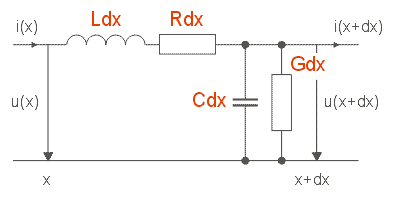
Obr. 1.10.3 Infinitezimální úsek homogenního vedení

Označme L,R,C,G příslušné veličiny na jednotku délky vedení - rozměry příslušných veličin obsahují m^-1.

Z Kirchhoffových zákonů dostaneme:

Vyjádříme-li nyní 

dostaneme z uvedených rovnic:

V případě bezeztrátového vedení tj. R = G = 0, můžeme tyto rovnice upravit na tvar obdobný vlnové rovnici:

Řešením těchto rovnic je obecně každá (diferencovatelná) funkce argumentu , neboť je-li například , je

.

Funkce takového argumentu reprezentuje vlnu šířící se po vedení rychlostí v.

Zatím jsme nepředpokládali, že vedení je buzeno sinusovým signálem. Funkce F může být např. známá „skoková“ funkce, která z původní 0 nabude pro x = 0 a t = 0 hodnotu 1 - zapneme spínač.

Pokud bychom osciloskopem měřili průběhy napětí ve dvou místech vzdálených od sebe o  x_o, zjistili bychom, že čas potřebný k průchodu této vzdálenost je úměrný x_o, t = x_o/ v. Amplituda zůstává díky bezeztrátovosti stejná jako na začátku veden.

Uvažujme nyní vedení ztrátové, tj. R ≠ 0 a G ≠ 0, ale pro zjednodušení harmonicky buzené:

.

Pak časové derivace přejdou na násobení a máme:

.

Jedná se o svázané diferenciální rovnice (soustavu rovnic), které by se musely řešit vždy další derivací jedné z nich a dosazením do druhé rovnice. Tímto postupem dostaneme lineární diferenciální rovnice 2.řádu v proměnné x, které se řeší substitucí .

Tím bychom dostali řešení typu:

,

přičemž

,

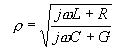γ je konstanta šíření, která, je-li ryze imaginární, reprezentuje vlnový vektor a její eventuelní reálná část představuje útlum amplitudy na jednotku délky. Parametry A a B jsou závislé na délce vedení a na impedanci, kterou je vedení na konci zakončeno.

Pro příklad vedení délky l, zakončeného impedancí Z platí

U(x = 0) = U_o , U(x = l) = Z.I(l) 

a dostáváme

 A = U_o,

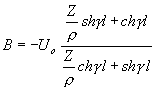
a výrazy pro U(x) a I(x) se dají upravit následovně:

.

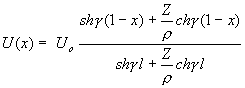
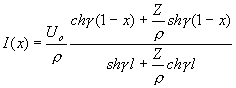Někdy se ρ píše ve tvaru , kde Z = jωL + R  je podélná impedance, Y = jωC + G je příčná admitance a pro γ platí: . Rozepíšeme-li γ jako α + jβ, vyplyne závislost α i β  na frekvenci ω. V limitě ω → ∞ se α →  a β → 0. Z tohoto důvodu se často i pro vedení slabě ztrátová počítá charakteristická impedance jako , neboť pro běžné vedení je fázový úhel ρ i pro malé frekvence velmi malý.

Na druhé straně rozepíšeme-li konstantu šíření jako α + jβ, dostaneme i pro velmi nízké kmitočty nenulovou reálnou složku, která se pro ω→∞ rovněž blíží určité limitní hodnotě, imaginární složka se blíží . Tato limitní hodnota není jen funkcí R a G, ale i funkcí C a L. Dá se tedy očekávat, že pro minimalizaci β pro nejmenší útlum, bude třeba sladit R s ostatními parametry vedení. To může mít důsledky pro jejich rozměry. Spočítáme pro γ = α + jβ reálnou i imaginární složku. Máme

 

a odtud dostaneme dvě rovnice pro reálnou složku:

.

Eliminujeme-li β, dostaneme

 ,

což je bikvadratická rovnice řešitelná substitucí α²=x.

Fyzikální smysl (α>0) má řešení:

.

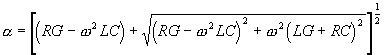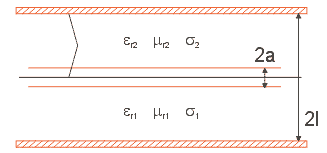
V případě malých ztrát, tj. R << ωL a G << ωC neboli RG << ω²LC, lze tento vztah upravit vytknutím z hranaté závorky. Použitím nerovnosti a pro dostatečně velké ω odmocninu rozvineme se zanedbáním členů vyššího řádu na

.

A to je hledaný vztah.

	Pro koaxiální vedení je možné odvodit tyto vztahy:
Obr. 1.10.4 Infinitezimální úsek koaxiálního vedení

 

Otázka zní: Závisí α na ξ = b/a? A závisí-li, nemá pro nějaké ξ minimum?

Když spočítáme člen , vidíme, že na ξ nezávisí. Člen lze naopak napsat jako konstanta: . Extrém nastává je-li derivace rovna nule nebo-li konstanta . Po vyřešení například pomocí počítače dostaneme ξ ≈ 3,6. Několika dosazeními a výpočtem druhé derivace je možné se přesvědčit, že jde skutečně o minimum. Toto minimum je ploché, pro ξ = 2,3 až 6 vzroste maximálně o 10 %. Po dosazení charakteristická impedance ρ ≈ 70,2 Ω. Odtud plyne známá impedance koaxiálních kabelů v rozmezí 50 až 75 Ω. Útlum takovéhoto koaxiálního vedení je v mezích možností minimální.

Lze se setkat se zakončením vedení charakteristickou impedancí, zkratem nebo nekonečným odporem. Zabývejme se jejich interpretací a výpočtem činitele odrazu. Činitel odrazu je z hlediska veličinou, kterou nelze přímo měřit. Proto se často nahrazuje veličinou související, činitelem stojatého vlnění. Je zřejmé, že poběží-li po vedení vlna a částečně se na konci odrazí, vznikne stojaté vlnění, které bude charakterizováno vzdáleností uzlů a amplitudou napětí v maximech a minimech. Poměr 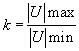nazýváme činitelem stojatého vlnění.

Použijeme-li jako indikátoru mikrovlnnou diodu a upravíme měření tak, abychom snímáním napětí neporušili poměry na vedení, můžeme změřit jak |U|_max, tak |U|_min a vypočítat tak k. Zbývá odvodit, jaký vztah má činitel stojatého vlnění ke koeficientu odrazu. Tento vztah odvodíme následující jednoduchou úvahou:

Postupuje-li po vedení vlna napětí s amplitudou |U|, pak po odrazu bude mít amplitudu r·|U| a opačný směr. Podle toho, v jaké fázi se vlna odráží, dříve či později doje k tomu, že vlna odražená a dopadající budou mít stejnou fázi. Jejich amplitudy se sečtou. To bude maximální napětí na stojaté vlně

   ;    kde r může být obecně komplexní.

Proto musíme brát jen jeho amplitudu.

Obdobně nastane dříve či později (dále či blíže) situace, kdy dopadající a odražená vlna jsou v protifázi. Nastane minimum stojatého vlnění, kde

.

Pro k pak dostáváme 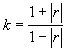. A to už je reálné číslo, které se dostane přímo z měření.

Z toho plyne jeden důležitý výsledek, zejména pro dlouhá přenosová vedení. Tam, kde si neuvědomujeme, kde je vedení zakončeno nebo to ani přesně nevíme. Stojaté vlnění na přenosovém vedení sítě může způsobit, že měříme-li voltmetrem hodnoty napětí v různých místech vedení, naměříme různé hodnoty, které nebudou monotónně ubývat směrem od generátoru ke spotřebiči, tak jak jsme zvyklí ze stejnosměrných obvodů. Naopak, často může nastat případ, že na spotřebiči je vyšší napětí, než naměříme několik desítek kilometrů před spotřebičem směrem ke zdroji. Tento efekt byl nazván Ferrantiho jevem a je vysvětlitelný, uvažujeme-li konečnou vlnovou délku. Při kmitočtech 50 Hz je to asi 3000 km. Vzdálenost maxim nebo minim je λ/2. Tedy vzdálenost maxima od minima je 750 km. Odtud vyplývá, že efekt může být pozorovatelný na vzdálenosti řádově stovek kilometrů od spotřebiče.

Úloha:

Provozní parametry sdělovacího vedení délky l = 300 km jsou Z_o = 613 e^-j·6,67 Ω, γ = 1,775·10^-2 e^j.79,33 km^-1. Vedení je na konci zatíženo spotřebičem s impedancí Z_e = 2800 e^j.38 Ω a komplexní amplituda napětí na konci vedení je U_k = 1,0 e^j.47 V.

Spočítejte průběh absolutní hodnoty napětí podél vedení.

Výsledek: Ferrantiho jev nastává ve vzdálenosti cca 50 až 148 km od konce vedení  - od spotřebiče.

Pro přizpůsobení vedení je často třeba znát impedanci vedení v určitém místě, známe-li jeho parametry a zatěžovací impedanci, a nebo naopak určit zatěžovací impedanci z měření na vedení. Pro tyto účely byl vyvinut kruhový diagram -  Smithův diagram. Základem pro tento diagram je vztah pro impedanci vedení v závislosti na charakteristické a zatěžovací impedanci, konstantě šíření a vzdálenosti od zátěže. Tento vztah je odvozen v dodatku, vztah (D9). Výraz pak nahradíme s použitím reálné a imaginární části konstanty šíření γ: .

Výraz pro impedanci vedení se dá přepsat do tvaru .

Zavedeme další proměnnou - fázi - vztahem .

Z_o lze napsat jako .

 Užitím vztahu dostaneme: .

Účelem kruhového diagramu je zjednodušení vzájemného vztahu mezi Z_o = R_o + jx_o a fází , tj. nalezení u a v za předpokladu, že je dáno R_o, x_o anebo opačně nalézt R_o, x_o za předpokladu, že jsou dány  u, v. 

Zavedeme-li , bude pak .

Pro vzájemné vztahy mezi  p, q, u, v, dostaneme

.

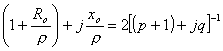To jsou vztahy spojující tyto veličiny v komplexní rovině.

Zavedeme dále veličinu , která má vztah relativní délky vedení vzhledem k vlnové délce.

Polární tvar kruhového diagramu se skládá ze dvou párů souborů křivek v t-rovině:

(1) pár u = konst., n = konst.

(2) pár  a .

Z uvedených rovnic lze odvodit:

a tedy

.

Křivky u = konst. představují kružnice o poloměru e^-2u se středy v počátku. Křivky n = konst. tvoří soubor přímek vycházejících z  počátku se směrnicí -4πn.

Ze vztahu zahrnujícího  a dostaneme po úpravách:

.

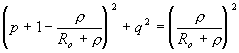
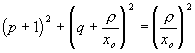Křivky jsou tedy kružnice s poloměry 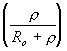se středy v bodech 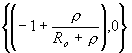. Jakákoliv kružnice protíná osu p (tj.q = 0) v bodech p = -1 a . Všechny kružnice tedy procházejí bodem (-1,0) v rovině t.

Křivky jsou rovněž kružnice s poloměrem se středy v bodech , které procházejí bodem (-1,0). V tomto bodě je osa p (q = 0) tečnou ke všem těmto kružnicím.

Dá se ukázat, že křivky (kružnice) a tvoří ortogonální systém. Další interpretace plyne ze zavedení t jako -r tj. .První pár souborů křivek se dá snadno konstruovat pravítkem a kružítkem, druhý pár souborů křivek se tiskne ve tvaru diagramu zvaného Smithův diagram, který má po obvodu stupnici - viz obr.1.10.5.

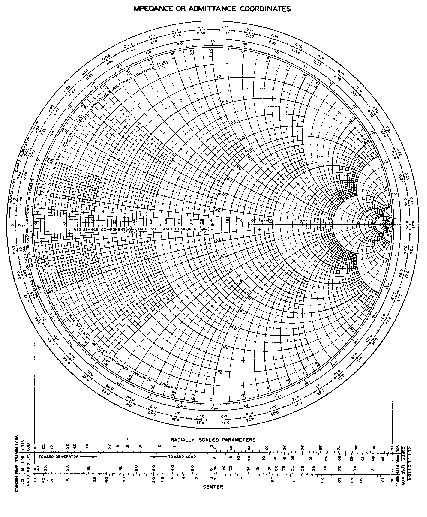
Obr. 1.10.5 Smithův diagram - detail

Na pravítku je výhodné vyznačit místo koeficientu r, který se nedá měřit, koeficient stojatého vlnění , který se měří pomocí měřícího vedení (slotted line).

Na obrázcích v podkapitole Řešené příklady je uvedeno několik způsobů použití Smithova diagramu. Je ovšem třeba říci, že stejných výsledků, ale s větší přesností, lze dosáhnout výpočtem na počítači přímo z původních výrazů. Tím se však ochuzujeme o názornost. Zejména v tom smyslu, že z diagramu je zřejmá přesnost výsledků.

<<< předchozí | hlavní stránka | další >>>