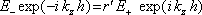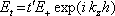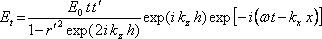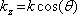2.2 Mnohosvazková interference
Nyní se budeme zabývat případem, kdy dopadá rovinná monochromatická vlna na planparalelní desku (například skleněnou), jejíž plochy jsou pokryty tenkými vrstvami s velkou odrazivostí. V takovém případě se vlny na horní i dolní ploše částečně odráží a částečně procházejí a vzhledem k tomu, že je odrazivost velká, je nutné při interferenci uvažovat velký počet vln. Situace je schematicky znázorněna na obr. 5.13. Rovinná monochromatická vlna dopadá pod úhlem
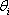 , její amplituda je
, její amplituda je
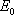 . Pro jednoduchost budeme uvažovat reálnou skalární amplitudu. Na obrázku jsou znázorněny jednotlivé paprsky, které vznikají různým počtem průchodů a odrazů. Kromě různých velikostí amplitud, které jsou důsledkem násobení původní amplitudy relevantními koeficienty propustnosti a odrazivosti, mají vlny také různé fáze. Fázový rozdíl
. Pro jednoduchost budeme uvažovat reálnou skalární amplitudu. Na obrázku jsou znázorněny jednotlivé paprsky, které vznikají různým počtem průchodů a odrazů. Kromě různých velikostí amplitud, které jsou důsledkem násobení původní amplitudy relevantními koeficienty propustnosti a odrazivosti, mají vlny také různé fáze. Fázový rozdíl
 mezi paprskem dvěma následujícími paprsky jsme vypočítali již dříve, je dán vztahem (5.31). Při dopadu světla na plochu desky z okolního prostředí (vzduchu například) do skleněné desky jsou amplitudové koeficienty odrazu
mezi paprskem dvěma následujícími paprsky jsme vypočítali již dříve, je dán vztahem (5.31). Při dopadu světla na plochu desky z okolního prostředí (vzduchu například) do skleněné desky jsou amplitudové koeficienty odrazu
 a propustnosti
a propustnosti
 , při
, při
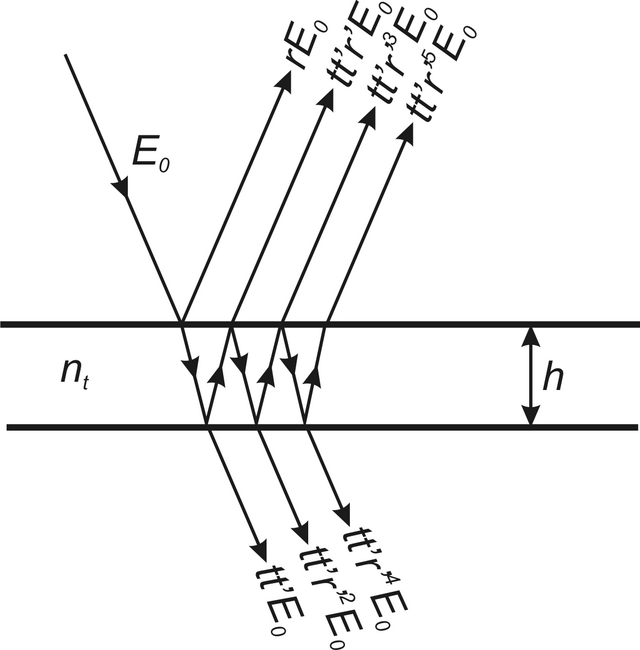 Obr. 5.13
Obr. 5.13 Mnohosvazková interference na planparalelní vrstvě. U jednotlivých paprsků jsou uvedeny jejich amplitudy
dopadu z desky do vzduchu
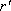 a
a
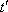 . Pomocí Fresnelových vzorců lze ukázat platnost tzv. Stokesových vztahů
. Pomocí Fresnelových vzorců lze ukázat platnost tzv. Stokesových vztahů
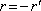 |
(5.40) |
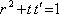 |
(5.41) |
Vypočítáme nyní výsledné pole, které projde deskou. Dopadající vlnu bereme reálnou, paprsek 1 prošlý deskou bez odrazu má fázový posuv vůči dopadající vlně daný náběhem fáze při jednom průchodu deskou
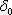 . Jednotlivé svazky mají komplexní amplitudy
. Jednotlivé svazky mají komplexní amplitudy

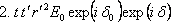
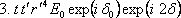 |
(5.42) |
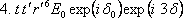 .......
Celkové pole prošlé deskou je tedy rovno součtu dílčích vln,
.......
Celkové pole prošlé deskou je tedy rovno součtu dílčích vln,
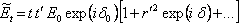 |
(5.43) |
V hranaté závorce je součet geometrické řady s kvocientem
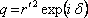 |
(5.44) |
Součet řady je
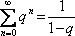 (pro
(pro
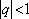 , což je jistě v našem případě splněno).
Komplexní amplituda prošlého pole je tedy
, což je jistě v našem případě splněno).
Komplexní amplituda prošlého pole je tedy
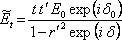 |
(5.45) |
Důležitá je intenzita světla, která podle vztahu (5.5) je
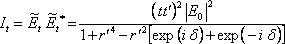 |
(5.46) |
Po úpravách a využitím Stokesových vztahů (5.40, 5.41) máme
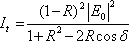 |
(5.47) |
neboli
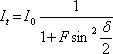 |
(5.48) |
Zde
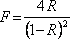 |
(5.49) |
je parametr nazývaný jemností (
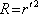 je intenzitní odrazivost na rozhraní). Závisí silně na odrazivosti R, jejímž krajním hodnotám 0 a 1 odpovídají pro F krajní hodnoty 0 a nekonečno.
Propustnost desky je možné zavést jako
je intenzitní odrazivost na rozhraní). Závisí silně na odrazivosti R, jejímž krajním hodnotám 0 a 1 odpovídají pro F krajní hodnoty 0 a nekonečno.
Propustnost desky je možné zavést jako
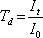 |
(5.50) |
zde jako výše je
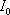 intenzita dopadajícího světla. Pokud uvažujeme desku bez absorpce, musí pro intenzitu odraženou od desky platit
intenzita dopadajícího světla. Pokud uvažujeme desku bez absorpce, musí pro intenzitu odraženou od desky platit
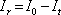 |
(5.51) |
Zavedeme-li odrazivost desky jako
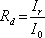 |
(5.52) |
musí zřejmě být
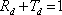 |
(5.53) |
Propustnost, resp. odrazivost desky vypočítaná podle rov. (5-48), (5.50), (5.51) a (5.52) je jako funkce δ znázorněna na obr. 5.14 (Airyho funkce). Je zřejmé, že tvar Airyho funkce závisí na parametru F, který charakterizuje kontrast funkce. Skutečně, podle vztahu (5.48) je maximum propustnosti Td rovno 1 a minimum 1/(1+F). Kontrast můžeme charakterizovat výrazem
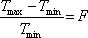 |
(5.54) |
Z uvedeného vztahu pro propustnost je zřejmé, že maximální hodnota propustnosti je rovna jedné. Tento případ nastane vždy, když sin ve jmenovateli vymizí, tedy pro
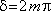 |
(5.55) |
V tomto případě je tedy
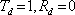 |
(5.56) |
Přitom se ovšem samozřejmě odráží první svazek. Nulová hodnota celkové odrazivosti tedy znamená, že intenzita prvního odraženého svazku musí být stejně velká jako celkový příspěvek do "odraženého" světla (pole s opačnou fází) pocházející od všech dalších paprsků. Jak plyne z Fresnelových vzorců, fáze vlny se při průchodu rozhraním nemění. Proto je první odražený paprsek v protifázi k ostatním paprskům, protože platí
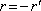 .
Speciálním, ale častým případem je kolmý dopad vlny na desku. Pak podle (5.31) je
.
Speciálním, ale častým případem je kolmý dopad vlny na desku. Pak podle (5.31) je
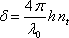 |
(5.57) |
a podmínka maximální propustnosti (5.32) (předpokládáme zde
 ) odpovídá výrazu spojujícímu optickou tloušťku desky s vlnovou délkou světla ve vakuu
) odpovídá výrazu spojujícímu optickou tloušťku desky s vlnovou délkou světla ve vakuu
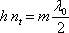 |
(5.58) |
tedy řečeno slovy, tloušťka desky musí být rovna celistvému násobku polovln. Číslo m , které udává počet polovln na tloušťce desky se nazývá řádem interference.
Stejně lze vyšetřovat mnohosvazkovou interferenci, která vzniká při odrazech mezi dvěma rovnoběžnými zrcadly, mezi nimiž je vzduchová mezera. Takové uspořádání se užívá v interferometrii a nazývá se Fabryho - Perotův interferometr. Podrobně budeme jeho vlastnosti rozebírat v kapitole o intreferometrech.
2.2.1 Mnohosvazková nebo dvousvazková interference na planparalelní desce
Interferenci světla na planparalelní desce jsme rozebírali již dříve jako dvousvazkovou interferenci. Kdy se tedy můžeme omezit pouze na první dva paprsky (odrazy)? Jako kritérium můžeme vzít velikost podílu amplitud druhého a prvního paprsku - pokud se bude blížit jedné, v případě splnění odpovídající fázové podmínky se dva paprsky téměř vyruší a další není nutné uvažovat. Zmíněný podíl amplitud je roven
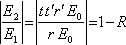 |
(5.59) |
Například pro kolmý dopad na skleněnou destičku (
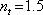 ) je
) je
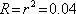 a zmíněný podíl je roven 0.96, což znamená, že se dva odražené paprsky vyruší až na 4 %.
a zmíněný podíl je roven 0.96, což znamená, že se dva odražené paprsky vyruší až na 4 %.
Stejně lze vyšetřovat mnohosvazkovou interferenci, která vzniká při odrazech mezi dvěma rovnoběžnými zrcadly, mezi nimiž je vzduchová mezera. Takové uspořádání se užívá v interferometrii a nazývá se Fabryho - Perotův interferometr. Podrobně budeme jeho vlastnosti rozebírat v kapitole o intreferometrech.
2.2.2 Jiné odvození Airyho funkce
Jakkoliv je uvedené odvození názorné, můžeme Airyho funkci odvodit i jednoduchou úvahou založenou na poměrech amplitud při odrazu a průchodu. Ukážeme to na Fabryho - Perotově interferometru, který je tvořen dvěma planparalelními zrcadly. Geometrie je podobná jako u desky, pro zrcadla ovšem
 , prostor mezi zrcadly je vyplněn vzduchem, tj.
, prostor mezi zrcadly je vyplněn vzduchem, tj.
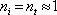 . Amplitudové propustnosti a odrazivosti opět označíme t a r "zvenku" , resp. t' a r' "zevnitř". Budeme uvažovat postup vln v rovině obrázku, zvolíme souřadný systém tak, že osa z bude mít směr normály k povrchu desky, osa x bude ležet v rovině obrázku - viz obr. 5.15. Pole mezi povrchy desky je složeno z vlny postupující v kladném smyslu osy z (ve směru dopadající vlny)
. Amplitudové propustnosti a odrazivosti opět označíme t a r "zvenku" , resp. t' a r' "zevnitř". Budeme uvažovat postup vln v rovině obrázku, zvolíme souřadný systém tak, že osa z bude mít směr normály k povrchu desky, osa x bude ležet v rovině obrázku - viz obr. 5.15. Pole mezi povrchy desky je složeno z vlny postupující v kladném smyslu osy z (ve směru dopadající vlny)
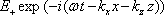 |
(5.60) |
a vlny postupující v opačném směru (po odrazu - mění se pouze znaménko u členu se souřadnicí z)
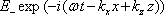 |
(5.61) |
Zvenku na zrcadlo dopadá vlna
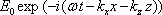 |
(5.62) |
prošlá vlna za výstupním zrcadlem je
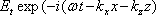 |
(5.63) |
Pomineme-li na chvíli časovou a x-ovou závislost, která je pro všechny vlny stejná, můžeme jednoduše sestavit rovnice vyjadřující propustnost a odrazivost na obou zrcadlech. Na prvním zrcadle (z=0)
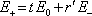 |
(5.64) |
Na druhém zrcadle (
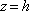 )
)
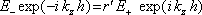 |
(5.65) |
a procházející pole
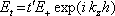 |
(5.66) |
Protože chceme najít vztah mezi polem dopadajícím a propuštěným, vyjádříme E+ pomocí E0 z (5.64) a (5.65) a dosadíme do (5.66). Dostaneme (po vynásobení faktorem obsahujícím časovou a x-ovou závislost)
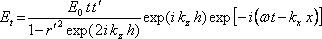 |
(5.67) |
což souhlasí se vztahem (5.45), který jsme odvodili výše, vzhledem k tomu, že
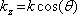 |
(5.68) |
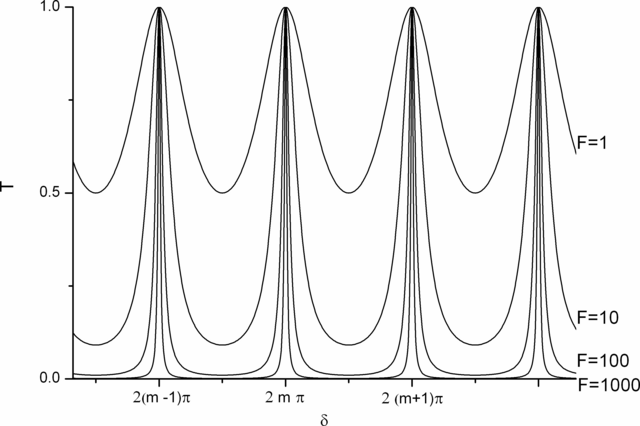 Obr. 5.14a
Obr. 5.14a Propustnost
T
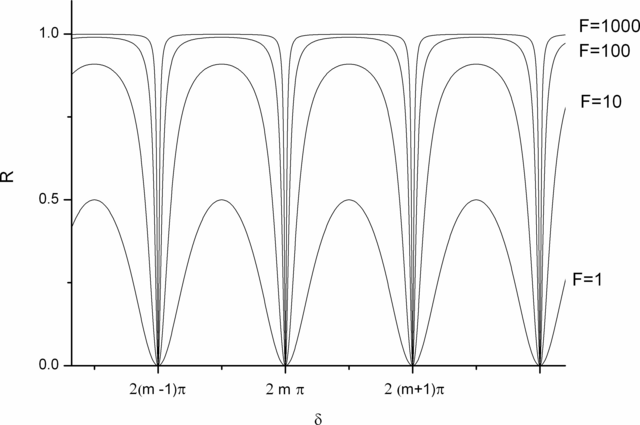 Obr. 5.14b
Obr. 5.14b odrazivost
R planparalelní desky při mnohosvazkové interferenci jako funkce fázového zpoždění
δ (Airyho funkce).
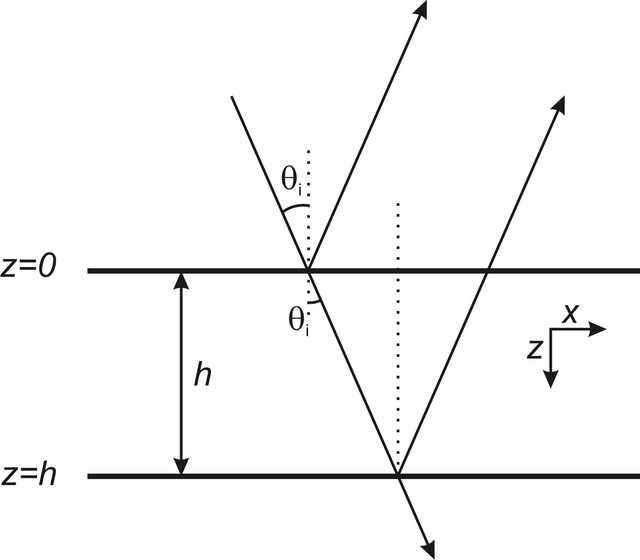 Obr. 5.15
Obr. 5.15 Mnohosvazková interference na dvou planparalelních zrcadlech, alternativní odvození Airyho funkce
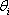 , její amplituda je
, její amplituda je
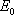 . Pro jednoduchost budeme uvažovat reálnou skalární amplitudu. Na obrázku jsou znázorněny jednotlivé paprsky, které vznikají různým počtem průchodů a odrazů. Kromě různých velikostí amplitud, které jsou důsledkem násobení původní amplitudy relevantními koeficienty propustnosti a odrazivosti, mají vlny také různé fáze. Fázový rozdíl
. Pro jednoduchost budeme uvažovat reálnou skalární amplitudu. Na obrázku jsou znázorněny jednotlivé paprsky, které vznikají různým počtem průchodů a odrazů. Kromě různých velikostí amplitud, které jsou důsledkem násobení původní amplitudy relevantními koeficienty propustnosti a odrazivosti, mají vlny také různé fáze. Fázový rozdíl
 mezi paprskem dvěma následujícími paprsky jsme vypočítali již dříve, je dán vztahem (5.31). Při dopadu světla na plochu desky z okolního prostředí (vzduchu například) do skleněné desky jsou amplitudové koeficienty odrazu
mezi paprskem dvěma následujícími paprsky jsme vypočítali již dříve, je dán vztahem (5.31). Při dopadu světla na plochu desky z okolního prostředí (vzduchu například) do skleněné desky jsou amplitudové koeficienty odrazu
 a propustnosti
a propustnosti
 , při
, při

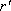 a
a
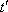 . Pomocí Fresnelových vzorců lze ukázat platnost tzv. Stokesových vztahů
. Pomocí Fresnelových vzorců lze ukázat platnost tzv. Stokesových vztahů
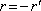
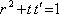
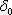 . Jednotlivé svazky mají komplexní amplitudy
. Jednotlivé svazky mají komplexní amplitudy

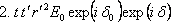
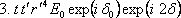
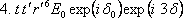 .......
Celkové pole prošlé deskou je tedy rovno součtu dílčích vln,
.......
Celkové pole prošlé deskou je tedy rovno součtu dílčích vln,
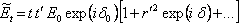
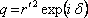
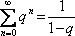 (pro
(pro
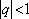 , což je jistě v našem případě splněno).
Komplexní amplituda prošlého pole je tedy
, což je jistě v našem případě splněno).
Komplexní amplituda prošlého pole je tedy
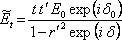
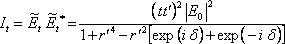
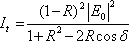
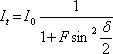
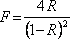
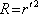 je intenzitní odrazivost na rozhraní). Závisí silně na odrazivosti R, jejímž krajním hodnotám 0 a 1 odpovídají pro F krajní hodnoty 0 a nekonečno.
Propustnost desky je možné zavést jako
je intenzitní odrazivost na rozhraní). Závisí silně na odrazivosti R, jejímž krajním hodnotám 0 a 1 odpovídají pro F krajní hodnoty 0 a nekonečno.
Propustnost desky je možné zavést jako
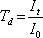
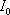 intenzita dopadajícího světla. Pokud uvažujeme desku bez absorpce, musí pro intenzitu odraženou od desky platit
intenzita dopadajícího světla. Pokud uvažujeme desku bez absorpce, musí pro intenzitu odraženou od desky platit
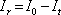
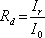
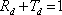
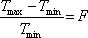
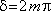
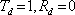
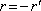 .
Speciálním, ale častým případem je kolmý dopad vlny na desku. Pak podle (5.31) je
.
Speciálním, ale častým případem je kolmý dopad vlny na desku. Pak podle (5.31) je
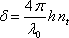
 ) odpovídá výrazu spojujícímu optickou tloušťku desky s vlnovou délkou světla ve vakuu
) odpovídá výrazu spojujícímu optickou tloušťku desky s vlnovou délkou světla ve vakuu
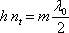
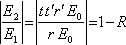
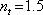 ) je
) je
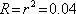 a zmíněný podíl je roven 0.96, což znamená, že se dva odražené paprsky vyruší až na 4 %.
a zmíněný podíl je roven 0.96, což znamená, že se dva odražené paprsky vyruší až na 4 %.
 , prostor mezi zrcadly je vyplněn vzduchem, tj.
, prostor mezi zrcadly je vyplněn vzduchem, tj.
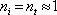 . Amplitudové propustnosti a odrazivosti opět označíme t a r "zvenku" , resp. t' a r' "zevnitř". Budeme uvažovat postup vln v rovině obrázku, zvolíme souřadný systém tak, že osa z bude mít směr normály k povrchu desky, osa x bude ležet v rovině obrázku - viz obr. 5.15. Pole mezi povrchy desky je složeno z vlny postupující v kladném smyslu osy z (ve směru dopadající vlny)
. Amplitudové propustnosti a odrazivosti opět označíme t a r "zvenku" , resp. t' a r' "zevnitř". Budeme uvažovat postup vln v rovině obrázku, zvolíme souřadný systém tak, že osa z bude mít směr normály k povrchu desky, osa x bude ležet v rovině obrázku - viz obr. 5.15. Pole mezi povrchy desky je složeno z vlny postupující v kladném smyslu osy z (ve směru dopadající vlny)
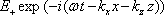
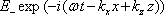
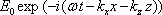
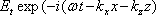
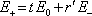
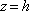 )
)