2.1 Dvojsvazková interference
2.1.1 Interference dvou rovinných světelných vln
Budeme se nyní zabývat interferencí dvou světelných svazků. Pro jednoduchost budeme předpokládat, že interferují dvě rovinné monochromatické vlny se stejnou frekvencí
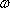 . Popíšeme je pomocí komplexní reprezentace (
. Popíšeme je pomocí komplexní reprezentace (
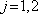 )
)
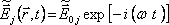 |
(5.2) |
kde jsme do komplexní amplitudy započítali i náběh fáze vlny šířením, tedy
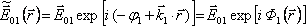 |
(5.3) |
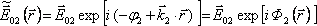 |
(5.4) |
Výsledné pole s komplexní amplitudou
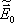 dostaneme podle (5.1). V této kapitole budeme při vyšetřování interferenčních jevů, jak je často zvykem, vyjadřovat intenzitu
dostaneme podle (5.1). V této kapitole budeme při vyšetřování interferenčních jevů, jak je často zvykem, vyjadřovat intenzitu
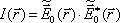 |
(5.5) |
Ve srovnání s výrazem pro intenzitu, který jsme uvedli v 1. kapitole zde pro jednoduchost klademe
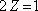 , protože se zabýváme spíše modulací intenzity v prostředí se stejnou impedancí než její skutečnou hodnotou.
, protože se zabýváme spíše modulací intenzity v prostředí se stejnou impedancí než její skutečnou hodnotou.
Přímým dosazením (5.3, 5.4) do (5.1) a (5.5) dostaneme (prostorovou závislost fáze a komplexní amplitudy jsou závislé na
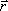 , pro přehlednost argumenty nevypisujeme) pro výslednou intenzitu světla v určitém místě daném polohovým vektorem
, pro přehlednost argumenty nevypisujeme) pro výslednou intenzitu světla v určitém místě daném polohovým vektorem
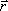
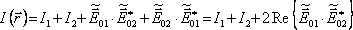 |
(5.6) |
tedy,
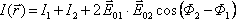 |
(5.7) |
Je zřejmé, že výsledná intenzita dvou světelných polí je dána jejich součtem plus interferenčním členem, jehož velikost závisí na skalárním součinu reálných amplitud obou polí a na kosinu jejich fázového rozdílu v daném místě (obsahuje jak "počáteční fáze vln", tak náběh fáze získaný šířením). Fázový rozdíl mezi dvěma interferujícími vlnami budeme označovat jako
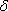 ,
,
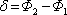 |
(5.8) |
Z rov. (5.6) je zřejmé, že velikost interferenčního členu je úměrná skalárnímu součinu reálných amplitud světelných vln. Pro navzájem kolmo lineárně polarizované vlny je tedy interferenční člen roven nule.
Uvažujme nejprve velmi jednoduchou situaci, kdy interferují dvě vlny, jejichž vlnové vektory leží v rovině y, z , které jsou shodně lineárně polarizované ve směru osy x. Mají-li navíc stejnou velikost amplitudy (tj. i intenzitu), platí
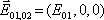 ,
,
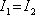 . (5.9)
Pak dostáváme z (5.7) pro intenzitu světla
. (5.9)
Pak dostáváme z (5.7) pro intenzitu světla
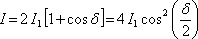 |
(5.10) |
Ve fázovém rozdílu
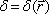 je obsažena prostorová závislost, v různých bodech prostoru je různý fázový rozdíl. Čtverec kosinu může nabývat hodnot od nuly do jedné. Je tedy patrné, že v prostoru, kde se skládají dvě stejně intenzivní vlny, vzniká prostorová modulace intenzity, interferenční obrazec. Intenzita se zde mění od nuly do čtyřnásobku intenzity každého ze svazků. Závislost intenzity je znázorněna na obr. 5.1.
je obsažena prostorová závislost, v různých bodech prostoru je různý fázový rozdíl. Čtverec kosinu může nabývat hodnot od nuly do jedné. Je tedy patrné, že v prostoru, kde se skládají dvě stejně intenzivní vlny, vzniká prostorová modulace intenzity, interferenční obrazec. Intenzita se zde mění od nuly do čtyřnásobku intenzity každého ze svazků. Závislost intenzity je znázorněna na obr. 5.1.
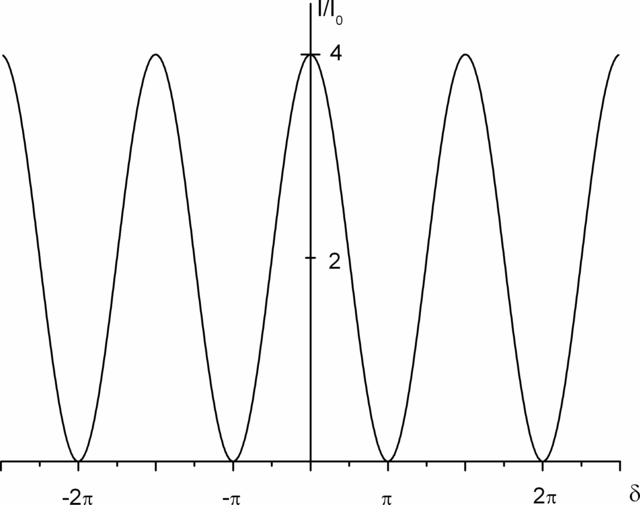 Obr. 5.1
Obr. 5.1 Průběh výsledné intenzity světla v závislosti na fázovém rozdílu
δ mezi dvěma stejně intenzivními interferujícími vlnami.
5.1.1.1 Světelné pole při interferenci dvou rovinných vln
Nyní blíže rozebereme, jaká prostorová struktura výsledného světelného pole vzniká interferencí dvou rovinných vln. Budeme vyšetřovat případ, kdy vlnové vektory obou vln leží v rovině y, z, mají stejné velkosti a svírají úhel
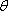 , viz obr. 5.2. Pro jednoduchost opět
, viz obr. 5.2. Pro jednoduchost opět
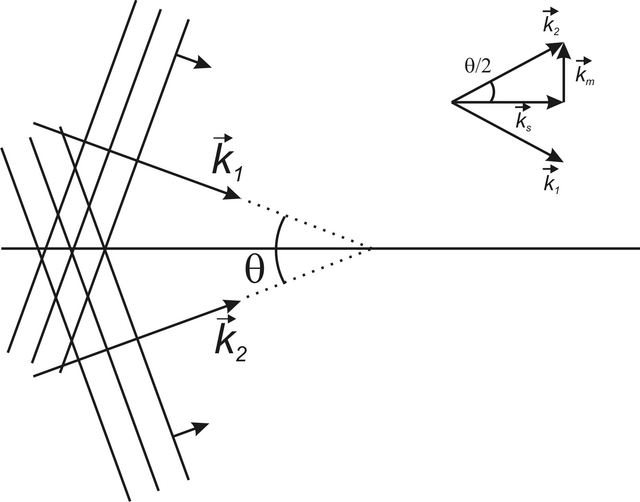 Obr. 5.2
Obr. 5.2 Geometrie interference dvou rovinných vln.
předpokládáme pro obě vlny stejnou amplitudu a lineární polarizaci ve směru osy x,
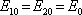 . Vzhledem k symetrii lze očekávat modulaci interferenčního obrazce ve směru kolmém k ose úhlu, který svírají vlny. Tento směr odpovídá směru vektoru
. Vzhledem k symetrii lze očekávat modulaci interferenčního obrazce ve směru kolmém k ose úhlu, který svírají vlny. Tento směr odpovídá směru vektoru
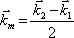 |
(5.11) |
ve směru osy úhlu je vektor
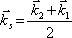 |
(5.12) |
analogicky můžeme zavést fáze

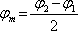 , (5.13)
a
, (5.13)
a
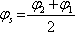 |
(5.14) |
Výsledné pole je tedy rovno (jednotlivé vlny vyjádříme pomocí rov. (5.1) - (5.4))
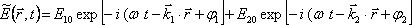 |
(5.15) |
Přímým vyjádřením k1, k2, resp.
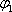 ,
,
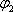 pomocí nově zavedených veličin dostaneme výsledné pole ve tvaru
pomocí nově zavedených veličin dostaneme výsledné pole ve tvaru
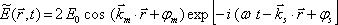 |
(5.16) |
Tento výraz můžeme považovat za složený z "obálky" a "nosné vlny". Výsledné vlnění se tedy šíří ve směru osy úhlu obou vln s vlnovým vektorem
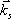 , jehož velikost je podle (5.12) a obr. 5.2 rovna (připomínáme
, jehož velikost je podle (5.12) a obr. 5.2 rovna (připomínáme
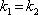 )
)
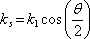 |
(5.17) |
Amplituda této vlny je v kolmém směru periodicky prostorově modulována. Velikost vektoru
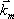 je rovna
je rovna
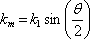 |
(5.18) |
Odpovídající prostorové rozložení intenzity výsledného pole dostaneme podle (5.5),
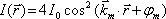 |
(5.19) |
Zde3
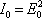 . Tento výsledek souhlasí ovšem s (5.10). Prostorová perioda modulace intenzity je tedy rovna (druhá mocnina kosinu vede ke dvojnásobné frekvenci)
. Tento výsledek souhlasí ovšem s (5.10). Prostorová perioda modulace intenzity je tedy rovna (druhá mocnina kosinu vede ke dvojnásobné frekvenci)
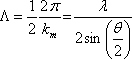 |
(5.20) |
(Tento výsledek, který jsme dostali z rov. (5.5) je přibližný, platí dobře pro malé úhly θ. Interferencí vzniklé elektromagnetické pole totiž není již rovinnou vlnou. Výsledný Poyntingův vektor, jak můžeme zjistit přímým výpočtem, má směr vektoru
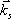 a jeho velikost má časovou střední hodnota (odpovídající podle definice intenzitě světla)
a jeho velikost má časovou střední hodnota (odpovídající podle definice intenzitě světla)
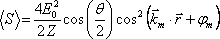 . Tento výraz se liší od rov. (5.19) faktorem
. Tento výraz se liší od rov. (5.19) faktorem
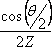 . Kromě toho, že v této kapitole pokládáme
. Kromě toho, že v této kapitole pokládáme
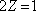 , je tento faktor důsledkem použití přibližného vztahu pro výpočet intenzity. Pro malé úhly θ je
, je tento faktor důsledkem použití přibližného vztahu pro výpočet intenzity. Pro malé úhly θ je
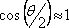 a rozdíl v hodnotě maximální intenzity zanedbatelný.)
a rozdíl v hodnotě maximální intenzity zanedbatelný.)
Interference dvou (téměř) rovinných vln se využívá například při přípravě holografických mřížek, kdy se umístí fotocitlivá deska kolmo na směr osy dvou vln, a prostorová modulace intereferenčního pole vede k periodicky modulované expozici vrstvy. Po vyvolání tak vznikne optická difrakční mřížka, která se používá například ve spektroskopii.
Speciální případ nastává, kdy dvě rovinné vlny postupují proti sobě, tedy pro případ
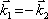 . Pak ovšem
. Pak ovšem
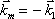 ,
,
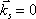 . Nulová hodnota vlnového vektoru ks znamená, že se nejedná o postupnou vlnu, výsledné vlnění se nazývá stojatá vlna. Amplituda stojaté vlny je i tomto případě modulována ve směru daném směrem vektoru
. Nulová hodnota vlnového vektoru ks znamená, že se nejedná o postupnou vlnu, výsledné vlnění se nazývá stojatá vlna. Amplituda stojaté vlny je i tomto případě modulována ve směru daném směrem vektoru
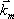 , který je ovšem kolineární se směrem šíření vln. Místa, kde je amplituda pole nulová, se nazývají uzly, místa kde dosahuje maximální hodnoty se nazývají kmitny. Vzdálenost uzlů (kmiten) je
, který je ovšem kolineární se směrem šíření vln. Místa, kde je amplituda pole nulová, se nazývají uzly, místa kde dosahuje maximální hodnoty se nazývají kmitny. Vzdálenost uzlů (kmiten) je
 . Polohy uzlů elektrického a magnetického pole navzájem posunuty o
. Polohy uzlů elektrického a magnetického pole navzájem posunuty o
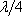 , tj. uzly magnetického pole odpovídají kmitnám pole elektrického. Stojatá optická vlna vzniká často interferencí dopadající a odražené vlny (například od zrcadla). V takovém případě je na odrazné ploše uzel elektrického pole a kmitna magnetického pole.
, tj. uzly magnetického pole odpovídají kmitnám pole elektrického. Stojatá optická vlna vzniká často interferencí dopadající a odražené vlny (například od zrcadla). V takovém případě je na odrazné ploše uzel elektrického pole a kmitna magnetického pole.
2.1.2 Youngův experiment
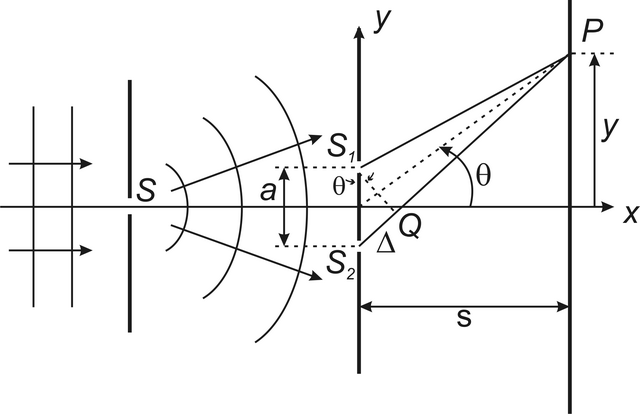 Obr. 5.3
Obr. 5.3 Schéma Youngova experimentu.
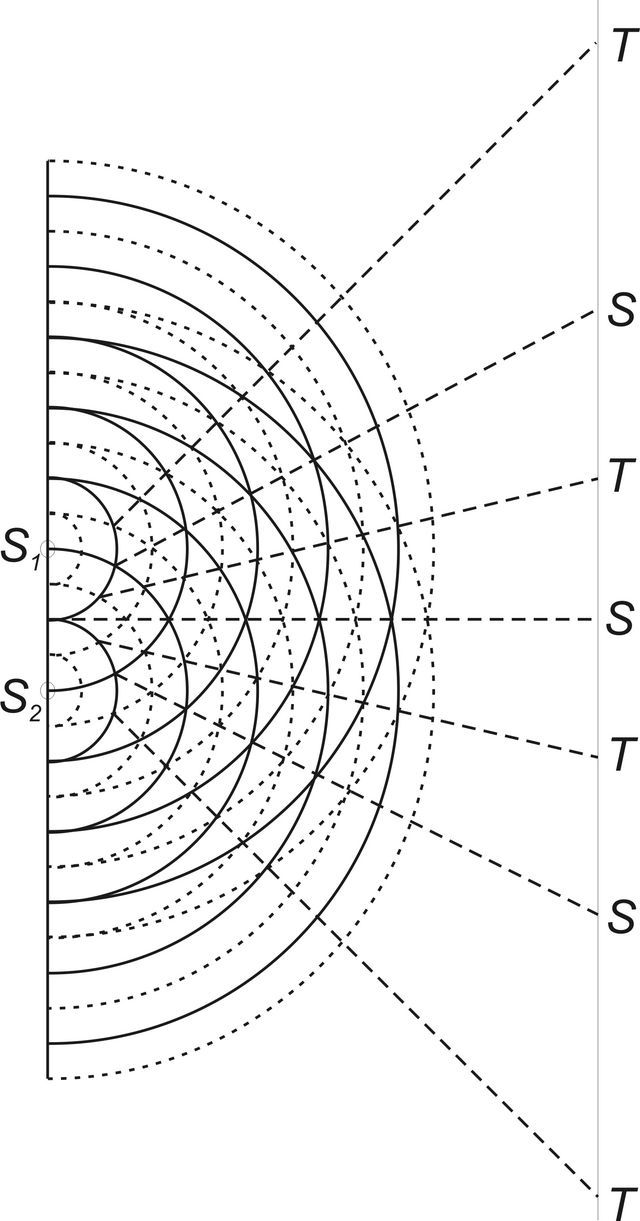 Obr. 5.4
Obr. 5.4 Youngův experiment: Střídání míst s velkou (S) a malou (T) intenzitou světla
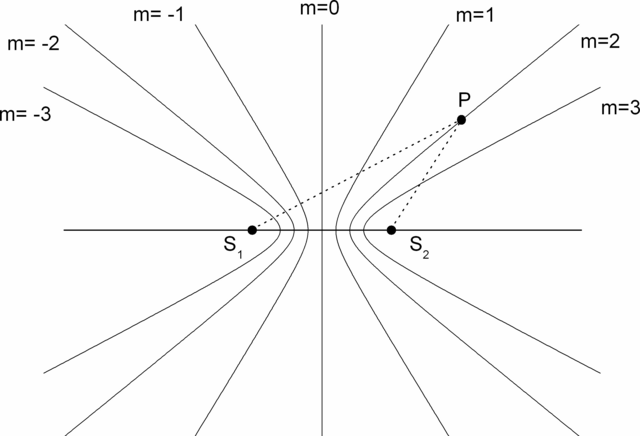 Obr. 5.5
Obr. 5.5 Youngův experiment: Poloha světlých proužků pro určitou velikost dráhového rozdílu
mλ určuje hyperbolickou plochu
Interferenci dvou svazků lze pozorovat v řadě experimentálních uspořádání. Nejznámější je pravděpodobně Youngův pokus (Thomas Young, 1802), jehož uspořádání je schematicky znázorněno na obr. 5.3. Ve stínítku jsou dva malé otvory, které jsou v malé vzdálenosti od sebe a osvětleny tak, aby byly zdrojem vln, které jsou navzájem koherentní (viz dále). To je například splněno tehdy, pokud fáze a amplitudy vln vycházejících z otvorů mají stejné amplitudy a fáze. Toho je možné dosáhnout tím, že stínítko je osvětleno laserovým svazkem, nebo - jako v původním Youngově uspořádání - je použito kvazimonochromatické světlo termického zdroje, kterým se osvětlí otvor S v jiném stínítku, jež je nastaveno tak, že první otvor je umístěn symetricky mezi oběma dalšími otvory. To znamená, že sférická vlna, která vychází z prvního otvoru dopadá na oba otvory ve fázi a ty jsou pak zdroji světla, které může interferovat.
Uvažujme tedy geometrické uspořádání Youngova experimentu podle obr. 5.3. Téměř bodové zdroje světla S1, S2 vyzařují sférické vlny, které se šíří v poloprostoru za stínítkem. Obě pole interferují a v celém prostoru vzniká interferenční pole. V bodech prostoru, kde se vlny (s nulovým relativním fázovým posuvem v otvorech,
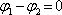 ) setkávají "ve fázi", tj. tak, že jejich vzájemný fázový posuv
) setkávají "ve fázi", tj. tak, že jejich vzájemný fázový posuv
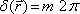 , je velká intenzita světla. Například na ose mezi oběma otvory dopadají obě vlny po průchodu stejně dlouhou dráhou, jejich dráhový (tj. i fázový) rozdíl je tudíž nulový. Vznik tmavých a světlých míst je znázorněn schematicky na obr. 5.4. Geometrické místo bodů, kde je intenzita maximální, je tedy dáno podmínkou, že dráhový rozdíl obou svazků je
, je velká intenzita světla. Například na ose mezi oběma otvory dopadají obě vlny po průchodu stejně dlouhou dráhou, jejich dráhový (tj. i fázový) rozdíl je tudíž nulový. Vznik tmavých a světlých míst je znázorněn schematicky na obr. 5.4. Geometrické místo bodů, kde je intenzita maximální, je tedy dáno podmínkou, že dráhový rozdíl obou svazků je
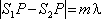 |
(5.21) |
Toto je rovnice hyperbolických ploch, jak jsou znázorněny na obr. 5.5. V blízkosti osy jsou na stínítku přibližně ekvidistantní proužky.
2.1.2.1 Vzdálenost interferenčních proužků v Youngově pokusu blízko osy
V blízkosti osy z je úhel θ malý, proto
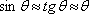 . Podle obr. 5.3 je zřejmé, že pro velkou vzdálenost stínítka od štěrbin je rozdíl drah pro m-té maximum
. Podle obr. 5.3 je zřejmé, že pro velkou vzdálenost stínítka od štěrbin je rozdíl drah pro m-té maximum
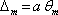 ,
,
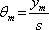 . Podmínka pro maxima je
. Podmínka pro maxima je
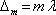 , odtud
, odtud
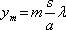 . Rozdíl mezi polohami následujících maxim je zřejmě konstantní, roven
. Rozdíl mezi polohami následujících maxim je zřejmě konstantní, roven
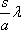 .
.
2.1.3 Další příklady dvojsvazkové interference - dělení vlnoplochy
S interferencí dvou vln (svazků) se setkáváme v řadě dalších případů - ať již v různých optických uspořádáních nebo v každodenním životě. Dva interferující svazky zpravidla vzniknou dělením jednoho svazku (i když je možné pozorovat interferenci svazků vycházejících ze dvou laserů). Podle toho, jak dva svazky vzniknou, se dělí uspořádání pro pozorování interference na případy s dělením amplitudy a na případy s dělením vlnoplochy.
Dva příklady experimentálních uspořádání s dělením vlnoplochy, jak se často uvádějí v učebnicích, jsou uvedeny na obr. 5.6 a 5.7. Jedná se o Billetovu dvojčočku a Lloydovo zrcadlo. Billetova dvojčočka je tvořena dvěma částmi čočky, mezi nimiž je neprůhledná překážka. Bodový zdroj světla S0 je zobrazen každou částí čočky, vzniknou (reálné) obrazy S1 a S2. Vlny vycházející z těchto dvou zdrojů interferují ve vyšrafované oblasti.U Lloydova zrcadla vzniká při odrazu (virtuální) obraz S1 zdroje S0 a dochází k interferenci vln zdrojů S1 a S0 ve vyšrafované oblasti.
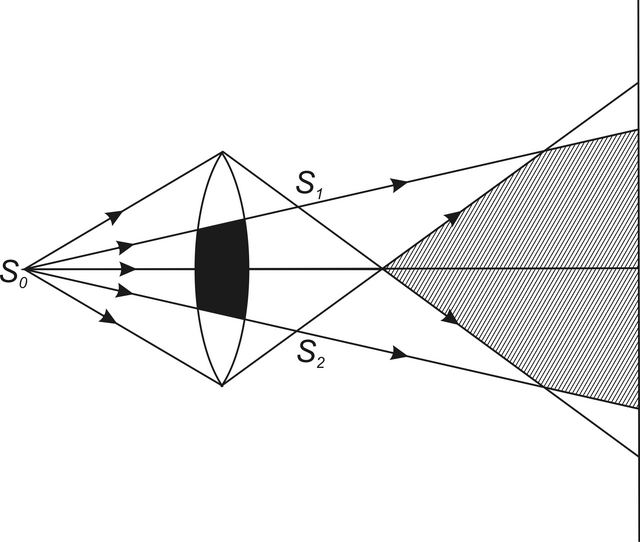 Obr. 5.6
Obr. 5.6 Billetova dvojčočka
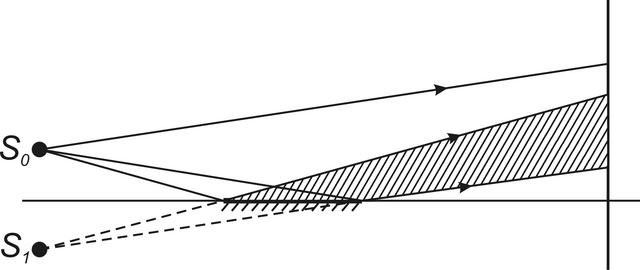 Obr. 5.7
Obr. 5.7 Lloydovo zrcadlo
2.1.4 Další příklady dvojsvazkové interference - dělení amplitudy
2.1.4.1 Michelsonův interferometr
Jak je zřejmé, jsou interferenční obrazce závislé silně na vlnové délce světla. Je proto možné interferenční jevy používat ke studiu spektrálních vlastností světla. Zařízení, které studuje vlastnosti světla na základě jeho interference, tedy studuje kvantitativně interferenci, se nazývá interferometrem.
Velmi známým dvojsvazkovým interferometrem je Michelsonův interferometr, který je znázorněn na obr. 5.8. Byl zkonstruován Albertem Michelsonem v roce 1881. Sehrál důležitou roli ve vývoji fyziky. Kromě jiného Michelson a Morley použili tento interferometr ke konci 19. století ve svém klasickém experimentu, který patří k nejvýznamnějším pokusům v historii fyziky. Ukázali, že není žádný rozdíl v rychlosti světla ve dvou navzájem kolmých směrech, což vedlo k formulaci obecného principu, podle nějž je rychlost světla konstantní ve všech směrech, nezávislá na rychlosti pohybu zdroje světla. Je to jeden z principů Einsteinovy teorie relativity.
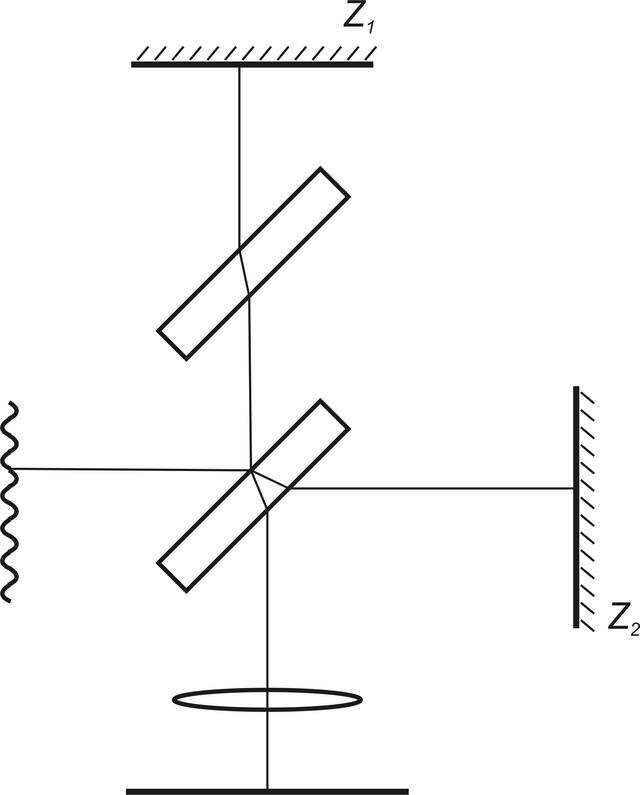 Obr. 5.8
Obr. 5.8 Michelsonův inteferometr
Interferometr patří k uspořádáním s dělením amplitudy. Světlo ze zdroje dopadá na dělič svazku (tenký dielektrický nebo kovový film na povrchu skleněné desky), kde se rozdělí na dva svazky stejné intenzity. Ty se odrážejí na zrcadlech Z1a Z2, postupují pak v obráceném směru, na děliči svazku se opět setkávají a vystupují směrem na stínítko. Setkávají se ovšem se vzájemným fázovým zpožděním, které odpovídá rozdílu optických drah obou paprsků. Jedno ze zrcadel je na posuvném zařízení, takže je možné měnit optickou dráhu světla v jednom rameni, lze nastavovat náklon zrcadel. Svazek, který postupuje na obr. 5.8 horizontálně, prochází deskou děliče svazku třikrát, zatímco druhý svazek prochází deskou jen jednou. V některých případech, když se užívá bílé světlo, je nezbytné, aby optické dráhy obou svazků byly stejné. To lze sice zařídit posuvem jednoho ze zrcadel, ale velikost posuvu je závislá na vlnové délce. Proto se zpravidla užívá kompenzační desky, která je vyrobena ze stejného materiálu, jako dělič svazku. V případě, že interferometrem procházejí rovinné vlny dopadající kolmo na plochy zrcadel, je stínítko rovnoměrně osvětlené, intenzita osvětleni se mění se vzájemným fázovým posuvem svazků podle vztahu (5.10). Pokud se jedno ze zrcadel skloní, objeví se na stínítku soustava rovnoběžných světlých a tmavých interferenčních proužků (tzv. proužky stejné tloušťky). Pokud interferometrem prochází divergentní vlny, jako v případě plošného zdroje, vzniká na stínítku soustava soustředných kruhů. Tento případ odpovídá vzniku kroužků stejného sklonu.
2.1.4.2 Interference na dielektrických vrstvách
Představme si, že monochromatická vlna dopadá na planparalelní dielektrickou vrstvu (sklíčko, mýdlová blána). Pro pozorování interference v bílém (nekoherentním světle - viz další kapitola), je nutné aby vrstva byla tenká, s tloušťkou nepřesahující příliš délku vlny světla. Oba povrchy filmu částečně odrážejí a propouštějí světlo. Vypočítáme nyní fázový rozdíl mezi paprsky, které se odrážejí od vrchní plochy, a paprsky, které se odrážejí od spodní plochy a vycházejí zpět nahoru. Situace je schematicky znázorněna na obr. 5.9. Úhel dopadu, resp. lomu je
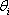 , resp.
, resp.
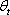 . Tloušťka filmu je h, index lomu filmu je
. Tloušťka filmu je h, index lomu filmu je
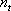 , index lomu okolního prostředí (vzduchu například) je
, index lomu okolního prostředí (vzduchu například) je
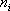 . Urazí-li světlo dráhu z, změní se jeho fáze ("náběh fáze") o
. Urazí-li světlo dráhu z, změní se jeho fáze ("náběh fáze") o
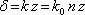 |
(5.22) |
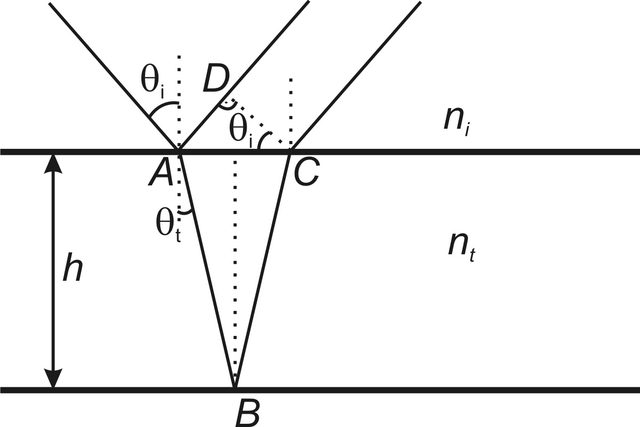 Obr. 5.9
Obr. 5.9 Výpočet fázového rozdílu dvou svazků interferujících při odrazu na planparalelní desce (filmu)
kde
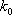 je velikost vlnového vektoru ve vakuu a n je index lomu prostředí, ve kterém se světlo šíří. Je výhodné zavést optickou dráhu, kterou budeme označovat indexem OD, která je definována jako součin dráhy geometrické a indexu lomu:
je velikost vlnového vektoru ve vakuu a n je index lomu prostředí, ve kterém se světlo šíří. Je výhodné zavést optickou dráhu, kterou budeme označovat indexem OD, která je definována jako součin dráhy geometrické a indexu lomu:
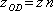 |
(5.23) |
Náběh fáze je pak
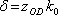 |
(5.24) |
Rozdíl optických drah mezi paprskem 1 a 2 na obr. 5.8 je
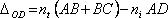 |
(5.25) |
Z geometrie plyne
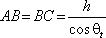 |
(5.26) |
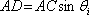 |
(5.27) |
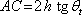 |
(5.28) |
Dosazením (5.14) do (5.13) máme
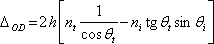 |
(5.29) |
Vyjádříme-li sin
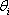 pomocí zákona lomu, dostaneme
pomocí zákona lomu, dostaneme
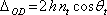 |
(5.30) |
Fázový rozdíl mezi oběma svazky je tedy
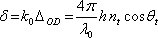 |
(5.31) |
Pro závěry o průběhu interference je si ovšem třeba uvědomit, že paprsky mohou získávat dodatečný fázový posun
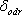 při odrazu na horní a spodní ploše tvořící film (viz Fresnelovy vzorce). Pokud jde například o vrstvu oleje na hladině vody, jedná se u obou odrazů o rozhraní z prostředí opticky řidšího do prostředí opticky hustšího (vzduch-olej-voda) a změna fáze při odrazu je v obou případech stejná. Stejně je tomu v opačném případě (oba odrazy od rozhraní mezi opticky hustším a řidším prostředím). V těchto případech je
při odrazu na horní a spodní ploše tvořící film (viz Fresnelovy vzorce). Pokud jde například o vrstvu oleje na hladině vody, jedná se u obou odrazů o rozhraní z prostředí opticky řidšího do prostředí opticky hustšího (vzduch-olej-voda) a změna fáze při odrazu je v obou případech stejná. Stejně je tomu v opačném případě (oba odrazy od rozhraní mezi opticky hustším a řidším prostředím). V těchto případech je
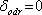 . Obecně ovšem může být dodatečný fázový posuv nenulový, jako v případě rozhraní vzduch-sklo-vzduch, kdy rozdíl fází, který vznikne mezi oběma svazky je
. Obecně ovšem může být dodatečný fázový posuv nenulový, jako v případě rozhraní vzduch-sklo-vzduch, kdy rozdíl fází, který vznikne mezi oběma svazky je
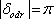 . Podmínku maxima interference v odraženém světle je proto možné v uvažovaných případech psát
. Podmínku maxima interference v odraženém světle je proto možné v uvažovaných případech psát
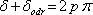 |
(5.32) |
kde p je celé číslo. Podmínka pro minimum je
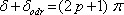 |
(5.33) |
Na obr. 5.10 je znázorněn případ interference, který vzniká dělením amplitudy vlny generované bodovým zdrojem světla S0. Fresnelovými odrazy na plochách desky vznikají dva virtuální zdroje S1, S2. Dvě kulové vlny vycházející z těchto zdrojů interferují v celém prostoru nad deskou, interferenční proužky jsou delokalizované.
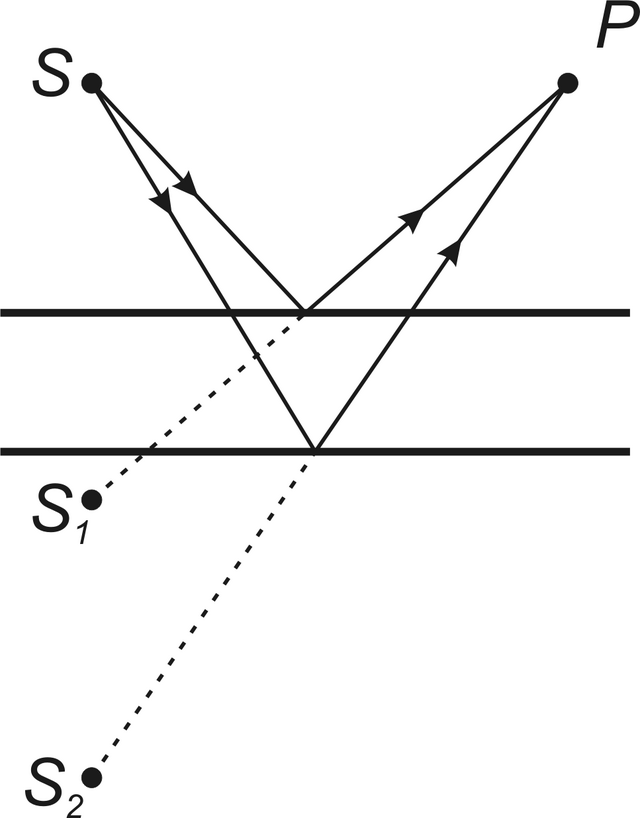 Obr. 5.10
Obr. 5.10 Interference na planparalelní tenké vrstvě - bodový zdroj světla
2.1.4.2.1 Proužky stejného sklonu
Často se setkáváme s plošným zdrojem světla, který je možné si představit jako soubor nezávislých bodových zdrojů světla. Pokud je zdroj kvazimonochromatický, každý z bodových zdrojů vyzařuje na stejné frekvenci, ale bez vzájemných fázových vztahů. Každý bodový zdroj vytváří svoje interferenční pole a výsledné interferenční pole je dáno součtem polí jednotlivých zdrojů. Jinými slovy, vlny vycházející z různých bodových zdrojů spolu neinterferují. Při pozorování interference s plošným zdrojem budou interferenční proužky pozorovatelné tam, kde poloha a vzdálenost jednotlivých proužků není ovlivněna polohou jednotlivých bodů plošného zdroje. Například nulový rozdíl optických drah odpovídá světlému proužku. V určitém místě, kde je nulový rozdíl optických drah nezávisle na poloze bodového zdroje, bude světlý proužek tvořen interferencí všech bodů plošného zdroje - bude dobrý kontrast. Obecně platí, že dobrý kontrast proužků v případě plošného zdroje bude v oblasti, kde je rozdíl optických drah mezi interferujícími svazky malý.
Osvětlení planparalelní desky (filmu) plošným zdrojem je znázorněno na obr. 5.11. Je zřejmé, že v každém bodě prostoru budou interferovat paprsky z různých bodů plošného zdroje, a to vždy s různými vzájemnými fázovými rozdíly, protože rozdíl optických
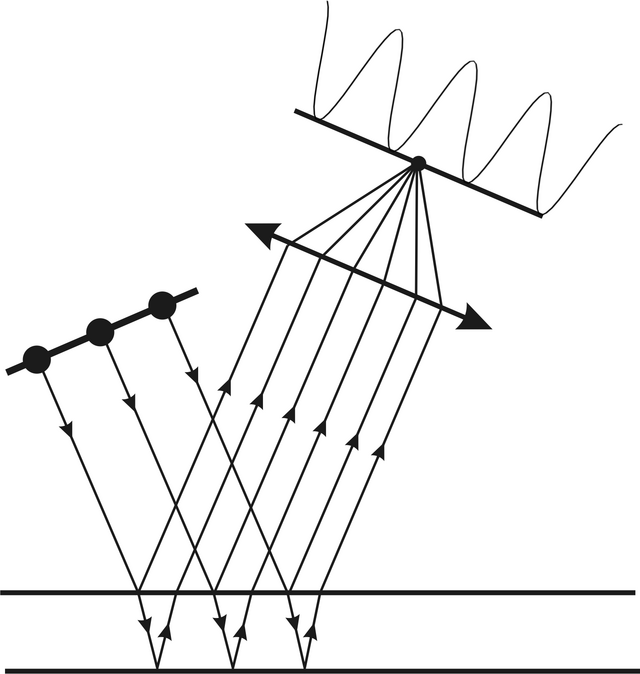 Obr. 5.11
Obr. 5.11 Interference světla na planparalelním filmu - plošný zdroj světla
drah závisí na úhlu dopadu (rov. 5.31). Umístíme-li však do odraženého světla čočku, budou se v každém bodě její ohniskové roviny setkávat paprsky, které vycházejí z desky pod stejným úhlem. Těmto navzájem rovnoběžným vycházejícím paprskům odpovídají ovšem rovnoběžné dopadající paprsky, z nichž každý se rozdělí na rozhraní na dva. Každý pár paprsků pak interferuje (se stejným fázovým rozdílem) v bodě na stínítku. Výsledkem je interferenční obrazec s vysokým kontrastem. Interferenční proužky není možné pozorovat všude v prostoru, ale jen pomocí čočky v její ohniskové rovině. Interferenční proužky jsou proto lokalizované, v ohniskové rovině čočky, tedy v nekonečnu. Takto vznikajícím proužkům se říká též proužky (nebo kroužky - podle geometrického tvaru) stejného sklonu, protože určitý proužek odpovídá určitému sklonu dopadajících rovnoběžných paprsků. Nazývají se také Haidingerovy kroužky. Paprsky dopadající pod určitým úhlem vůči normále, jak je znázorněno na obrázku, jsou fokusovány do určitého bodu v ohniskové rovině. Při dostatečně velkých rozměrech plošného zdroje dopadají paprsky ze všech stran a body v ohniskové rovině, do kterých se zobrazí, leží na kružnici. Vznikají tak interferenční kroužky.
2.1.4.2.2 Proužky stejné tloušťky
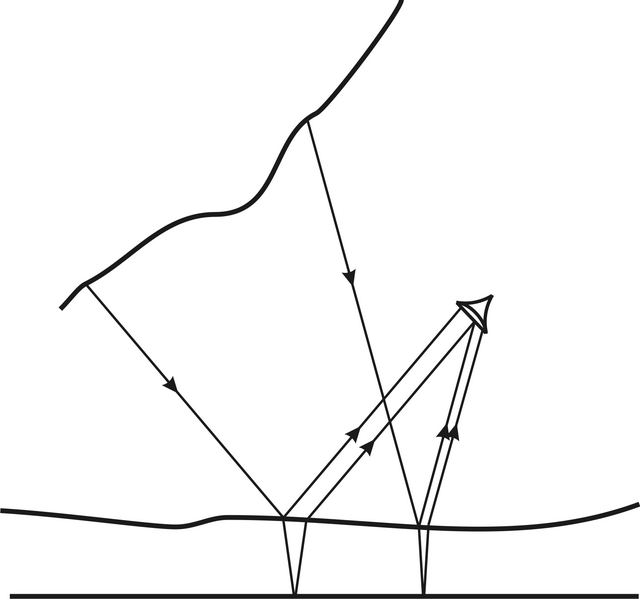 Obr. 5.12
Obr. 5.12 Pozorování proužků stejné tloušťky (obrazy
A,
B v oku odpovídají různým místům na vrstvě)
Pokud je tloušťka filmu proměnná, mění se fázový rozdíl mezi dvojicí interferujících svazků (vznikajících štěpením paprsku z určitého bodu zdroje) nejen na úhlu, ale také na tloušťce filmu (viz vztah 5.31). Když je ovšem směr paprsků pevný (například kolmý dopad), objeví se tmavé a světlé proužky podle příslušného fázového rozdílu daného tloušťkou filmu v určitém místě. Interferenční proužky se pak nazývají proužky stejné tloušťky. Možné uspořádání pro jejich pozorování na klínovitém filmu je znázorněno na obr. 5.12. Dvojice interferujících paprsků (vycházejících z jednoho bodu zdroje) po odrazu z obou ploch filmu se při vzdalování rozbíhá - nevznikají proto reálné - delokalizované proužky, ale proužky virtuální, které je možné vidět okem. Jak je znázorněno na obr. 5.12, oko zaostřené na povrch filmu fokusuje dvojice paprsků, vybírá místo na povrchu filmu a (svou polohou a malým průměrem vstupní pupily) směr paprsků. Proužky jsou lokalizované na povrchu filmu, nazývají se také Fizeauovy proužky.
Pokud je tenký film osvětlen zdrojem bílého světla, může se film jevit jako zbarvený, jak můžeme pozorovat například u olejových skvrn na loužích. V určité části filmu může být jeho tloušťka taková, že dochází ke konstruktivní interferenci pro vlnové délky z červené části spektra s dráhovým rozdílem určitého počtu vlnových délek,

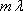 . Pokud interference pro
. Pokud interference pro
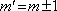 odpovídá vlnovým délkám mimo viditelnou oblast světla, jeví se film červený. Tato situace je jistě splněna, pokud je m malé, tedy optická tloušťka filmu je srovnatelná s vlnovou délkou světla.
odpovídá vlnovým délkám mimo viditelnou oblast světla, jeví se film červený. Tato situace je jistě splněna, pokud je m malé, tedy optická tloušťka filmu je srovnatelná s vlnovou délkou světla.
2.1.4.2.3 Antireflexní vrstvy (protiodrazné vrstvy)
S interferencí na tenkých filmech se setkáváme běžně u antireflexních vrstev, kterými se pokrývají čočky fotografických aparátů nebo brýlí. Cílem použití těchto vrstev je minimalizovat ztráty procházejícího světelného toku způsobené odrazem na rozhraní vzduch - sklo (fresnelovské ztráty). U objektivů tvořených řadou (někdy třeba 20) čoček mohou být tyto ztráty značné, u brýlí hraje roli i potlačení odrazů pozorovaných jinými osobami
(i estetický faktor). Antireflexní vrstvu je možné vytvořit z materiálu, který ve viditelné oblasti neabsorbuje. Na povrchu skla se vytvoří vrstva vhodné tloušťky h, tak, aby se vlny odražené na jejím horním a dolním rozhraní vzájemnou interferencí vyrušily. Jsou-li indexy lomu vzduchu nv , filmu nf, a skla ns takové, že nv < nf < ns, je možné zvolit čtvrtvlnovou tloušťku vrstvy. Skutečně, pro uvedené velikosti indexů lomu při odrazu nedochází ke změně fáze (
 ) a podmínka pro minimum (5.33) spolu s (5.31) dává pro
) a podmínka pro minimum (5.33) spolu s (5.31) dává pro
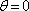
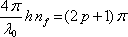 |
(5.34) |
Nejmenší tloušťka vrstvy je tedy (
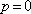 )
)
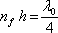 |
(5.35) |
Aby byla odražená vlna skutečně nulová, musí být intenzita v interferenčním minimu nulová, tedy amplitudy obou odražených stejné. Znamená to (viz (3-39) a (3-63))
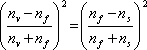 |
(5.36) |
neboli
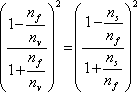 |
(5.37) |
Na obou stranách této rovnosti jsou stejné funkce, rovny si mohou být pouze, pokud
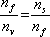 |
(5.38) |
Odtud dostáváme podmínku pro index lomu antireflexní vrstvy
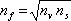 |
(5.39) |
Například pro
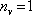 ,
,
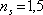 vychází
vychází
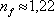 . Používá se například vrstva MgF2 s blízkým indexem lomu 1,38. Nedojde ovšem k úplnému potlačení odrazu. Její minimální tloušťka podle (5.35) vychází asi 110 nm.
. Používá se například vrstva MgF2 s blízkým indexem lomu 1,38. Nedojde ovšem k úplnému potlačení odrazu. Její minimální tloušťka podle (5.35) vychází asi 110 nm.
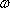 . Popíšeme je pomocí komplexní reprezentace (
. Popíšeme je pomocí komplexní reprezentace (
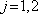 )
)
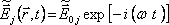
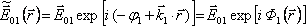
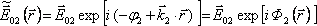
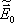 dostaneme podle (5.1). V této kapitole budeme při vyšetřování interferenčních jevů, jak je často zvykem, vyjadřovat intenzitu
dostaneme podle (5.1). V této kapitole budeme při vyšetřování interferenčních jevů, jak je často zvykem, vyjadřovat intenzitu
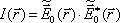
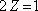 , protože se zabýváme spíše modulací intenzity v prostředí se stejnou impedancí než její skutečnou hodnotou.
, protože se zabýváme spíše modulací intenzity v prostředí se stejnou impedancí než její skutečnou hodnotou.
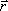 , pro přehlednost argumenty nevypisujeme) pro výslednou intenzitu světla v určitém místě daném polohovým vektorem
, pro přehlednost argumenty nevypisujeme) pro výslednou intenzitu světla v určitém místě daném polohovým vektorem
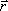
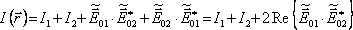
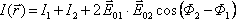
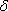 ,
,
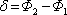
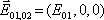 ,
,
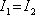 . (5.9)
Pak dostáváme z (5.7) pro intenzitu světla
. (5.9)
Pak dostáváme z (5.7) pro intenzitu světla
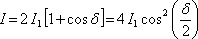
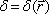 je obsažena prostorová závislost, v různých bodech prostoru je různý fázový rozdíl. Čtverec kosinu může nabývat hodnot od nuly do jedné. Je tedy patrné, že v prostoru, kde se skládají dvě stejně intenzivní vlny, vzniká prostorová modulace intenzity, interferenční obrazec. Intenzita se zde mění od nuly do čtyřnásobku intenzity každého ze svazků. Závislost intenzity je znázorněna na obr. 5.1.
je obsažena prostorová závislost, v různých bodech prostoru je různý fázový rozdíl. Čtverec kosinu může nabývat hodnot od nuly do jedné. Je tedy patrné, že v prostoru, kde se skládají dvě stejně intenzivní vlny, vzniká prostorová modulace intenzity, interferenční obrazec. Intenzita se zde mění od nuly do čtyřnásobku intenzity každého ze svazků. Závislost intenzity je znázorněna na obr. 5.1.

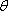 , viz obr. 5.2. Pro jednoduchost opět
, viz obr. 5.2. Pro jednoduchost opět

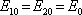 . Vzhledem k symetrii lze očekávat modulaci interferenčního obrazce ve směru kolmém k ose úhlu, který svírají vlny. Tento směr odpovídá směru vektoru
. Vzhledem k symetrii lze očekávat modulaci interferenčního obrazce ve směru kolmém k ose úhlu, který svírají vlny. Tento směr odpovídá směru vektoru
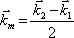
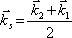

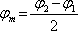 , (5.13)
a
, (5.13)
a
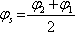
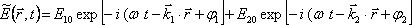
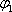 ,
,
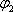 pomocí nově zavedených veličin dostaneme výsledné pole ve tvaru
pomocí nově zavedených veličin dostaneme výsledné pole ve tvaru
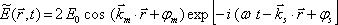
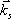 , jehož velikost je podle (5.12) a obr. 5.2 rovna (připomínáme
, jehož velikost je podle (5.12) a obr. 5.2 rovna (připomínáme
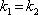 )
)
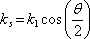
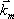 je rovna
je rovna
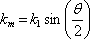
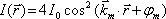
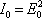 . Tento výsledek souhlasí ovšem s (5.10). Prostorová perioda modulace intenzity je tedy rovna (druhá mocnina kosinu vede ke dvojnásobné frekvenci)
. Tento výsledek souhlasí ovšem s (5.10). Prostorová perioda modulace intenzity je tedy rovna (druhá mocnina kosinu vede ke dvojnásobné frekvenci)
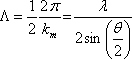
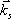 a jeho velikost má časovou střední hodnota (odpovídající podle definice intenzitě světla)
a jeho velikost má časovou střední hodnota (odpovídající podle definice intenzitě světla)
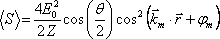 . Tento výraz se liší od rov. (5.19) faktorem
. Tento výraz se liší od rov. (5.19) faktorem
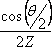 . Kromě toho, že v této kapitole pokládáme
. Kromě toho, že v této kapitole pokládáme
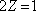 , je tento faktor důsledkem použití přibližného vztahu pro výpočet intenzity. Pro malé úhly θ je
, je tento faktor důsledkem použití přibližného vztahu pro výpočet intenzity. Pro malé úhly θ je
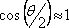 a rozdíl v hodnotě maximální intenzity zanedbatelný.)
a rozdíl v hodnotě maximální intenzity zanedbatelný.)
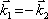 . Pak ovšem
. Pak ovšem
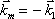 ,
,
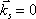 . Nulová hodnota vlnového vektoru ks znamená, že se nejedná o postupnou vlnu, výsledné vlnění se nazývá stojatá vlna. Amplituda stojaté vlny je i tomto případě modulována ve směru daném směrem vektoru
. Nulová hodnota vlnového vektoru ks znamená, že se nejedná o postupnou vlnu, výsledné vlnění se nazývá stojatá vlna. Amplituda stojaté vlny je i tomto případě modulována ve směru daném směrem vektoru
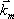 , který je ovšem kolineární se směrem šíření vln. Místa, kde je amplituda pole nulová, se nazývají uzly, místa kde dosahuje maximální hodnoty se nazývají kmitny. Vzdálenost uzlů (kmiten) je
, který je ovšem kolineární se směrem šíření vln. Místa, kde je amplituda pole nulová, se nazývají uzly, místa kde dosahuje maximální hodnoty se nazývají kmitny. Vzdálenost uzlů (kmiten) je
 . Polohy uzlů elektrického a magnetického pole navzájem posunuty o
. Polohy uzlů elektrického a magnetického pole navzájem posunuty o
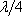 , tj. uzly magnetického pole odpovídají kmitnám pole elektrického. Stojatá optická vlna vzniká často interferencí dopadající a odražené vlny (například od zrcadla). V takovém případě je na odrazné ploše uzel elektrického pole a kmitna magnetického pole.
, tj. uzly magnetického pole odpovídají kmitnám pole elektrického. Stojatá optická vlna vzniká často interferencí dopadající a odražené vlny (například od zrcadla). V takovém případě je na odrazné ploše uzel elektrického pole a kmitna magnetického pole.



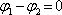 ) setkávají "ve fázi", tj. tak, že jejich vzájemný fázový posuv
) setkávají "ve fázi", tj. tak, že jejich vzájemný fázový posuv
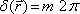 , je velká intenzita světla. Například na ose mezi oběma otvory dopadají obě vlny po průchodu stejně dlouhou dráhou, jejich dráhový (tj. i fázový) rozdíl je tudíž nulový. Vznik tmavých a světlých míst je znázorněn schematicky na obr. 5.4. Geometrické místo bodů, kde je intenzita maximální, je tedy dáno podmínkou, že dráhový rozdíl obou svazků je
, je velká intenzita světla. Například na ose mezi oběma otvory dopadají obě vlny po průchodu stejně dlouhou dráhou, jejich dráhový (tj. i fázový) rozdíl je tudíž nulový. Vznik tmavých a světlých míst je znázorněn schematicky na obr. 5.4. Geometrické místo bodů, kde je intenzita maximální, je tedy dáno podmínkou, že dráhový rozdíl obou svazků je
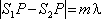
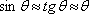 . Podle obr. 5.3 je zřejmé, že pro velkou vzdálenost stínítka od štěrbin je rozdíl drah pro m-té maximum
. Podle obr. 5.3 je zřejmé, že pro velkou vzdálenost stínítka od štěrbin je rozdíl drah pro m-té maximum
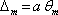 ,
,
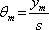 . Podmínka pro maxima je
. Podmínka pro maxima je
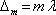 , odtud
, odtud
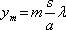 . Rozdíl mezi polohami následujících maxim je zřejmě konstantní, roven
. Rozdíl mezi polohami následujících maxim je zřejmě konstantní, roven
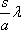 .
.



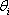 , resp.
, resp.
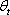 . Tloušťka filmu je h, index lomu filmu je
. Tloušťka filmu je h, index lomu filmu je
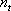 , index lomu okolního prostředí (vzduchu například) je
, index lomu okolního prostředí (vzduchu například) je
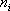 . Urazí-li světlo dráhu z, změní se jeho fáze ("náběh fáze") o
. Urazí-li světlo dráhu z, změní se jeho fáze ("náběh fáze") o
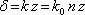

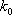 je velikost vlnového vektoru ve vakuu a n je index lomu prostředí, ve kterém se světlo šíří. Je výhodné zavést optickou dráhu, kterou budeme označovat indexem OD, která je definována jako součin dráhy geometrické a indexu lomu:
je velikost vlnového vektoru ve vakuu a n je index lomu prostředí, ve kterém se světlo šíří. Je výhodné zavést optickou dráhu, kterou budeme označovat indexem OD, která je definována jako součin dráhy geometrické a indexu lomu:
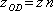
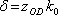
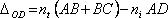
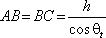
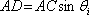
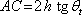
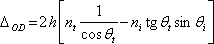
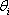 pomocí zákona lomu, dostaneme
pomocí zákona lomu, dostaneme
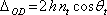
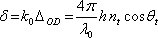
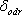 při odrazu na horní a spodní ploše tvořící film (viz Fresnelovy vzorce). Pokud jde například o vrstvu oleje na hladině vody, jedná se u obou odrazů o rozhraní z prostředí opticky řidšího do prostředí opticky hustšího (vzduch-olej-voda) a změna fáze při odrazu je v obou případech stejná. Stejně je tomu v opačném případě (oba odrazy od rozhraní mezi opticky hustším a řidším prostředím). V těchto případech je
při odrazu na horní a spodní ploše tvořící film (viz Fresnelovy vzorce). Pokud jde například o vrstvu oleje na hladině vody, jedná se u obou odrazů o rozhraní z prostředí opticky řidšího do prostředí opticky hustšího (vzduch-olej-voda) a změna fáze při odrazu je v obou případech stejná. Stejně je tomu v opačném případě (oba odrazy od rozhraní mezi opticky hustším a řidším prostředím). V těchto případech je
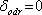 . Obecně ovšem může být dodatečný fázový posuv nenulový, jako v případě rozhraní vzduch-sklo-vzduch, kdy rozdíl fází, který vznikne mezi oběma svazky je
. Obecně ovšem může být dodatečný fázový posuv nenulový, jako v případě rozhraní vzduch-sklo-vzduch, kdy rozdíl fází, který vznikne mezi oběma svazky je
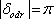 . Podmínku maxima interference v odraženém světle je proto možné v uvažovaných případech psát
. Podmínku maxima interference v odraženém světle je proto možné v uvažovaných případech psát
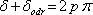
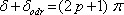




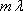 . Pokud interference pro
. Pokud interference pro
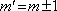 odpovídá vlnovým délkám mimo viditelnou oblast světla, jeví se film červený. Tato situace je jistě splněna, pokud je m malé, tedy optická tloušťka filmu je srovnatelná s vlnovou délkou světla.
odpovídá vlnovým délkám mimo viditelnou oblast světla, jeví se film červený. Tato situace je jistě splněna, pokud je m malé, tedy optická tloušťka filmu je srovnatelná s vlnovou délkou světla.
 ) a podmínka pro minimum (5.33) spolu s (5.31) dává pro
) a podmínka pro minimum (5.33) spolu s (5.31) dává pro
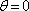
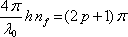
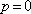 )
)
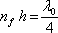
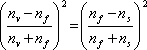
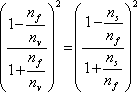
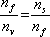
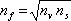
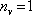 ,
,
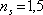 vychází
vychází
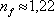 . Používá se například vrstva MgF2 s blízkým indexem lomu 1,38. Nedojde ovšem k úplnému potlačení odrazu. Její minimální tloušťka podle (5.35) vychází asi 110 nm.
. Používá se například vrstva MgF2 s blízkým indexem lomu 1,38. Nedojde ovšem k úplnému potlačení odrazu. Její minimální tloušťka podle (5.35) vychází asi 110 nm.