1.8 Šíření světla ve vodivém prostředí
Uvažujme nyní šíření elektromagnetické harmonické rovinné vlny ve vodivém homogenním izotropním prostředí. Dosadíme-li výraz pro pole v komplexním vyjádření (1.64) do rov. (1.13) a použijeme-li rov. (1.8), dostaneme vlnovou rovnici ve tvaru
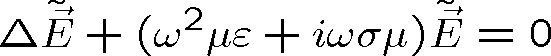 |
(1.88) |
V analogii k rov. (1.42) zavedeme komplexní vlnový vektor, jehož velikost je nyní dána komplexním číslem
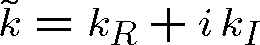 |
(1.89) |
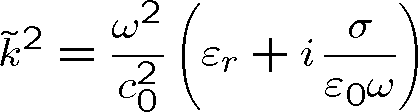 |
(1.90) |
Podobně můžeme zavést komplexní relativní permitivitu
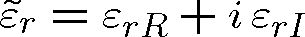 |
(1.91) |
respektive komplexní index lomu
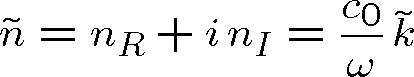 |
(1.92) |
vztahem
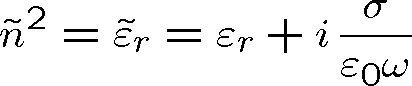 |
(1.93) |
Zde jsme použili obvyklého označení pro reálnou část relativní permitivity,
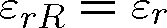 . Vyjádříme-li monochromatickou rovinnou vlnu, která se šíří ve směru osy z, pomocí komplexního vlnového vektoru12, můžeme do rov. (1.64) dosadit rov. (1.89)
. Vyjádříme-li monochromatickou rovinnou vlnu, která se šíří ve směru osy z, pomocí komplexního vlnového vektoru12, můžeme do rov. (1.64) dosadit rov. (1.89)
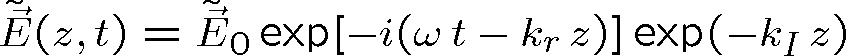 |
(1.94) |
Dostaneme tedy jakousi obdobu rovinné vlny, jejíž amplituda je při šíření v homogenním prostředí tlumena, tj. rovna
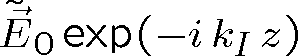 . Vyjádříme-li nyní intenzitu světla podle rov. (1.72) máme
. Vyjádříme-li nyní intenzitu světla podle rov. (1.72) máme
 |
(1.95) |
což je známý Lambertův - Beerův zákon, který popisuje exponenciální tlumení intenzity vlny při šíření - absorpci13. Koeficient a je absorpční koeficient14. Ze vztahu (1.72) mezi intenzitou světla a velikostí elektrické intenzity je zřejmé, že
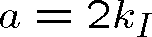 |
(1.96) |
K absorpčnímu zákonu (1.95) se vrátíme ještě v kapitole 14 (vztah (14.50)), průběh intenzity světla daný tímto zákonem je znázorněn na obr. 14.4.
Velikost reálné a imaginární části vlnového vektoru můžeme vyjádřit explicitně. Výraz (1.90) lze psát (zde
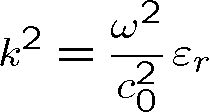 )
)
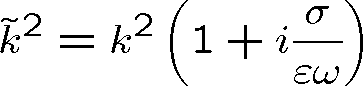 |
(1.97) |
Umocněním rov. (1.89) a dosazením do rov. (1.97) máme
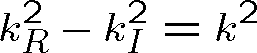 |
(1.98) |
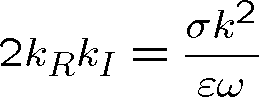 |
(1.99) |
Po umocnění rov. (1.99) můžeme dosadit za
 do rov. (1.98) a získat tak kvadratickou rovnici pro
do rov. (1.98) a získat tak kvadratickou rovnici pro
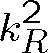 :
:
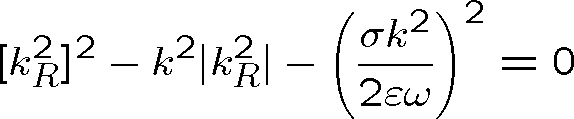 |
(1.100) |
Její řešení je
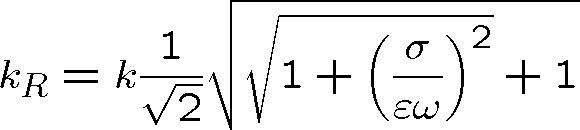 |
(1.101) |
Z rov. (1.99) pak máme
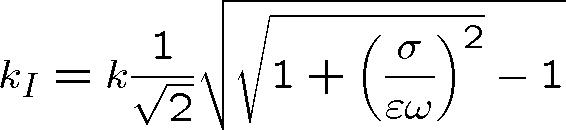 |
(1.102) |
"Běžný" index lomu, tj. reálná část komplexního indexu lomu, jak je vidět porovnáním vztahů (1.89) a (1.92) je roven
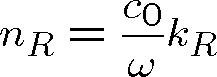 .
Pomocí rov. (1.101) tedy můžeme explicitně psát
.
Pomocí rov. (1.101) tedy můžeme explicitně psát
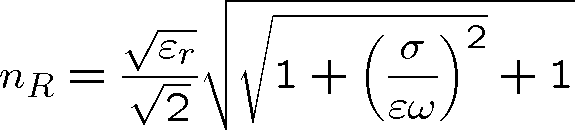 |
(1.103) |
Pro bezztrátová (nevodivá) prostředí, tedy pro
 , dostáváme z tohoto obecného vztahu obvykle používaný (1.16). Z rov. (1.96) a (1.102) můžeme vyjádřit absorpční koeficient. Velmi často je veličina
, dostáváme z tohoto obecného vztahu obvykle používaný (1.16). Z rov. (1.96) a (1.102) můžeme vyjádřit absorpční koeficient. Velmi často je veličina
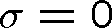 malá, takže lze s dobrou přesností aproximovat odmocninu
malá, takže lze s dobrou přesností aproximovat odmocninu
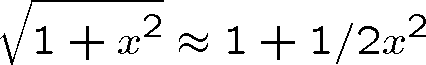 , což vede k obvykle užívanému výrazu pro absorpční koeficient
, což vede k obvykle užívanému výrazu pro absorpční koeficient
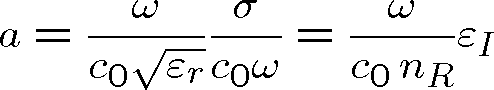 |
(1.104) |
Pozn. 1 Permitivita v látkách je také funkcí frekvence elektromagnetické vlny. Této závislosti se říká disperze a látky se nazývají disperzními. Zde disperzi nebereme v úvahu.
Pozn. 2 Skutečně, platí-li pro homogenní ohmický (tedy
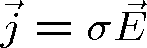 ) vodič rovnice kontinuity proudu,
) vodič rovnice kontinuity proudu,
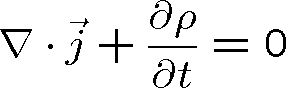 , a rov. (1.3), dostáváme pro hustotu náboje diferenciální rovnici
, a rov. (1.3), dostáváme pro hustotu náboje diferenciální rovnici
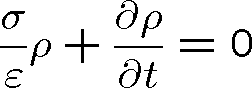 , která má řešení odpovídající exponenciálnímu poklesu:
, která má řešení odpovídající exponenciálnímu poklesu:
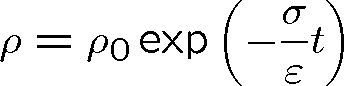 .
Pozn. 3 Je-li například vlna popsána funkcí
.
Pozn. 3 Je-li například vlna popsána funkcí
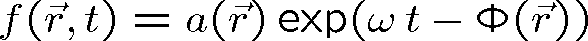 , je plocha konstantní amplitudy dána rovnicí
, je plocha konstantní amplitudy dána rovnicí
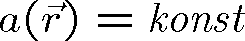 , vlnoplocha rovnicí
, vlnoplocha rovnicí
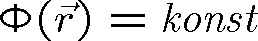 . Vlny, pro něž si vlnoplochy a plochy konstantní amplitudy neodpovídají, se nazývají nehomogenní.
Pozn. 4 Název "rovinné vlny" se obvykle užívá pro "homogenní rovinné vlny", které uvažujeme také zde.
Pozn. 5 Ze vztahů (1.35, 1.36) plyne, že pro nulovou hodnotu elektrického pole E je nulová i hodnota magnetického pole B, tj. obě pole jsou v postupující elektromagnetické rovinné vlně ve fázi.
Pozn. 6 Harmonickou vlnu lze ekvivalentně popsat jak funkcí sinus tak funkcí kosinus, které se liší jen fázovým posuvem. Dáváme zde přednost funkci cos.
Pozn. 7 V této poznámce použijeme komplexní reprezentaci vln, jak bude zavedena v odstavci 1.5. V optice se často setkáváme se situací, kdy postupuje v určitém směru (osa z) vlna, která se málo liší od vlny rovinné. Lze ji popsat podobným výrazem, jako vlnu rovinnou, jen její komplexní amplituda je slabě modulována ve směru osy z (mění se málo amplituda i fáze). Její vlnoplochy jsou proto málo zakřiveny a světelné paprsky (definované v kapitole 10 jako normály k vlnoplochám, viz rov. (10.24) svírají malé úhly s osou z. Odpovídá to situaci paraxiálního přiblížení v geometrické optice (srov. odst. 10.2). Pro tento případ lze zjednodušit vlnovou rovnici pro komplexní amplitudy vln. Uvažujme vlnu
. Vlny, pro něž si vlnoplochy a plochy konstantní amplitudy neodpovídají, se nazývají nehomogenní.
Pozn. 4 Název "rovinné vlny" se obvykle užívá pro "homogenní rovinné vlny", které uvažujeme také zde.
Pozn. 5 Ze vztahů (1.35, 1.36) plyne, že pro nulovou hodnotu elektrického pole E je nulová i hodnota magnetického pole B, tj. obě pole jsou v postupující elektromagnetické rovinné vlně ve fázi.
Pozn. 6 Harmonickou vlnu lze ekvivalentně popsat jak funkcí sinus tak funkcí kosinus, které se liší jen fázovým posuvem. Dáváme zde přednost funkci cos.
Pozn. 7 V této poznámce použijeme komplexní reprezentaci vln, jak bude zavedena v odstavci 1.5. V optice se často setkáváme se situací, kdy postupuje v určitém směru (osa z) vlna, která se málo liší od vlny rovinné. Lze ji popsat podobným výrazem, jako vlnu rovinnou, jen její komplexní amplituda je slabě modulována ve směru osy z (mění se málo amplituda i fáze). Její vlnoplochy jsou proto málo zakřiveny a světelné paprsky (definované v kapitole 10 jako normály k vlnoplochám, viz rov. (10.24) svírají malé úhly s osou z. Odpovídá to situaci paraxiálního přiblížení v geometrické optice (srov. odst. 10.2). Pro tento případ lze zjednodušit vlnovou rovnici pro komplexní amplitudy vln. Uvažujme vlnu
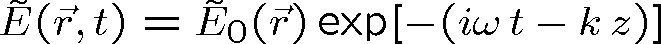 , která splňuje Helmholtzovu vlnovou rovnici (1.43). Malé změny komplexní amplitudy ve směru osy z lze kvantifikovat tak, že relativní změna amplitudy (reálná i imaginární část) se mění málo na vzdálenosti λ. Tedy
, která splňuje Helmholtzovu vlnovou rovnici (1.43). Malé změny komplexní amplitudy ve směru osy z lze kvantifikovat tak, že relativní změna amplitudy (reálná i imaginární část) se mění málo na vzdálenosti λ. Tedy
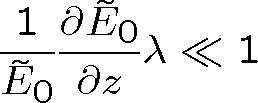 , resp. derivováním také
, resp. derivováním také
 . Dosazením pole do rov. (1.43) a uvážením
. Dosazením pole do rov. (1.43) a uvážením
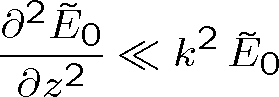 dostaneme rovnici
dostaneme rovnici
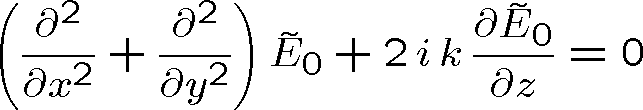 ,
což je takzvaný paraxiální tvar Helmholtzovy rovnice, který připomíná Schrödingerovu rovnici kvantové mechaniky. Řešením paraxiální Helmholtzovy rovnice jsou například gaussovské (tj. laserové) svazky o nichž se zmíníme podrobněji v kapitole 15.
Pozn. 8 Frekvence se někdy vyjadřuje, zejména ve spektroskopii, pomocí vlnočtu:
,
což je takzvaný paraxiální tvar Helmholtzovy rovnice, který připomíná Schrödingerovu rovnici kvantové mechaniky. Řešením paraxiální Helmholtzovy rovnice jsou například gaussovské (tj. laserové) svazky o nichž se zmíníme podrobněji v kapitole 15.
Pozn. 8 Frekvence se někdy vyjadřuje, zejména ve spektroskopii, pomocí vlnočtu:
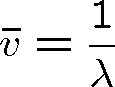 (zpravidla se vlnová délka dosazuje v cm, nejčastěji užívanou jednotkou vlnočtu je cm-1).
Pozn. 9 Je důležité si uvědomit velikosti právě zmíněných veličin pro světelné vlny. Například (ve vakuu,
(zpravidla se vlnová délka dosazuje v cm, nejčastěji užívanou jednotkou vlnočtu je cm-1).
Pozn. 9 Je důležité si uvědomit velikosti právě zmíněných veličin pro světelné vlny. Například (ve vakuu,
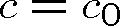 ) vlnové délce
) vlnové délce
 odpovídá
odpovídá
 ,
,
 ,
,
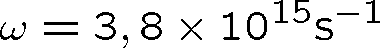 ,
,
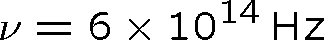 ,
,
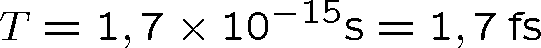 .
Pozn. 10 Intenzita světla závisí tedy nejen na velikosti amplitudy pole, ale i na indexu lomu prostředí, ve kterém se šíří. Intenzitu světla pro rovinnou vlnu můžeme vyjádřit také pomocí amplitudy magnetického pole,
.
Pozn. 10 Intenzita světla závisí tedy nejen na velikosti amplitudy pole, ale i na indexu lomu prostředí, ve kterém se šíří. Intenzitu světla pro rovinnou vlnu můžeme vyjádřit také pomocí amplitudy magnetického pole,
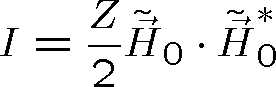 .
Pozn. 11 Výpočet Laplaceova operátoru ve sféricky symetrickém případě:
.
Pozn. 11 Výpočet Laplaceova operátoru ve sféricky symetrickém případě:
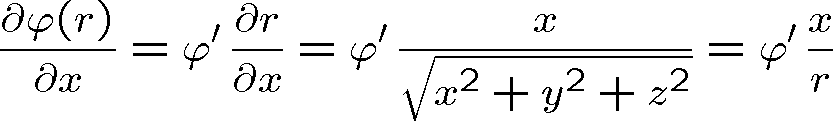
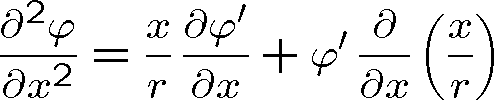 ,
,

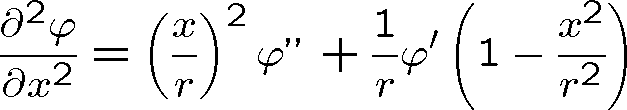 ,
a konečně
,
a konečně

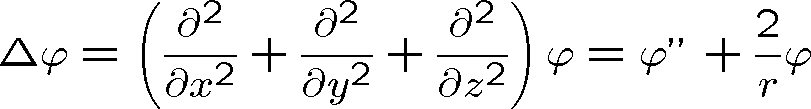 .
Pozn. 12 Vlnový vektor míří ve směru osy z, má tedy jen z-ovou komponentu, která má reálnou a imaginární složku.
Pozn. 13 Pokles intenzity světla je zde způsoben vodivostí, tedy z mikroskopického hlediska vodivostními (volnými) elektrony v kovech nebo polovodičích. K absorpci světla může ale docházet také v dielektrikách (izolantech), kde jsou jen vázané elektrony. O mikroskopickém modelu absorpce světla se zmíníme v kapitole 14. Tvar zákona (1.95) je však obecný.
Pozn. 14 Někdy se místo absorpčního koeficientu užívá optická hustota vzorku, značená obvykle OD (z angl. optical density) definovaná vztahem
.
Pozn. 12 Vlnový vektor míří ve směru osy z, má tedy jen z-ovou komponentu, která má reálnou a imaginární složku.
Pozn. 13 Pokles intenzity světla je zde způsoben vodivostí, tedy z mikroskopického hlediska vodivostními (volnými) elektrony v kovech nebo polovodičích. K absorpci světla může ale docházet také v dielektrikách (izolantech), kde jsou jen vázané elektrony. O mikroskopickém modelu absorpce světla se zmíníme v kapitole 14. Tvar zákona (1.95) je však obecný.
Pozn. 14 Někdy se místo absorpčního koeficientu užívá optická hustota vzorku, značená obvykle OD (z angl. optical density) definovaná vztahem
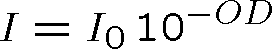 . Porovnáním s (1.95) je zřejmé, že
. Porovnáním s (1.95) je zřejmé, že
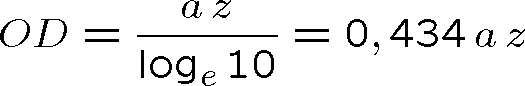 .
.
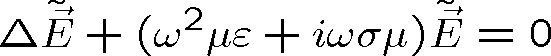
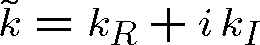
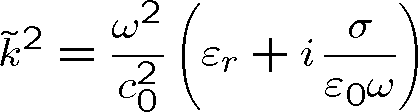
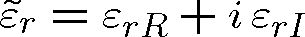
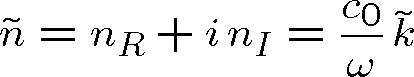
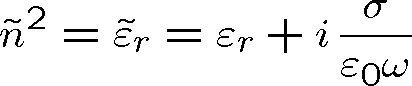
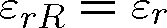 . Vyjádříme-li monochromatickou rovinnou vlnu, která se šíří ve směru osy z, pomocí komplexního vlnového vektoru12, můžeme do rov. (1.64) dosadit rov. (1.89)
. Vyjádříme-li monochromatickou rovinnou vlnu, která se šíří ve směru osy z, pomocí komplexního vlnového vektoru12, můžeme do rov. (1.64) dosadit rov. (1.89)
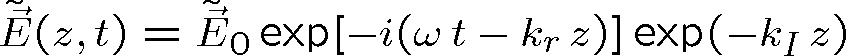
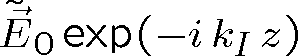 . Vyjádříme-li nyní intenzitu světla podle rov. (1.72) máme
. Vyjádříme-li nyní intenzitu světla podle rov. (1.72) máme

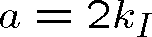
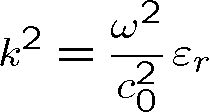 )
)
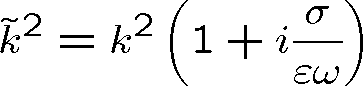
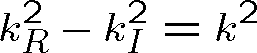
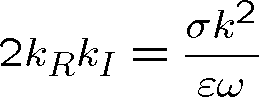
 do rov. (1.98) a získat tak kvadratickou rovnici pro
do rov. (1.98) a získat tak kvadratickou rovnici pro
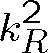 :
:
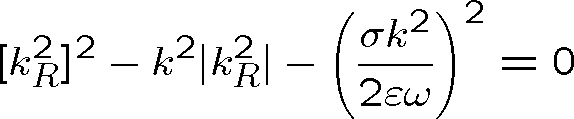
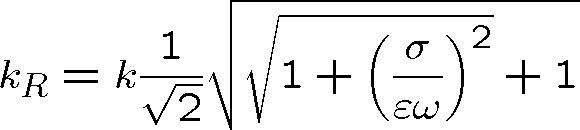
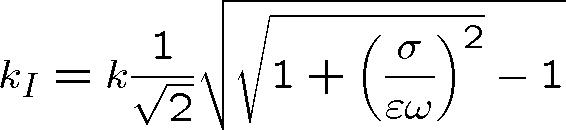
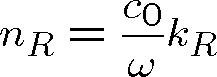 .
Pomocí rov. (1.101) tedy můžeme explicitně psát
.
Pomocí rov. (1.101) tedy můžeme explicitně psát
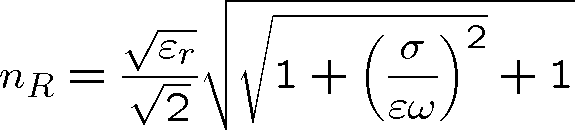
 , dostáváme z tohoto obecného vztahu obvykle používaný (1.16). Z rov. (1.96) a (1.102) můžeme vyjádřit absorpční koeficient. Velmi často je veličina
, dostáváme z tohoto obecného vztahu obvykle používaný (1.16). Z rov. (1.96) a (1.102) můžeme vyjádřit absorpční koeficient. Velmi často je veličina
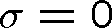 malá, takže lze s dobrou přesností aproximovat odmocninu
malá, takže lze s dobrou přesností aproximovat odmocninu
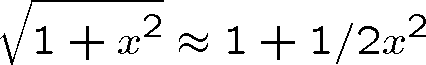 , což vede k obvykle užívanému výrazu pro absorpční koeficient
, což vede k obvykle užívanému výrazu pro absorpční koeficient
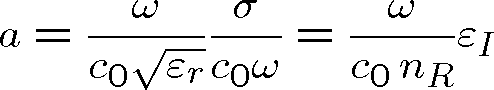
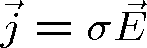 ) vodič rovnice kontinuity proudu,
) vodič rovnice kontinuity proudu,
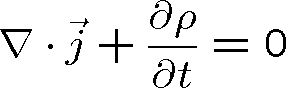 , a rov. (1.3), dostáváme pro hustotu náboje diferenciální rovnici
, a rov. (1.3), dostáváme pro hustotu náboje diferenciální rovnici
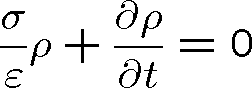 , která má řešení odpovídající exponenciálnímu poklesu:
, která má řešení odpovídající exponenciálnímu poklesu:
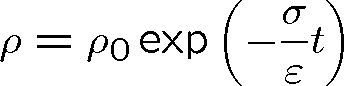 .
Pozn. 3 Je-li například vlna popsána funkcí
.
Pozn. 3 Je-li například vlna popsána funkcí
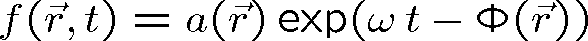 , je plocha konstantní amplitudy dána rovnicí
, je plocha konstantní amplitudy dána rovnicí
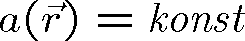 , vlnoplocha rovnicí
, vlnoplocha rovnicí
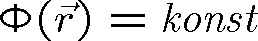 . Vlny, pro něž si vlnoplochy a plochy konstantní amplitudy neodpovídají, se nazývají nehomogenní.
Pozn. 4 Název "rovinné vlny" se obvykle užívá pro "homogenní rovinné vlny", které uvažujeme také zde.
Pozn. 5 Ze vztahů (1.35, 1.36) plyne, že pro nulovou hodnotu elektrického pole E je nulová i hodnota magnetického pole B, tj. obě pole jsou v postupující elektromagnetické rovinné vlně ve fázi.
Pozn. 6 Harmonickou vlnu lze ekvivalentně popsat jak funkcí sinus tak funkcí kosinus, které se liší jen fázovým posuvem. Dáváme zde přednost funkci cos.
Pozn. 7 V této poznámce použijeme komplexní reprezentaci vln, jak bude zavedena v odstavci 1.5. V optice se často setkáváme se situací, kdy postupuje v určitém směru (osa z) vlna, která se málo liší od vlny rovinné. Lze ji popsat podobným výrazem, jako vlnu rovinnou, jen její komplexní amplituda je slabě modulována ve směru osy z (mění se málo amplituda i fáze). Její vlnoplochy jsou proto málo zakřiveny a světelné paprsky (definované v kapitole 10 jako normály k vlnoplochám, viz rov. (10.24) svírají malé úhly s osou z. Odpovídá to situaci paraxiálního přiblížení v geometrické optice (srov. odst. 10.2). Pro tento případ lze zjednodušit vlnovou rovnici pro komplexní amplitudy vln. Uvažujme vlnu
. Vlny, pro něž si vlnoplochy a plochy konstantní amplitudy neodpovídají, se nazývají nehomogenní.
Pozn. 4 Název "rovinné vlny" se obvykle užívá pro "homogenní rovinné vlny", které uvažujeme také zde.
Pozn. 5 Ze vztahů (1.35, 1.36) plyne, že pro nulovou hodnotu elektrického pole E je nulová i hodnota magnetického pole B, tj. obě pole jsou v postupující elektromagnetické rovinné vlně ve fázi.
Pozn. 6 Harmonickou vlnu lze ekvivalentně popsat jak funkcí sinus tak funkcí kosinus, které se liší jen fázovým posuvem. Dáváme zde přednost funkci cos.
Pozn. 7 V této poznámce použijeme komplexní reprezentaci vln, jak bude zavedena v odstavci 1.5. V optice se často setkáváme se situací, kdy postupuje v určitém směru (osa z) vlna, která se málo liší od vlny rovinné. Lze ji popsat podobným výrazem, jako vlnu rovinnou, jen její komplexní amplituda je slabě modulována ve směru osy z (mění se málo amplituda i fáze). Její vlnoplochy jsou proto málo zakřiveny a světelné paprsky (definované v kapitole 10 jako normály k vlnoplochám, viz rov. (10.24) svírají malé úhly s osou z. Odpovídá to situaci paraxiálního přiblížení v geometrické optice (srov. odst. 10.2). Pro tento případ lze zjednodušit vlnovou rovnici pro komplexní amplitudy vln. Uvažujme vlnu
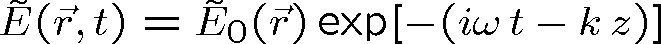 , která splňuje Helmholtzovu vlnovou rovnici (1.43). Malé změny komplexní amplitudy ve směru osy z lze kvantifikovat tak, že relativní změna amplitudy (reálná i imaginární část) se mění málo na vzdálenosti λ. Tedy
, která splňuje Helmholtzovu vlnovou rovnici (1.43). Malé změny komplexní amplitudy ve směru osy z lze kvantifikovat tak, že relativní změna amplitudy (reálná i imaginární část) se mění málo na vzdálenosti λ. Tedy
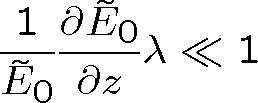 , resp. derivováním také
, resp. derivováním také
 . Dosazením pole do rov. (1.43) a uvážením
. Dosazením pole do rov. (1.43) a uvážením
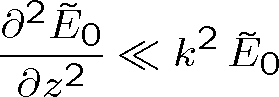 dostaneme rovnici
dostaneme rovnici
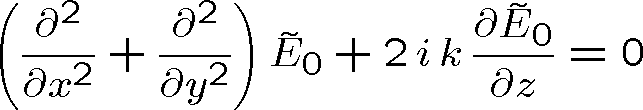 ,
což je takzvaný paraxiální tvar Helmholtzovy rovnice, který připomíná Schrödingerovu rovnici kvantové mechaniky. Řešením paraxiální Helmholtzovy rovnice jsou například gaussovské (tj. laserové) svazky o nichž se zmíníme podrobněji v kapitole 15.
Pozn. 8 Frekvence se někdy vyjadřuje, zejména ve spektroskopii, pomocí vlnočtu:
,
což je takzvaný paraxiální tvar Helmholtzovy rovnice, který připomíná Schrödingerovu rovnici kvantové mechaniky. Řešením paraxiální Helmholtzovy rovnice jsou například gaussovské (tj. laserové) svazky o nichž se zmíníme podrobněji v kapitole 15.
Pozn. 8 Frekvence se někdy vyjadřuje, zejména ve spektroskopii, pomocí vlnočtu:
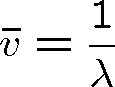 (zpravidla se vlnová délka dosazuje v cm, nejčastěji užívanou jednotkou vlnočtu je cm-1).
Pozn. 9 Je důležité si uvědomit velikosti právě zmíněných veličin pro světelné vlny. Například (ve vakuu,
(zpravidla se vlnová délka dosazuje v cm, nejčastěji užívanou jednotkou vlnočtu je cm-1).
Pozn. 9 Je důležité si uvědomit velikosti právě zmíněných veličin pro světelné vlny. Například (ve vakuu,
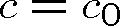 ) vlnové délce
) vlnové délce
 odpovídá
odpovídá
 ,
,
 ,
,
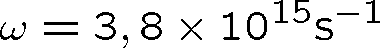 ,
,
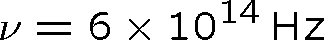 ,
,
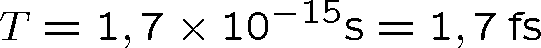 .
Pozn. 10 Intenzita světla závisí tedy nejen na velikosti amplitudy pole, ale i na indexu lomu prostředí, ve kterém se šíří. Intenzitu světla pro rovinnou vlnu můžeme vyjádřit také pomocí amplitudy magnetického pole,
.
Pozn. 10 Intenzita světla závisí tedy nejen na velikosti amplitudy pole, ale i na indexu lomu prostředí, ve kterém se šíří. Intenzitu světla pro rovinnou vlnu můžeme vyjádřit také pomocí amplitudy magnetického pole,
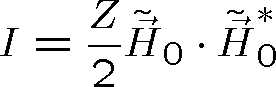 .
Pozn. 11 Výpočet Laplaceova operátoru ve sféricky symetrickém případě:
.
Pozn. 11 Výpočet Laplaceova operátoru ve sféricky symetrickém případě:
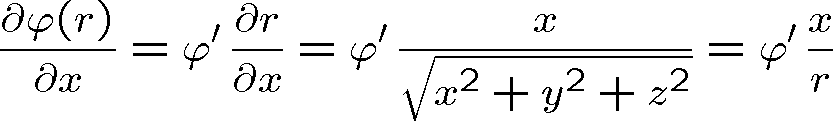
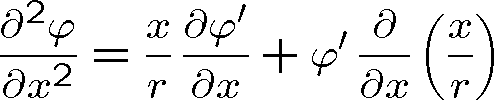 ,
,

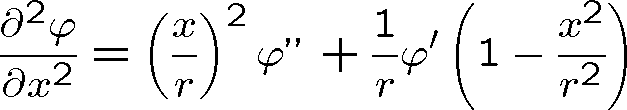 ,
a konečně
,
a konečně

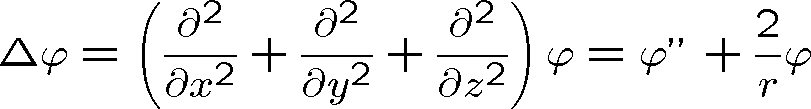 .
Pozn. 12 Vlnový vektor míří ve směru osy z, má tedy jen z-ovou komponentu, která má reálnou a imaginární složku.
Pozn. 13 Pokles intenzity světla je zde způsoben vodivostí, tedy z mikroskopického hlediska vodivostními (volnými) elektrony v kovech nebo polovodičích. K absorpci světla může ale docházet také v dielektrikách (izolantech), kde jsou jen vázané elektrony. O mikroskopickém modelu absorpce světla se zmíníme v kapitole 14. Tvar zákona (1.95) je však obecný.
Pozn. 14 Někdy se místo absorpčního koeficientu užívá optická hustota vzorku, značená obvykle OD (z angl. optical density) definovaná vztahem
.
Pozn. 12 Vlnový vektor míří ve směru osy z, má tedy jen z-ovou komponentu, která má reálnou a imaginární složku.
Pozn. 13 Pokles intenzity světla je zde způsoben vodivostí, tedy z mikroskopického hlediska vodivostními (volnými) elektrony v kovech nebo polovodičích. K absorpci světla může ale docházet také v dielektrikách (izolantech), kde jsou jen vázané elektrony. O mikroskopickém modelu absorpce světla se zmíníme v kapitole 14. Tvar zákona (1.95) je však obecný.
Pozn. 14 Někdy se místo absorpčního koeficientu užívá optická hustota vzorku, značená obvykle OD (z angl. optical density) definovaná vztahem
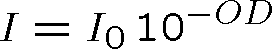 . Porovnáním s (1.95) je zřejmé, že
. Porovnáním s (1.95) je zřejmé, že
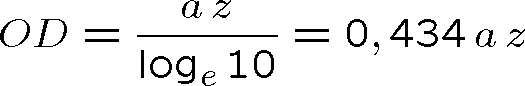 .
.