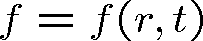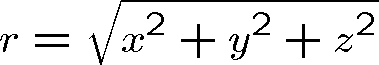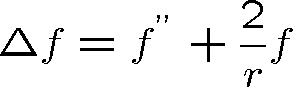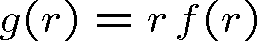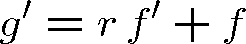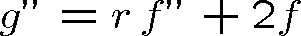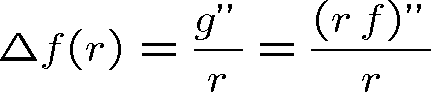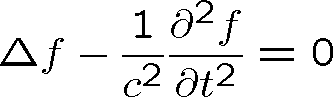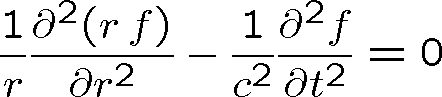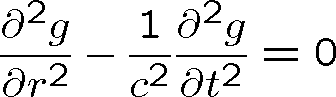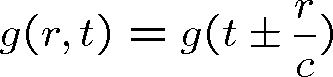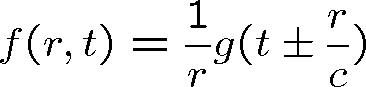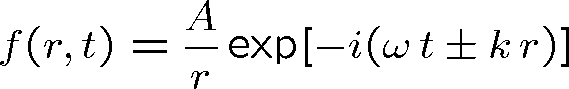1.7 Kulové vlny

Dalším důležitým řešením vlnové rovnice jsou kulové vlny, tedy vlny, jejichž vlnoplochy jsou kulové a které vycházejí nebo se sbíhají do středu (například počátku souřadného systému) jak je znázorněno na obr. 1.6. Budeme tedy uvažovat vlnu popsanou skalární funkcí, která závisí na čase t a na vzdálenosti r od počátku (skalární sféricky symetrická vlna) :

Obr. 1.6 Kulová vlna

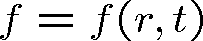(1.75)

Vzdálenost r je zřejmě rovna

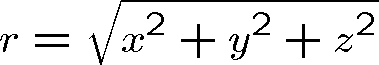(1.76)

Laplaceův operátor ve vlnové rovnici lze vyjádřit¹¹ pomocí derivace podle r (značíme ji čárkou)

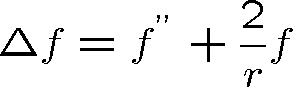(1.77)

Pravou stranu této rovnice můžeme vyjádřit vhodně pomocí další sféricky symetrické funkce

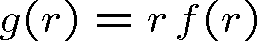(1.78)

Skutečně,

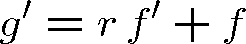(1.79)

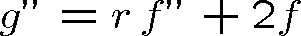(1.80)

Platí tedy

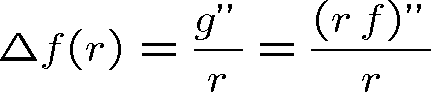(1.81)

Vlnovou rovnici

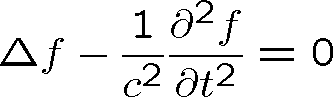(1.82)

můžeme tedy psát

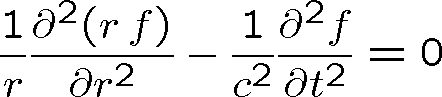(1.83)

respektive po vynásobení r

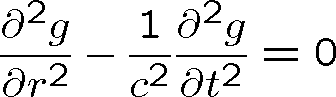(1.84)

To je ovšem jednorozměrná vlnová rovnice (srov. rov. (1.17)) jejímž řešením je (srov. rov. (1.25))

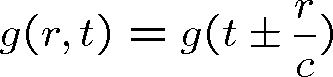(1.85)

Podle rov. (1.78) dostáváme sférickou vlnu

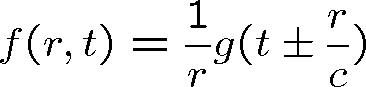(1.86)

Pro harmonickou vlnu tak máme například

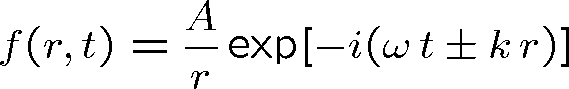(1.87)

Znaménko + odpovídá sbíhavé vlně (která se sbíhá do počátku), znaménko - vlně rozbíhavé. A je amplituda. Kulová vlna není dobře definována v bodě r = 0.

Neuvažovali jsme zde vektorový charakter pole, protože není dobře slučitelný s uvedenou sférickou symetrií. Neexistuje například lineárně polarizovaná vlna s konstantní amplitudou na celé kulové vlnoploše. V reálných případech se ale zabýváme kulovou vlnou jen v určitém prostorovém úhlu, ve kterém kulové zakřivení vlnoplochy a vektorová povaha pole nejsou ve sporu. Ve velkých vzdálenostech od bodového zdroje je možné kulovou vlnu aproximovat vlnou rovinnou. Příčně omezené je i světlo vycházející z plošných (nebo velmi vzdálených zdrojů), jehož vlnoplochy jsou rovinné. Hovoří se pak někdy o kvazirovinných vlnách, které je však možné v určité prostorové oblasti rovinnou vlnou dobře aproximovat. Složitější světlná pole je možné popsat superpozicí jednoduchých, například rovinných vln (rozvoj do rovinných vln).