Pro popis vln popsaných harmonickými funkcemi je výhodné zavést komplexní reprezentaci polí. V optice jde zejména o elektrické pole. Zavedení komplexní reprezentace ukážeme názorně na příkladu rovinné monochromatické vlny
 |
(1.59) |
 |
(1.60) |
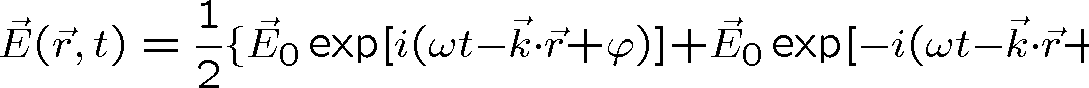 |
(1.61) |

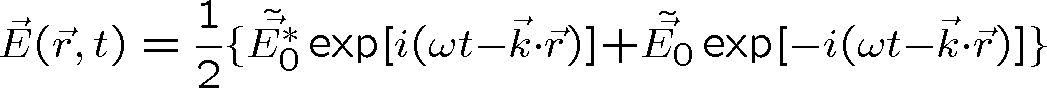 , (1.62)
kde jsme zavedli komplexní amplitudu
, (1.62)
kde jsme zavedli komplexní amplitudu
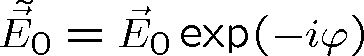 |
(1.63) |
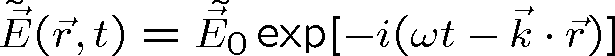 |
(1.64) |
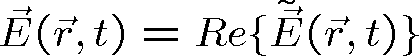 |
(1.65) |
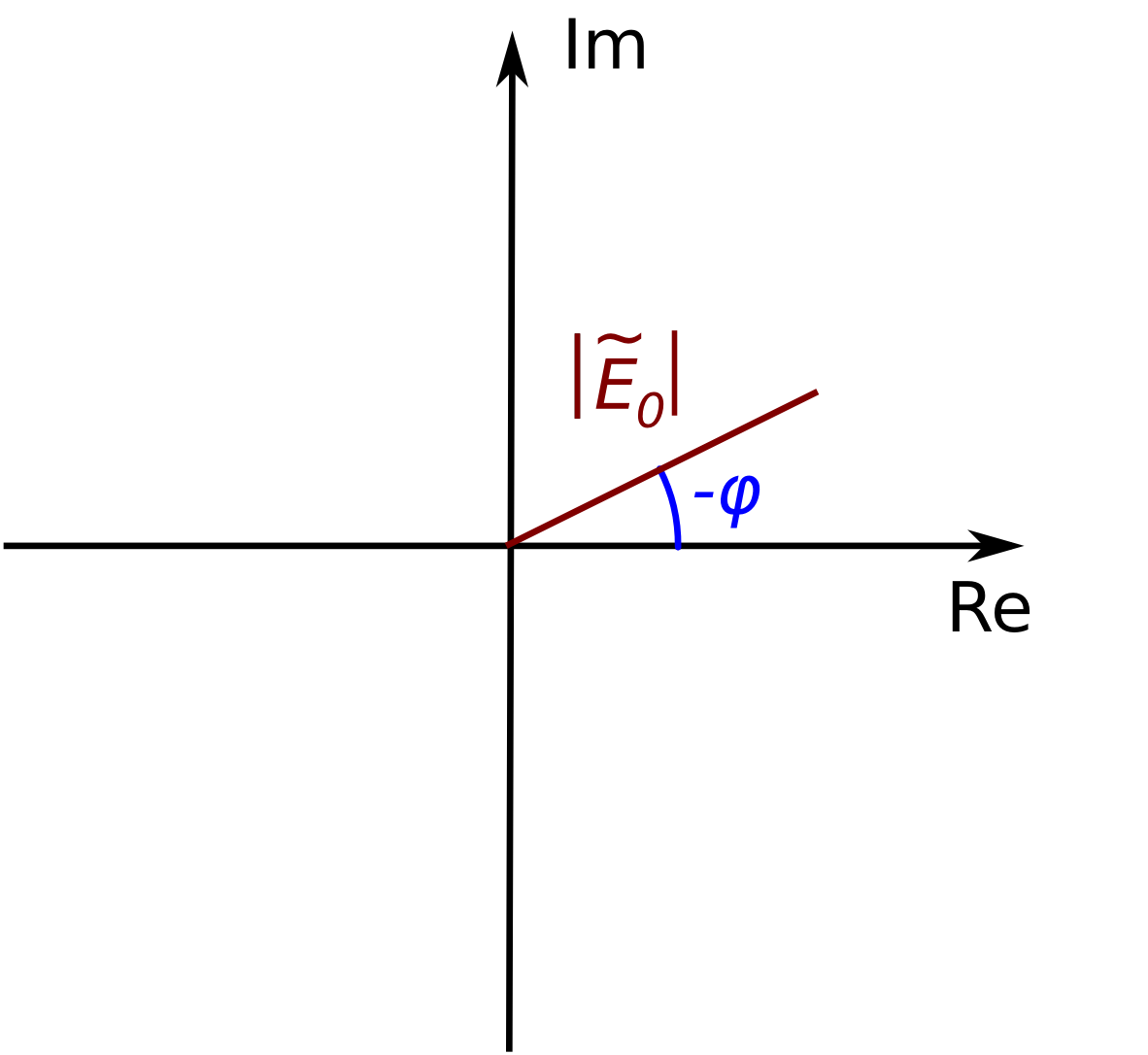
 . Je zřejmé, že součet komplexních čísel odpovídá vektorovému součtu vektorů, kterými jsou znázorněny. Skalární komplexní amplitudu proto můžeme znázornit jako na obr. 1.5, velikost vektoru odpovídá modulu komplexní amplitudy E0 , jeho úhel vůči ose
. Je zřejmé, že součet komplexních čísel odpovídá vektorovému součtu vektorů, kterými jsou znázorněny. Skalární komplexní amplitudu proto můžeme znázornit jako na obr. 1.5, velikost vektoru odpovídá modulu komplexní amplitudy E0 , jeho úhel vůči ose
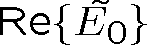 odpovídá argumentu komplexní amplitudy a je roven
odpovídá argumentu komplexní amplitudy a je roven
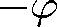 . Skládá-li se v určitém místě více vlnění stejné frekvence, která lze popsat skalárními komplexními amplitudami
. Skládá-li se v určitém místě více vlnění stejné frekvence, která lze popsat skalárními komplexními amplitudami
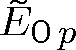 , je komplexní amplituda výsledné vlny
, je komplexní amplituda výsledné vlny
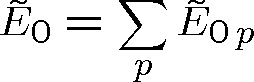 |
(1.66) |