---

---

9.7 Kapilární jevy v úzkých trubicích

Ponoříme-li velmi úzkou trubici malého vnitřního průměru (kapiláru) svisle do kapaliny v širší nádobě, pozorujeme zakřivení povrchu kapaliny v trubici a její vzestup nebo snížení vzhledem k hladině kapaliny v nádobě. U kapalin smáčej í-

* R S. de Laplace, 1749-1827, franc. matematik a fyzik

cích stěny trubice se vytvoří v trubici dutý vrchlík, který je výše než hladina okolní kapaliny, obr. 9-14a. Nastává kapilární elevace. U kapalin stěny nesmáče-jících vytvoří hladina v trubici vypuklý vrchlík, a bude níže než hladina okolní kapaliny, obr. 9-14b. Nastává kapilární deprese.

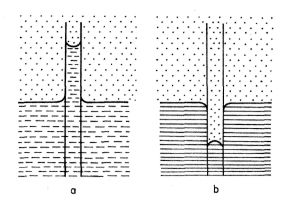Obr. 9-14

Elevační výšku h (obr. 9-15) určíme úvahou opírající se o základní rovnici hydrostatiky Podle ní musí být v kapalině, která je v tíhovém poli v rovnovážném stavu, v každém místě vodorovné roviny vedené kapalinou stejný tlak. Předpokládejme, že nad volným povrchem kapaliny je atmosférický tlak p_a, k němuž se těsně pod povrchem kapaliny přičítá kohézní tlak p_m. Povrch

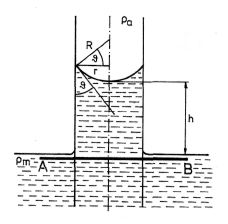Obr. 9-15

kapaliny v trubici je pod tlakem p_a zmenšeným však o tlak sloupce vzduchu výšky h, který je nad kapalinou. Tlak tohoto sloupce j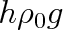e , kde 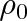je hustota vzduchu. K tlaku 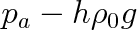se přičítá kohézní tlak p_m, který je však vlivem dutě zakřiveneého povrchu kapaliny v trubici zmenšen o kapilární tlak . Přičítá se rovněž hydrostatický tlak 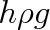sloupce kapaliny výšky h a hustoty

q v rovině proložené povrchem kapaliny v širší nádobě. Pro rovnovážný stav vztažený k této rovině lze proto napsat rovnici

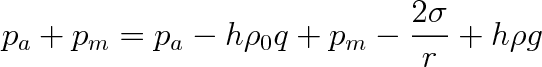(9.19)

Z ní pro elevační výšku h plyne vztah

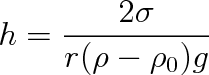(9.20)

Poloměr r křivosti vydutého menisku vyjádříme vztahem 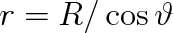(viz obr. 9-15), kde R je vnitřní poloměr trubice a 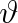krajní úhel. Dosazením r do (9.20) a uvážením toho, že 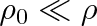, dostaneme po úpravě pro elevační výšku h vztah

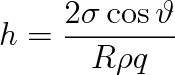(9.21)

Pro kapaliny dobře smáčející stěny trubice je 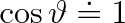, takže pro elevační výšku dobře smáčejících kapalin platí vztah

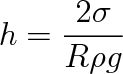(9.22)

Na základě vztahu (9.22), resp. (9.21) můžeme měřit povrchové napětí kapaliny, viz např. [3].

Jde-li o kapilární depresi, změní v rovnici (9.19) hydrostatické tlaky 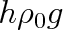a svá znaménka. Protože meniskus je při depresi vydutý, je kapilární tlak 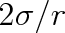kladný. Z tohoto důvodu vyjde pro snížení h hladiny kapaliny nesmáčející stěny tentýž vztah jako pro elevaci.

---

---