 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Je-li povrch kapaliny zakřivený, působí povrchová vrstva na kapalinu jinou silou, než je tomu u rovinného povrchu. Abychom vysvětlili toto experimentální zjištění vlastnostmi povrchové vrstvy, uvažujme molekulu vždy ve stejné hloubce pod povrchem rovinným, vypuklým a vydutým (obr. 9-11 a, b, c) a její sféru molekulového působení.
Obr. 9-11
Vyšrafované části sféry molekulového působení na obr. 9-11 představují část prostoru vyplněného molekulami kapaliny, jejichž vliv není kompenzován molekulami plynu (vzduchu a syté páry, které jsou v prostoru stejného objemu nad hladinou kapaliny). Je vidět, že v případě obr. 9-1lb je tento objem větší než na obr. 9-1la. Proto je výslednice molekulových sil u vypuklého povrchu větší než u rovinného. V případě obr. 9-1lc je naopak nevykompenzovaná část sféry molekulového působení menší než u rovinného povrchu. Proto je také výslednice sil menší.
Přídavný tlak pk, který vzniká vlivem zakřivení povrchu kapaliny, se nazývá kapilární tlak. Přičítá se ke kohéznímu tlaku při vypuklém povrchu a odečítá se od něj při povrchu vydutém.
Vypočítáme nejprve kapilární tlak pk v jednoduchém případě kulové kapky o poloměru r. Vyjdeme z úvahy, že práce, kterou vykonají povrchové síly při zmenšení obsahu plochy S povrchu kapky o dS, vede podle vztahu (9.7) ke zmenšení povrchové energie kapky o
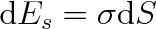. Tutéž práci lze však také vyjádřit jako práci spojenou se zmenšením objemu V kapky o hodnotu dV, při čemž platí dW = pk dV. Je tedy
 |
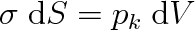(9.14) |
Protože obsah S povrchu kapky je
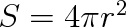a její objem
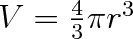, lze z předchozí rovnice dospět ke vztahu
 |
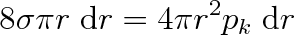z něhož pro kapilární tlak pod kulovým povrchem vyplývá vztah
 |
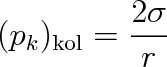(9.15) |
U kulových bublin, vytvořených např. z mýdlového roztoku, je vlivem kapilárního tlaku tlak vzduchu uvnitř větší, než je vnější tlak. Je-li vnější tlak roven atmosférickému tlaku pa a kapilární tlak vyvolaný bublinou pk, je tlak vzduchu p uvnitř bubliny roven pa + pk. Vezmeme-li v úvahu, že na rozdíl od kulové kapky má bublina dva povrchy, bude tlak pk ve srovnání se vztahem (9.15) dvojnásobný. Proto pro tlak vzduchu uvnitř kulové bubliny o poloměru r platí vztah
 |
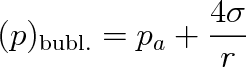(9.16) |
Předpokládejme nyní, že volný povrch kapaliny je válcový, např. mezi dvěma skleněnými deskami rovnoběžně a blízko sebe vloženými do nádoby s vodou. Je-li poměr válcové plochy r a její výška je l, je
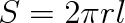a
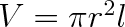. Je tedy
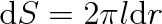a
, takže dosazením do vztahu (9.14) a úpravou dostaneme
 |
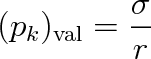(9.17) |
U povrchu obecně zakřiveného můžeme v každém jeho bodě vést dva k sobě kolmé normálové řezy tak, že poloměr křivosti r1 jednoho řezu je nejmenší a poloměr křivosti r2 druhého řezu největší z poloměrů křivosti všech normálových řezů vedených daným bodem , obr. 9-12. Pro každý element válcové plochy
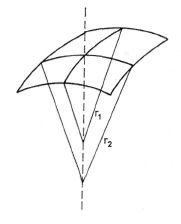Obr. 9-12
platí stejná úvaha jako u válcové plochy; tlak vyvolaný zakřivením plochy válcového tvaru o poloměru křivosti r1 je
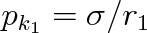, tlak vybuzený zakřivením plochy válcového tvaru o poloměru křivosti r2 je
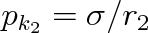. Výsledný kapilární tlak je dán součtem pk = pk1 + pk2 Je tedy
 |
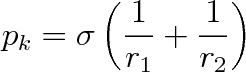(9.18) |
To je obecný Laplaceův vztah* pro kapilární tlak pod zakřiveným povrchem. Pro povrch tvaru kulové plochy je r1 = r2 = r a
, což souhlasí se vztahem (9.15).
Z výše uvedených vztahů vyplývá, že kapilární tlak je nepřímo úměrný poloměru křivosti plochy povrchu kapaliny. To lze experimentálně ukázat např. pomocí dvou mydlinových bublin spojených trubičkou s kohoutem. Vyfoukne-me-li na koncích této trubičky postupně dvě mydlinové bubliny (obr. 9-13), jednu menší, druhou větší (což lze provést pomocí trojcestného kohoutu), a pak obě bubliny pomocí kohoutu propojíme, pozorujeme, že větší bublina se zvětšuje a menší se zmenšuje. Vzduch tedy proudí z menší bubliny do větší. Uvnitř menší bubliny je větší tlak než uvnitř bubliny velké, což kvalitativně potvrzuje platnost vztahu (9.15).
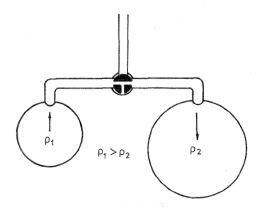Obr. 9-13
|
|
|
|
|
|
|
|
|