Nyní se budeme zabývat podrobněji vzájemným působením molekul kapalin mezi sebou a vzájemným působením těchto molekul s částicemi plynů nebo částicemi pevných látek. Důsledkem těchto interakcí je jednak existence povrchové vrstvy kapaliny, jednak jevy vznikající na rozhraní kapalina - pevné těleso.
V kapalině jsou molekuly v mnohem menších vzájemných vzdálenostech než v plynu. To znamená, že ve sféře molekulového působení (viz 1. kapitola) uvažované molekuly je dostatečný počet dalších molekul, které na ni působí přitažlivými silami. Tyto síly jsou značně veliké a vyvolávají v kapalině vnitřní
 Obr. 9-2
Obr. 9-2
neboli kohézní tlak. Jeho hodnota je úměrná veličině a ve van der Waalsově rovnici .
Abychom objasnili pojem kohézního tlaku, uvažujme nejprve molekulu A, která leží pod volným rovinným povrchem kapaliny hlouběji, než je poloměr rm (řádově 10-9 m) její sféry molekulového působení (obr. 9-2). Tato molekula působí jen na molekuly uvnitř sféry a podléhá působení jen těch molekul, které jsou uvnitř sféry. Protože uvnitř sféry je velký počet molekul (např. u vody řádově 102) prakticky rovnoměrně rozložených, ruší se navzájem interakce molekul uvnitř sféry na vybranou molekulu A a výslednice sil je rovna nule.
Podstatně jiná situace je u molekul, které jsou vzdáleny od povrchu kapaliny méně, než je poloměr rm. Sféra molekulového působení molekuly blízké povrchu proto zasahuje do prostředí nad kapalinou. Tímto prostředím jsou sytá pára uvažované kapaliny a přítomné plyny. Spodní část sféry, např. molekuly B (obr. 9-2), obsahuje tedy molekuly kapaliny, kdežto ve vrchní části jsou částice plynů. Výslednice F2 sil, jimiž působí molekuly kapaliny ve spodní části sféry na molekulu B, má směr dovnitř kapaliny kolmo k volnému povrchu kapaliny. Molekuly plynů ve vrchní části sféry působí na molekulu B výslednou silou F1, jež je rovněž kolmá k volnému povrchu, má však směr ven z kapaliny. Protože hustota molekul v kapalině je zpravidla větší než hustota molekul plynů nad kapalinou, je výslednice F = F1 + F2 síla kolmá k volnému povrchu kapaliny a směřuje dovnitř kapaliny.
Síla F má tím větší velikost, čím blíže je uvažovaná molekula k povrchu kapaliny. Největší hodnoty nabývá pro molekulu C, ležící na volném povrchu kapaliny (obr. 9-2).
Povrchová vrstva tedy působí na ostatní kapalinu tlakovou silou a vyvolává uvnitř kapaliny kohézní tlak (vnitřní tlak). Tento tlak nelze sice přímo změřit, lze jej však odhadnout na základě termodynamických úvah. Jeho hodnota je řádově GPa. Např. pro vodu má kohézní tlak hodnotu 2,03 GPa. Běžný atmosférický tlak nad kapalinou je řádově 0,1 MPa, takže je nepatrným příspěvkem ke kohéznímu tlaku.
Velkou hodnotou kohézního tlaku vysvětlujeme malou objemovou stlačitelnost kapalin. Je to pochopitelné, uvážíme-li, že při tak vysoké hodnotě tlaku uvnitř kapaliny nemůže vnější tlak řádově 0,1 MPa až 10 MPa vyvolat větší změnu objemu kapaliny. Velká hodnota kohézního tlaku také svědčí o velké velikosti působících sil mezi molekulami kapaliny.
S kohézním tlakem v kapalinách jsou úzce spjaty veličiny povrchové energie, povrchová síla a povrchové napětí.
Z předchozího výkladu vyplývá, že převedení molekuly z vnitřku kapaliny do její povrchové vrstvy je spojeno s vykonáním práce proti silám F molekulového působení. To však znamená, že molekuly obsažené v povrchové vrstvě mají větší vnitřní potenciální energii, než by měly uvnitř kapaliny. Tento rozdíl potenciálních energií nazýváme energie povrchové vrstvy nebo jen krátce povrchová energie Es. Je jednou ze složek vnitřní energie kapaliny.
Povrchová energie je zřejmě tím větší, čím větší je obsah volného povrchu kapaliny.
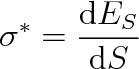 |
(9.5) |
kde
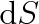 je přírůstek obsahu povrchu kapaliny a
je přírůstek obsahu povrchu kapaliny a
 konstanta úměrnosti zvaná kapilární konstanta.
konstanta úměrnosti zvaná kapilární konstanta.
takže kapilární konstanta má význam plošné hustoty energie. Jednotkou této konstanty je J . m~2.
Protože rovnovážný stav soustavy odpovídá minimu potenciální energie, má kapalina snahu zmenšit obsah svého povrchu na minimální hodnotu. O tom svědčí např. tvoření kapek rosy Kapalina v malém množství, na kterou nepůsobí vnější síly (nebo je lze zanedbat), nabývá tvaru koule, neboť ze všech geometrických těles má koule při daném objemu nejmenší obsah povrchu. Přiblížíme-li k sobě dvě kapky rtuti, spojí se v jednu, čímž se zmenší celkový obsah povrchu rtuti.
b) Uvažujme nyní případ, kdy kapku kapaliny kápneme na podložku z pevné látky. V tomto případě je úhel
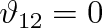 (při porovnání s obr. 9-7). Dosadíme-li tuto hodnotu do vztahu (9.9), dostaneme po jeho úpravě podmínku pro rovnovážný
(při porovnání s obr. 9-7). Dosadíme-li tuto hodnotu do vztahu (9.9), dostaneme po jeho úpravě podmínku pro rovnovážný
stav
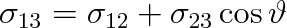 |
(9.12) |
přičemž jsme pro jednoduchost označili
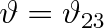 . Z této podmínky vyplývá, že
. Z této podmínky vyplývá, že
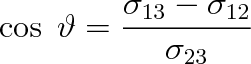 |
(9.13) |
Platí-li pro povrchová napětí, že
 a současně
a současně
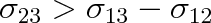 , je
, je
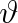 ostrý úhel a kapka má v rovnovážném stavu tvar znázorněný na obr. 9- 8a. V tomto případě říkáme, že kapalina smáčí podložku.
ostrý úhel a kapka má v rovnovážném stavu tvar znázorněný na obr. 9- 8a. V tomto případě říkáme, že kapalina smáčí podložku.
Příkladem je kapka vody na skle, rtuť na povrchu podložky z ocele, či zinku nebo zlata. Je-li
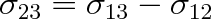 , je
, je
 . V tomto případě říkáme, že smáčení je dokonalé. Příkladem je voda, která dokonale smáčí sklo, je-li jeho povrch zbaven všech nečistot.
. V tomto případě říkáme, že smáčení je dokonalé. Příkladem je voda, která dokonale smáčí sklo, je-li jeho povrch zbaven všech nečistot.
 Obr. 9-8
Obr. 9-8
Je-li
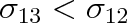 a současně
a současně
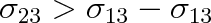 , je
, je
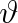 tupý úhel a kapka má v rovnovážném stavu tvar znázorněný na obr. 9-8b. Kapalina v tomto případě podložku nesmáčí. Je-li
tupý úhel a kapka má v rovnovážném stavu tvar znázorněný na obr. 9-8b. Kapalina v tomto případě podložku nesmáčí. Je-li
 , je
, je
 a mluvíme o dokonale nesmáčející kapalině. Např. rtuť nesmáčí sklo, voda nesmáčí parafinovou podložku. Přitom velmi závisí na stupni čistoty povrchu daného pevného tělesa.
a mluvíme o dokonale nesmáčející kapalině. Např. rtuť nesmáčí sklo, voda nesmáčí parafinovou podložku. Přitom velmi závisí na stupni čistoty povrchu daného pevného tělesa.
c) Předchozí poznatky lze použít také pro případ, když nalijeme kapalinu do nádoby. Pak se u vnitřní stěny nádoby stýkají tři výše uvažované prostředí: stěna z pevné látky (1), kapalina (2) a vzduch či sytá pára kapaliny (3), obr. 9-9. Příslušná povrchová napětí označme
 ,
,
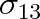 a
a
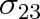 . Tato napětí nejsou obecně v rovnováze.
. Tato napětí nejsou obecně v rovnováze.
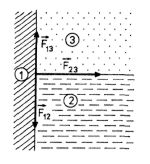 Obr. 9-9
Obr. 9-9
Je-li
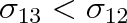 , jsou částice u stěny nádoby taženy směrem dolů. V rovnovážném stavu kapalina svírá se stěnou nádoby tupý úhel
, jsou částice u stěny nádoby taženy směrem dolů. V rovnovážném stavu kapalina svírá se stěnou nádoby tupý úhel
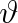 (obr. 9-10a). Pro jeho velikost opět platí vztah (9.13). V tomto případě kapalina nesmáčí stěnu, její volný povrch u stěny je vypuklý (konvexní). Např. tento povrch vytvoří rtuť při skleněné stěně a
(obr. 9-10a). Pro jeho velikost opět platí vztah (9.13). V tomto případě kapalina nesmáčí stěnu, její volný povrch u stěny je vypuklý (konvexní). Např. tento povrch vytvoří rtuť při skleněné stěně a
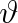 = 128°. Stejný úhel vznikne i u kapky rtuti na skleněné desce.
= 128°. Stejný úhel vznikne i u kapky rtuti na skleněné desce.
Je-li
 , posunou se částice kapaliny u stěny nádoby směrem vzhůru a povrch kapaliny u stěn svírá se stěnou ostrý úhel
, posunou se částice kapaliny u stěny nádoby směrem vzhůru a povrch kapaliny u stěn svírá se stěnou ostrý úhel
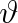 (obr. 9-10b). Pro jeho velikost platí vztah (9.13). V tomto případě je volný povrch kapaliny u stěny dutý (konkávní), kapalina smáčí stěnu. Např. voda smáčí sklo, je-li jeho povrch čistý. Pro vodu, sklo a vzduch je
(obr. 9-10b). Pro jeho velikost platí vztah (9.13). V tomto případě je volný povrch kapaliny u stěny dutý (konkávní), kapalina smáčí stěnu. Např. voda smáčí sklo, je-li jeho povrch čistý. Pro vodu, sklo a vzduch je
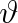 = 8°. Tento úhel je také u kapky vody na skle.
Jeho velikost závisí jen na jakosti tří prostředí, která se stýkají, a má pro tato prostředí vždy stejnou hodnotu, ať je tvar stěny jakýkoliv.
= 8°. Tento úhel je také u kapky vody na skle.
Jeho velikost závisí jen na jakosti tří prostředí, která se stýkají, a má pro tato prostředí vždy stejnou hodnotu, ať je tvar stěny jakýkoliv.
 Obr. 9-10
Obr. 9-10