 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Přidržíme se toho postupu, který použil J. C. Maxwell v roce 1860. Vycházel ze dvou základních předpokladů. Budeme-li s nimi souhlasit, je odvození poměrně snadné. Prvý je předpoklad, že pravděpodobnosti výskytu jednotlivých složek rychlosti jsou vzájemně nezávislé, druhý, že pravděpodobnost velikosti rychlosti je nezávislá na směru pohybu molekuly.
Nejprve k druhému předpokladu. Kdyby velikost rychlosti byla závislá na směru, musel by některý směr být význačný tím, že v něm převládají molekuly např. s většími rychlostmi než je průměrná rychlost. Plyn by tímto směrem proudil rychleji, než v ostatních směrech. To však u plynu v tepelné rovnováze nebylo pozorováno, a proto neexistuje důvod, proč by některý směr měl být preferován. K prvému předpokladu lze mít výhradu; bude-li jedna složka rychlosti podstatně větší, než je průměrná rychlost, mohly by být zbývající složky malé, aby celková rychlost
se blížila k průměrné hodnotě. Oprávněnost této námitky však nelze dokázat, nemáme žádné omezení shora pro velikost rychlosti jedné vybrané částice, neboť tato rychlost může být libovolná. Při odvození hustoty pravděpodobnosti se bez prvého Maxwellova předpokladu obešel L. Boltzmann roku 1896. Toto odvození je však komplikovanější. Z kvantové mechaniky, kterou Maxwell pochopitelně nemohl používat, vyplývá tento předpoklad téměř automaticky.
Jsou-li splněny oba předpoklady, můžeme psát pro hustotu pravděpodobnosti
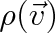, že rychlost
bude mít složky v intervalech (vx, vx + dvx), (vy , vy + dvy), (vz,vz + dvz)
 |
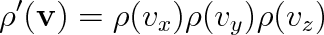(5.15) |
 |
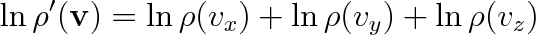Parciální derivace tohoto výrazu podle některé ze složek rychlosti, např. vx, bude rovna
 |
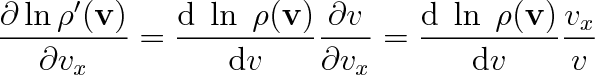protože
 |
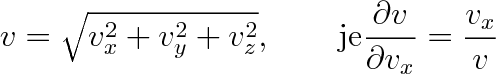Obdobné vztahy platí i pro parciální derivace podle ostatních složek, takže
 |
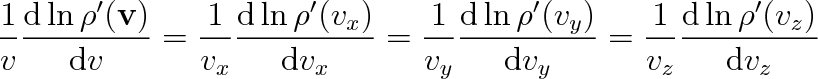Složky rychlosti jsou vzájemně nezávislé, proto tyto vztahy mohou platit pouze tehdy, jestliže každý z výrazů je nezávislý na příslušné proměnné. Musí tedy být rovny
stejné konstantě, kterou z formálních důvodů označíme -
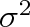. Označíme-li libovolně vybranou složku rychlosti symbolem u, pak bude platit
 |
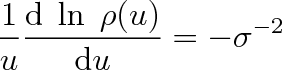(5.16) |
Po separaci proměnných můžeme integrovat
 |
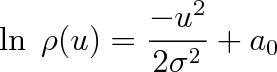a po úpravě
 |
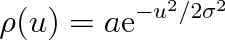(5.17) |
Veličina a je integrační konstanta, kterou můžeme určit z normovací podmínky (5.5a), neboť ji musí hustota pravděpodobnosti splňovat:
 |
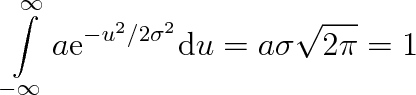Tento integrál vypočítáme následovně. Provedeme substituci
, respektive
, a budeme počítat integrál
 |
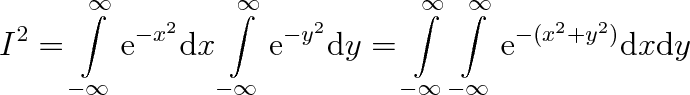To je dvojný integrál přes celou rovinu. Použijeme-li polárních souřadnic, dostaneme
 |
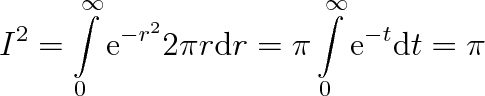takže
 |
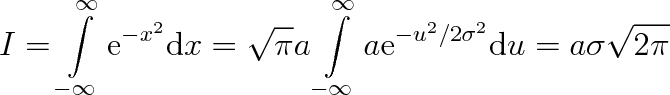Výpočet nás dovedl k závěru, že hustota pravděpodobnosti kterékoliv ze složek rychlosti má vždy tvar
 |
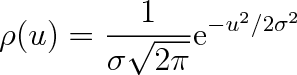(5.18) |
Tato funkce má
tvar normálního rozdělení
, střední hodnota je nulová a rozděleni má rozptyl
.
|
|
|
|
|
|
|
|
|
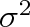