Jako ukázku použití statistické metody odvodíme výraz pro pravděpodobnost, že z celkového počtu TV molekul v nádobě o objemu V je n molekul v části nádoby o objemu
 . Uvažujeme ideální plyn, který je v tepelné rovnováze, a zanedbáme působení tíhového pole. Jeho vlivu se budeme
. Uvažujeme ideální plyn, který je v tepelné rovnováze, a zanedbáme působení tíhového pole. Jeho vlivu se budeme
věnovat v článku 5.11. Molekuly pokládáme za rozlišitelné, a můžeme je proto očíslovat. Pravděpodobnost, že prvou molekulu vložíme do zvoleného objemu
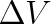 je zřejmě
je zřejmě
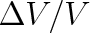 . Protože pravděpodobnost výskytu jedné molekuly není závislá na vložení druhé, bude pravděpodobnost, že v části o objemu
. Protože pravděpodobnost výskytu jedné molekuly není závislá na vložení druhé, bude pravděpodobnost, že v části o objemu
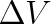 je prvých n molekul, rovna
je prvých n molekul, rovna
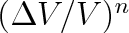 . Zbývajících (N - n) molekul musí být v objemu
. Zbývajících (N - n) molekul musí být v objemu
 . Příslušná pravděpodobnost je
. Příslušná pravděpodobnost je
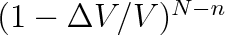 . Obě pravděpodobnosti jsou vzájemně nezávislé, takže výraz
. Obě pravděpodobnosti jsou vzájemně nezávislé, takže výraz
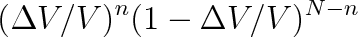 |
představuje pravděpodobnost, že v části nádoby o objemu
 je právě jen prvých n molekul. Toto tvrzení nevyjadřuje jediný způsob, jak umístit do uvažované části nádoby n molekul. Nezáleží-li na tom, kterých n molekul je v tomto objemu, musíme předchozí výraz vynásobit kombinačním číslem, které udává počet n-tic, jež lze utvořit z N částic. Tento kombinační faktor je roven
je právě jen prvých n molekul. Toto tvrzení nevyjadřuje jediný způsob, jak umístit do uvažované části nádoby n molekul. Nezáleží-li na tom, kterých n molekul je v tomto objemu, musíme předchozí výraz vynásobit kombinačním číslem, které udává počet n-tic, jež lze utvořit z N částic. Tento kombinační faktor je roven
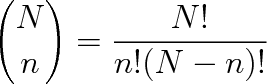 |
Jako prvou můžeme z N částic vybrat částici N způsoby, druhou (N - 1), až pro výběr poslední nám zbývá jediná možnost. Výraz N! v čitateli proto udává, kolika způsoby můžeme očíslovat N částic. Jelikož nezáleží na očíslování částic v každé z částí nádoby, musíme vydělit N! počtem permutací n! a (N - n)N!.
Pro pravděpodobnost, že v části nádoby bude n a ve zbytku nádoby (N - n) molekul, dostáváme
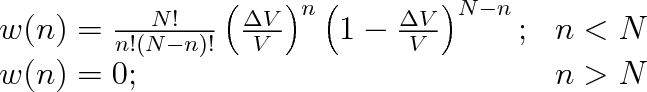 |
(5.9) |
V matematické statistice se tento výraz nazývá binomickým rozdělením. Název pochází ze skutečnosti, že výraz (5.9) je n-tým členem rozvoje výrazu
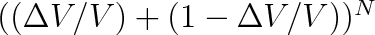 . Z toho bezprostředně vyplývá, že
. Z toho bezprostředně vyplývá, že
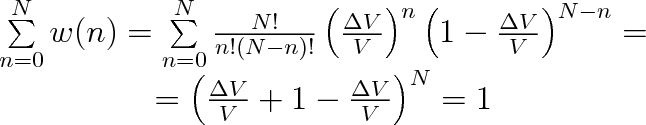 |
což je normovací podmínka, kterou musí splňovat každé rozdělení.
Střední hodnotu počtu částic v prostoru o objemu
 můžeme určit podle vztahu (5.7a). Po dosazení z rovnice (5.9) platí
můžeme určit podle vztahu (5.7a). Po dosazení z rovnice (5.9) platí
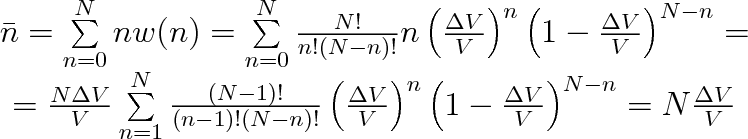 |
(5.10) |
Protože N - n = (N - 1) - (n - 1), představuje poslední suma binomický rozvoj výrazu
 . Výsledek, ke kterému jsme došli, není nijak překvapivý. Mohli jsme
. Výsledek, ke kterému jsme došli, není nijak překvapivý. Mohli jsme
k němu dojít rychleji úsudkem vycházejícím z představy, že žádné místo v nádobě není preferováno. Průměrný počet částic ve vybrané části nádoby musí být potom roven součinu hustoty částic NV = N/V a vybraného objemu
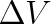 , což je výsledek, ke kterému jsme došli ve výrazu (5.10).
, což je výsledek, ke kterému jsme došli ve výrazu (5.10).
Ve vybraném prostoru o objemu
 však nebude vždy právě n molekul. Molekuly jsou v neustálém pohybu, některé zvolenou část nádoby opouští, jiné do ní vletují. Počet molekul se bude proto měnit, ovšem tak, že průměrná hodnota počtu molekul za delší časový interval bude
však nebude vždy právě n molekul. Molekuly jsou v neustálém pohybu, některé zvolenou část nádoby opouští, jiné do ní vletují. Počet molekul se bude proto měnit, ovšem tak, že průměrná hodnota počtu molekul za delší časový interval bude
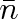 . Okamžité hodnoty mohou být jak větší, tak i menší než střední hodnota. Mluvíme o fluktuaci v počtu částic ve vybrané části prostoru.
. Okamžité hodnoty mohou být jak větší, tak i menší než střední hodnota. Mluvíme o fluktuaci v počtu částic ve vybrané části prostoru.
Nyní je na místě otázka, jak tyto fluktuace kvantitativně popsat. Nelze to provést stanovením střední hodnoty okamžitých hodnot počtu částic, neboť
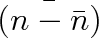 je vždy rovno nule. V matematické statistice se charakterizuje fluktuace rozptylem
je vždy rovno nule. V matematické statistice se charakterizuje fluktuace rozptylem
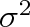 , který jsme zavedli vztahem (5.8). Abychom veličinu
, který jsme zavedli vztahem (5.8). Abychom veličinu
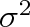 určili, musíme spočítat střední hodnotu z druhých mocnin počtu částic v prostoru o objemu A V. Dosadíme-li do vztahu (5.7a) za xi hodnoty n2 a pravděpodobnost wi označíme w(n), dostaneme postupnými úpravami
určili, musíme spočítat střední hodnotu z druhých mocnin počtu částic v prostoru o objemu A V. Dosadíme-li do vztahu (5.7a) za xi hodnoty n2 a pravděpodobnost wi označíme w(n), dostaneme postupnými úpravami
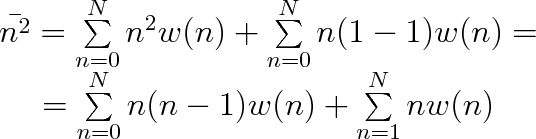 |
Druhý člen v posledním výrazu je střední hodnota počtu částic n. Prvý člen upravíme po dosazení za w(n) ze vztahu (5.9) obdobně jako vztah (5.10). Platí totiž
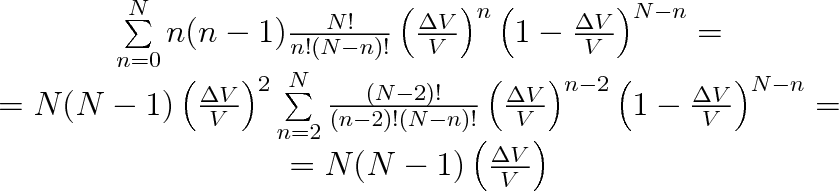 |
Poslední suma je opět rovna jedné, o čemž se přesvědčíme, zavedeme-li nový sčítací index s = n - 2. Součet je pak roven
 . Veličina
. Veličina
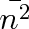 je proto rovna
je proto rovna
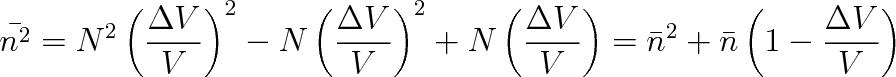 |
Rozptyl už určíme snadno ze vztahu
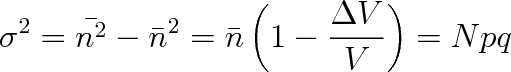 |
(5.11) |
Zápis
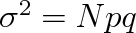 je běžným v matematické statistice, p znamená pravděpodobnost, že dostaneme pozitivní výsledek (molekula se bude nacházet v prostoru o objemu
je běžným v matematické statistice, p znamená pravděpodobnost, že dostaneme pozitivní výsledek (molekula se bude nacházet v prostoru o objemu
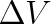 ,
,
 ), q je pravděpodobnost negativniho výsledku q = (1 - p), tj. molekula bude ve zbytku nádoby,
), q je pravděpodobnost negativniho výsledku q = (1 - p), tj. molekula bude ve zbytku nádoby,
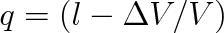 . Střední kvadratická fluktuace (rozptyl) molekul v celé nádobě je roven nule, neboť pro
. Střední kvadratická fluktuace (rozptyl) molekul v celé nádobě je roven nule, neboť pro
 je
je
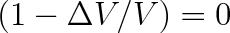 . Je to matematickým vyjádřením skutečnosti, že v uzavřené nádobě se počet částic nemění. Pro
. Je to matematickým vyjádřením skutečnosti, že v uzavřené nádobě se počet částic nemění. Pro
 můžeme člen
můžeme člen
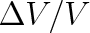 ve výrazu (5.11) zanedbat vůči jedné. Rozptyl pak bude
ve výrazu (5.11) zanedbat vůči jedné. Rozptyl pak bude
téměř roven střednímu počtu částic v prostoru o objemu
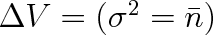 . Vezměme si konkrétní příklad: Uvažujme plyn o látkovém množství 1 mol, tlaku 0,1 MPa a teplotě 273 K. Jeho molární objem Vm bude přibližně 0,0224 m3 a plyn bude obsahovat N = {NA}
. Vezměme si konkrétní příklad: Uvažujme plyn o látkovém množství 1 mol, tlaku 0,1 MPa a teplotě 273 K. Jeho molární objem Vm bude přibližně 0,0224 m3 a plyn bude obsahovat N = {NA}
 6,02 . 1023 molekul. V prostoru o objemu 1 mm3 je v průměru {NA}
6,02 . 1023 molekul. V prostoru o objemu 1 mm3 je v průměru {NA}
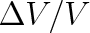
 6 . 1023 10-9/2 . 102
6 . 1023 10-9/2 . 102
 3 . 1016 molekul. Tato hodnota udává pro
3 . 1016 molekul. Tato hodnota udává pro
 i rozptyl.
i rozptyl.
Rozptyl
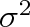 je mírou druhé mocniny odchylek. Odmocnina z něho je mírou absolutní odchylky. Veličina
je mírou druhé mocniny odchylek. Odmocnina z něho je mírou absolutní odchylky. Veličina
 se nazývá směrodatnou odchylkou a pro náš konkrétní příklad bude asi
se nazývá směrodatnou odchylkou a pro náš konkrétní příklad bude asi
 , což je relativně malá hodnota vůči střednímu počtu částic ve zkoumané části nádoby o objemu
, což je relativně malá hodnota vůči střednímu počtu částic ve zkoumané části nádoby o objemu
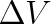 , kdy
, kdy
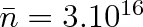 molekul. Kdyby ovšem v celé nádobě bylo pouze 109 molekul, byl by v části nádoby průměrný počet molekul pouze
molekul. Kdyby ovšem v celé nádobě bylo pouze 109 molekul, byl by v části nádoby průměrný počet molekul pouze
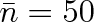 . Směrodatná odchylka by byla asi 7, což znamená asi 14 % ze střední hodnoty.
. Směrodatná odchylka by byla asi 7, což znamená asi 14 % ze střední hodnoty.
Konkrétní hodnoty jsme zde uváděli především proto, abychom si uvědomili, že za běžných podmínek je v nádobě rozumných rozměrů extrémně velký počet molekul a statisticky nalezené průměrné hodnoty se s přesností větší než je přesnost jejich experimentálního stanovení rovnají skutečným, hodnotám. Těžko můžeme objem 1 mm určit na 8 platných míst, aby neurčitost ve stanovení objemu byla menší, než směrodatná odchylka v počtu částic. Jiná je situace pro extrémně zředěný plyn. Pak střední počet částic a směrodatná odchylka mohou být veličiny srovnatelné. Fluktuace pak hrají významnou roli. Jiná je ovšem otázka, jak jejich existenci experimentálně prokázat. K tomu se vrátíme v článku 5.12.
Dejme si ještě jednou otázku. Jaká je vlastně pravděpodobnost, že v části vnitřku nádoby o objemu
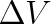 je právě tolik molekul, kolik odpovídá hodnotě
je právě tolik molekul, kolik odpovídá hodnotě
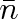 ? Tuto pravděpodobnost určuje výraz (5.9), ve kterém položíme
? Tuto pravděpodobnost určuje výraz (5.9), ve kterém položíme
 . Chceme-li pravděpodobnost w(n) určit, dostaneme se okamžitě do početních obtíží. Hodnoty faktoriálů N!, n! a (N - n)! jsou nesmírně velké. Vždyť už 50! je řádu 1064. Z obtíží nám může pomoci Moivreova-Laplaceova věta uváděná v učebnicích teorie pravděpodobnosti [7], podle které
. Chceme-li pravděpodobnost w(n) určit, dostaneme se okamžitě do početních obtíží. Hodnoty faktoriálů N!, n! a (N - n)! jsou nesmírně velké. Vždyť už 50! je řádu 1064. Z obtíží nám může pomoci Moivreova-Laplaceova věta uváděná v učebnicích teorie pravděpodobnosti [7], podle které
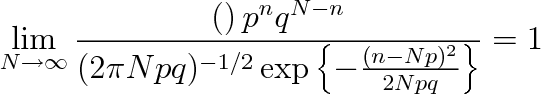 |
(5.12) |
 Obr. 5-1
Obr. 5-1
[7] Renyi, A., Teorie pravděpodobnosti, Academia Praha 1972, str. 142.
jestliže N a n rostou nade všechny meze tak, že výraz
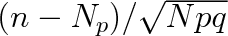 zůstává konečně velký. Konvergence je dokonce stejnoměrná. Důkaz (5.12) není jednoduchý, a proto ho zde neprovádíme. Věnujme pozornost výrazu ve jmenovateli vztahu (5.12). Ve formě, ve které je zapsán, je poměrně nepřehledný. Uvědomíme-li si, že
zůstává konečně velký. Konvergence je dokonce stejnoměrná. Důkaz (5.12) není jednoduchý, a proto ho zde neprovádíme. Věnujme pozornost výrazu ve jmenovateli vztahu (5.12). Ve formě, ve které je zapsán, je poměrně nepřehledný. Uvědomíme-li si, že
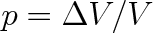 ,
,
 a že
a že
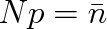 ,
,
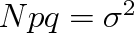 , pak můžeme psát
, pak můžeme psát
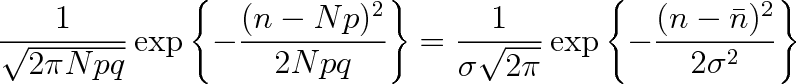 |
(5.13) |
Na pravé straně máme výraz pro normální (Gaussovo) rozdělení hustoty pravděpodobnosti se střední hodnotou
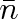 a rozptylem
a rozptylem
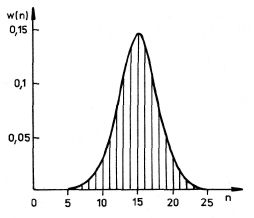
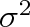 . Podle vztahu (5.12) nabývá normální rozdělení pro n rovné přirozeným číslům hodnoty rovné hodnotám binomického rozdělení. Na obrázku 5-1 jsou ve formě histogramu zakresleny hodnoty binomického rozdělení pro N = 30, p = 1/2, a spojitou křivkou normální rozdělení pro
. Podle vztahu (5.12) nabývá normální rozdělení pro n rovné přirozeným číslům hodnoty rovné hodnotám binomického rozdělení. Na obrázku 5-1 jsou ve formě histogramu zakresleny hodnoty binomického rozdělení pro N = 30, p = 1/2, a spojitou křivkou normální rozdělení pro
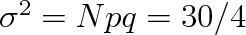 a
a
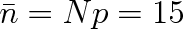 . Už při takto malém počtu částic jsou rozdíly na grafu nerozlišitelné. Při velkých hodnotách N a n, ovšem podstatně větších než 30, mizí rozdíl mezi diskrétním a spojitým průběhem obou statistických rozdělení, neboť funkční hodnoty diskrétního rozdělení budou ležet libovolně blízko sebe.
. Už při takto malém počtu částic jsou rozdíly na grafu nerozlišitelné. Při velkých hodnotách N a n, ovšem podstatně větších než 30, mizí rozdíl mezi diskrétním a spojitým průběhem obou statistických rozdělení, neboť funkční hodnoty diskrétního rozdělení budou ležet libovolně blízko sebe.
Se spojitou funkcí se podstatně lépe počítá. Snadno vysvětlíme například význam směrodatné odchylky. Spočítáme si pravděpodobnost, že výsledek náhodného pokusu se bude od střední hodnoty
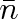 lišit nejvýše
lišit nejvýše
 . Tato pravděpodobnost je dána určitým integrálem
. Tato pravděpodobnost je dána určitým integrálem
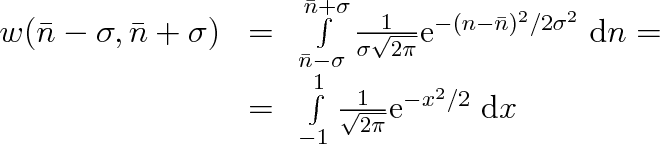 |
(5.14) |
Při poslední úpravě jsme provedli substituci
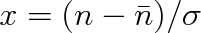 . Integrál
. Integrál
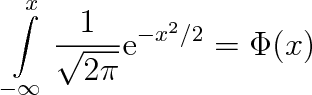 |
definuje pravděpodobnostní funkci
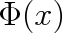 , která je tabelována a najdeme ji v matematických tabulkách. Určitý integrál (5.14) je roven rozdílu funkčních hodnot
, která je tabelována a najdeme ji v matematických tabulkách. Určitý integrál (5.14) je roven rozdílu funkčních hodnot
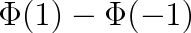 . Z tabulek se přesvědčíme, že
. Z tabulek se přesvědčíme, že
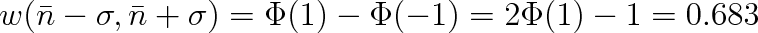 |
S pravděpodobností w = 0,683 se nebude výsledek lišit od střední hodnoty o více než směrodatnou odchylku.
Vrátíme-li se zpět k předchozímu příkladu, je pravděpodobnost, že počet molekul v 1 mm3 se bude lišit od středního počtu
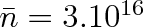 nanejvýš o
nanejvýš o
 molekul, rovna 0,683. Téměř s jistotou (w = 0,99) můžeme tvrdit, že se aktuální hodnota neliší od střední hodnoty o více než
molekul, rovna 0,683. Téměř s jistotou (w = 0,99) můžeme tvrdit, že se aktuální hodnota neliší od střední hodnoty o více než
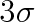 (asi o 5 . 108 molekul).
(asi o 5 . 108 molekul).
Normální rozdělení má maximum pro
 . Střední hodnota je též nejpravděpodobnější, ovšem pravděpodobnost, že je v části nádoby právě ň molekul je zpravidla velmi malá. Pro
. Střední hodnota je též nejpravděpodobnější, ovšem pravděpodobnost, že je v části nádoby právě ň molekul je zpravidla velmi malá. Pro
 bude podle Moivreovy-Laplaceovy věty pravděpodobnost w(n) přibližně rovna hodnotě normálního rozdělení s parametry Np,
bude podle Moivreovy-Laplaceovy věty pravděpodobnost w(n) přibližně rovna hodnotě normálního rozdělení s parametry Np,
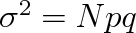 v bodě
v bodě
 .
.
Tedy
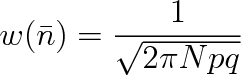 |
Pro již dřive uvažované číselné hodnoty N = 6 . 1023, p = 5 . 10-8, q = 1 bude w(n) = 2,3 . 10-9, což je hodnota srovnatelná s pravděpodobností výhry 1. pořadí ve Sportce při jediné sázce. Takováto pravděpodobnost je zanedbatelně malá a můžeme považovat za jistotu, že tento výsledek při jednom pokusu nenastane. Znamená to, že při velkém počtu molekul je pravděpodobnost dosažení určitého konkrétního výsledku, třeba i nejpravděpodobnějšího, prakticky nulová.