 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Představme si, že provádíme velkou sérii N náhodných pokusů. V této sérii nastane i-tý náhodný jev například Ni-krát. Pravděpodobností i-tého náhodného jevu nazveme výraz
 |
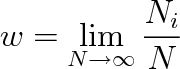(5.1) |
V řadě případů lze z charakteru prováděného pokusu předem určit tzv. apriorní pravděpodobnost.
Například pravděpodobnost
, že určitá molekula se nachází v prostoru o objemu
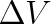z celkového objemu V, je
.
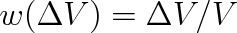U fyzikálních pokusů nemusí výsledky nabývat vždy jen diskrétních hodnot. Rychlost molekuly může z hlediska klasické nerelativistické mechaniky nabývat libovolných hodnot. Pak ovšem pravděpodobnost, že rychlost v má přesně hodnotu v0 je rovna vždy nule. Nenulová může však být pravděpodobnost
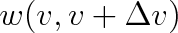, že rychlost je z intervalu
. Pravděpodobnost výskytu rychlosti z tohoto intervalu pak ovšem závisí nejen na velikosti rychlosti v, ale i na zvolené šířce intervalu
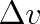. Je proto vhodné zavést hustotu pravděpodobnosti
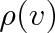vztahem
 |
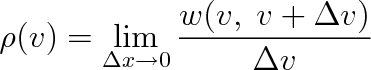(5.3) |
 |
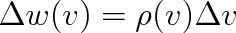(5.4) |
Zintegrujeme-li předchozí výraz přes všechny možné hodnoty veličiny v, musí být
 |
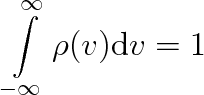(5.5a) |
neboť pravděpodobnost, že pokus skončí libovolným možným výsledkem je rovna jedné. Nabývají-li výsledky pokusu jen k diskrétních hodnot, je předchozímu vztahu ekvivalentní výraz
 |
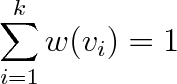(5.5b) |
Vztahy (5.5a, b) představují normovati podmínku pro hustotu pravděpodobnosti a pravděpodobnost.
Definujme si nyní nezávislost dvou náhodných pokusů. Pokusy jsou nezávislé, pokud pravděpodobnost současného výskytu i-tého výsledku prvého pokusu a j-tého výsledku druhého pokusu je rovna
 |
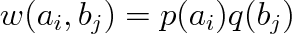(5.6) |
V běžném smyslu chápeme nezávislost jako neexistenci souvislosti mezi prováděnými pokusy, nebo je tato souvislost alespoň zanedbatelná.
Rovnici (5.6) vyjadřující pravidlo o násobení pravděpodobnosti, je možno zobecnit na N nezávislých pokusů. Pak musí být kombinace prvých dvou pokusů nezávislá na třetím pokuse atd., až kombinace prvých N - 1 pokusů je nezávislá na N-tém pokuse.
Znalost pravděpodobností jednotlivých výsledků dává sice úplný, avšak komplikovaný obraz o náhodné veličině. Je proto účelné zavést několik málo číselných charakteristik. Nejběžnější charakteristikou náhodné veličiny x je její střední hodnota
:
 |
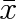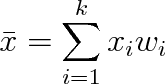(5.7a) |
 |
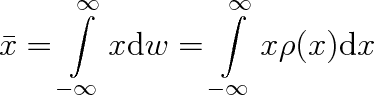(5.7b) |
Obdobně můžeme zavést i střední hodnotu libovolné funkční závislosti f(x) náhodné veličiny x, definované v intervalu (a, b). Bude platit
 |
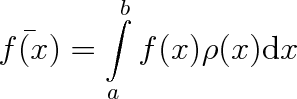(5.7c) |
Druhou důležitou charakteristikou náhodné veličiny je rozptyl
.
 |
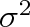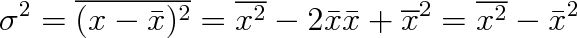(5.8) |
Rozptyl charakterizuje odchylky výsledků náhodných pokusů od střední hodnoty
.
|
|
|
|
|
|
|
|
|
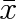