---

---

4.7 Volná energie a volná entalpie

Volná energie, zvaná také Helmholtzova energie nebo Helmholtzova funkce, je termodynamická funkce definovaná vztahem

(4.20)

Její úplný diferenciál je

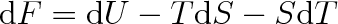V případě vratných změn je podle definičního vztahu (4.13) 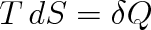, a protože podle prvního termodynamického zákona je 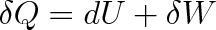, platí pro změnu volné energie

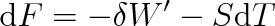(4.21)

Jde-li o vratnou změnu izotermickou (T = konst.), je elementární práce vykonaná soustavou rovna

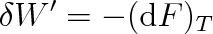(4.22)

Podle vztahu (4.22) je práce, kterou soustava při vratné izotermické změně vykoná, rovna úbytku volné energie. Volná energie představuje tedy tu část energie soustavy, která se za dané teploty spotřebuje na práci vykonanou touto soustavou.

Nemůže-li soustava konat jinou práci než práci objemovou ( ), bude za konstantních hodnot T a V ve shodě s rovnicí (4.21)

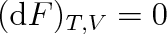Volná entalpie, zvaná též Gibbsova energie, Gibbsova funkce nebo Gibbsův termodynamický potenciál, má význam zejména při změně skupenství látek probíhajících za stálého tlaku a za stálé teploty. Volná entalpie je definována vztahem

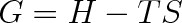(4.23)

v němž H = U + pV značí entalpii (viz vztah (3.28)). Úplný diferenciál volné entalpie je

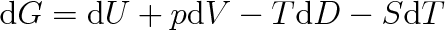Dosadíme-li a za předpokladu, že stavová změna je vratná, , dostaneme pro změnu volné entalpie vztah

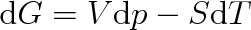(4.24)

Při změnách skupenství a při všech vratných změnách probíhajících za stálého tlaku a teploty (p = konst., T = konst.) je

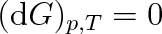(4.25)

Při změnách skupenství látek se volná entalpie nemění. Má tedy táž látka při dvou různých skupenstvích, jež jsou spolu v rovnováze, stejnou volnou entalpii.

Definice stavových funkcí spolu s jejich diferenciály jsou souhrnně uvedeny v následující tabulce:

---

---