---

---

4.6 Entropie

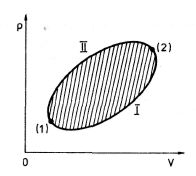
Matematické formulace druhého termodynamického zákona pro vratné děje využijeme k zavedení další funkce. Zvolme v průběhu cyklického děje podle obr. 4-8 dva stavy (1) a (2). Probíhá-li děj ze stavu (l) cestou I do stavu (2) a ze stavu (2) cestou II zpět do stavu (l), a je-li na obou cestách děj vratný, platí

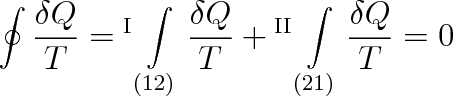Obrátíme-li u druhého integrálu meze, dostaneme, že

Obr. 4-8

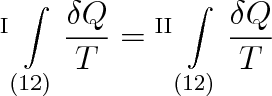(4.19)

Tento vztah dokazuje, že hodnota integrálu z 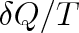při vratné změně ze stavu (1) do stavu (2) není závislá na cestě, po níž děj probíhá, ale závisí pouze na obou stavech soustavy. V této souvislosti zavádíme stavovou funkci S, zvanou entropie. Její přírůstek při vratném ději je definován vztahem

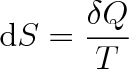(4.13)

Přejde-li soustava po libovolné vratné cestě ze stavu (1) do stavu (2), činí změna entropie

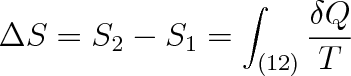(4.14)

kde S₁ je hodnota entropie ve stavu (1), S₂ hodnota entropie ve stavu (2).

Pro vratný cyklický děj je změna entropie (po libovolné uzavřené křivce)

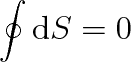(4.15)

Kdykoliv se integrál libovolného výrazu vzatý po uzavřené křivce rovná nule, je výraz za integračním znakem totálním diferenciálem nějaké stavové funkce. V souladu s tím je výraz 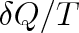totálním diferenciálem entropie, přestože 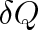samo, jak jsme poznali v čl. 3.2, totálním diferenciálem není. Stává se jím teprve vynásobením integračním faktorem 1/T.

Podobně jako vnitřní energii je možno i entropii určit až na aditivní integrační konstantu. Entropie je dána vztahem

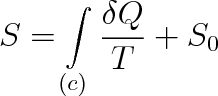(4.16)

v němž S₀ je konstanta, představující hodnotu entropie v základním stavu, tj. při teplotě T₀ = 0 K. Konstantu S₀ je možno zvolit libovolně. Jak ukázal Planck, nejvýhodnější je pro ni hodnota nulová (viz dále čl. 4.8).

Entropie je právě tak jako vnitřní energie aditivní funkcí. To znamená, že se entropie soustavy složené z několika částí rovná součtu entropií těchto částí.

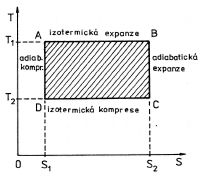
Entropie má pro druhý termodynamický zákon stejný význam jako vnitřní energie pro první termodynamický zákon. Obě tyto stavové funkce zůstávají konstantní u izolovaných soustav. Zatímco vnitřní energie se nemění, je-li soustava izolovaná a uzavřená, entropie zůstává konstantní při vratných změnách adiabatických. Proto vratné adiabatické děje jsou z hlediska entropie izentropic-ké (izoentropické). Této vlastnosti entropie užíváme s výhodou ke grafickému znázornění vratných cyklických dějů v tzv. tepelných diagramech. Jimi rozumíme diagramy v proměnných entropie, teplota - S, T. V těchto diagramech jsou izotermy a adiabaty přímky rovnoběžné s osami souřadnic (obr. 4-9). Izotermic-

Obr. 4-9

ká expanze je spojena s růstem entropie (S₂ > S₁), izotermická komprese s jejím poklesem. Adiabatické změny probíhají izentropicky, a to tak, že při expanzi teplota soustavy klesá (T₂ < T₁), při kompresi roste. Zatímco diagram p, V udává obsahem uzavřené plochy práci W', vykonanou při cyklickém ději po vyznačené cestě, v diagramu T, S je obsah uzavřené plochy rovný teplu

Q₁ - Q'₂ , které soustava získá při cyklickém ději. V obou případech mají však veličiny p dV a T dS jednotku energie.

Vyjádříme-li v matematickém zápisu prvního termodynamického zákona (3.21) diferenciál 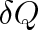pomocí definičního vztahu (4.13) výrazem TdS, dostaneme pro libovolně malou vratnou změnu soustavy, u níž nedochází ke konání jiné práce než objemové (p dV), základní termodynamický vztah

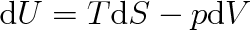(4.17)

Tento vztah představuje spojení prvního a druhého termodynamického zákona.

Prozkoumejme nyní změnu entropie, k niž dochází při stavových změnách ideálního plynu. Aplikace na ideální plyn je zvlášť jednoduchá, neboť jeho vnitřní energie je pouze funkcí teploty a nezávisí na jeho objemu, takže dU = C_V dT (viz vztah (3.23)). Pro infinitezimální vratnou stavovou změnu ideálního plynu platí ve shodě se vztahem (3.21)

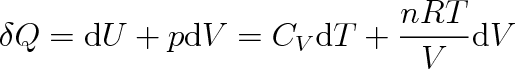když jsme za p dosadili podle stavové rovnice (2.16). Z uvedené rovnice vychází pro libovolně malou změnu entropie

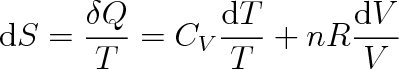Konečná změna entropie ideálního plynu po přechodu ze stavu (1) do stavu (2) je dána vztahem

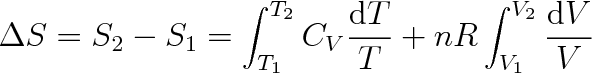který za předpokladu, že C_V není funkcí teploty, má tvar

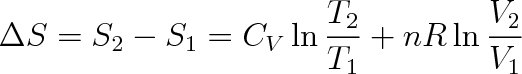Mění-li se teplota plynu izochoricky (V = konst.), je změna entropie

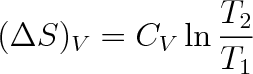Např. pro jednoatomový ideální plyn (helium, argon, apod.) při izochorické změně mezi teplotami 200 °C a 0 °C činí změna entropie pro n = 1 mol

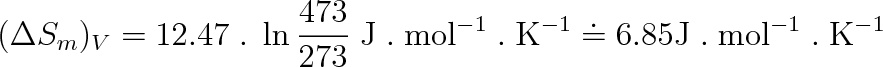Expanduje-li ideální plyn izotermicky (T = konst.) např. na dvojnásobek svého objemu, změní podle výše uvedeného vztahu svou entropii o hodnotu (n = 1 mol)

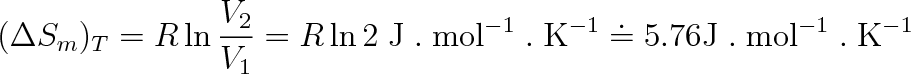Při nevratném cyklickém ději, tj. při cyklu, jehož aspoň jedna část je nevratná, je

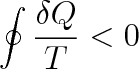V tomto výrazu, zvaném Clausiova nerovnost, neznamená T teplotu soustavy, nýbrž teplotu lázně, s níž si soustava vyměňuje teplo. Pouze u vratných cyklických dějů je teplota T lázně totožná s teplotou soustavy.

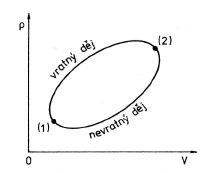Obr. 4-10

Uvažujme o cyklickém ději, při němž soustava přejde ze stavu (1) nevratnou změnou do stavu (2) a z něho vratnou změnou zpět do stavu (1), obr. 4-10. Tento cyklický děj je jako celek nevratný a podle nerovnosti (4.13) platí pro něj

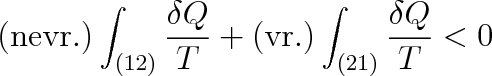a po záměně mezí u druhého integrálu a jednoduché úpravě dostaneme

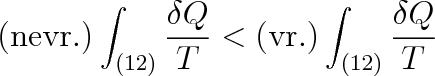Poněvadž integrál po vratné cestě je podle rovnice (4.14) roven změně entropie 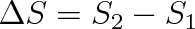, platí při nevratných změnách nerovnost

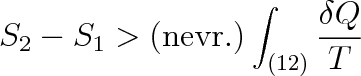(4.18)

V tepelně izolovaných soustavách, v nichž je zabráněno tepelné výměně s okolím, přejde nerovnost (4.18) v nerovnost

(4.19)

vyjadřující princip růstu entropie: Jestliže probíhá v tepelně izolované soustavě jakýkoliv nevratný děj, entropie soustavy roste. Konstantní zůstává jen tehdy, když děj v uvažované soustavě probíhá vratně. Mohou tedy v tepelně izolované soustavě probíhat jen takové děje, při nichž entropie soustavy neklesá.

---

---