 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Termodynamická soustava konající Carnotův cykl může přicházet do styku s libovolným počtem lázní. Předpokládejme, že máme x lázní, jejichž termodynamické teploty jsou T1 , T2 , . . ., Tx. Tepla, která tyto lázně se soustavou vyměňují, označme Q1 , Q2 , ... , Qx . Pro jednoduchost zápisu budeme tepla Qi brát s kladným znaménkem, jestliže soustava teplo přijímá, a se znaménkem záporným, jestliže je odevzdává lázni teploty Ti
Nechť soustava koná cyklický děj, složený z (x - 1) Carnotových cyklů probíhajících mezi teplotami T1 , T2 ; T2 , T3 ; ... ; Tx-1 , Tx . Z obr. 4-7 je zřejmé, že výsledný cyklický děj se realizuje lomenou čarou (na obrázku vyznačeno plně), skládající se z krátkých úseků izoterm a adiabat.
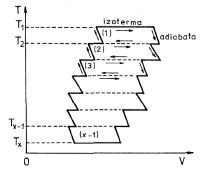Obr. 4-7
Uplatníme-li pro jednotlivé cykly vztah (4.5) při respektování znaménkové konvence, dostaneme postupně vztahy
 |
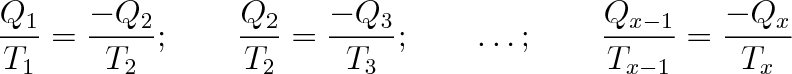Připojíme-li k těmto výrazům ještě vztah Ql /Tl = - Qx/Tx charakterizující výsledný cyklický děj a sečteme-li všechny uvedené vztahy, dostaneme po úpravě vztah
 |
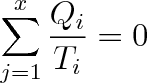(4.11) |
v němž Qi značí teplo, které si při teplotě Ti vyměňuje soustava s i-tou lázní a které může být jak kladné, tak i záporné.
Přejdeme-li k ifinitezimálnímu změnám, můžeme napsat
 |
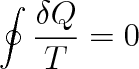(4.12) |
zde symbol
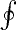znamená křivkový integrál a T je teplota vrstvy.
Symbolem T je označena teplota místa, z něhož soustava přijímá kladné teplo
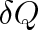nebo jemuž odevzdává záporné teplo -
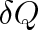. U vratných dějů je mezi teplotou těchto míst a teplotou soustavy jen zanedbatelně malý rozdíl, a proto i zanedbatelně malá odchylka od rovnovážného stavu, což je nutnou podmínkou vratnosti termodynamického děje. Teplota T v rovnici (4.12) může tedy znamenat zároveň i teplotu soustavy. Pro nevratný děj platí vztah
 |
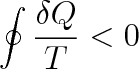(4.13) |
Výrazy (4.12) a (4.13) představují obecnou matematickou formulaci druhého termodynamického zákona. Vycházejí z Thompsonova principu, ale také obráceně, Thompsonův princip z nich vyplývá. Poněvadž není možné, aby v obou výrazech byla všechna tepla
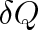kladná, nemůže soustava konající obecný cyklický děj teplo od vnějších těles jenom přijímat, ale musí je některým z nich rovněž odevzdávat. To je ve shodě s principem Thompsonovým, podle něhož není možné periodicky získat práci cyklickým dějem tak, že by soustava teplo jen přijímala a konala ekvivalentní práci.
Ze vztahů (4.12) a (4.13) vyplývá i princip Clausiův. Uvažujme o jednoduchém cyklickém ději, při němž by se přeneslo teplo Q z lázně o teplotě T1 do lázně teploty T2 . Protože jde o dvě lázně, dostaneme po úpravě
 |
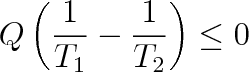Vzhledem k tomu, že Q je v tomto výrazu kladné, musí být T1
T2. To souhlasí s principem Clausiovým, že teplo nemůže samovolně přejít z tělesa studenějšího na těleso teplejší (viz čl. 4.3).
|
|
|
|
|
|
|
|
|