 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Tepelnou kapacitu C definujeme vztahem
 |
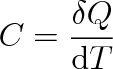(3.9) |
kde
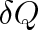je elementární teplo dodané tělesu a dT přírůstek termodynamické teploty tělesa. Jednotkou této veličiny je J . K-1.
Tepelná kapacita tělesa závisí na jeho hmotnosti, chemickém složení, vnitřní stavbě a na podmínkách, za jakých těleso teplo přijímá. Tepelné kapacity se obecně liší, probíhá-li tepelná výměna za konstantního tlaku nebo objemu.
Uvažujme soustavu, jejíž stav je jednoznačně určen objemem V a termodynamickou teplotou T, což znamená, že platí pro tlak p a vnitřní energii U relace
 |
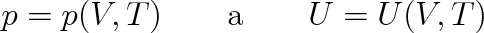Teplo dodané tělesu můžeme vyjádřit pomocí prvního termodynamického zákona a vztahu (3.1) ve tvaru
 |
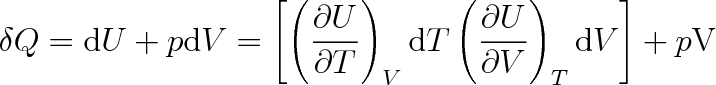(3.10) |
Za nejjednodušší děj můžeme považovat děj izochorický (dV = 0). Potom tepelná kapacita CV při konstantním objemu je
 |
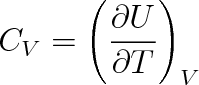(3.11) |
T epelná kapacita Cp při konstantním tlaku je
 |
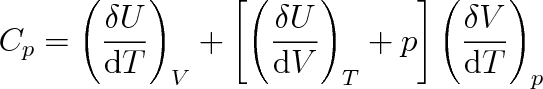(3.12) |
Tepelné kapacity při konstantním objemu a tlaku se liší. Je to celkem pochopitelné, protože při konstantním objemu těleso nekoná práci, naproti tomu při konstantním tlaku práci koná, takže dodané teplo musí ještě krýt i tuto spotřebu energie.
Ukažme si to na příkladu ideálního plynu. Ze stavové rovnice (2.6) vyplývá V = nRT/p, takže
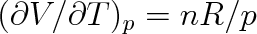. Vnitřní energie ideálního plynu je pouze funkcí T (viz čl. 5.6), proto
.
 |
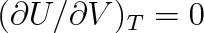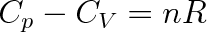(3.14) |
Z toho plyne, že tepelná kapacita C je úměrná hmotnosti m tělesa, a proto se zavádí měrná tepelná kapacita látky, ze které je uvažované těleso.
 |
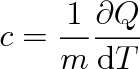(3.15) |
Jednotkou měrné tepelné kapacity je J . kg-1 . K-1.
Měrná tepelná kapacita pevných látek leží mezi 102 J . kg-1 . K-1 až 103 J . kg-1 . K-1. U kapalin jsou v průměru o 1 řád vyšší a dosahují nejvyšší hodnoty u vody (4,182 kJ . kg-1 . K-1 při 20 °C). Plyny mají při pokojové teplotě a za stálého tlaku měrnou tepelnou kapacitu řádově 102 J . kg-1 . K-1 až 103 J . kg-1 . K-1.
Měrná tepelná kapacita není pro látku daného skupenství konstantou, ale závisí na teplotě , ale tato závislost není příliž významná.
 |
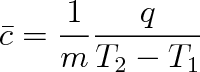(3.16) |
kde Q je teplo potřebné ke zvýšení teploty tělesa hmotnosti m z teploty T1 na teplotu T2. Pro nepříliš velké teplotní rozdíly se střední hodnoty od hodnot skutečných prakticky neliší, proto budeme používat značky c.
U pevných a kapalných látek se rovněž veličiny cV a cp často nerozlišují a v obou případech se značí písmenem c. Vždy se však touto veličinou rozumí měrná tepelná kapacita za stálého tlaku, která se snadněji experimentálně zjišťuje.
U plynu je rozdíl cp-cV znatelný. Např. pro vzduch je roven 0,29 kJ. kg-1 .K-1. Pro ideální plyn platí tzv. Mayerův vztah
 |
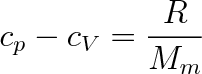(3.19a) |
Veličina
 |
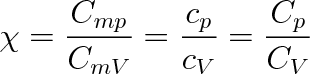(3.20) |
se nazývá Poissonova konstanta. Protože cp > cV , je vždy
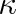> 1.
Uvažujme nyní dvě tělesa tvořící izolovanou soustavu. V čase, kdy soustava vznikla, mělo jedno těleso tepelnou kapacitu c1m1 a teplotu T1, druhé těleso kapacitu c2m2 a teplotu T2 < T1. Za předpokladu, že uvnitř soustavy nedochází ke změně skupenství a ani v ní neprobíhají chemické reakce, dojde po určité době k vyrovnání teplot obou těles na výslednou teplotu T, která leží mezi původními teplotami (T1 > T > T2). Z principu zachování energie vyplývá, že teplo c1m1(T1-T) předané teplejším tělesem tělesu chladnějšímu je rovno teplu c2m2(T-T2), které chladnější těleso přijalo od tělesa teplejšího. Takže musí platit
 |
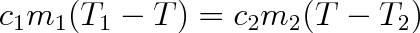Tato rovnice se nazývá směšovací nebo také kalorimetrická rovnice .
Pokud tepelnou izolaci uvažované soustavy od okolí, tvoří např. obal směšovacího kalorimetru, jehož vnitřní nádoba s příslušenstvím (teploměr, míchačka) má tepelnou kapacitu C (stanovenou výpočtem nebo častěji experimentálně) a počáteční teplotu T2, pak kalorimetrická rovnice má tvar
 |
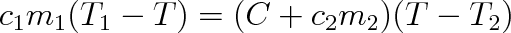Kalorimetrická rovnice umožňuje vypočítat např. měrnou tepelnou kapacitu c1, známe-li c2 a určíme-li měřením veličiny m1, m2, T2, T2,T, resp. C.
|
|
|
|
|
|
|
|
|