Uvažujme soustavu, která je ve stavu termodynamické rovnováhy. Označme tento stav (1). Soustava má určitou vnitřní energii U. Ve stavu (1) soustavě dodáme teplo Q (tepelnou výměnou) a vnější síly na ní vykonají práci W. Tím
soustava zvýší svou vnitřní energii o hodnotu
 U a po jisté době přejde do nového rovnovážného stavu (2).
U a po jisté době přejde do nového rovnovážného stavu (2).
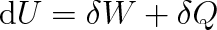 |
(3.6) |
Přírůstek vnitřní energie
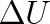 soustavy se rovná součtu práce W vykonané okolními tělesy působícími na soustavu silami a tepla Q odevzdaného okolními tělesy soustavě.
soustavy se rovná součtu práce W vykonané okolními tělesy působícími na soustavu silami a tepla Q odevzdaného okolními tělesy soustavě.
Uvedená formulace se nazývá první termodynamický zákon .
Přírůstek dU je úplný diferenciál, neboť konečná změna vnitřní energie závisí jen na počátečním a konečném stavu soustavy a nezávisí na cestě, po které se změna děla.
Z matematické formulace prvního termodynamického zákona vyplývají jednoduché závěry v těch případech, kdy je termodynamická soustava buď zcela, nebo částečně izolovaná, popřípadě koná kruhový vratný děj:
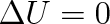 , čili U1 = U2 . V izolované soustavě zůstává vnitřní energie konstantní bez ohledu na to, zda v ní probíhají jakékoli děje (mechanické, tepelné či jiné).
, čili U1 = U2 . V izolované soustavě zůstává vnitřní energie konstantní bez ohledu na to, zda v ní probíhají jakékoli děje (mechanické, tepelné či jiné).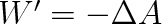 . Soustava koná adiabaticky práci na účet své vnitřní energie.
. Soustava koná adiabaticky práci na účet své vnitřní energie. 2
2
 1). Proto
1). Proto
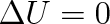 a podle (3.7) je Q = W'. Při kruhovém ději zůstává vnitřní energie konstantní a teplo přijaté soustavou je rovno práci, kterou soustava vykoná.
a podle (3.7) je Q = W'. Při kruhovém ději zůstává vnitřní energie konstantní a teplo přijaté soustavou je rovno práci, kterou soustava vykoná.První termodynamický zákon, který vyjadřuje princip zachování energie, se někdy formuluje v tom smyslu, že nelze sestrojit periodicky pracující stroj, tzv. „perpetuum mobile prvního druhu", který by konal práci bez změny své energie a bez tepelné výměny s okolím.