 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Práci proti vnějším silám koná termodynamická soustava tím, že zvětšuje svůj objem. Soustava může ovšem konat práci i jinak, např. podrobíme-li ji vlivu elektrického nebo magnetického pole. V dalším výkladu budeme prací soustavy rozumět pouze mechanickou práci, spojenou s objemovou změnou soustavy , příspěvky jiných forem energie budeme zanedbávat .
Obr. 3-1
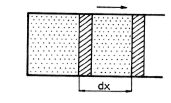
Uvažujme nejprve plyn ve válci s pístem (obr. 3-1). Vypočítáme elementární práci
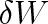vykonanou plynem zvětšením jeho objemu o d V při rovnovážném vratném ději. Tlaková síla plynu na píst má velikost F = pS, kde S je obsah pístu a p tlak plynu. Jestliže se píst posune o vzdálenost dx, vykoná plyn práci
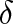W = Fdx = pS dx. Neboli
 |
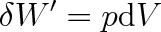(3.1) |
neboť přírůstek objemu dV = S dx.
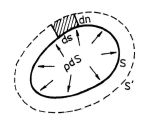Obr. 3-2
Uvažujme např., že plyn je uzavřen v pružném obalu, který se vratně roztahuje (obr. 3-2). Práce vykonaná plynem za tlaku p při přemístění elementu plochy obsahu dS na vzdálenost dn podél normály je p dS. dn, kde p dS = dF je velikost tlakové síly. Je-li tlak p podél celého povrchu konstantní (soustava je v mechanické rovnováze), posune se každý element povrchu ve směru normály o vzdálenost dn, čímž se obsah S plochy obalu zvětší na S' (obr. 3-2).
Elementární práce
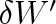, kterou plyn vykoná, je dána součtem všech příspěvků p dS dn po celém povrchu obsahu S, tedy
 |
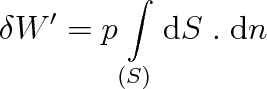Z hlediska použitelnosti tohoto vztahu je nepodstatné, že v obalu je plyn. Nepodstatná je také role existence obalu v uvedeném příkladě. Jeho roli může hrát např. povrch tělesa.
Probíhá-li změna objemu izobaricky (p = konst.), je celková práce vykonaná soustavou
 |
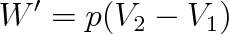(3.3) |
Jde-li o děj, při kterém se mění tlak, je celková práce vykonaná soustavou dána vztahem
 |
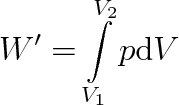(3.2) |
v němž integrační meze Vl a V2 představují objem soustavy na počátku a na konci uvažovaného vratného děje.
Práci vykonanou termodynamickou soustavou nebo práci na soustavě vykonané lze znázornit graficky v p, V diagramu, který vyjadřuje tlak soustavy jako funkci jejího objemu (obr. 3-3).
Vykonají-li při rovnovážném ději vnější síly na soustavě elementární práci dW, a soustava tím přejde ze stavu (1) do stavu (2), pak tato práce je až na znaménko rovna práci dW, kterou vykoná soustava přechodem ze stavu (2) do stavu (1).
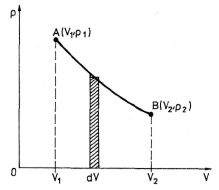Obr. 3-3
Předpokládejme, že z rovnovážného stavu A popsaného objemem V1 a tlakem p1 přejde soustava rovnovážným (vratným) dějem do jiného rovnovážného stavu B
. Přechod z A do B je znázorněn
křivkou AB. Elementární práce
W' je v souladu se vztahem (3.1) znázorněna obsahem vyšrafované plošky. Celková práce W' vykonaná soustavou při přechodu ze stavu A do stavu B je pak podle vztahu (3.2) znázorněna obsahem plochy, která leží pod křivkou AB.
Z p-V diagramu na obr. 3-3 vyplývá, že práce W' je nejen funkcí počátečního a konečného stavu soustavy, ale závisí i na cestě, po níž změna proběhla, tj. na tvaru křivky mezi body A a B. Je tedy práce, stejně jako teplo, veličinou charakterizující děj, jímž soustava prošla.
Z matematického hlediska uvedená skutečnost znamená, že infinitezimální (libovolně malá) veličina
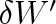(resp.
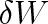) není v obecném případě úplným diferenciálem žádné stavové funkce. Proto pro odlišení od úplného diferenciálu používáme značení
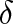místo písmene d.
|
|
|
|
|
|
|
|
|