 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Kinetickou energií
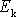hmotného bodu o hmotnosti m
nazýváme výraz
 , |
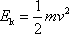(3,10) |
kde v je velikost rychlosti hmotného bodu.
Kinetická energie definovaná výrazem
(3,10)
závisí na
rychlosti bodu vůči soustavě souřadné. Při přechodu od jedné inerciální
soustavy k druhé změní se hodnota kinetické energie o konstantu.
Jelikož však při výpočtech určujících energii srovnáváme vždy energii ve dvou
různých stavech zkoumaného objektu (zde dvě polohy hmotného bodu), není tato
neurčitost v definici kinetické energie
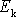podstatná.
Mezi prací vykonanou na hmotný bod a změnou kinetické energie hmotného bodu platí důležitý vztah:
Práce
vykonaná vnějšími silami na hmotný bod,
přejde-li z bodu C do bodu D, je rovna přírůstku kinetické energie hmotného
bodu, tj. rozdílu
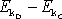mezi kinetickými energiemi hmotného bodu
v bodě D a v bodě C,
 . |
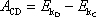(3,11) |
Pro důkaz tvrzení (3,11) použijeme vyjádření práce dle rovnice (3,6)
 . |
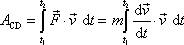V druhé z právě uvedených rovnic jsme užili
vyjádření síly
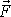dle rovnice
(2,1)
a konstantní hodnotu
hmotnosti m
jsme vytkli před
integrační symbol. Uvědomíme-li si, že platí
 , |
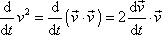můžeme výraz pro
práci
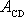dále upravit;
 . |
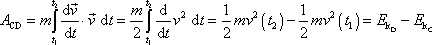V závěrečné úpravě posledního výrazu jsme napsali
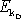za
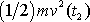, protože výraz
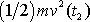zřejmě znamená kinetickou energii hmotného
bodu v bodě D, ve kterém se hmotný bod nachází v čase
. Výraz
značí kinetickou energii hmotného bodu
v bodě C, tj. kinetickou energii hmotného bodu, než na něj práce
byla vykonána. Tím je proveden důkaz tvrzení
(3,11)
.
Z rovnice
(3,11)
plyne též, že kinetická energie
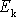a práce A
jsou veličiny se stejným fyzikálním rozměrem, tedy veličiny pro
jejichž kvantitativní vyjádření užíváme stejné jednotky.
|
|
|
|
|
|
|
|
|