---

---

3.4 Potenciální energie, zákon zachování energie

3.4.1 Konzervativní silové pole

Jak plyne z definice (3,4) závisí práce  A vykonaná vnějšími silami na hmotný bod na hodnotách těchto sil v bodech dané dráhy. Může však nastat případ, kdy silové pole mezi výchozím bodem dráhy C a konečným bodem D je takového charakteru, že práce vykonaná silami na hmotný bod nezávisí na volbě cesty mezi body C a D. Silová pole, ve kterých práce mezi libovolnými body nezávisí na cestě, kterou tyto body spojíme, nazýváme konzervativními.

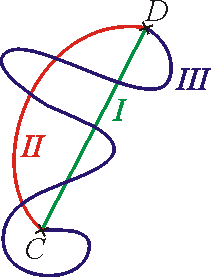
Na obr.12 jsou znázorněny tři cesty z bodu C do bodu D. Je-li silové pole konzervativní, musí být práce stejná pro všechny tři dráhy. Označme práci vykonanou konzervativními silami na hmotný bod, přejde-li z bodu C do D po cestě I, 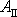práci po cestě II, pak 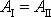. Pohybuje-li se hmotný bod opačným směrem, tj. z bodu D do C např. po dráze II, označíme příslušnou práci . Mluvíme-li o silovém poli, před-pokládáme, že síla v daném místě pole je stále stejná (časovou závislost pole zde neuvažujeme) a pak podle (3,5) platí 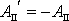. Práce  A   vykonaná konzervativními silami na hmotný bod, přejde-li z bodu C do D po dráze I a potom z D do C po dráze II, . 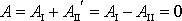Práce  A   vykonaná po zvolené uzavřené křivce je nulová.

V konzervativním silovém poli práce po libovolné uzavřené křivce je nulová. Této vlastnosti konzervativních silových polí se využívá k jejich obecné charakteristice ve vektorové analýze (viz např. [24], kap.7), která je adekvátní matematickou disciplinou k  popisu silových a dalších vektorových polí. Je-li práce po libovolné uzavřené křivce v silovém poli nulová, lze pomocí Stokesovy věty

.

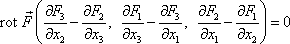Rovnost právě zavedeného vektoru , který se nazývá rotace, nule je užívána jako charakteristika konzervativnosti příslušného silového pole. Je-li v nějaké oblasti v každém bodě rotace síly rovna nule, je v této oblasti silové pole konzervativní. V poslední rovnici jsou uvedeny složky vektoru 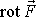, které lze pro libovolný bod silového pole 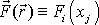vypočítat parciálním derivováním a provedením naznačených algebraických operací.

Jako příklady konzervativních silových polí lze uvést gravitační pole a elektrostatické pole, nekonzervativní charakter mají pole odporujících sil (sil tření) (viz čl.4.4) a také pole magnetické.

3.4.2 Zavedení potenciální energie

V konzervativních silových polích závisí práce vykonaná na určitý hmotný bod, přejde-li z jednoho bodu pole do druhého bodu pole, pouze na poloze těchto bodů. Můžeme zavést veličinu závislou na polohách (tj. na souřadnicích) bodů pole, které nám tuto práci udává. Takové veličině říkáme potenciální energie .

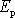Při konkrétním zavádění potenciální energie postupujeme tak, že v jistém bodě O zvolíme určitou hodnotu potenciální energie 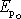. Hodnota potenciální energie v libovolném jiném bodě X konzervativního silového pole je dána rovnicí

(3,12)

kde 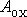je práce vykonaná vnějšími silami na hmotný bod, přejde-li z bodu O do bodu X. Práce 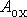je funkcí polohy bodu C. Zvolíme-li soustavu souřadnic s počátkem v bodě O, j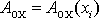e , kde 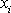jsou souřadnice bodu X. Ve zvolené soustavě souřadné lze psát

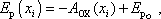(3,13)

kde 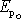  je výše libovolně zvolená hodnota potenciální energie v bodě O. Takto dostáváme potenciální energii vyjádřenou jakožto funkci souřadnic .

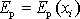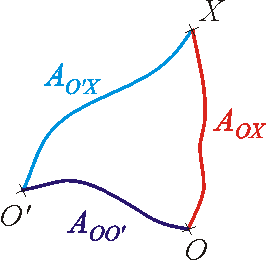Zvolíme-li místo bodu O jiný výchozí bod 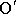, práce 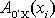a se budou lišit pouze o konstantu , tj. o práci vykonanou na hmotný bod, přejde-li z bodu O do bodu 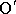. Platí totiž (viz obr. 12´)

.

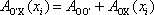Rozdíl funkce

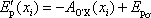a funkce (3,13) je

.

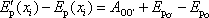Jelikož 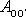, 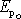a (libovolně zvolená potenciální energie v bodě 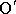) jsou konstantní hodnoty, liší se funkce 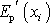a 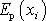pouze konstantu 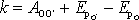, tedy

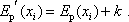Potenciální energie je funkce souřadnic jednoznačně určená až na konstantu. Hodnotu této konstanty určíme, zvolíme-li hodnotu potenciální energie 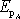v jednom místě konzervativního silového pole, např. v bodě A o souřadnicích 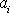, tj. položíme-li . Potom už je hodnota potenciální energie v každém bodě silového pole určena jednoznačně.

Zvolíme dva libovolné body C a D v konzervativním silovém poli a jejich souřadnice označíme 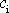a . Z rovnice (3,13) dostáváme pro rozdíl potenciálních energií mezi body C a D vyjádření

.

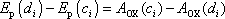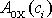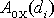Práce je práce vykonaná na hmotný bod, přejde-li z bodu O do bodu C a je práce vykonaná na hmotný bod, přejde-li z bodu O do bodu D. S uvážením rovnice (3,5) lze práci 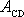vykonanou na hmotný bod, přejde-li z bodu C do bodu D, vyjádřit jako 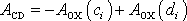, protože cesta z C do O a pak z O do D je jednou z cest z C do D.

Pro rozdíl potenciálních energií mezi body C a D, užijeme-li pro 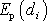označení 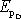a pro 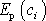označení 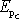, pak můžeme psát

.

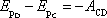(3,14)

Rozdíl 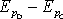 potenciálních energií mezi libovolnými body C a D je roven záporně vzaté práci vykonané vnějšími silami na hmotný bod, přejde-li z bodu C do bodu D.

3.4.3 Zákon zachování energie

Veličina 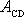v rovnici (3,11) a v rovnici (3,14) má stejný význam. Porovnáním rovnic (3,11) a (3,14) dostáváme

,

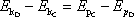neboli

.

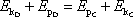(3,15)

Rovnice (3,15) vyjadřuje zákon zachování mechanické energie hmotného bodu . Body C a D jsou voleny libovolně a jsou vázány pouze podmínkou (viz. rovnice (3,11) ), že musí ležet na jedné trajektorii hmotného bodu. Tvrzení obsažené v rovnici (3,15) vyslovíme v tvaru:

Pohybuje-li se hmotný bod v konzervativním silovém poli, je součet jeho kinetické a potenciální energie, který označujeme jako mechanickou energii 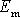, konstantní:

.

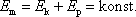(3,16)

Rovnice (3,16) je důsledkem Newtonových zákonů pro konzervativní silová pole. Mechanické zákonitosti lze však budovat i tak, že se nevychází z Newtonových zákonů, ale do čela mechaniky se postaví funkce o rozměru energie, pro ni se stanoví základní rovnice a z nich se potom odvozují další mechanické zákonitosti. O tom se blíže poučíte v teoretické mechanice (např. [11], [12], [15], [16]).

Je třeba si uvědomit, že zákon zachování energie v podobě rovnicí (3,16) platí pouze pokud v systému působí pouze konzervativní síly, v případě nekonzervativních sil je situace složitější.

Zákon zachování energie, zde vyslovený pro pohyb hmotného bodu v konzervativním silovém poli, bývá rozšiřován na děje v různých systémech za přítomnosti konzervativních i nekonzervativních sil. Při tom se zachovává tvar rovnice (3,16) , tj. tvar, kdy součet různých energií je konstantní, a pro zachování správnosti rovnice typu (3,16) se přidávají další formy energie.

Např. při působení odporujících sil (sil typu tření) není mechanická energie 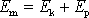hmotného bodu konstantní. Lze ukázat (viz čl.4.4), že působením odporujících sil mechanická energie hmotného bodu klesá. Mluví se o rozptylu disipaci energie a silám, za jejichž působení se mechanická energie systému zmenšuje, se říká disipativní síly . Nejčastěji se působením disipativních sil pohybující systém a jeho okolí zahřejí. Mluvíme zde raději o systému, aby později zavedený pojem vnitřní energie systému nemusel být nevhodně vztahován k jednomu bodu. Přitom makroskopický mechanický pohyb systému může být popsán jako pohyb hmotného bodu. Omezíme se na případ, kdy na systém není vykonána žádná makroskopická práce. Pak změny v okolí započteme do energetických úvah tím, že zavedeme energii, která pohybující se systém opustí, a kterou nazýváme teplem  Q . Jedná se o teplo, které přešlo ze systému do okolí. Zákon zachování energie napíšeme nyní ve tvaru

,

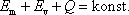(3,17)

kde 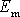je mechanická energie systému a vnitřní energie systému. Vnitřní energii systému lze dále rozložit podle příčin jejího vzniku na několik členů a zákon zachování energie psát ve tvaru analogickém rovnici (3,16) , tedy jako konstantní součet různých druhů energií

.

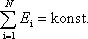V poslední rovnici jedna z 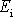odpovídá mechanické energii 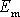, jedna teplu Q   a ostatní různým formám vnitřní energie systému.

zavři

3.4.4 Gradient potenciální energie, ekvipotenciální plocha

Potenciální energie 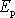zavedená ve stati 3.1.2 je funkcí souřadnic 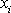; 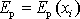, její diferenciál (viz např. [24], kap.12) můžeme napsat ve tvaru

.

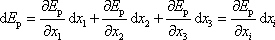(3,18)

Rovnici (3,13) určující funkci lze napsat jako

.

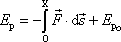(3,19)

Z tohoto zápisu plyne pro diferenciál 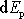vyjádření

.

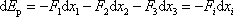(3,20)

Porovnáním rovnic (3,18) a (3,20) dostáváme vztah mezi složkami síly konzervativního silového pole a parciálními derivacemi potenciální energie

,

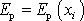
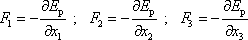stručně zapsáno

.

(3,21)

V poslední rovnici je po dříve zavedené rotaci vektoru 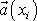značené 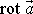užit další z vektorových operátorů užívaných ve vektorové analýze (viz např. [24], kap.7) gradient funkce 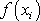značený 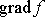. Gradient funkce je vektor, jehož složky jsou rovny parciálním derivacím funkce dle jednotlivých souřadnic;

.

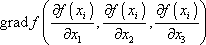(3,38)

Diferenciál funkce d f značí přírůstek funkce. Ten závisí na přírůstcích diferenciálech  d x_i nezávisle proměnných vztahem (srov. (3,18) )

,

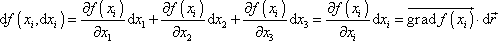(3,39)

v kterém jsme šipkou nad symbolem gradientu zdůraznili jeho vektorový charakter a 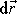označili vektor, jehož složkami jsou přírůstky nezávisle proměnných ; .

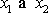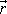Smysl rovnice (3,39) a význam pojmu gradient objasníme na náčrtku připojeném k následující stránce. Pro zjednodušení v něm vykreslíme rovinný případ, tj. případ, kdy funkce  f   je funkcí pouze dvou proměnných . Diferenciální rozvoj funkce  f   provádíme kolem náhodně vybraného bodu o souřadnicích , tedy bodu, který se nachází v místě o polohovém vektoru a který jsme v náčrtku označili A. Přírůstek (diferenciál) funkce d f závisí na volbě vektoru 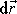, tedy na směru a velikosti přírůstku nezávisle proměnných (diferenciálů  dx_i).

Skalární součin

,

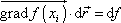(3,40)

tedy udává v lineárním přiblížení rozdíl hodnot funkce  f   mezi bodem o polohovém vektoru (koncový bod vektoru 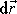) a bodem o polohovém vektoru 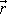(bod A). Na náčrtku jsou vyznačeny křivky stálých hodnot funkce  f . Křivka, kde funkce  f   má stejnou hodnotu jako v bodě A, je označena  f _A   ostatní 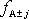. Volíme-li vektor 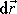ve směru křivky  f _A, je diferenciál d f   nulový. Z rovnice (3,40) pak plyne, že je kolmý ke křivce f_A   v bodě A. Je-li skalární součin roven nule a oba vektory jej tvořící jsou nenulové, musí tyto vektory být vzájemně kolmé. Gradient je kolmý ke křivkám v troj-rozměrném případě k plochám stálých hodnot funkce, míří tedy ve směru maximální rychlosti růstu funkce. To jsou charakteristické vlastnosti gradientu funkce.

Je-li funkcí, jejíž gradient určujeme, potenciální energie E_p , míří  grad E_p   ve směru jejího maximálního růstu a je kolmý k ploše stálé (konstantní) hodnoty této energie, kterou nazýváme ekvipotenciální plochou . Rovnici (3,21) pak můžeme interpretovat tak, že síla míří přesně proti směru maximálního růstu potenciální energie.

---

---