Často je důležité kromě celkového množství vykonané práce znát též, jak rychle je práce konána. Proto se zavádí další veličina výkon P vztahem
Výkon P
je zaveden jako časová derivace práce.
Máme-li mít práci A
vykonanou silou
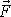 na hmotný bod vyjádřenu jako funkci času,
užijeme rovnici
(3,6)
s proměnnou vrchní mezí integrálu:
na hmotný bod vyjádřenu jako funkci času,
užijeme rovnici
(3,6)
s proměnnou vrchní mezí integrálu:
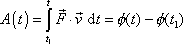 . . |
Funkce
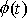 je primitivní funkcí k funkci
je primitivní funkcí k funkci
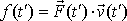 ,
,
Konstanta jen rozlišuje jednotlivé primitivní funkce a pro další úvahy je nepodstatná.
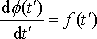 , ale též
, ale též
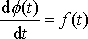 . Dosadíme-li takto vyjádřenou práci
. Dosadíme-li takto vyjádřenou práci
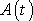 do definiční rovnice
(3,7)
pro výkon P,
dostáváme
do definiční rovnice
(3,7)
pro výkon P,
dostáváme
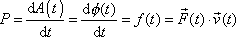 . . |
Je to důležité vyjádření pro
okamžitý výkon síly
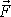 působící na hmotný bod pohybující se
rychlostí
působící na hmotný bod pohybující se
rychlostí
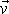 ;
;
Narůstá-li práce rovnoměrně
s časem a čas je měřen od okamžiku, kdy se práce začala konat (v čase
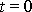 práce
práce
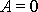 ), redukuje se rovnice
(3,7)
na často užívaný
vztah
), redukuje se rovnice
(3,7)
na často užívaný
vztah
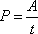 . . |
(3,9) |