 Pro vystižení úhrnného působení síly na hmotný bod, který vykonal pohyb po zadané dráze,
se zavádí veličina práce. Vykonal-li hmotný bod pohyb po
úsečce délky s z bodu C dobodu D a v každém bodě na něj působila
stejná síla
Pro vystižení úhrnného působení síly na hmotný bod, který vykonal pohyb po zadané dráze,
se zavádí veličina práce. Vykonal-li hmotný bod pohyb po
úsečce délky s z bodu C dobodu D a v každém bodě na něj působila
stejná síla
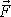 , pak prací A
, kterou síla
, pak prací A
, kterou síla
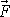 vykonala na hmotný bod podél dráhy, nazveme
výraz
vykonala na hmotný bod podél dráhy, nazveme
výraz
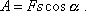 |
(3,1) |
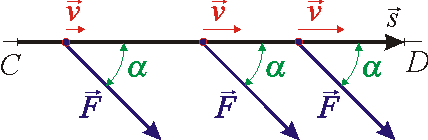
Stejnou silou rozumíme sílu, která v každém bodě dráhy
má stejnou velikost a svírá v každém bodě dráhy s úsečkou stejný
úhel a
(viz obr.10). Úhel a
měříme jako úhel mezi silou
 a vektorem
a vektorem
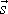 , jehož velikost je rovna délce úsečky s
a který má počátekv bodě C a konec v bodě D. S takto zavedeným vektorem
, jehož velikost je rovna délce úsečky s
a který má počátekv bodě C a konec v bodě D. S takto zavedeným vektorem
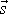 můžeme výraz
(3,1)
přepsat na tvar
můžeme výraz
(3,1)
přepsat na tvar
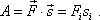 |
(3,2) |
 Výrazy
Výrazy
 , resp.
, resp.
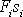 , značí skalární součin vektorů
, značí skalární součin vektorů
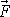 a
a
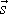 . Druhý výraz lze rozepsat dle
sumačního pravidla
. Druhý výraz lze rozepsat dle
sumačního pravidla
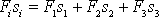 (viz dodatek D.1). Pohybuje-li se hmotný bod
z bodu C do bodu D po úseku dráhy obecného tvaru (viz obr.11) nebo v případě, kdy při pohybu po úsečce
nepůsobí na hmotný bod ve všech bodech stejná síla
(viz dodatek D.1). Pohybuje-li se hmotný bod
z bodu C do bodu D po úseku dráhy obecného tvaru (viz obr.11) nebo v případě, kdy při pohybu po úsečce
nepůsobí na hmotný bod ve všech bodech stejná síla
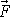 , je nutno definici práce
(3,1)
rozšířit. V tomto obecném případě se
práce A
zavádí jako křivkový
integrál (viz [24], kap.14)
, je nutno definici práce
(3,1)
rozšířit. V tomto obecném případě se
práce A
zavádí jako křivkový
integrál (viz [24], kap.14)
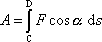 . . |
(3,3) |
Velikost
síly F
i kosinus úhlu a ,
který svírá směr síly
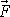 s tečnou
s tečnou
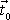 dráhy orientovanou ve směru rostoucího
parametru s
, jsou funkcemi parametru s . Parametr s
značí délku oblouku
. Objasníme tento pojem. Vezmeme-li libovolné dva body A a B dráhy,
pak integrál
dráhy orientovanou ve směru rostoucího
parametru s
, jsou funkcemi parametru s . Parametr s
značí délku oblouku
. Objasníme tento pojem. Vezmeme-li libovolné dva body A a B dráhy,
pak integrál
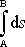 je roven délce dráhy mezi body A a B.
Velikost rychlosti
je roven délce dráhy mezi body A a B.
Velikost rychlosti
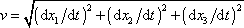 |
hmotného bodu, který se pohybuje po trajektorii
(1,3)
 , je možno též vyjádřit jako derivaci délky oblouku (délky dráhy) podle času
t:
, je možno též vyjádřit jako derivaci délky oblouku (délky dráhy) podle času
t:
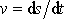 . Z posledního výrazu pro v
plyne vztah
. Z posledního výrazu pro v
plyne vztah
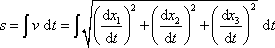 |
mezi délkou oblouku s
a časem t
, který byl jako parametr užíván v 1. kapitole při popisu
trajektorií, a tedy i drah hmotných bodů. Poslední vztah určuje funkci
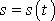 ve tvaru neurčitého integrálu, určuje tedy
parametr s
až na libovolnou
konstantu, která odpovídá libovůli ve volbě bodu, od něhož délku oblouku
počítáme. Je-li
ve tvaru neurčitého integrálu, určuje tedy
parametr s
až na libovolnou
konstantu, která odpovídá libovůli ve volbě bodu, od něhož délku oblouku
počítáme. Je-li
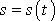 , lze za předpokladů, které zpravidla pokládáme za splněné, najít funkční
závislost
, lze za předpokladů, které zpravidla pokládáme za splněné, najít funkční
závislost
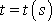 a v parametrickém vyjádření drah
hmotných bodů nahradit parametr t délkou oblouku
s;
a v parametrickém vyjádření drah
hmotných bodů nahradit parametr t délkou oblouku
s;
 . Potom
. Potom
 a výraz
a výraz
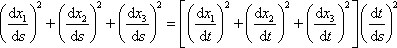 . . |
Za obvyklých předpokladů
 . Výraz v hranaté závorce je
. Výraz v hranaté závorce je
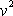 , a tedy, jelikož
, a tedy, jelikož
 , je
, je
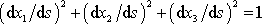 neboli v diferenciálním tvaru
neboli v diferenciálním tvaru
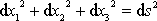 . Poslední rovnice ukazuje, že parametr s
v parametrických rovnicích křivky
. Poslední rovnice ukazuje, že parametr s
v parametrických rovnicích křivky
 je
délkou oblouku.
je
délkou oblouku.
Velikost síly F
i kosinus úhlu
 jsou v integrálu
(3,3)
považovány za
funkce parametru s
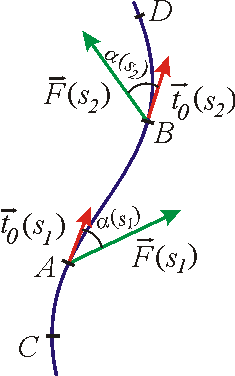
. Na obr.11 jsou naznačeny veličiny F ( s) a
jsou v integrálu
(3,3)
považovány za
funkce parametru s
. Na obr.11 jsou naznačeny veličiny F ( s) a
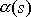 pro dva body A a B uvažované křivky, pro
které parametr s
nabývá hodnot s1 a s2.
Jelikož
pro dva body A a B uvažované křivky, pro
které parametr s
nabývá hodnot s1 a s2.
Jelikož
 a
a
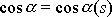 , je i výraz
, je i výraz
 funkcí parametru s, tedy
funkcí parametru s, tedy
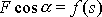 a integrál
(3,3)
lze chápat jako křivkový
integrál
a integrál
(3,3)
lze chápat jako křivkový
integrál
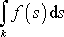 z funkce vyjádřené v závislosti na
délce oblouku s
. Při znalosti funkce
z funkce vyjádřené v závislosti na
délce oblouku s
. Při znalosti funkce
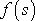 se křivkový integrál
se křivkový integrál
 integruje stejným způsobem jako obyčejný
integrál
integruje stejným způsobem jako obyčejný
integrál
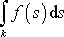 . Integrál
(3,3)
bývá stručně zapisován ve tvaru
. Integrál
(3,3)
bývá stručně zapisován ve tvaru
, kde
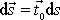 a
a
 je jednotkový vektor ve směru tečny. Kladný
smysl
je jednotkový vektor ve směru tečny. Kladný
smysl
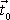 souhlasí se smyslem růstu parametru s .
Tedy
souhlasí se smyslem růstu parametru s .
Tedy
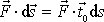 a uvědomíme-li si, jak byl v rovnici
(3,3)
zaveden úhel
a uvědomíme-li si, jak byl v rovnici
(3,3)
zaveden úhel
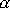 , je
, je
 (nezapomeň, že
(nezapomeň, že
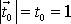 ). Tedy
). Tedy
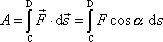 ; ; |
výrazy (3,3) a (3,4) pro práci jsou ekvivalentní.
Z vlastností integrálu plyne
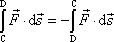 . . |
Práce
 vykonaná silou
vykonaná silou
 na hmotný bod, přejde-li z bodu C do
bodu D a práce
na hmotný bod, přejde-li z bodu C do
bodu D a práce
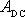 vykonaná silou
vykonaná silou
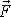 na hmotný bod, přejde-li z bodu D do
bodu C, jsou stejně velké, ale opačného znaménka
na hmotný bod, přejde-li z bodu D do
bodu C, jsou stejně velké, ale opačného znaménka
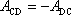 . . |
(3,5) |
Předpokládáme ovšem, že bod se pohybuje z C do D a z D do C po stejné dráze a silové působení podél této dráhy je stejné pro oba pohyby.
Práce
(3,3)
nebo
(3,4)
závisí přímo pouze na tvaru dráhy a
působící síle a nezávisí na tom, jak hmotný bod dráhu probíhá. Někdy je však
výhodné počítat práci pro konkrétní pohyb hmotného bodu daný parametrickými
rovnicemi
 . Výraz
(3,4)
pro práci můžeme pak upravit následujícím způsobem
. Výraz
(3,4)
pro práci můžeme pak upravit následujícím způsobem
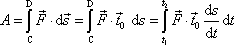 . . |
Uvědomíme-li si dále, že
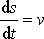 a
a
 , můžeme konečně práci A psát ve tvaru
, můžeme konečně práci A psát ve tvaru
Čas
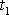 je okamžik, kdy se hmotný bod nachází
v bodě C a
je okamžik, kdy se hmotný bod nachází
v bodě C a
 okamžik, kdy se hmotný bod nachází
v bodě D. V druhé části rovnice
(3,6)
je použito složkové symboliky a
sumačního pravidla (viz dodatek D.1).
okamžik, kdy se hmotný bod nachází
v bodě D. V druhé části rovnice
(3,6)
je použito složkové symboliky a
sumačního pravidla (viz dodatek D.1).