V okolí těles, na hranicích deformovaných těles, v okolí elektricky nabitých částic, v okolí vodičů protékaných elektrickými proudy a v řadě dalších případů, lze stanovit silové působení, které při známém rozložení objektů a udání několika dalších podmínek (např. zda jde o působení na elektricky nabité nebo nenabité těleso nebo zda lze zanedbat vedlejší vlivy) je vždy stejné. Známe-li silové působení, tj. známe-li rozložení sil v nějakém prostoru neboli, jak říkáme, známe-li silové pole, můžeme dle druhého Newtonova zákona určit pohyb hmotného bodu v tomto silovém poli. Určujeme-li pohyb hmotného bodu v daném silovém poli, říkáme, že řešíme pohybovou rovnici hmotného bodu.
Silové pole v okolí Země, omezíme-li se na prostor
s délkovými rozměry malými oproti poloměru Země, lze vystihnout výrazem
(2,5)
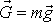 . Dosadíme-li sílu
. Dosadíme-li sílu
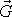 za
za
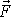 do druhého Newtonova zákona
(2,1)
, dostaneme
pohybovou rovnici
do druhého Newtonova zákona
(2,1)
, dostaneme
pohybovou rovnici
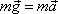 |
(2,7) |
pro pohyb hmotného bodu o hmotnosti m
v tíhovém poli
(2,5)
. Tíhové
zrychlení
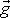 je konstantní vektor, do jeho směru položíme
třetí osu kartézské souřadnicové soustavy. Kladný smysl osy zvolíme opačně, než
je kladný smysl vektoru
je konstantní vektor, do jeho směru položíme
třetí osu kartézské souřadnicové soustavy. Kladný smysl osy zvolíme opačně, než
je kladný smysl vektoru
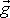 ; osa
; osa
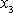 míří tedy svisle vzhůru. Osy
míří tedy svisle vzhůru. Osy
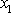 a
a
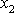 leží ve vodorovné rovině a jejich směry
nemusíme blíže určovat. Rovnice
(2,7)
rozepíšeme do složek v takto zvolené
souřadnicové soustavě, dostaneme
leží ve vodorovné rovině a jejich směry
nemusíme blíže určovat. Rovnice
(2,7)
rozepíšeme do složek v takto zvolené
souřadnicové soustavě, dostaneme
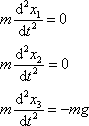 , , |
(2,8) |
neboť síla
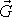 ve zvolené souřadnicové soustavě má
složky
ve zvolené souřadnicové soustavě má
složky
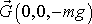 . Řešením, tj. integrací rovnic
(2,8)
, získáme hledané parametrické rovnice
pohybu hmotného bodu;
. Řešením, tj. integrací rovnic
(2,8)
, získáme hledané parametrické rovnice
pohybu hmotného bodu;
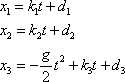 . . |
(2,9) |
V rovnicích
(2,9)
jsou
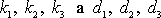 libovolné konstanty. Všechna řešení rovnic
(2,8)
lze zapsat ve tvaru
(2,5)
, a tedy rovnice
(2,9)
popisují jakýkoliv pohyb
, který hmotný bod může v silovém poli
(2,5)
konat. Předpokládáme
samozřejmě , že na hmotný bod nepůsobí jiná síla než síla
(2,5)
, tedy ani žádná
vazbová síla, která by jej např. mohla udržovat na nakloněné rovině.
libovolné konstanty. Všechna řešení rovnic
(2,8)
lze zapsat ve tvaru
(2,5)
, a tedy rovnice
(2,9)
popisují jakýkoliv pohyb
, který hmotný bod může v silovém poli
(2,5)
konat. Předpokládáme
samozřejmě , že na hmotný bod nepůsobí jiná síla než síla
(2,5)
, tedy ani žádná
vazbová síla, která by jej např. mohla udržovat na nakloněné rovině.
Rovnice
(2,9)
jsou obecné rovnice vrhů
. Konstanty
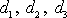 jsou souřadnicemi bodu D
jsou souřadnicemi bodu D
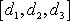 , ve kterém se hmotný bod nachází v čase
, ve kterém se hmotný bod nachází v čase
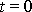 , jak snadno zjistíme, dosadíme-li čas
, jak snadno zjistíme, dosadíme-li čas
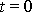 do rovnic
(2,9)
. Derivujeme-li každou
z rovnic
(2,9)
dle času t
a do derivovaných rovnic dosadíme čas
do rovnic
(2,9)
. Derivujeme-li každou
z rovnic
(2,9)
dle času t
a do derivovaných rovnic dosadíme čas
 , zjistíme, že konstanty
, zjistíme, že konstanty
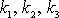 jsou složkami vektoru rychlosti
jsou složkami vektoru rychlosti
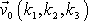 , kterou má hmotný bod v čase
, kterou má hmotný bod v čase
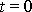 . Známe-li tedy polohu hmotného bodu D a jeho rychlost
. Známe-li tedy polohu hmotného bodu D a jeho rychlost
 v čase
v čase
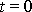 , je pohyb hmotného bodu rovnicemi
(2,9)
jednoznačně určen. Polohu hmotného bodu
a jeho rychlost v čase
, je pohyb hmotného bodu rovnicemi
(2,9)
jednoznačně určen. Polohu hmotného bodu
a jeho rychlost v čase
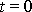 nazýváme počátečními podmínkami pohybu. Zvolíme-li např.
nazýváme počátečními podmínkami pohybu. Zvolíme-li např.
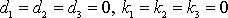 , dostáváme z rovnic
(2,9)
rovnici volného pádu
, dostáváme z rovnic
(2,9)
rovnici volného pádu
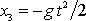 , která je shodná s rovnicí
(2,4)
, uvědomíme-li si opačnou orientaci osy
, která je shodná s rovnicí
(2,4)
, uvědomíme-li si opačnou orientaci osy
 v rovnicích
(2,4)
a
(2,9)
. Zvolíme-li
např.
v rovnicích
(2,4)
a
(2,9)
. Zvolíme-li
např.
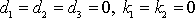 ,
,
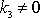 , dostáváme podle znaménka konstanty
, dostáváme podle znaménka konstanty
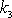 buď vrh svislý vzhůru nebo vrh svislý dolů. Volba
buď vrh svislý vzhůru nebo vrh svislý dolů. Volba
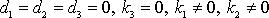 odpovídá vodorovným vrhům. Konkrétní volbou
odpovídá vodorovným vrhům. Konkrétní volbou
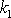 a
a
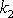 je určen směr vodorovného vrhu. Volba
je určen směr vodorovného vrhu. Volba
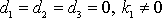 ,
,
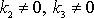 , odpovídá šikmým vrhům. Pro všechny dosud uváděné vrhy jsme volili
, odpovídá šikmým vrhům. Pro všechny dosud uváděné vrhy jsme volili
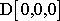 , tj. v čase
, tj. v čase
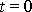 polohu bodu v počátku souřadnicové
soustavy. Volba nenulových hodnot
polohu bodu v počátku souřadnicové
soustavy. Volba nenulových hodnot
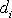 umožňuje vyšetřovat pohyby bodů, které
v čase
umožňuje vyšetřovat pohyby bodů, které
v čase
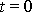 se nenacházejí v počátku soustavy
souřadnic, což je zvláště důležité pro vyšetřování vzájemných pohybů dvou a
více hmotných bodů pohybujících se v daném silovém poli.
se nenacházejí v počátku soustavy
souřadnic, což je zvláště důležité pro vyšetřování vzájemných pohybů dvou a
více hmotných bodů pohybujících se v daném silovém poli.
zavři
Jako druhý příklad na řešení pohybové rovnice budeme hledat
, jak se pohybuje hmotný bod vázaný na přímku, na nějž působí síla úměrná
výchylce mířící proti výchylce. Přesněji síla, která míří k jednomu bodu
přímky a jejíž velikost roste úměrně se vzdáleností od tohoto bodu. Zvolíme-li
ve směru přímky souřadnici x
s počátkem v bodě, ke kterému míří síla, můžeme pro působící sílu napsat
vyjádření
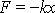 , kde konstanta k je kladná; k>0.
, kde konstanta k je kladná; k>0.
Pohybová rovnice pro pohyb hmotného bodu hmotnosti m v tomto silovém poli má tvar
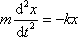 . . |
(2,10) |
Je to rovnice, jejímž řešením máme určit neznámou
funkci
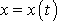 . Jelikož se v této rovnici kromě neznámé funkce
. Jelikož se v této rovnici kromě neznámé funkce
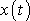 vyskytují i její derivace (zde druhá derivace
vyskytují i její derivace (zde druhá derivace
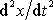 ), mluvíme o diferenciální rovnici. Funkce,
která splňuje rovnici
(2,10)
, musí mít tu vlastnost, že její druhá derivace je
až na jistou konstantu rovna záporně vzaté funkci samotné. Tuto vlastnost mají
harmonické funkce
), mluvíme o diferenciální rovnici. Funkce,
která splňuje rovnici
(2,10)
, musí mít tu vlastnost, že její druhá derivace je
až na jistou konstantu rovna záporně vzaté funkci samotné. Tuto vlastnost mají
harmonické funkce
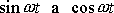 . Položíme-li
. Položíme-li
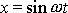 , dostaneme
, dostaneme
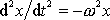 a po dosazení těchto výrazů do rovnice
(2,10)
dostaneme
a po dosazení těchto výrazů do rovnice
(2,10)
dostaneme
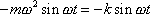 . . |
(2,11) |
Rovnici (2,11) můžeme splnit pro všechna t, položíme-li
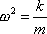 . . |
(2,12) |
Tedy funkce
 , když
, když
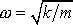 , je řešením rovnice
(2,10)
. Stejným postupem lze zjistit, že i funkce
, je řešením rovnice
(2,10)
. Stejným postupem lze zjistit, že i funkce
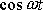 s
s
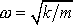 je řešením rovnice
(2,10)
. Řešením je i každá funkce
je řešením rovnice
(2,10)
. Řešením je i každá funkce
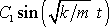 a
a
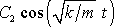 a též součet těchto funkcí
a též součet těchto funkcí
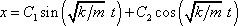 , , |
(2,13) |
kde
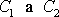 jsou libovolné konstanty. O tom , že funkce
(2,13)
je řešením rovnice
(2,10)
se lze přesvědčit, dosadíme-li ji do rovnice
(2,10)
, kde samozřejmě na levé straně dosazujeme druhou derivaci funkce
(2,13)
.
jsou libovolné konstanty. O tom , že funkce
(2,13)
je řešením rovnice
(2,10)
se lze přesvědčit, dosadíme-li ji do rovnice
(2,10)
, kde samozřejmě na levé straně dosazujeme druhou derivaci funkce
(2,13)
.
Z teorie diferenciálních rovnic (např. [24] kap.17) plyne, že obecné řešení rovnice typu (2,10) dostaneme, najdeme-li její dvě lineárně nezávislá řešení
Lineárně nezávislé jsou takové dvě funkce , pro které nelze najít konstantu C takovou, aby pro všechny hodnoty nezávisle proměnné t platilo .
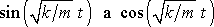 jsou dvě lineárně nezávislá řešení (nelze najít konstantu C
takovou, aby pro všechna t
platilo
jsou dvě lineárně nezávislá řešení (nelze najít konstantu C
takovou, aby pro všechna t
platilo
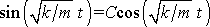 ) rovnice
(2,10)
a výraz
(2,13)
je jejich
lineární kombinací, tedy funkce
(2,13)
je obecným řešením rovnice
(2,10)
.
Obecné řešení diferenciální rovnice je takové řešení, v jehož tvaru lze
zapsat všechna její řešení. Tedy neexistuje žádné řešení rovnice
(2,10)
, které
by nebylo možné zapsat v tvaru
(2,13)
. Zde je však třeba upozornit, že
funkci
(2,13)
je možno též psát v ekvivalentním tvaru (viz rovnice
(1,25)
,
(1,29)
a
(1,30)
)
) rovnice
(2,10)
a výraz
(2,13)
je jejich
lineární kombinací, tedy funkce
(2,13)
je obecným řešením rovnice
(2,10)
.
Obecné řešení diferenciální rovnice je takové řešení, v jehož tvaru lze
zapsat všechna její řešení. Tedy neexistuje žádné řešení rovnice
(2,10)
, které
by nebylo možné zapsat v tvaru
(2,13)
. Zde je však třeba upozornit, že
funkci
(2,13)
je možno též psát v ekvivalentním tvaru (viz rovnice
(1,25)
,
(1,29)
a
(1,30)
)
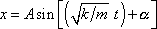 . . |
(2,14) |
Řešením pohybové rovnice
(2,10)
jsme zjistili, že hmotný bod
vázaný na přímku, na nějž působí síla, jejíž velikost je úměrná vzdálenosti od
jistého bodu a která míří z obou stran k tomuto bodu, koná
harmonický kmit s rovnovážnou
polohou v bodě, ke kterému síla míří. Konstanty A, a
v rovnici
(2,14)
, resp.
 v rovnici
(2,13)
lze určit z počátečních podmínek pohybu, tj. obvykle
z výchylky
v rovnici
(2,13)
lze určit z počátečních podmínek pohybu, tj. obvykle
z výchylky
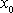 a rychlosti
a rychlosti
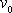 hmotného bodu v čase
hmotného bodu v čase
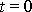 . Frekvence kmitů je dána výrazem
(2,12)
, tedy závisí na hmotnosti
m hmotného bodu a na tom, jak prudce vzrůstá
velikost síly F se vzdáleností od rovnovážné polohy. Je-li síla
F realizována pružinou, odpovídá konstanta k
tuhosti pružiny.
. Frekvence kmitů je dána výrazem
(2,12)
, tedy závisí na hmotnosti
m hmotného bodu a na tom, jak prudce vzrůstá
velikost síly F se vzdáleností od rovnovážné polohy. Je-li síla
F realizována pružinou, odpovídá konstanta k
tuhosti pružiny.
Výsledek získaný řešením rovnice (2,10) bylo možno očekávat, když jsme v čl. 2.2 zjistili, že harmonický pohyb (harmonický kmit) způsobuje síla mířící do rovnovážné polohy, jejíž velikost je úměrná výchylce bodu z rovnovážné polohy. Ovšem, zjistíme-li sílu, která působí na bod konající daný pohyb, nemůžeme ještě nic říci o tom, zda za působení stejné síly nemůže vzniknout i jiný druh pohybu. Teprve řešení (2,13) pohybové rovnice (2,10) , víme-li dle citované matematické věty, že je to řešení obecné, nám umožňuje vyslovit tvrzení:
Harmonický kmit je jediným pohybem, který může vzniknout
v silovém poli vyjádřeném rovnicí
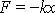 , tedy v případě, kdy na hmotný bod vázaný na přímku působí síla úměrná
výchylce a mířící proti výchylce.
, tedy v případě, kdy na hmotný bod vázaný na přímku působí síla úměrná
výchylce a mířící proti výchylce.
zavři
Obvykle se
v obecných úvahách předpokládá, že síla
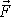 je funkcí všech souřadnic, všech složek
rychlosti a též přímou (explicitní) funkcí času t.
je funkcí všech souřadnic, všech složek
rychlosti a též přímou (explicitní) funkcí času t.
V této obvykle uvažované obecnosti vynecháváme případy, kdy síla je funkcí vyšších derivací souřadnic než prvých, tj. rychlostí. Takové síly se např. uvažují v reologických úvahách. O reologii pojednáme v II. části této knihy.
Předpokládá se tedy, že
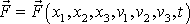 stručně (viz D.I) zapsáno
stručně (viz D.I) zapsáno
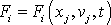 . Pohybovou rovnici pro pohyb hmotného bodu v tomto silovém poli pak píšeme
v tvaru
. Pohybovou rovnici pro pohyb hmotného bodu v tomto silovém poli pak píšeme
v tvaru
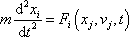 . . |
(2,15) |
Je to soustava tří diferenciálních rovnic druhého řádu
(nejvyšší derivace je druhá derivace), tedy soustava tří rovnic pro určení tří
neznámých funkcí
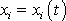 . Přitom zřejmě, např. v prvé z rovnic
(2,15)
se na pravé straně může
vyskytovat nejen funkce
. Přitom zřejmě, např. v prvé z rovnic
(2,15)
se na pravé straně může
vyskytovat nejen funkce
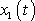 a její derivace
a její derivace
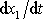 , ale i funkce
, ale i funkce
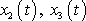 a jejich derivace
a jejich derivace
 . Je proto nutné nejprve separovat diferenciální rovnice pro jednotlivé
funkce
. Je proto nutné nejprve separovat diferenciální rovnice pro jednotlivé
funkce
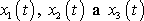 a potom tyto rovnice řešit. Postup může být
složitý a funkce
a potom tyto rovnice řešit. Postup může být
složitý a funkce
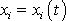 řešící rovnice nemusí ani být takové, aby je
bylo možno zapsat ve tvaru běžně užívaných funkcí. V tomto případě říkáme,
že rovnice nemají analytické řešení. Můžeme je ale řešit
přibližnými metodami.
řešící rovnice nemusí ani být takové, aby je
bylo možno zapsat ve tvaru běžně užívaných funkcí. V tomto případě říkáme,
že rovnice nemají analytické řešení. Můžeme je ale řešit
přibližnými metodami.
Metodami, jakými lze upravovat pohybové rovnice (2,15) na výhodnější tvar, resp. metodami, jak je lze nahradit obsahově ekvivalentními a snáze matematicky zpracovatelnými rovnicemi, se zabývá teoretická mechanika, speciálně její část nazvaná analytická mechanika (např. [11], [12], [14], [15], [16]).
Nehledě na formální potíže při konkrétním řešení rovnic
(2,15)
, má toto řešení opět tvar nám známý z dvou probraných příkladů.
Určuje celou třídu funkcí, které vyhovují rovnicím
(2,15)
, neboli určuje
všechny možné pohyby v daném silovém poli
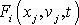 . Z této třídy funkcí konkrétní pohyb hmotného bodu vybereme stanovením
volitelných konstant ve výrazech pro funkce
. Z této třídy funkcí konkrétní pohyb hmotného bodu vybereme stanovením
volitelných konstant ve výrazech pro funkce
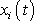 . Nejběžnější způsob stanovení těchto konstant je udání počátečních podmínek
pohybu. Jsou-li udány počáteční podmínky, je pohyb hmotného bodu v daném
silovém poli jednoznačně určen. Nejlépe si způsob řešení pohybových rovnic
vysvětlíme na příkladu pohybu v
tíhovém poli Země
a
v poli síly úměrné výchylce
.
. Nejběžnější způsob stanovení těchto konstant je udání počátečních podmínek
pohybu. Jsou-li udány počáteční podmínky, je pohyb hmotného bodu v daném
silovém poli jednoznačně určen. Nejlépe si způsob řešení pohybových rovnic
vysvětlíme na příkladu pohybu v
tíhovém poli Země
a
v poli síly úměrné výchylce
.
Numerické řešení pohybových rovnic
Při numerickém řešení pohybové rovnice hmotného bodu obvykle
vycházíme z počátečních podmínek pohybu a sledujeme, jak se pohyb
v následujícím čase působením sil vyvíjí. Pohybovou rovnici
(2,1)
přepíšeme
do tvaru
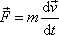 |
(2,30) |
a rovnici převedeme na diferenciální tvar
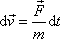 . . |
(2,31) |
Vztah mezi proměnnými diferenciály nahradíme vztahem mezi
konečnými přírůstky (diferencemi) Dt času a
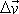 rychlostí
rychlostí
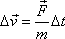 . . |
(2,32) |
Diferenciální rovnici nahradíme diferenční rovnicí. Zvolíme
obvykle konstantní velikost přírůstku Dt
(časový krok) a sledujeme, jak se rychlost za tento časový krok vlivem
zrychlení
 změní. Pro i-tý krok numerické aproximace. tak dostaneme rovnici
změní. Pro i-tý krok numerické aproximace. tak dostaneme rovnici
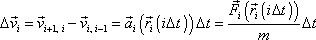 . . |
(2,33) |
V této rovnici
 značí polohový vektor bodu, v kterém se
hmotný bod (hmotnost m) dle provedené aproximace
má nacházet po proběhnutí i
časových kroků,
značí polohový vektor bodu, v kterém se
hmotný bod (hmotnost m) dle provedené aproximace
má nacházet po proběhnutí i
časových kroků,
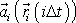 , resp.
, resp.
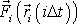 je zrychlení, resp. síla, působící
v tomto bodu. Rychlost
je zrychlení, resp. síla, působící
v tomto bodu. Rychlost
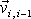 je rychlost přímočarého rovnoměrného pohybu,
kterým aproximujeme pohyb hmotného bodu v kroku, jímž dospěje do bodu
je rychlost přímočarého rovnoměrného pohybu,
kterým aproximujeme pohyb hmotného bodu v kroku, jímž dospěje do bodu
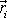 , rychlostí
, rychlostí
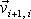 tento bod opouští. Pro polohový vektor
aproximované polohy hmotného bodu po (i+1). kroku tak dostáváme vyjádření
tento bod opouští. Pro polohový vektor
aproximované polohy hmotného bodu po (i+1). kroku tak dostáváme vyjádření
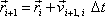 . . |
(2,34) |
Diferenci polohy
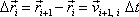 |
(2,35) |
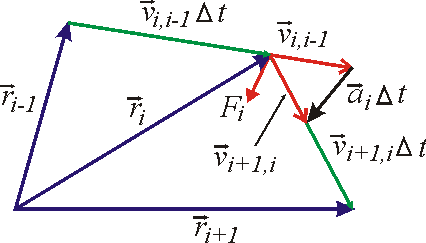 počítáme z diferenční rov-nice
(2,34)
.
Postup je ilu-strován na připojeném ná-črtku.
počítáme z diferenční rov-nice
(2,34)
.
Postup je ilu-strován na připojeném ná-črtku.
Rovnice
(2,33)
a
(2,34)
, resp.
(2,35)
nám umožní po
n krocích najít přibližnou polohu hmotného
bodu
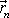 , když známe jeho polohu
, když známe jeho polohu
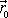 a rychlost
a rychlost
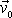 v čase
v čase
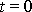 , tedy když známe počáteční podmínky jeho pohybu, a když pro každý krok známe
sílu
, tedy když známe počáteční podmínky jeho pohybu, a když pro každý krok známe
sílu
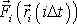 , která v daném místě v daný okamžik působí.
, která v daném místě v daný okamžik působí.
Nemusíme tedy znát celé silové pole, ale pouze sílu, která působí v daném místě v daném čase. Můžeme tedy tuto sílu změnit a tím změnit pohyb hmotného bodu. Upozorňuji čtenáře, že tato skutečnost souvisí s jedním z mírumilovným zdrojů rozvoje počítačové techniky, kterým bylo řešení problému řízených střel.
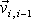 v předchozím kroku a známé síly
v místě zlomu kroků
v předchozím kroku a známé síly
v místě zlomu kroků
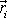 určíme dle rovnice
(2,33)
rychlost následujícího kroku;
určíme dle rovnice
(2,33)
rychlost následujícího kroku;
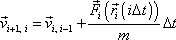 . . |
(2,36) |
Tuto rychlost dosadíme do rovnice
(2,34)
, pomocí které
najdeme předpokládanou polohu
 hmotného bodu po následujícím kroku.
Uvedeným rekurentním postupem najdeme po n
krocích (2n operacích)
polohu hmotného bodu
hmotného bodu po následujícím kroku.
Uvedeným rekurentním postupem najdeme po n
krocích (2n operacích)
polohu hmotného bodu
 v čase
v čase
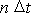 , vyjdeme-li z počátečních podmínek pohybu.
, vyjdeme-li z počátečních podmínek pohybu.
Právě popsaný postup je třeba poněkud modifikovat pro první
krok, tj. pro získání předpokládané rychlosti
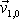 hmotného bodu v prvním kroku z počáteční rychlosti
hmotného bodu v prvním kroku z počáteční rychlosti
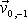 . Počáteční rychlost
. Počáteční rychlost
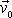 je přiřazena času
je přiřazena času
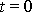 a je tedy různá od rychlosti
a je tedy různá od rychlosti
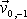 , přiřazené k času
, přiřazené k času
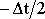 , z které by se dle výše uvedeného schématu měla rychlost
, z které by se dle výše uvedeného schématu měla rychlost
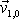 počítat. Rovnici
(2,36)
upravíme pro první krok následovně
počítat. Rovnici
(2,36)
upravíme pro první krok následovně
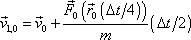 , , |
(2,37) |
zmenšíme krok na polovinu a předpokládanou lineární změnu rychlosti mezi počátkem a polovinou prvního kroku vypočteme podle hodnoty zrychlení
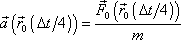 |
ve čtvrtině prvního kroku. Nelze-li tuto hodnotu ani
přibližně určit, necháme původní schéma a nahradíme v něm pro první krok
hodnotu
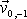 hodnotou
hodnotou
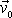 , kvalita aproximace se tím však ztrácí.
, kvalita aproximace se tím však ztrácí.
V dodatku D.4 je proveden výpočet konkrétního pohybu hmotného bodu dle právě uvedeného schématu pro případ pohybu hmotného bodu v poli elastické síly, tedy případ, který byl obecně analyticky řešen v stati 2.1.2. Proto je možno provést i porovnání přibližného numerického řešení s řešením analytickým. Je schválně volen poměrně velký krok, aby odchylky byly zřetelné. Moderní výpočetní technika (snadno dostupné vysoce výkonné počítače) umožňuje provést výpočty s obrovským počtem velmi malých kroků, jejichž výsledky jsou v jednodušších případech od analytických téměř nerozlišitelné.
Numerické řešení je důležité v těch případech, kde analytické řešení neexistuje. Jeho důležitost tkví v tom, že v aplikacích existence analytického řešení je spíše výjimkou. Proto dnes snadno dostupné velmi přesné numerické (hovorově zvané počítačové) řešení pohybových rovnic nabývá stále větší důležitosti. Důležitost počítačového řešení se netýká jen pohybových rovnic, ale velké třídy obyčejných a parciálních diferenciálních rovnic vyskytujících se ve fyzice. Z velkého množství literatury týkající se této problematiky uvádím např. [31], [32], [33], [34], [41]. V těchto knihách je možno najít, jaké problémy jsou s numerickým řešením rovnic spojeny a jaké postupy řešení se ve skutečnosti volí a jak se liší od elementárního postupu ukázaného zde.
zavři
Shrneme výsledky rozboru druhého Newtonova zákona
Známe-li trajektorii pohybu hmotného bodu v inerciální
soustavě souřadné, můžeme z druhého Newtonova zákona stanovit sílu, která
na hmotný bod působí. Ze známé pravé strany rovnice
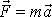 určujeme levou stranu.
určujeme levou stranu.
Známe-li silové pole v nějakém prostoru, tj. známe-li
levou stranu rovnice
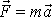 , můžeme v tomto prostoru stanovit typ pohybu hmotného bodu. Známe-li též
počáteční podmínky pohybu (případně jiné ekvivalentní údaje o pohybu), můžeme
trajektorii hmotného bodu určit jednoznačně. Zjišťujeme-li pohyb hmotného bodu
v daném silovém poli, říkáme, že řešíme pohybovou rovnici hmotného bodu.
, můžeme v tomto prostoru stanovit typ pohybu hmotného bodu. Známe-li též
počáteční podmínky pohybu (případně jiné ekvivalentní údaje o pohybu), můžeme
trajektorii hmotného bodu určit jednoznačně. Zjišťujeme-li pohyb hmotného bodu
v daném silovém poli, říkáme, že řešíme pohybovou rovnici hmotného bodu.
Pohybovou rovnici můžeme též řešit numericky. V tom případě vyjdeme z počátečních podmínek a vývoj konkrétního pohybu hmotného bodu konstruujeme postupnými kroky, v kterých uvažujeme změny rychlosti vyvolané působící silou.