Po obecném rozboru Newtonových zákonů si v tomto a následujícím článku všimneme hlavních praktických aplikací druhého Newtonova zákona. V tomto článku budeme určovat sílu, která vyvolává známý pohyb. V následujícím článku budeme hledat, jaké pohyby mohou vznikat při známém silovém působení.
Známe-li trajektorii pohybu v
inerciální soustavě souřadné,
můžeme určit síly, které v průběhu pohybu na hmotný bod působí.
Znamená to stanovit zrychlení
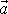 pohybu způsobem popsaným v kap.1 a pak
podle rovnice
(2,1)
, při známé hmotnosti m
pohybujícího se hmotného bodu, vypočítat sílu
pohybu způsobem popsaným v kap.1 a pak
podle rovnice
(2,1)
, při známé hmotnosti m
pohybujícího se hmotného bodu, vypočítat sílu
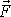 .
Příklady silových působení.
.
Příklady silových působení.
Přímočarý rovnoměrný pohyb
Z rovnice
(1,21)
plyne, že zrychlení a = 0, tedy pohyb se děje bez působení síly.
Pohyb přímočarý rovnoměrně zrychlený
Rovnice
(1,24)
udává, že zrychlení přímočarého rovnoměrně
zrychleného pohybu má stálou hodnotu
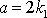 , předpokládáme-li, že pohyb je zapsán ve tvaru
(1,22)
. Tedy síla působící na
hmotný bod o hmotnosti m, který
koná rovnoměrně zrychlený přímočarý pohyb, je stálá síla
, předpokládáme-li, že pohyb je zapsán ve tvaru
(1,22)
. Tedy síla působící na
hmotný bod o hmotnosti m, který
koná rovnoměrně zrychlený přímočarý pohyb, je stálá síla
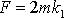 .
.
Harmonický pohyb
Vynásobíme-li rovnici
(1,33)
hmotností m
hmotného bodu, je zřejmé tvrzení: Při
harmonickém pohybu hmotného bodu působí na něj síla, jejíž velikost je úměrná výchylce
hmotného bodu z rovnovážné polohy. Síla míří vždy k rovnovážné poloze
hmotného bodu, tedy její smysl je opačný než smysl výchylky. Můžeme také říci,
že orientace síly je opačná než orientace výchylky.
Obecný přímočarý pohyb
V případě obecného přímočarého pohybu je zrychlení a
bodu obecnou funkcí času
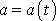 , z čehož plyne, že i síla, která působí na hmotný bod konající takový
pohyb, je obecnou funkcí času
, z čehož plyne, že i síla, která působí na hmotný bod konající takový
pohyb, je obecnou funkcí času
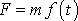 .
.
Síla
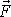 působící na hmotný bod konající obecný
přímočarý pohyb není však obecnou silou. Její směr musí být totožný se směrem
přímky, po které se hmotný bod pohybuje. Síla
působící na hmotný bod konající obecný
přímočarý pohyb není však obecnou silou. Její směr musí být totožný se směrem
přímky, po které se hmotný bod pohybuje. Síla
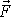 je výslednicí všech sil, které na hmotný bod
působí, tj. jak sil udržujících hmotný bod v přímce, kterým říkáme
vazbové, tak sil, které způsobují pohyb
hmotného bodu, kterým říkáme síly vtištěné nebo též hybné .
je výslednicí všech sil, které na hmotný bod
působí, tj. jak sil udržujících hmotný bod v přímce, kterým říkáme
vazbové, tak sil, které způsobují pohyb
hmotného bodu, kterým říkáme síly vtištěné nebo též hybné .
Rovnoměrný kruhový pohyb
Vyjdeme z rovnice
(1,39)
. Pro sílu
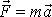 , která působí na hmotný bod o hmotnosti m
konající rovnoměrný kruhový pohyb, dostáváme vyjádření
, která působí na hmotný bod o hmotnosti m
konající rovnoměrný kruhový pohyb, dostáváme vyjádření
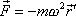 . . |
(2,3) |
Přihlédneme-li k významu symbolů, který je vysvětlen
ve stati 1.4.2, můžeme vyslovit tvrzení: Síla, která působí na hmotný bod,
který koná rovnoměrný kruhový pohyb, je síla mířící do středu kružnice. Její
velikost
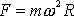 . Tuto sílu budeme nazývat silou dostředivou.
. Tuto sílu budeme nazývat silou dostředivou.
Sledujeme-li rovnoměrný kruhový pohyb hmotného bodu v inerciální soustavě souřadné, stačí silové působení na hmotný bod při rovnoměrném kruhovém pohybu plně vysvětlit silou dostředivou. O dalších silách, např. o síle odstředivé není třeba uvažovat.
Nerovnoměrný pohyb po kružnici
Při nerovnoměrném pohybu po kružnici je tečná složka
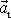 vektoru zrychlení
vektoru zrychlení
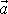 nenulová. Proto síla
nenulová. Proto síla
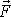 působící na hmotný bod nemíří do středu
kružnice, po které se hmotný bod pohybuje. Zrychlení
působící na hmotný bod nemíří do středu
kružnice, po které se hmotný bod pohybuje. Zrychlení
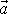 pohybu dané rovnicí
(1,44)
se rozkládá na tečnou a normálovou složku;
pohybu dané rovnicí
(1,44)
se rozkládá na tečnou a normálovou složku;
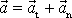 . Pro sílu
. Pro sílu
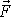 budeme psát vyjádření
budeme psát vyjádření
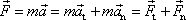 |
neboli ji rozložíme na tečnou složku
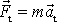 a normálovou složku
a normálovou složku
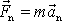 mířící do středu kružnice. Z rovnice
(1,18)
, uvědomíme-li si, že
mířící do středu kružnice. Z rovnice
(1,18)
, uvědomíme-li si, že
 , plyne pro velikost tečné složky síly
, plyne pro velikost tečné složky síly
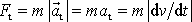 . Tečná složka síly je rovna časové změně velikosti rychlosti hmotného bodu.
Z rovnice
(1,45)
plyne, že velikost normálové složky síly je
. Tečná složka síly je rovna časové změně velikosti rychlosti hmotného bodu.
Z rovnice
(1,45)
plyne, že velikost normálové složky síly je
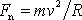 . Velikost normálové složky síly kromě velikosti rychlosti hmotného bodu závisí
též na poloměru kružnice, po které hmotný bod obíhá, roste se čtvercem
rychlosti a je nepřímo úměrná poloměru.
. Velikost normálové složky síly kromě velikosti rychlosti hmotného bodu závisí
též na poloměru kružnice, po které hmotný bod obíhá, roste se čtvercem
rychlosti a je nepřímo úměrná poloměru.
Volný pád
Experimentálně lze zjistit , že
pohyb všech volných těles vypuštěných s nulovou počáteční rychlostí
v blízkém okolí Země lze popsat rovnicí
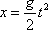 , , |
(2,4) |
když osu x volíme ve svislém směru, její kladný smysl necháme mířit k Zemi (orientujeme ji svisle dolů) a počátek volíme tak, že se v něm na počátku pohybu (v čase t = 0) nachází hmotný bod, jímž nahrazujeme těleso, jehož pohyb sledujeme. Pohyb nazýváme volným pádem. Volný pád je speciálním případem rovnoměrně zrychleného pohybu.
Důležitou experimentální
skutečností je, že zrychlení zde označené
g je pro všechny hmotné body (tělesa) v daném místě stejné.
Síla
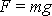 působící na hmotný bod ve směru uvažované
souřadnicové osy x
je tedy úměrná hmotnosti tělesa m.
Pro stanovení silového pole v okolí Země, které budeme
nazývat tíhovým polem, není
podstatné, že bod koná volný pád. Při každém jiném pohybu na něj v okolí
Země působí stejná síla. Tuto sílu nazýváme tíhou
(dříve se říkalo vahou) a budeme ji označovat symbolem
působící na hmotný bod ve směru uvažované
souřadnicové osy x
je tedy úměrná hmotnosti tělesa m.
Pro stanovení silového pole v okolí Země, které budeme
nazývat tíhovým polem, není
podstatné, že bod koná volný pád. Při každém jiném pohybu na něj v okolí
Země působí stejná síla. Tuto sílu nazýváme tíhou
(dříve se říkalo vahou) a budeme ji označovat symbolem
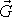 . Pro tíhu (tíhovou sílu) můžeme tedy
psát vyjádření
. Pro tíhu (tíhovou sílu) můžeme tedy
psát vyjádření
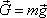 , , |
(2,5) |
kde
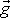 je v daném místě konstantní vektor, který nazýváme
tíhovým zrychlením, přesněji místním tíhovým zrychlením.
je v daném místě konstantní vektor, který nazýváme
tíhovým zrychlením, přesněji místním tíhovým zrychlením.
Porovnáváme-li poměr hmotností
dvou hmotných bodů (dvou těles) podle poměru velikostí tíhových sil na ně
působících, který dle
(2,5)
při konstantním
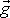 je
je
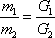 , , |
(2,6) |
říkáme, že porovnáváme jejich
tíhové hmotnosti. Porovnáváme-li hmotnosti dvou hmotných bodů (dvou těles)
podle úměry
(2,2)
, mluvíme o porovnávání setrvačných hmotností. Skutečnost, že
obě porovnání vedou ke stejným výsledkům, tj. ke stejné míře pro hmotnost
m,
je dána experimentálním faktem konstantní hodnotou tíhového zrychlení
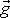 pro všechny hmotné body (tělesa) nacházející
se v jednom místě tíhového pole. Popsaná skutečnost bývá formulována jako
rovnost tíhové a setrvačné hmotnosti
. Tento z hlediska Newtonovy mechaniky
experimentální fakt je základním principem Einsteinovy obecné teorie relativity
(viz např. [27]).
pro všechny hmotné body (tělesa) nacházející
se v jednom místě tíhového pole. Popsaná skutečnost bývá formulována jako
rovnost tíhové a setrvačné hmotnosti
. Tento z hlediska Newtonovy mechaniky
experimentální fakt je základním principem Einsteinovy obecné teorie relativity
(viz např. [27]).
zavři