Rozborem Newtonových zákonů jsme ukázali, že rovnice
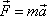 |
(2,1) |
vystihující obsah druhého Newtonova zákona platí pouze
v
inerciální soustavě souřadné
Zrychlení
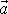 je zrychlením vůči inerciální soustavě
souřadné a jakožto veličinu úměrnou tomuto zrychlení jsme zavedli sílu (viz
stať 2.1.2). Druhým Newtonovým zákonem jsme tedy zavedli sílu jakožto veličinu
úměrnou zrychlení hmotného bodu vůči inerciální soustavě souřadné. Takové síle
budeme říkat síla pravá.
je zrychlením vůči inerciální soustavě
souřadné a jakožto veličinu úměrnou tomuto zrychlení jsme zavedli sílu (viz
stať 2.1.2). Druhým Newtonovým zákonem jsme tedy zavedli sílu jakožto veličinu
úměrnou zrychlení hmotného bodu vůči inerciální soustavě souřadné. Takové síle
budeme říkat síla pravá.
Vyšetřujeme-li pohyb hmotného bodu vůči neinerciální soustavě souřadné takovou soustavou je přísně vzato i soustava spjatá s naší Zemí ,máme dvě možnosti:
1) Vyšetřování provést v inerciální soustavě souřadné, tj. v soustavě souřadné spjaté se stálicemi a výsledky převést (transformovat) do uvažované neinerciální soustavy.
2) Formálně zachovat tvar rovnice (2,1) a přidat síly, které vykompenzují zrychlený pohyb neinerciální soustavy souřadné vůči soustavě inerciální.
První postup je pojmově bezproblémový, pracujeme pouze se standardně dle Newtonových zákonů zavedenými silami, bývá však velmi pracný. Druhý postup bývá početně jednodušší, ale vyžaduje zavedení veličin, které kompenzují zrychlený pohyb neinerciální soustavy vůči soustavě inerciální. Tyto veličiny zavedeme do rovnice
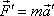 |
(2,1´) |
jako "síly", které vysvětlují rozdíl mezi zrychlením
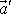 hmotného bodu vůči neinerciální soustavě
souřadné a jeho zrychlením
hmotného bodu vůči neinerciální soustavě
souřadné a jeho zrychlením
 vůči inerciální soustavě souřadné. Vůči
inerciální soustavě souřadné by takové síly nevyvolávaly žádné zrychlení a
nejsou tedy dle definice síly uvedené ve stati 2.1.2 žádnými silami. Nazýváme
je proto zdánlivé síly. Jejich původ
není možno vysvětlit fyzikálně (např. jako vliv jiných těles obklopujících
vyšetřovaný hmotný bod), jsou zavedeny pouze proto, abychom mohli i
v neinerciální soustavě souřadné užít rovnici
(2,1´)
, která má stejný tvar
jako rovnice
(2,1)
druhého Newtonova zákona. V rovnici
(2,1´)
zdánlivé
síly spolu se silami pravými vytvářejí veličinu
vůči inerciální soustavě souřadné. Vůči
inerciální soustavě souřadné by takové síly nevyvolávaly žádné zrychlení a
nejsou tedy dle definice síly uvedené ve stati 2.1.2 žádnými silami. Nazýváme
je proto zdánlivé síly. Jejich původ
není možno vysvětlit fyzikálně (např. jako vliv jiných těles obklopujících
vyšetřovaný hmotný bod), jsou zavedeny pouze proto, abychom mohli i
v neinerciální soustavě souřadné užít rovnici
(2,1´)
, která má stejný tvar
jako rovnice
(2,1)
druhého Newtonova zákona. V rovnici
(2,1´)
zdánlivé
síly spolu se silami pravými vytvářejí veličinu
 , která určuje zrychlení
, která určuje zrychlení
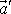 hmotného bodu o hmotnosti m
vůči neinerciální soustavě souřadné;
hmotného bodu o hmotnosti m
vůči neinerciální soustavě souřadné;
V rovnici
(2,15)
je
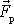 označen součet pravých sil a
označen součet pravých sil a
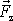 součet zdánlivých sil působících na hmotný
bod.
součet zdánlivých sil působících na hmotný
bod.
Rovnice
(2,15)
je základní rovnicí pro výpočet pohybu
hmotných bodů vůči neinerciální soustavě souřadné.
Má tvar rovnice
(2,1)
, při její aplikaci však musíme k pravým silám přidat síly zdánlivé. Ty
kompenzují zrychlený pohyb neinerciální soustavy souřadné vůči inerciální
soustavě a mají tak pro různé neinerciální soustavy různý tvar. Rovnici
(2,15)
,
která je formálně shodná s rovnicí
(2,1)
, užíváme v neinerciální
soustavě souřadné shodným způsobem jako rovnici
(2,1)
v soustavě
inerciální. Ze zjištěného zrychlení
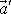 hmotného bodu vůči neinerciální soustavě můžeme určit veličinu
hmotného bodu vůči neinerciální soustavě můžeme určit veličinu
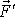 , která toto zrychlení vysvětluje. Tato veličina je součtem pravých i zdánlivých
sil, nemůže tedy sloužit k definici sil pravých, přesto ji často dle
jejího fyzikálního rozměru označujeme jako sílu. Známe-li sílu
, která toto zrychlení vysvětluje. Tato veličina je součtem pravých i zdánlivých
sil, nemůže tedy sloužit k definici sil pravých, přesto ji často dle
jejího fyzikálního rozměru označujeme jako sílu. Známe-li sílu
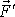 , můžeme řešením rovnice
(2,15)
najít pohyby, které v tomto silovém poli
vznikají. Formálně postupujeme zcela stejně jako při řešení rovnice
(2,1)
v inerciální soustavě souřadné, a proto rovnici
(2,15)
také označujeme jako pohybovou rovnici. Je to
pohybová rovnice pro pohyb hmotného bodu vůči neinerciální soustavě souřadné.
, můžeme řešením rovnice
(2,15)
najít pohyby, které v tomto silovém poli
vznikají. Formálně postupujeme zcela stejně jako při řešení rovnice
(2,1)
v inerciální soustavě souřadné, a proto rovnici
(2,15)
také označujeme jako pohybovou rovnici. Je to
pohybová rovnice pro pohyb hmotného bodu vůči neinerciální soustavě souřadné.
Vzhledem k tomu, že velikost zdánlivých sil závisí na vzájemném pohybu vztažných soustav, uvedeme tvary zdánlivých sil pro případ, kdy neinerciální soustava se vůči soustavě inerciální pohybuje se stálým zrychlením, a kdy se vůči inerciální soustavě otáčí stálou rychlostí. V prvém případě nazýváme zdánlivou sílu silou setrvačnou, v druhém jsou zdánlivé síly dvě: síla setrvačná a síla Coriolisova. Zvláštním případem rotující soustavy je i naše Země.
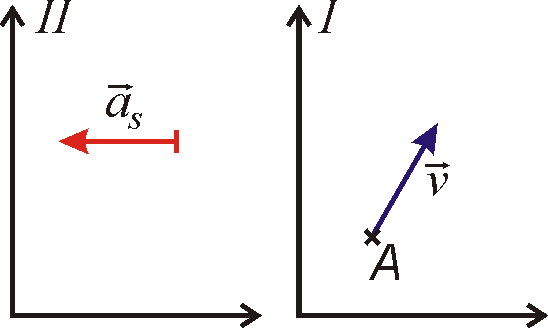 Mějme dvě soustavy souřadné, z nichž jedna se vůči druhé pohybuje se zrychlením
Mějme dvě soustavy souřadné, z nichž jedna se vůči druhé pohybuje se zrychlením
 , tedy situaci znázorněnou na obr.6, který zde překreslujeme. Budeme
předpokládat, že soustava I je inerciální a bod A se vůči ní pohybuje
s konstantní rychlostí
, tedy situaci znázorněnou na obr.6, který zde překreslujeme. Budeme
předpokládat, že soustava I je inerciální a bod A se vůči ní pohybuje
s konstantní rychlostí
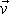 , neboli koná vůči soustavě I rovnoměrný přímočarý pohyb. Soustava II se pohybuje
vůči inerciální soustavě I zrychleným pohybem s nenulovým konstantním
zrychlením
, neboli koná vůči soustavě I rovnoměrný přímočarý pohyb. Soustava II se pohybuje
vůči inerciální soustavě I zrychleným pohybem s nenulovým konstantním
zrychlením
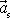 , a tedy soustava II je neinerciální. Předpoklad o konstantním vzájemném
zrychlení soustav znamená, že soustavy se vůči sobě neotáčí.
, a tedy soustava II je neinerciální. Předpoklad o konstantním vzájemném
zrychlení soustav znamená, že soustavy se vůči sobě neotáčí.
Pohyb bodu A vůči neinerciální soustavě II je pohybem
s konstantním zrychlením
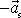 . Jelikož hmotný bod A koná vůči inerciální soustavě souřadné rovnoměrný
přímočarý pohyb, žádná pravá síla na něj nepůsobí. Zrychlený pohyb se zrychlením
. Jelikož hmotný bod A koná vůči inerciální soustavě souřadné rovnoměrný
přímočarý pohyb, žádná pravá síla na něj nepůsobí. Zrychlený pohyb se zrychlením
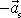 hmotného bodu A o hmotnosti m
vůči neinerciální soustavě souřadné II
vysvětlíme zavedením zdánlivé síly
hmotného bodu A o hmotnosti m
vůči neinerciální soustavě souřadné II
vysvětlíme zavedením zdánlivé síly
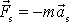 . Síla
. Síla
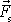 kompenzuje zrychlený pohyb, který koná
soustava II vůči inerciální soustavě I. Pohybová rovnice
(2,15)
pro pohyb
hmotného bodu vůči soustavě II má vzhledem k tomu, že žádná pravá síla
nepůsobí, tvar
kompenzuje zrychlený pohyb, který koná
soustava II vůči inerciální soustavě I. Pohybová rovnice
(2,15)
pro pohyb
hmotného bodu vůči soustavě II má vzhledem k tomu, že žádná pravá síla
nepůsobí, tvar
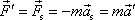 . . |
Protože předpokládáme, že zrychlení
 , a tedy i setrvačná síla
, a tedy i setrvačná síla
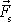 jsou konstantní, je pohybová rovnice
jsou konstantní, je pohybová rovnice
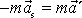 formálně shodná s rovnicí
(2,7)
. Hmotný
bod se vůči neinerciální soustavě souřadné II pohybuje s konstantním
zrychlením
formálně shodná s rovnicí
(2,7)
. Hmotný
bod se vůči neinerciální soustavě souřadné II pohybuje s konstantním
zrychlením
 , koná tedy vůči ní vrhy , v kterých tíhové zrychlení
, koná tedy vůči ní vrhy , v kterých tíhové zrychlení
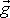 je nahrazeno zrychlením
je nahrazeno zrychlením
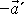 .
.
Když obě uvažované soustavy souřadné I a II vložíme do
tíhového silového pole
(2,5)
, začne na hmotný bod působit pravá síla tíha
hmotného bodu
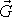 . Hmotný bod pak vůči inerciální soustavě souřadné I koná pohyb odpovídající
pohybové rovnici
(2,7)
. Hmotný bod pak vůči inerciální soustavě souřadné I koná pohyb odpovídající
pohybové rovnici
(2,7)
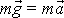 , tedy některý z vrhů. Pohybová rovnice pro pohyb hmotného bodu vůči neinerciální
soustavě souřadné má nyní tvar
, tedy některý z vrhů. Pohybová rovnice pro pohyb hmotného bodu vůči neinerciální
soustavě souřadné má nyní tvar
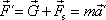 , , |
(2,16) |
neboli po rozepsání výrazů pro
 ,
,
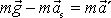 . Znovu na levé straně rovnice je konstantní vektor, a tedy i v tomto
případě bude hmotný bod vůči neinerciální soustavě II konat vrhy . Tentokrát
v těchto zobecněných vrzích bude tíhové zrychlení
. Znovu na levé straně rovnice je konstantní vektor, a tedy i v tomto
případě bude hmotný bod vůči neinerciální soustavě II konat vrhy . Tentokrát
v těchto zobecněných vrzích bude tíhové zrychlení
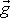 nahrazeno zrychlením
nahrazeno zrychlením
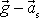 . Hmotný bod se bude vůči neinerciální soustavě souřadné II pohybovat po
parabolické dráze, kde osa paraboly bude ležet ve směru daném vektorem
. Hmotný bod se bude vůči neinerciální soustavě souřadné II pohybovat po
parabolické dráze, kde osa paraboly bude ležet ve směru daném vektorem
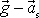 a její orientace bude shodné
s orientací tohoto vektoru.
a její orientace bude shodné
s orientací tohoto vektoru.
Podobně jako v předcházejícím případě budeme i zde hledat zdánlivé síly, které umožní sestavit pohybovou rovnici (2,15) . Nyní však úloha bude po formální stránce podstatně obtížnější.
Předpokládáme, že souřadná soustava II
se otáčí stálou úhlovou rychlostí w
vůči inerciální soustavě souřadné I.
Soustava souřadná II je tedy neinerciální. Kartézské souřadnicové soustavy
zavedeme tak, že jejich počátky a třetí osy budou splývat. Třetí osy leží
v ose otáčení. Transformační rovnice pro vztah mezi souřadnicemi
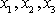 libovolného bodu v inerciální soustavě
I a souřadnicemi
libovolného bodu v inerciální soustavě
I a souřadnicemi
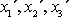 téhož bodu v neinerciální soustavě II
budou pak dány rovnicemi
téhož bodu v neinerciální soustavě II
budou pak dány rovnicemi
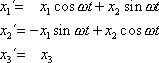 , , |
(2,17) |
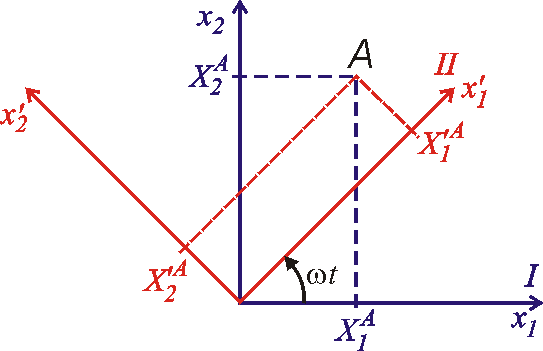 jak lze vyčíst
použitím jednoduchých trigonometrických vztahů z obr.7. Obr.7 je pohledem
proti kladném smyslu (kladné orientaci) os
jak lze vyčíst
použitím jednoduchých trigonometrických vztahů z obr.7. Obr.7 je pohledem
proti kladném smyslu (kladné orientaci) os
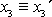 .
.
Předpokládáme, že v čase
 obě souřadnicové soustavy splývají.
Trans-formační rovnice
(2,17)
platí nejen pro souřadnice bodů, ale i pro složky
libo-volného vektoru
obě souřadnicové soustavy splývají.
Trans-formační rovnice
(2,17)
platí nejen pro souřadnice bodů, ale i pro složky
libo-volného vektoru
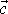 . Má-li tento vektor v soustavě I složky
. Má-li tento vektor v soustavě I složky
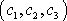 , jsou složky
, jsou složky
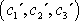 téhož vektoru v soustavě II dány výrazy
téhož vektoru v soustavě II dány výrazy
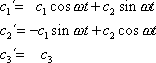 |
(2,17´) |
Mějme nyní hmotný bod, jehož pohyb vůči inerciální soustavě souřadné I je dán parametrickými rovnicemi
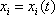 . . |
Parametrické rovnice
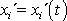 pohybu tohoto bodu vůči neinerciální
soustavě II přímým dosazením parametrických rovnic
pohybu tohoto bodu vůči neinerciální
soustavě II přímým dosazením parametrických rovnic
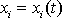 do transformačních rovnic
(2,17)
;
do transformačních rovnic
(2,17)
;
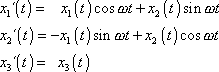 . . |
(2,18) |
Složky vektoru rychlosti
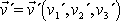 bodu vůči neinerciální soustavě II získáme
derivací právě uvedených rovnic;
bodu vůči neinerciální soustavě II získáme
derivací právě uvedených rovnic;
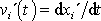 . Provedeme naznačené derivace a rovnice rozepíšeme:
. Provedeme naznačené derivace a rovnice rozepíšeme:
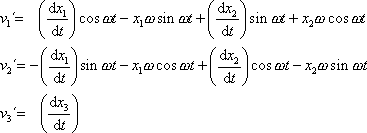 . . |
Uvědomíme-li si, že dle
(2,18)
SETEQS2('knihI22do_soubory/eq0036M.gif','knihI22do_soubory/eq0037M.gif','',',
',',','1','0.3);
můžeme výrazy pro složky vektoru
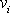 přepsat na tvar
přepsat na tvar
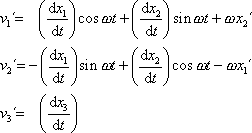 . . |
(2,19) |
Pro zrychlení
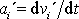 bodu vůči neinerciální soustavě II pak
derivací posledních rovnic dostáváme:
bodu vůči neinerciální soustavě II pak
derivací posledních rovnic dostáváme:
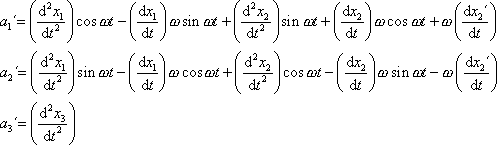 . . |
Výrazy pro zrychlení
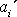 dále upravíme použitím vztahů
dále upravíme použitím vztahů
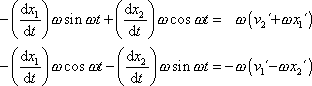 , , |
které plynou z (2,19) na tvar
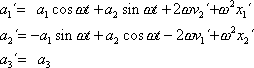 . . |
(2,20) |
V rovnicích
(2,20)
jsme složky zrychlení
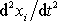 hmotného bodu vůči inerciální soustavě
souřadné I označili
hmotného bodu vůči inerciální soustavě
souřadné I označili
 a složky rychlosti
a složky rychlosti
 hmotného bodu vůči neinerciální soustavě
souřadné II
hmotného bodu vůči neinerciální soustavě
souřadné II
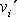 . Vynásobíme-li rovnice
(2,20)
hmotností m
hmotného bodu, dostaneme pro složky síly
. Vynásobíme-li rovnice
(2,20)
hmotností m
hmotného bodu, dostaneme pro složky síly
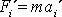 , pomocí které vysvětlíme pohyb hmotného bodu vůči neinerciální soustavě
souřadné II, vyjádření
, pomocí které vysvětlíme pohyb hmotného bodu vůči neinerciální soustavě
souřadné II, vyjádření
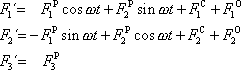 . . |
(2,21) |
V rovnici
(2,21)
jsou
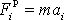 složky výsledné pravé síly (tj. součtu všech
sil fyzikálního charakteru), která působí na hmotný bod. Zrychlení
složky výsledné pravé síly (tj. součtu všech
sil fyzikálního charakteru), která působí na hmotný bod. Zrychlení
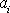 je zrychlení vůči inerciální soustavě
souřadné I. První část rovnic
(2,21)
představuje prostou geometrickou
transformaci složek pravé síly do neinerciální soustavy souřadné II dle
transformačních rovnic
(2,17´)
. Kdyby žádná pravá síla
je zrychlení vůči inerciální soustavě
souřadné I. První část rovnic
(2,21)
představuje prostou geometrickou
transformaci složek pravé síly do neinerciální soustavy souřadné II dle
transformačních rovnic
(2,17´)
. Kdyby žádná pravá síla
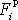 na hmotný bod nepůsobila (vůči inerciální
soustavě souřadné by se hmotný bod pohyboval rovnoměrně přímočaře nebo by vůči
ní byl v klidu), byly by nulové i její složky
na hmotný bod nepůsobila (vůči inerciální
soustavě souřadné by se hmotný bod pohyboval rovnoměrně přímočaře nebo by vůči
ní byl v klidu), byly by nulové i její složky
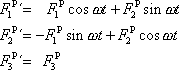 |
v neinerciální soustavě souřadné. Výrazy
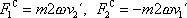 |
a
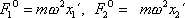 |
jsou složkami dvou zdánlivých sil
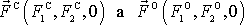 , které musíme přidat k pravé síle, abychom vysvětlili pohyb hmotného bodu
vůči neinerciální soustavě souřadné II, chceme-li v této soustavě zachovat
platnost rovnice formálně shodné s rovnicí
(2,1)
, které musíme přidat k pravé síle, abychom vysvětlili pohyb hmotného bodu
vůči neinerciální soustavě souřadné II, chceme-li v této soustavě zachovat
platnost rovnice formálně shodné s rovnicí
(2,1)
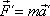 . . |
(2,22) |
V rovnici
(2,22)
pro pohyb hmotného bodu
v soustavě souřadné, která se otáčí konstantní rychlostí vůči inerciální
soustavě souřadné, se tedy síla
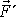 skládá z pravé síly
skládá z pravé síly
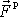 a dvou zdánlivých sil
a dvou zdánlivých sil
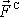 a
a
 ;
;
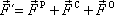 . . |
(2,23) |
Síla
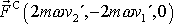 se nazývá silou Coriolisovou
a síla
se nazývá silou Coriolisovou
a síla
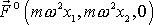 silou odstředivou.
silou odstředivou.
Síla Coriolisova a síla odstředivá jsou dvě zdánlivé síly,
které je třeba přidat k silám pravým, aby v neinerciální soustavě
souřadné, která se vůči inerciální soustavě souřadné otáčí konstantní úhlovou
rychlostí w
, bylo možno užívat pohybovou rovnici v tvaru
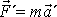 .
.
Síla odstředivá působí na všechny
hmotné body neinerciální soustavy II kromě těch, které leží na ose otáčení
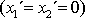 . Vektor síly leží v kolmici vedené z působiště síly na osu otáčení a
je orientován (míří) směrem od osy. Říkáme, že odstředivá síla je radiální.
Její velikost je
. Vektor síly leží v kolmici vedené z působiště síly na osu otáčení a
je orientován (míří) směrem od osy. Říkáme, že odstředivá síla je radiální.
Její velikost je
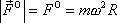 , , |
kde R je vzdálenost působiště síly od osy otáčení. Velikost odstředivé síly je shodná s velikostí dostředivé síly (2,3) . Tím však analogie mezi oběma silami končí. Dostředivá síla je síla, která působí na hmotný bod, který koná rovnoměrný kruhový pohyb. Odstředivá síla je zdánlivá síla, která působí v neinerciální soustavě souřadné, která se rovnoměrně otáčí vůči inerciální soustavě souřadné.
Odstředivou sílu nelze zapsat ve vektorovém tvaru , kde by byl polohový vektor působiště síly v neinerciální soustavě. Takové vyjádření by kromě bodů v rovině mělo nenulovou třetí složku; síla by byla centrální a ne radiální. Vyjádření lze užít pouze v rovině a v jiných rovinách kolmých k ose otáčení pouze, když do nich posuneme počátek souřadnicové soustavy.
Coriolisova síla působí pouze na hmotné body, které se vůči
neinerciální soustavě II pohybují nenulovou rychlostí
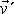 , jejíž směr není shodný se směrem osy otáčení (alespoň jedna ze složek
, jejíž směr není shodný se směrem osy otáčení (alespoň jedna ze složek
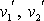 vektoru rychlosti je nenulová). Výraz pro
Coriolisovu sílu je možno zapsat ve tvaru vektorového součinu
vektoru rychlosti je nenulová). Výraz pro
Coriolisovu sílu je možno zapsat ve tvaru vektorového součinu
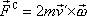 , , |
(2,24) |
kde vektorem úhlové rychlosti
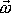 rozumíme vektor, jehož velikost je rovna
velikosti úhlové rychlosti otáčení w
, směr je směrem osy otáčení a orientace je taková,
že při pohledu v jejím smyslu se otáčení soustavy II vůči soustavě I děje
ve smyslu oběhu hodinových ručiček. V souřadnicové soustavě II i I bude
mít vektor
rozumíme vektor, jehož velikost je rovna
velikosti úhlové rychlosti otáčení w
, směr je směrem osy otáčení a orientace je taková,
že při pohledu v jejím smyslu se otáčení soustavy II vůči soustavě I děje
ve smyslu oběhu hodinových ručiček. V souřadnicové soustavě II i I bude
mít vektor
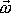 složky
složky
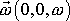 . Vypočteme-li podle pravidel o vektorovém násobení složky vektoru
(2,24)
,
zjistíme, že
. Vypočteme-li podle pravidel o vektorovém násobení složky vektoru
(2,24)
,
zjistíme, že
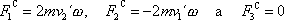 |
ve shodě s původním zavedením Coriolisovy síly.
Sledujeme-li podrobně pohyby hmotných bodů vůči Zemi,
zjistíme, že je lze přesně vysvětlit, jen když k pravým silám (gravitace,
odporové síly, elektrické síly apod.) přidáme sílu Coriolisovu a odstředivou
s hodnotou úhlové rychlosti w
rovnou
rychlosti otáčení Země vůči stálicím. Případ početně rozebraný
v předcházející stati dostaneme přesně, když soustavu souřadnou spjatou se
Zemí volíme tak, že třetí osa má směr zemské rotační osy, její kladný smysl
míří k severu a velikost úhlové rychlosti volíme rovnu rychlosti otáčení
Země vůči stálicím, tj.
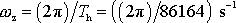 .
.
Ve výrazu pro úhlovou rychlost je doba trvání hvězdného (siderického) dne. Tento den je přibližně o čtyři minuty a čtyři sekundy kratší než sluneční (občanský) den, jehož doba trvání je .
Skutečnost, že pohyby hmotných bodů na povrchu Země lze
vysvětlit, předpokládáme-li, že Země se otáčí úhlovou rychlostí
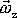 vůči inerciální soustavě souřadné, je
hlavním důvodem, proč soustavu souřadnou spjatou se stálicemi považujeme za
soustavu inerciální. Soustava spjatá se Zemí je tedy zřejmě neinerciální.
Velikost úhlové rychlosti
vůči inerciální soustavě souřadné, je
hlavním důvodem, proč soustavu souřadnou spjatou se stálicemi považujeme za
soustavu inerciální. Soustava spjatá se Zemí je tedy zřejmě neinerciální.
Velikost úhlové rychlosti
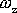 je malá, a proto i hodnoty Coriolisovy a
odstředivé síly pro pohyby v soustavě souřadné spjaté se Zemí jsou malé.
To znamená jednak, že při vyšetřování většiny běžných pohybů na Zemi lze tyto
síly zanedbat, za druhé však, že experimentální ověření jejich vlivu na pohyby
hmotných bodů vůči Zemi není snadné.
je malá, a proto i hodnoty Coriolisovy a
odstředivé síly pro pohyby v soustavě souřadné spjaté se Zemí jsou malé.
To znamená jednak, že při vyšetřování většiny běžných pohybů na Zemi lze tyto
síly zanedbat, za druhé však, že experimentální ověření jejich vlivu na pohyby
hmotných bodů vůči Zemi není snadné.
Nejprůkaznějším pokusem, který ukazuje, že soustava souřadná spjatá se Zemí je neinerciální, je pokus s Foucoultovým kyvadlem. Foucoultovo kyvadlo je těžká koule zavěšená na dlouhém závěsu, kterou necháme kývat s poměrně velkou amplitudou. Ukazuje se, že rovina kyvu takového kyvadla se vůči podlaze, tj. soustavě souřadné spjaté se Zemí, otáčí úhlovou rychlostí
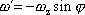 , , |
(2,25) |
kde j je
zeměpisná šířka místa, v kterém pokus provádíme. Pro názor nejjednodušší
(experimentálně ne) je provádět pokus na zemském pólu. Potom
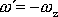 , rovina kyvu vůči podlaze se otáčí opačnou úhlovou než s jakou se otáčí
Země vůči stálicím, a tedy zřejmě kyvadlo zachovává rovinu kyvu vůči stálicím a
ne vůči Zemi. Kyvadlo zachovává rovinu kyvu v inerciální soustavě, a tedy
soustava spjatá se stálicemi je inerciální a soustava spjatá se Zemí
neinerciální.
, rovina kyvu vůči podlaze se otáčí opačnou úhlovou než s jakou se otáčí
Země vůči stálicím, a tedy zřejmě kyvadlo zachovává rovinu kyvu vůči stálicím a
ne vůči Zemi. Kyvadlo zachovává rovinu kyvu v inerciální soustavě, a tedy
soustava spjatá se stálicemi je inerciální a soustava spjatá se Zemí
neinerciální.
Násobení
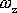 výrazem
výrazem
 v rovnici
(2,25)
odpovídá tomu, že
soustava souřadná, která má osy
v rovnici
(2,25)
odpovídá tomu, že
soustava souřadná, která má osy
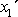 a
a
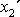 ve vodorovné rovině (podlaze) v místě
na Zemi různém od pólů, není soustavou s třetí osou v ose rotace
Země, jaká je uvažována na začátku této stati. Proto také, provedeme-li pokus
s Foucoultovým kyvadlem např. v Praze (
ve vodorovné rovině (podlaze) v místě
na Zemi různém od pólů, není soustavou s třetí osou v ose rotace
Země, jaká je uvažována na začátku této stati. Proto také, provedeme-li pokus
s Foucoultovým kyvadlem např. v Praze (
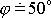 ), doba, za kterou rovina kyvu kyvadla oběhne
jednou dokola není přibližně 24 hodin jako na pólu, ale je delší, činí
přibližně 31 hodin. Na rovníku se pokus nedá uskutečnit.
), doba, za kterou rovina kyvu kyvadla oběhne
jednou dokola není přibližně 24 hodin jako na pólu, ale je delší, činí
přibližně 31 hodin. Na rovníku se pokus nedá uskutečnit.
Původní pokus konal Foucoult roku 1851 v pařížském Pantheonu s koulí hmotnosti 30 kg, kterou měl zavěšenu na závěsu délky 67 m. Relativní přesnost měření úhlové rychlosti otáčení roviny kyvu byla přibližně 0,5%. Pokus byl později mnohokrát opakován. Je např. instalován v budově OSN v New Yorku. Dlouhý závěs a těžká koule jsou při Foucoultově pokusu voleny pro omezení vnějších náhodných vlivů působících na kyvadlo. S menší koulí a kratším závěsem je měřitelné stáčení roviny kyvu Foucoultova kyvadla během 10 minut ukazováno při přednáškách na naší Matematicko-fyzikální fakultě KU.
Výklad pohybu Foucoultova kyvadla jsme provedli tak, že jsme pohyb vysvětlili jako jednoduché kývání se zachovanou rovinou kyvu v soustavě souřadné spjaté se stálicemi. Tedy převedením do inerciální soustavy, tj.způsobem označeným 1) v úvodu čl. 2.4. Kdybychom užili způsobu tam označeného 2), museli bychom stáčení roviny kyvu v neinerciální soustavě souřadné spjaté se Zemí vysvětlit zdánlivou silou působící na hmotný bod kolmo k rovině kyvu. Touto silou je síla Coriolisova. Při kývání se hmotný bod pohybuje nenulovou rychlostí a Coriolisova síla na něj zřejmě působí. Při pohybu Foucoultova kyvadla však její vliv je tak malý, že ho nepozorujeme jako zřetelné zakřivení roviny kyvu (přesněji plochy kyvu) v průběhu jednoho kyvu, ale pouze jako zřetelné stáčení roviny kyvadla za dobu několika kmitů. Provedeme-li však pokus tak, že kyvadlo umístíme na otáčející se točnu, bude vliv nyní velké Coriolisovy síly naprosto zřetelný. Plochy kyvu se silně zkřiví a průmět koncového bodu kyvadla na rovinu kolmou k ose otáčení vykreslí pěknou kytičku. Při tomto pokusu pokládáme soustavu souřadnou spjatou se Zemí za inerciální (zanedbáme její výše vyšetřovanou slabou neinercionálnost) a vykreslení kytičky zprostředkujeme barevnou kapalinou vytékající z kyvadla.
Odstředivá síla se nejzřetelněji projeví závislostí hodnoty tíhového zrychlení g na zeměpisné šířce místa, kde jej sledujeme. Velikost místního tíhového zrychlení vzrůstá od rovníku k pólu, přičemž rozdíl hodnot činí asi 0,5% hodnoty g. Tento rozdíl je zanedbatelný jen při hrubých měřeních. Tíha (váha) tělesa závisí na místě, kde ji zjišťujeme. Proto je nyní na zboží vždy udávána jeho hmotnost a ne váha. Pro přepočet jednotek dříve užívané technické soustavy jednotek, kde základní jednotkou byl kilopond, tj. síla, kterou je hmotnost jednoho kilogramu přitahována k Zemi, na jednotky SI (srovnej dodatek D.2) se užívá standardní hodnota tíhového zrychlení nazývaná normální zrychlení volného pádu (též normální tíhové zrychlení)
Pozor se záměnou se stejně označenou funkcí, kterou geofyzikové popisují hodnoty tíhového zrychlení v různých místech zidealizovaného modelu zemského elipsoidu.
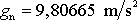 (přesně). Tato hodnota je přibližně rovna
místnímu tíhovému zrychlení na
(přesně). Tato hodnota je přibližně rovna
místnímu tíhovému zrychlení na
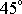 zeměpisné šířky při mořské hladině. Často
uvažovaná hodnota tíhového zrychlení
zeměpisné šířky při mořské hladině. Často
uvažovaná hodnota tíhového zrychlení
 dobře odpovídá hodnotě tíhového zrychlení
v Praze.
dobře odpovídá hodnotě tíhového zrychlení
v Praze.
Podstatný vliv na změny tíhového zrychlení se zeměpisnou
šířkou místa, kde jej sledujeme, má odstředivá síla, tj. zdánlivá síla
vysvětlující pohyby vůči soustavě souřadné spjaté se Zemí, která je
neinerciální souřadnou soustavou. Abychom tento vliv vysvětlili, budeme
uvažovat hmotný bod, který je v klidu vůči Zemi a na nějž působí
z pravých sil pouze gravitační síla
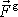 . Kromě gravitační síly, která je vyvolána působením hmotnosti Země, působí na
takový hmotný bod, když jej sledujeme ze Země, ještě zdánlivá síla síla
odstředivá
. Kromě gravitační síly, která je vyvolána působením hmotnosti Země, působí na
takový hmotný bod, když jej sledujeme ze Země, ještě zdánlivá síla síla
odstředivá
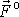 . Tyto síly spolu s výslednou silou
. Tyto síly spolu s výslednou silou
 |
(2,26) |
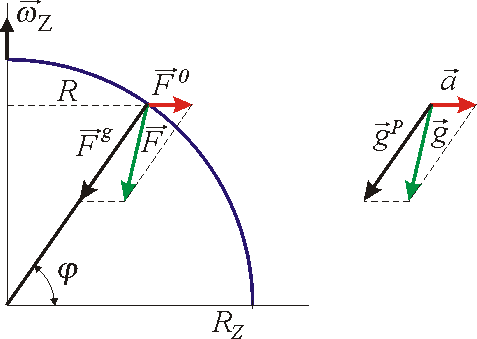 působící na hmotný bod m,
který se nachází v místě o zeměpisné šířce j
, jsou znázorněny na obr.8. Výsledná síla
působící na hmotný bod m,
který se nachází v místě o zeměpisné šířce j
, jsou znázorněny na obr.8. Výsledná síla
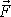 , která působí na hmotný bod, odpovídá jeho tíze v daném místě,
, která působí na hmotný bod, odpovídá jeho tíze v daném místě,
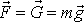 . Síla
. Síla
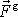 je síla působící na hmotný bod dle
všeobecného gravitačního záko-na
(4,1)
;
je síla působící na hmotný bod dle
všeobecného gravitačního záko-na
(4,1)
;
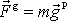 , kde
, kde
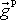 jsme označili zrychlení bodu způsobené
hmotností Země. Odstředivá síla způsobená rotací Země vůči inerciální soustavě
souřadná je
jsme označili zrychlení bodu způsobené
hmotností Země. Odstředivá síla způsobená rotací Země vůči inerciální soustavě
souřadná je
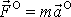 a pro její velikost dostáváme:
a pro její velikost dostáváme:
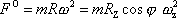 |
V posledních rovnicích jsme uži-li označení
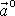 pro odstředivé zrychlení a
pro odstředivé zrychlení a
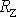 pro poloměr Země. Z rovnice
(2,26)
plyne vztah mezi zrychleními
pro poloměr Země. Z rovnice
(2,26)
plyne vztah mezi zrychleními
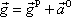 , , |
(2,27) |
která odpovídají silám
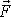 ,
,
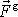 a
a
 . Rovnice
(2,27)
(viz též obr.8 b))
ukazuje, že experimentálně zjištěné tíhové zrychlení
. Rovnice
(2,27)
(viz též obr.8 b))
ukazuje, že experimentálně zjištěné tíhové zrychlení
 v daném místě zemského povrchu je
vektorovým součtem skutečného, tj. hmotností Země vyvolaného gravitačního
zrychlení
v daném místě zemského povrchu je
vektorovým součtem skutečného, tj. hmotností Země vyvolaného gravitačního
zrychlení
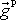 a odstředivého zrychlení
a odstředivého zrychlení
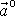 .
.
Rovnice
(2,27)
vysvětluje různou hodnotu tíhového
zrychlení
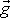 v různých místech zemského povrchu.
Z rovnice
(2,27)
plyne užitím kosinové věty pro velikost tíhového
zrychlení g
v zeměpisné
šířce j
vyjádření
v různých místech zemského povrchu.
Z rovnice
(2,27)
plyne užitím kosinové věty pro velikost tíhového
zrychlení g
v zeměpisné
šířce j
vyjádření
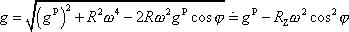 . . |
Na pólu
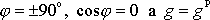 , což ovšem plyne již přímo z
(2,27)
, neboť na pólech
, což ovšem plyne již přímo z
(2,27)
, neboť na pólech
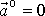 . Hodnotu tíhového zrychlení g
na pólech označíme
. Hodnotu tíhového zrychlení g
na pólech označíme
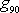 . Na rovníku je zeměpisná šířka
. Na rovníku je zeměpisná šířka
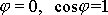 a pro tíhové zrychlení, které označíme
a pro tíhové zrychlení, které označíme
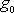 , dostáváme vyjádření
, dostáváme vyjádření
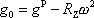 ; ; |
zrychlení gravitační
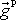 a zrychlení odstředivé
a zrychlení odstředivé
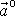 na rovníku míří proti sobě. Rozdíl
zrychlení
na rovníku míří proti sobě. Rozdíl
zrychlení
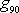 na pólu a zrychlení
na pólu a zrychlení
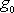 na rovníku má tedy být
na rovníku má tedy být
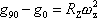 . . |
(2,28) |
Dosadíme-li číselné hodnoty
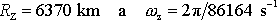 , dostaneme po zaokrouhlení
, dostaneme po zaokrouhlení
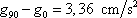 . . |
(2,29) |
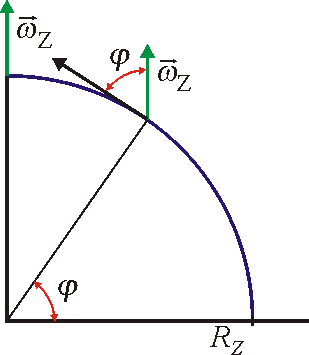 Tato hodnota je však
menší než experimentálně zjištěný rozdíl tíhového zrychlení na pólech a na
rovníku, který činí přibližně
Tato hodnota je však
menší než experimentálně zjištěný rozdíl tíhového zrychlení na pólech a na
rovníku, který činí přibližně
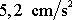 . Nesouhlas hodnoty
. Nesouhlas hodnoty
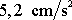 s hodnotou
(2,29)
se vysvětluje tím, že
vzdálenost pólů od středu Země je menší než vzdálenost bodů na rovníku od
středu Země, tedy sploštěním Země.
s hodnotou
(2,29)
se vysvětluje tím, že
vzdálenost pólů od středu Země je menší než vzdálenost bodů na rovníku od
středu Země, tedy sploštěním Země.
Dalšími projevy toho, že soustavy souřadné spjaté se Zemí
nejsou inerciální, jsou projevy Coriolisovy síly na pravidelné pohyby na
zemském povrchu a v atmosféře. Pohybuje-li se na severní polokouli hmotný
bod od jihu k severu, působí na něj Coriolisova síla východním směrem.
Plyne to z rovnice
(2,24)
a pro názornost je připojen obr.9, na němž je
znázorněna rychlost
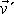 bodu, úhlová rychlost rotace Země
bodu, úhlová rychlost rotace Země
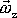 a zeměpisná šířka j
místa, v kterém se hmotný bod nachází.
Např. pro hmotný bod hmotnosti
a zeměpisná šířka j
místa, v kterém se hmotný bod nachází.
Např. pro hmotný bod hmotnosti
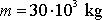 , který se pohybuje rychlostí 50 km/hod,
je velikost této síly na 50o
severní šířky
, který se pohybuje rychlostí 50 km/hod,
je velikost této síly na 50o
severní šířky
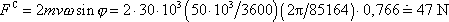 . . |
Tedy na třicetitunový vagón pohybující se v udaném
místě rychlostí 50 km/hod po kolejích jedoucích od jihu k severu
působí Coriolisova síla velikosti
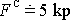 .
.
Užili jsme úmyslně pro názornost jednotku technické soustavy kilopond (kp), zvanou též kilogram tíhový; 1 kp =9,80665 N. Takto můžeme říct, že v uvažovaném případě z 30 tun tíhy vagónu 5 kg působí kolmo jako Coriolisova síla směrem na východ.
Uvádí se, že při jednosměrném provozu na železničních tratích severojižního směru lze pozorovat větší opotřebení té koleje, ke které míří Coriolisova síla. Taková pozorování se např. konala na velmi frekventované dvoukolejné trati z Břeclavi do Přerova v druhé polovině 19. století. Podobně se uvádí, že u řek tekoucích na severní polokouli od jihu k severu takovými jsou např. sibiřské řeky , lze pozorovat větší vymílání pravého než levého břehu. Působením Coriolisovy síly lze vysvětlit i stáčení ze severojižního směru pravidelných větrů pasátů vanoucích v tropických oblastech a opačný smysl rotace vzdušných vírů cyklónů na severní a jižní polokouli.
Na závěr této stati bych chtěl znovu zdůraznit, že při vyšetřování většiny pohybů na povrchu Země nemusíme zdánlivé síly uvažovat. Buď jsou tak malé, že je můžeme zanedbat nebo jejich působení není pro popis pohybů podstatné. Např. při výpočtu spotřeby paliva lokomotivy vezoucí výše uvedený třicetitunový vagón určitě zanedbáme tření vyvolané Coriolisovou silou. Druhý případ nastane např. při sledování vrhů. Počítáme-li, jak daleko koulař vrhne své náčiní, není pro nás podstatné, že působením odstředivé síly kolmice nemíří do středu Země. Při většině praktických aplikací Newtonovy mechaniky můžeme pokládat soustavu souřadnou spjatou se Zemí za soustavu inerciální, odchylky jsou buď zanedbatelné nebo pro řešení problému nepodstatné.