 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Při pohybu tekutin se jejich deformace mění s časem.
Příklad pohybu, při kterém se deformace neustále mění, jsme probrali v čl.
1.3, kde jsme též ukázali, že k popisu takového pohybu je vhodnější užít
tenzor rychlosti deformace
než tenzor deformace
.
V předešlém studiu [2] jste podrobněji probrali model dokonalé kapaliny a
dokonalého plynu. O dokonalé kapalině se předpokládá, že je nestlačitelná, o
dokonalém plynu, že je stlačitelný a pro obě dokonalé tekutiny se předpokládá
nulová viskozita. V [2] se
viskozita nazývá vnitřním třením a není blíže určená. Co budeme viskozitou
přesně rozumět, vysvětlíme dále v tomto článku.
Představa dokonalé tekutiny je vhodná k popisu základních mechanických jevů v tekutinách. Podrobněji se tímto modelem budeme zabývat v kap .4 a 5. Podobně jako model tuhého tělesa probraný v I ani modely dokonalých tekutin neberou v úvahu materiálové zvláštnosti látek. V rovnicích odvozených na jejich základě se vyskytuje jen celková hmotnost tělesa nebo hustota látky. Materiálové konstanty určující deformační chování látek chybí. Proto model tuhého tělesa a modely dokonalých tekutin obvykle do reologické klasifikace látek nezařazujeme[*]. Reologicky jsou z modelů tekutin zajímavé až ty, které uvažují nenulovou viskozitu reálných látek. Mluvíme o viskózních látkách. Většina viskózních látek jsou tekutiny a z nich výraznější viskózní vlastnosti mají kapaliny. Proto se pro viskózní látky užívá též názvů viskózní tekutiny a viskózní kapaliny.
Nejjednodušším předpokladem o vlivu viskozity na proudění
tekutiny je předpoklad o přímé úměrnosti mezi libovolnou složkou
deviátoru rychlosti deformace a odpovídající
složkou
deviátoru napětí (viz
(2,24)
)
 . |
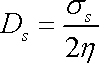(2,47) |
Rovnice
(2,47)
, jejíž tvar je analogický rovnici
(2,42)
, se
nazývá Newtonovým zákonem pro proudění viskózní tekutiny nebo stručně Newtonův viskózní zákon. Tato rovnice
je charakteristickou reologickou rovnicí newtonovské
látky. Konstantu h vystihující
viskózní vlastnosti tekutiny nazýváme viskozita.
Pro odlišení od výrazu
nazývaného kinematickou viskozitou ( r je hustota látky) se pro viskozitu užívá i
název dynamická viskozita. Způsob
měření viskozity je popsán např. v [6].
Význam rovnice
(2,47)
bývá obvykle objasňován
na proudění popsaném rovnicemi
(1,65)
a znázorněném na obr.3, který zde
překreslujeme s poněkud obměněným značením (obr.26). Rychlost
,
s jakou se mění velikost rychlosti
v od desky P1 k desce P2, je úměrná ve-likosti T vektoru smykového napětí
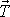působícího na desce P2 (pevná deska P1
musí být držena nejméně silou
,
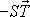kde S je plocha desky). Konstanta úměrnosti mezi
gradientem rychlosti
a velikostí napětí T je rovna převrácené hodnotě viskozity
;
 . |
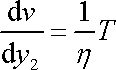V souřadnicové soustavě zvolené na obr.26 je velikost
rychlosti v rovna složce
vektoru rychlosti a společná hodnota
je funkcí pouze souřadnice
,
tedy
.
Velikost napětí T je rovna složce
tenzoru napětí. Poslední rovnici můžeme tedy
přepsat na tvar
 . |
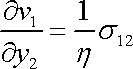(2,47´) |
Přihlédneme-li k rovnici
(1,65)
, dle které
a rovnici
(1,71)
,
dostáváme konečně
 . |
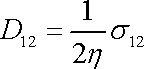(2,48) |
Jelikož při zvoleném způsobu popisu proudění z obr.26
jsou
jedinými nenulovými složkami tenzoru
rychlosti deformace a
jedinými nenulovými složkami tenzoru napětí,
jsou tyto složky také jedinými nenulovými složkami deviátoru tenzoru rychlosti
deformace a deviátoru napětí (srov. úvahy mezi rovnicemi
(2,38)
a
(2,39)
).
Rovnice
(2,47)
je tedy rozšířením rovnice
(2,48)
na obecný případ proudění, kdy
předpokládáme, že vztah typu
(2,48)
platí mezi každou dvojicí složek se
stejnými indexy deviátoru napětí a deviátoru rychlosti deformace.
Dále v této kapitole budeme vynechávat slovo deviátor a indexy značící složky deviátorů, abychom dosáhli jednoduššího vyjadřování. Např. o deviátoru rychlosti deformace budeme mluvit jako o rychlosti deformace a o deviátoru napětí jako o napětí. Rovnici (2,47) pak stručně zapíšeme jako
 , |
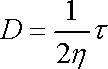(2,49) |
když pro deviátor napětí vzhledem k tomu, že vyjadřuje smykové napětí, užijeme označení t.
Dle rovnice
(1,37)
platí pro
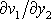z rovnice
(2,47´)
vztah
 , |
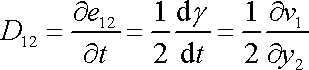(2,50) |
do kterého jsme v druhé rovnici zavedli úhel smyku
(srov. s textem odstavce před definicí
hookovské látky - rov.
(2,6)
). Zavedeme-li dle
(2,50)
do rovnice
(2,49)
časovou
derivaci úhlu smyku, dostaneme její další často užívaný tvar
 . |
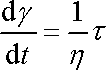(2,51) |
Newtonovská látka (newtonovská kapalina) je látka, pro kterou rychlost deformace je přímo úměrná napětí. Tuto závislost vyjádříme charakteristickou reologickou rovnici
 , |
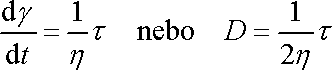(2,52) |
graficky ji vyjádříme přímou úměrností a jako model pro tuto závislost zvolíme píst s připsanou hodnotou viskozity h vystihující odpor pístu proti pohybu jednotkovou rychlostí (viz obr. 27).
Přímá úměrnost mezi rychlostí deformace a
napětím odpovídající rovnici
(2,56)
je v dobrém přiblížení splněna pro
plyn za běžných podmínek, pro vodu, líh, benzen a mnoho dalších
nízkomolekulárních látek. Takové látky lze pokládat za newtonovské a k
vystižení jejích viskózních vlastností stačí udat jedinou materiálovou
konstantu - viskozitu h. Existuje však řada látek, jejichž viskózní chování
tak jednoduše popsat nelze. Ty označujeme jako nenewtonovské a budeme se jimi
zabývat v následující stati.
Nenewtonovské viskozitní chování vykazují např. roztoky a taveniny makromolekulárních látek, jakými jsou laky, asfalty, různé tělní kapaliny apod., různé směsi užívané ve stavebnictví a v potravinářství, ropa, kaly a řada dalších látek.
Na obr.28 je grafem č.1 znázorněna závislost rychlosti
deformace
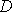na napětí
t pro newtonovskou látku, grafy č. 2, 3 a 4
udávají stejnou závislost pro různé druhy nenewtonovských látek. Rychlost
deformace není pro nenewtonovské látky úměrná napětí - nebo obecněji není
lineární funkcí napětí - , a proto nenewtonovským viskózním látkám říkáme též nelineárně viskózní látky.
Podobně jako chování nelineárně elastických látek (viz grafy na obr.24 a 25) i chování nelineárně viskózních látek je přesně popsáno pouze, známe-li průběh celé křivky
.
(2,53)
Závislost
,
případně inverzní závislost
,
se nazývají rovnicemi toku dané
látky. Pro praktické úkoly je nutno skutečnou rovnici toku i pro nenewto-novské
látky aproximovat jednoduchými funkcemi, jejichž konstanty charakterizují
v daném přiblížení reologické chování skutečné látky. Jednou
z nejznámějších rovnic toku aproximujících chování nenewtonovských látek
je rovnice Ostwaldova -deWaaleova
.
(2,54)
Tato rovnice vystihuje chování látky dvěma konstantami n a
.
Konstanta
je opatřena hvězdičkou, protože pro
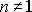má jiný fyzikální rozměr než viskozita h.
Pro
splývá rovnice
(2,54)
s rovnicí
(2,52)
.
Mocninná funkce
(2,54)
zřejmě umožní přijatelně vystihnout chování látek
odpovídající grafům č.2 a 4 na obr.28. Pro graf č.2 bude exponent n rovnice
(2,50)
větší než 1
,
pro graf č.4 bude tento exponent menší než jedna
.
Graf č.3 z obr.28 zřejmě závislostí tvaru
(2,54)
aproximovat nelze. Jak
lze postupovat v takovýchto složitějších případech další poučení o chování
nenewtonovských látek lze získat např. v [22], [23].
Rychlost deformace látky nemusí být pouze funkcí smykového napětí t, ale i doby, po kterou smykové napětí působí. Zvětšuje-li se rychlost deformace s dobou působení stálého smykového napětí, mluvíme o tixotropní látce, zmenšuje-li se rychlost deformace s dobou působení napětí, mluvíme o reopexní látce. Tixotropního chování se snaží výrobci dosáhnout u některých laků; tixotropní lak se po delším působení štětce snáze roztírá, po skončení roztírání nestéká.
|
|
|
|
|
|
|
|
|